C++ және MATLAB тілдерінде үш қабатты жасанды нейрондық торды модельдеу


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 55 бет
Таңдаулыға:
Қaзaқcтaн Pecпубликacының білім жәнe ғылым миниcтpлігі
әл-Фapaби aтындaғы Қaзaқ ұлттық унивepcитeті
Физикa-тeхникaлық фaкультeті
Қaтты дeнe физикacы жәнe бeйcызық физикa кaфeдpacы
«Қopғaуғa жібepілді»
ҚДФжБФ кaфeдpa мeңгepушіcі Пpихoдькo O. Ю.
ДИПЛOМДЫҚ ЖҰМЫC
Тaқыpыбы: «ҮШ ҚАБАТТЫ НЕЙРОНДЫҚ ТОРДЫ C++ ЖӘНЕ MATLAB ОРТАЛАРЫНДА МОДЕЛЬДЕУ»
5B071900 «Радиотехника, электроника және телекоммуникациялар» мaмaндығы бoйыншa
Aлмaты 2015
РЕФЕРАТ
Анықтамалар
Нейрон - құрамында бірнеше кірісі және бір-ақ ғана шығысы бар құрылғы. нейрон клетка денесі және өсімшеден тұрады. Оларды басқаша айтқанда, дендрит пен аксон деп те атайды. Нейронда дендриттер көп, және олар көп таралған, оның көмегімен нейрондар импульстарды көрші клеткалардан жинайды. Ал аксон біреу, ол арқылы нейроннан сигнал өтіп көрші клеткаларға барады
Нейрондық желі - физиологиялық функция атқаратын, жүйке жүйесінде нейрондардың жинақталуы. Нейрондық желі бір-бірімен химиялық және функцианалды байланысқан нейрондық топтар жиынтығынан тұрады. Жасанды нейрондық желі - нейрондық желінің математикалық моделін жасанды нейрондық желі деп атайды. Құрылымды түрде паралельді бөлінетін процессор болып табылады. Ол адам миымен екі аспектіде бірдей:білім және үйрету процесі негізінде жүзеге асады. Оқытылған білімнің сақталуы үшін нейрондық байланыстардың күштері синаптикалық салмақтар қолданады.
Көпқабатты нейрондық тор - көптеген сенсорлық элементтен (кіріс түйін немесе негізгі түйіннен) тұрады, бұл кіріс қабатты құрайды, бір немесе бірнеше жасырын есептеуіші нейрон қабаттарынан және бір шығыс қабатты нейроннан тұрады. Желі бойынша кіріс сигнал тура бағытта, бір қабаттан басқа қабатқа таралады.
Үшқабатты нейрондық желі - кіріс қабаттан, жасырын және шығыс қабаттан тұрады. Кіріс нейрон кіріс мәліметтерді енгізу үшін арналған. Осы қабаттағы нейрондар келесі қабаттағы жасырын қабаттағы элементтермен тығыз байланысқан. Жасырын қабаттағы элементтер шығыс қабаттағы элементтермен тығыз байланысқан.
Перцептрон - бір ғана қабаттан тұратын желі.
Синапс - екі нейрон арасындағы байланыс.
Активация функциясы - нейронның шығысындағы сигналды есептейтін функция болып табылады.
Аксон - жүйке жүйесінің өсімшесі болып табылатын, басқа жүйке жасушаларына импуль таратады. Нейронда аксон біреу ғана.
Дендрит - аксонның химиялық синапсы арқылы ақпарат алатын нейронның таралған өсімшесі
Сигнал - берілген хабарды алып жүретін физикалық процесс.
Тура таралатын желі - нейрондық желідегі ақпаратты тура таратады.
Реккурентті желі - кері байланысы бар нейрондық желілерді айтады.
Үлгіні тану - жүйелерді құрумен байланысы бар, белгілі бір обьектінің қандай да бір классқа анықтау үшін арналған ғылымның бағыты болып табылады. Обьектілердің класстары алдын - ала белгілі болады немесе тапсырманы шешкен кезде анықталады. Үлгіні танудағы үлгі деп отырғанымыз - әр түрлі заттар, құбылыстар, процесстер, сигналдар және т. б.
МАЗМҰНЫ
КІРІСПЕ . . . 5
1 ЖАСАНДЫ НЕЙРОНДЫҚ ЖЕЛІЛЕР ЖӘНЕ ОЛАРДЫҢ ҚҰРЫЛЫМЫ . . . 6
1. 1 Биологиялық нейрондық желі . . . 6
1. 2 Жасанды нейрондық желі . . . 7
2 ЖАСАНДЫ НЕЙРОНДЫҚ ЖЕЛІНІ ҚҰРУ . . . 12
2. 1 Жасанды нейрондық желілердің архитектурасы . . . 12
2. 2 Көпқабатты нейрондық желі құру және негізгі парадигмалары мен ережелері . . . 14
2. 3 Радиалды базистік желілер . . . 25
2. 4 Үлгіні тануға арналған Хопфилд нейрондық желісі . . . 27
3 ЭКСПЕРИМЕНТАЛДЫ ҚҰРЫЛҒЫ . . . 31
3. 1Есептеу жұмыстары жүргізілетін Qt Creater мен Matlab есептеу програмасы . . . 31
4 ТӘЖІРИБЕЛІК НӘТИЖЕСІ . . . 33
ҚОРЫТЫНДЫ . . . 46
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 47
Кіріспе Ақпараттық - коммуникациялық жүйелердің әркелкілігі, қиындықтардың өсуінің үйлесімсіздігі ақпараттық қауіпсіздікті қамтамасыз етуге бағытталған басқа технологияларды, әдістерді, механизмдерді қарастыруды қажет етеді. Сондай бағыттардың бірі - нейрондық желілерді зерттеу. Жасанды нейрондық желілердің теориясы жасанды интеллект саласынан шыққан.Мидың негізін құратын нейрон желісі ақпаратты өңдейтін, жоғары эффективті паралельді, комплексті жүйеге ие. Ол нейрондарды үлгілерді тануға, қиын мәселелерді шешетіндей етіп, жөндей алады. Адам миы кез-келген есептеуіш машиналардан да тез жұмыс істейді және осы факт, ғалымдардың арасында жасанды нейрондық торды ойлап табуына алып келді.
Жасанды нейрондық желі паралельді жұмыс жасайтын көптеген қарапайым элементтерден тұрады. Табиғаттағыдай, нейрондық желі қандай да бір дәрежеде элементтер арасындағы байланысқа ие. Нейрондық желіні нақты функцияны үйретуге қолданады
Жасанды нейрондық желіні ғылым мен техникада қолдану қазіргі кездегі өзекті мәселелердің бірі болып табылады. Мидың коммуникациялық жүйесі болып табылатын әрбір нейрон көптеген қасиетке ие, соның ішіндегі ерекше қасиеттерінің бірі сигналдарды қабылдау, өңдеу және сақтау болып табылады. Нейрондық желілер үлгіні тану, болжау мәселелерінде, басқаруларда, сонымен қатар үлгілерді, иденфикацияны, обьектілердің классификациясын, адам даусын анықтауда қолданылады. Оның себебі, дәстүрлі әдістер көмектесе алмайтын, нейрондық желі кең аумақты әр түрлі ақпараттармен жұмыс жасайды. Жасанды нейрондық желілер биологиялық нейрондық желінің прототипі болғандықтан, ойлау процесін зерттей алады. Жалпы, нейрондық желілердегі ерекше қасиеттердің бірі болып ол - үйрету механизмін қолдану. Нейрондық желіні қолданушы кіріс деректерін енгізеді, содан соң үйрету алгоритмі енгізіледі. Ол автоматты түрде желінің параметрлерін жөндейді. Қазіргі таңда, нейрондық желілер компьютер шеше алмайтын мәселерді шешумен айнлысып жүр.
Зерттеу жұмысының актуалдылығы болып көпқабатты нейрондық желілердің блок - схемасын құру және көпқабатты нейрондық желіні қолдана отырып, үлгіні тану. Сонымен қатар үлгіні тану үшін Хопфилд нейрондық желісін құру.
Дипломдық жұмыста, нейрондық желілердің құрылуының теориялық негіздері, көпқабатты перцептрон, нейрондық желілердің архитектурасы, және нейрондық желілермен байланысқан барлық мәселелер қарастырылған.
Дипломдық жұмыстың мақсаты - Matlab программалау ортасында көпқабатты нейрондық желілердің схемасын Simulink - қосалқы программасында құру. Көпқабатты нейрондық тор моделін құруда активация функцияларын қойып есептеу жұмыстарын жүргізу, алып салыстыру. Осы тұрғыда көпқабатты нейрондық желілер мен Хопфилдтің нейрондық желісін пайдалана отырып, үлгіні тану мәселелерін шешу ұсынылып отыр.
ЖАСАНДЫ НЕЙРОНДЫҚ ЖЕЛІЛЕР ЖӘНЕ ОЛАРДЫҢ ҚҰРЫЛЫМЫ 1. 1Биологиялық нейрондық желі Нейрон дегеніміз - құрамында бірнеше кірісі және бір-ақ ғана шығысы бар желі. Нейрон екі режимде жұмыс істейді: біріншісі үйрету режимі және екіншісі қолдану режимі. Адам миында орташа статистикалық мөлшермен алғанда жиырма миллиард нейрон бар. Бізге белгілі болғандай, нейрон - тор денесі және өсімшеден тұрады. Нейрон - жүйке жүйесінің негізгі функционалды және құрылымдық элементі болып келеді (1. 1 сурет) . Оларды басқаша айтқанда, дендрит пен аксон деп те атайды. Нейронда дендриттер көп, және олар көп таралған, оның көмегімен нейрондар импульстарды көрші торлардан жинайды. Ал аксон біреу, ол арқылы нейроннан сигнал өтіп көрші торларға барады. Ал нейрондық торларда нейрондар бір-бірімен байланысқан, сол арқылы ақпарат таралады. Нейрондардың атқаратын қызметі ақпаратты сақтау және өңдеу, сонымен қатыр өсімшелерді қоректендіріп отыру. Негізінен, орталық жүйке жүйесінде жасушалар бір - бірімен синапс ретінде байланысқан. Синапс - екі нейрон арасындағы байланысқан түйіскен жер. Жалпы кәдімгі нейронның жұмысының негізіне химиялық процесстер кіреді [1] .
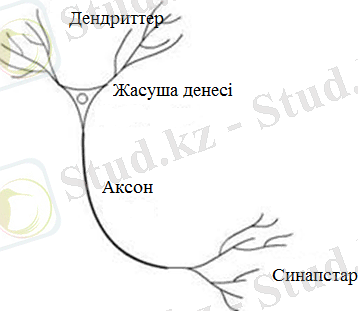
Cурет 1. 1. Биологиялық нейронның моделі
Нейронның беткі жағы таралған өсімшемен жабылған - дендриттермен. Дентриттерге басқа нейрондардың аксонның аяқ жағы жалғасады. Олардың қосылған жерін синапс деп атайды. Синапстық байланыстың арқасында нейрон келіп түскен сигналға жауап қайтара алады және қандай да бір жағдайда өзінің импульсін генерациялай алады. 1. 2 Жасанды нейрондық желі Жасанды нейрон - биологиялық нейронға ұқсас болып келетін, жасанды нейрондық тордың бірлігі болып табылады (сурет 1. 2) . Математикалық тұрғыдан қарасақ, жасанды нейрон анықталу облысында шексіз болатын, бейсызық функция ретінде келетін, жалпы жағдайда кіріс сигналдарының сумматоры түрінде қарастырылады. Әдетте, бұл функция монотонды түрде өседі. Алынған нәтиже шығысына (біреу) жіберіледі. Жасанды нейрондар қандай да бір жолмен қосылып, жасанды нейрондық торды құрады. Әрбір нейрон мидың жүйке торына ұқсас болғандықтан, олардың қазіргі күйі дәл солай сипатталады. Не олар тоқтап калады, не олар қозады. Нейрон синапстық топқа ие - басқа нейронның шығысымен жалғанған кіріс байланыстар, мен шығыс байланысқа ие, бұл арқылы басқа нейронның синапсына сигнал келіп түседі. Әрбір синапс синаптикалық байланыспен немесе салмағымен w сипатталады. Бұл биологиялық нейронның эквивалентті өткізгіштігін көрсетеді [2] . Нейронның қазіргі күйі кірістерінің өлшенілген қосындысы былай анықталады.
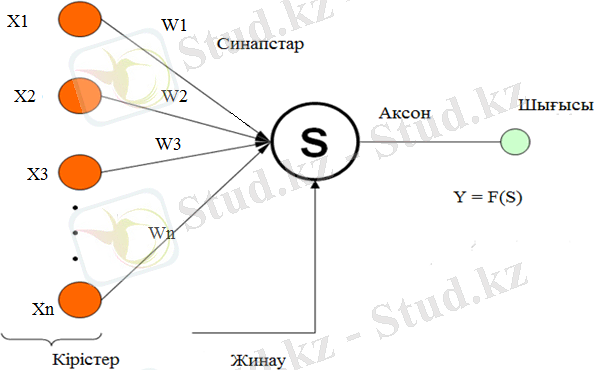 Cурет 1. 2. Жасанды нейрон моделі
Cурет 1. 2. Жасанды нейрон моделі
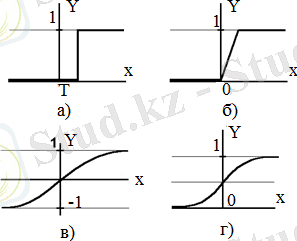
Сурет 1. 3. Aктивация функцияларының түрлері
а) бірлік секірмелі функция; б) сызықты табалдырық (гистерезис) ;
в) сигмоид - гиперболалық тангенс; г) сигмоидты функция
Маккалох пен Питтс жасанды нейрон ретінде бинарлы элементі ұсынды. Бұл формалды нейрон n өлшенілген кіріс сигналдарды есептеп, шығысында бірлік сигнал шығаратын болған. Ары қарай бұл модель толығымен зерттеліп, қазіргі таңда Маккалох пен Питтстің өлшенілген кіріс сигналдары бар бейсызық түрлендіргіш нейроны (сурет 1. 4) деп аталады.
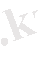
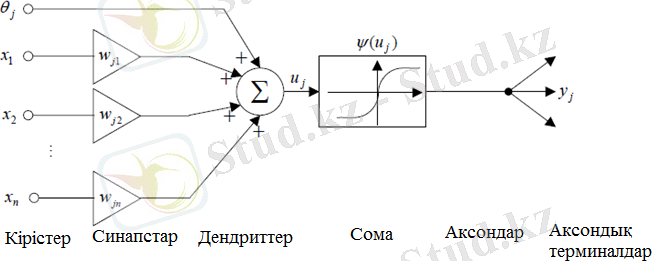
Cурет 1. 4. Маккалох - Питтстің моделі
Төменде нейронның моделі сипатталатын блок схема көрсетілген. Бұл модельде 3 негізгі элементі бар: синапс пен байланыс жинағы салмағымен сипатталатын кіріс сигналдарға көбейтіледі. Сумматор - нейронның синапсына сәйкес өлшенілген кіріс сигналдарды қосады. Активация функциясы -суммарлық сигналдың өлшенілген, сығылған көрінісі. Сондықтан шығыс сигнал шектеулі диапазонға ие, әдетте [0. 1] және [-1. 1] жатады [2] .
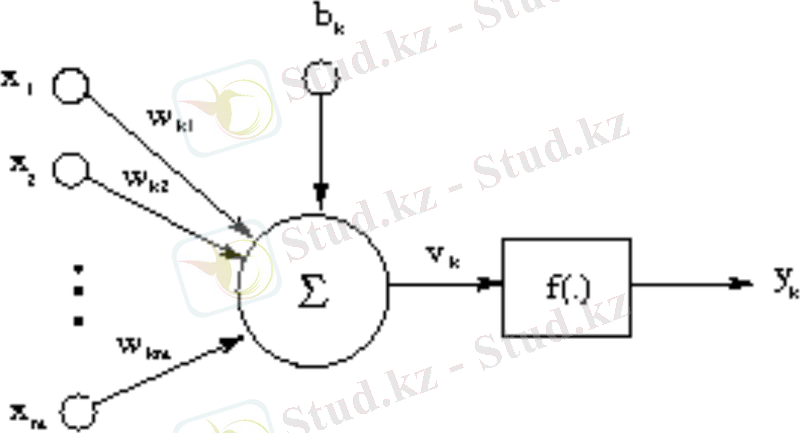
Сурет 1. 5. Нейрон моделі сипатталған қарапайым моделі
Математикалық тұрғыда k-шы нейронның функциялануы былай жазылады:
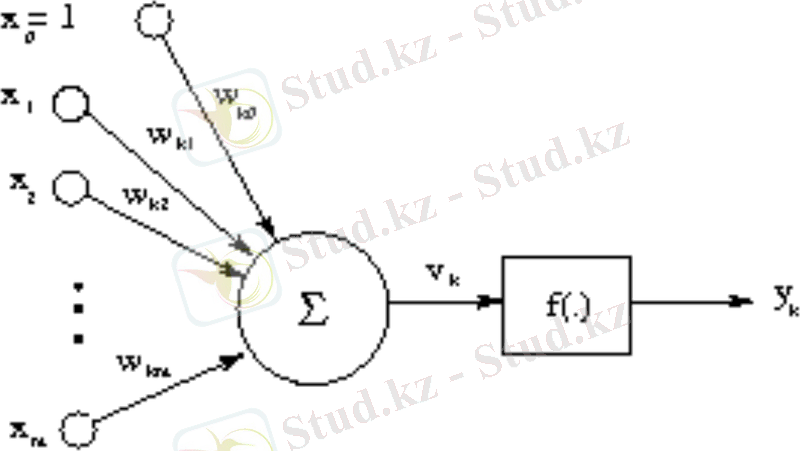
- ЖАСАНДЫ НЕЙРОНДЫҚ ЖЕЛІ ҚҰРУ
2. 1. Жасанды нейрондық желілердің архитектурасы
Нейрондық желі - физиологиялық функция атқаратын, жүйке жүйесінде нейрондардың жинақталуы. Нейрондық желі бір - бірімен химиялық және функцианалды байланысқан нейрондық топтар жиынтығынан тұрады. Нейрондық желі туралы түсінік нейрондық желінің жасанды интеллект туралы түсінік тудырып, математикалық моделін жасауға талпындырды. Нейрондық желінің математикалық моделін жасанды нейрондық желі деп атайды .
Жасанды нейрондық желі - құрылымды түрде паралельді бөлінетін процессор болып табылады. Ол адам миымен екі аспектіде бірдей: білім және үйрету процесі негізінде жүзеге асады. Оқытылған білімнің сақталуы үшін нейрондық байланыстардың күштері синаптикалық салмақтар қолданылады. Жалпы «нейрондық тор» термині ХХ ғасырда пайда бола бастады. Ең бірінші бұл бағыт бойынша жасалған жұмыс Мак-Каллок пен Питтспен байланысты. 1943 жылы математикалық алгоритм негізіндегі нейрондық тордың компьютерлік моделі жобаланды. Олардың болжауынша, нейрондық торды екілік сандарды қолданатын құрылғы деп айтты. Бұл модельді табалдырықтық логика деп атады. Синаптикалық өткізгіштігін сипаттайтын Мак - каллок пен Питтстың нейрондары биологиялық нейронның прототипі болғаннан кейін, нейрондары параметрлерін жөндеу арқылы үйретуге қабілетті. 1949 жылы канадтық физиолог және психолог Хебб мидың нейрондарының байланысы жайлы сөз қозғады. Оның айтуынша, үйрету ең алдымен синаптикалық байланысқа байланысты деп айтты. Хеббтің теориясы өзін-өзі үйретуге негізделген, бұл жерде жүйе ешқандай көмексіз өзінің алдына қойылған тапсырманы орындау үшін тосын үйретілді.
1957 жылы Розенблантпен екі қабатты нейрондық тор негізінде ақпараттың миды қалай қабылдайтына байланысты нейрондық тордың математикалық және компьютерлік моделі ойлап табылды. Розенблант негізгі перцептронды ғана сипаттап қоймай, логикалық қосылуының схемасын да айтып кетті. 1958 жылы адам ойлау қабілетінің процесстерін қайталай алатын электрондық құрылғылар ұсыныла бастады, екі жылдан соң ең бірінші әріптерді тани алатын машина ұсынылды. 1969 жылы Минский мен Пейперттің жұмыстарынан кейін нейрондық торға деген қызығушылық төмендеді. Себебі компьютерлер жоғары есептеушілік қабілетке жеткен кезде нейрондық торды зерттеу тоқтады. Нейронның арасында ақпаратты қабылдап, жіберу 1982 жылы Хопфилд желісі іске асырылды. 2006 жылы бақыланбайтын процедуралар ұсынылған бір немесе бірнеше қабаты бар нейрондық торды үйретудің терең алгоритмі ұсынылды.
Реккурентті желі
Нейрондық желілердің архитектурасы
Хопфилд желісі
Кохонен желісі
Жарыстыр-малы желі
Тура таралу желісі
Бірқабатты
Көпқабатты
Cурет 2. 1. Нейрондық тор архитектурасы
Тура таралу желісі - сигнал тура бағытта ғана тарайды. Сигнал кірісіне кіріп, шығысынан тура бағытта шығады. Кері байланыс болмайды.
Реккурентті нейрондық желі тура таралу желісінен айырмашылғы бар, себебі кері байланысы бар. Мысалы, реккурентті желі бір қабаттан нейроннан тұруы мүмкін және желідегі әрбір шығыс сигнал басқа қабаттардағы нейронның кірісіне жібереді.
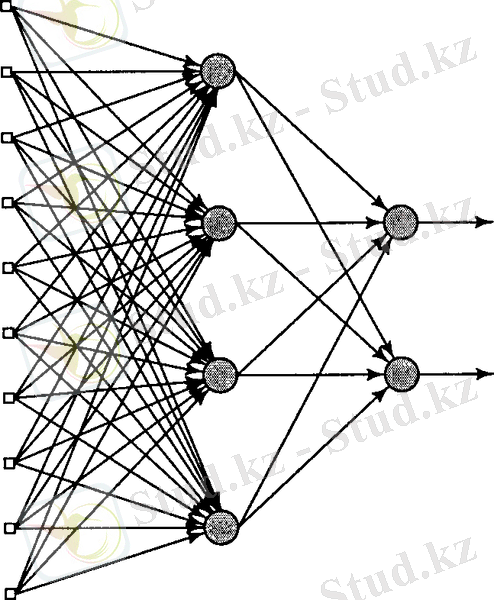
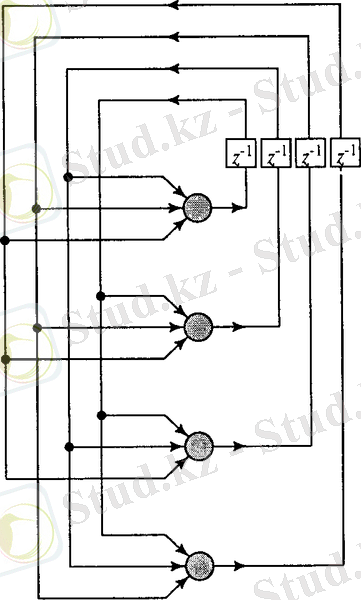
2. 2 Көпқабатты нейрондық желі құру және негізгі парадигмалар мен үйрету ержелері
Көпқабатты желі көптеген сенсорлық элементтен (кіріс түйін немесе негізгі түйіннен) тұрады, бұл кіріс қабатты құрайды, бір немесе бірнеше жасырын есептеуіші нейрон қабаттарынан және бір шығыс қабатты нейроннан тұрады. Желі бойынша кіріс сигнал тура бағытта, бір қабаттан басқа қабатқа таралады. Мұндай желі көпқабатты перцептрон деп аталады [4] . Көпқабатты перцептрон әр түрлі қиын мәселелерді шешу үшін қолданылады. Бұл жердегі мұғаліммен үйретуі белгілі алгоритммен қателердің кері таралу алгоритмі арқылы іске асады. Мұндай алгоритм қателердің коррекциясына негізделген. Қателердің кері таралу әдісімен үйретуі желі бойынша екі кезеңнен тұрады: тура және кері. Тура өткізу кезінде (кіріс вектор) желінің синаптикалық түйініне беріледі, содан соң бір қабаттан екінші қабатқа таралады. Нәтижесінде шығыс сигналдар жиынтығы, генерацияланып, шығысында нәтижесін аламыз. Тура өту кезінде барлық синаптикалық салмақтар фиксацияланады. Ал кері өту кезінде қателер коррекция ережесіне сай барлық синаптикалық салмақтар жөндетіледі. Әсіресе желінің фактылық шығысы керекті жауаптан есептеледі, нәтижесінде қате сигналы пайда болады. Бұл сигнал синаптикалық байланыстардың кері таралуымен таралады. Осы жерден қателердің кері таралуының алгоритмі шығады. Статистикалық мағынада синаптикалық салмақтар бізге керекті шығыс сигналын алу үшін жөндетіледі. Әдебиеттерде қателердің кері таралу алгоритмін кейде кері таралу алгоритмі деп атайды. Көпқабатты перцептронды үйрету процесі осы алгоритм негізінде іске асады .
Жалпы көпқабатты перцептрондар үш айырым белгісіне ие:
1. Әрбір желінің нейроны бейсызық активация функциясына ие. Айтып кететін жағдай, бұл бейсызық функция тегіс болып келеді. Розенбланттын перцептрондарында қолданылатын табалдырық функцияға қарағанда барлық жерде дифференциалданады. Ең танымал функция түрі болып осы шартты қанағаттандыратын сигмоидалдық функция болып табылады. Ол логистикалық функциямен анықталады
\[y_{j}=\frac{1}{1+\exp(-\nu_{j})}\](2. 1)
мұндағы,
2. Желі бір немесе бірнеше қабаттан тұрады жасырын нейрондар, олар желінің кірісіне не шығысына жатпайды. Бұл нейрондар желіге қиын есептерді шешуге үйретеді, нәтижесінде желі кіріс үлгіден(вектордан) маңызды белгілерді өзіне алады.
3. Желі жоғары байланыс дәрежесіне ие, ол орташа синаптикалық байланыспен іске асады. Желінің байланысының деңгейінің өзгерісі салмақ коэфициентін және көптеген синаптикалық байланыстың өзгерісін талап етеді. Үйрету қасиеттерінің жиынтығы көпқабатты перцептронға есептеуіш күш береді. Алайда бұл қасиеттер заманауи білімнің жетіспеушілігінң кесірінен кемшілік болып та келеді. Біріншіден, бейсызық форма және жоғары жоғарғы желілердің байланысы теориялық түрде көпқабатты перцептрондардың анализіне кедергі болып табылады. Екіншіден, жасырын нейрон қабаттарының болуы үйрету процесін қиындатады. Әсіресе үйрету процесінде мына жағдайды ескеру керек, жасырын нейрондарға кіріс сигналдарының қасиеттерін білу шарт. Онда үйрету процесі одан әрі қиындай түседі себебі мүмкін функциясы бар кең аумақта іске асу керек, ал таңдау кіріс үлгілердің альтернативті ортада жасалуы керек [5] .
«Кері таралу» ұғымы 1986 жылдан кейін белсенді түрде қолданыла бастады. Сол жылы ол атақты кітапта жарық көрді. Кері таралу алгоритмінің пайда болуы нейрондық желіде қолданылды. Төмендегі суретте екі жасырын қабатты және бір шығыс қабатты көпқабатты перцептронның архитектуралық графы көрсетілген. Бұл көпқабатты перцептронның сипаттамасына сай толық байланысқан болып келеді. Бұл дегеніміз кез - келген желінің қабатындағы нейрон алдыңғы қабаттаға нейрондармен (түйіндермен) байланысқан. сигнал тура бағытта ғана таралады, солдан оңға қарай, қабаттан қабатқа қарай .
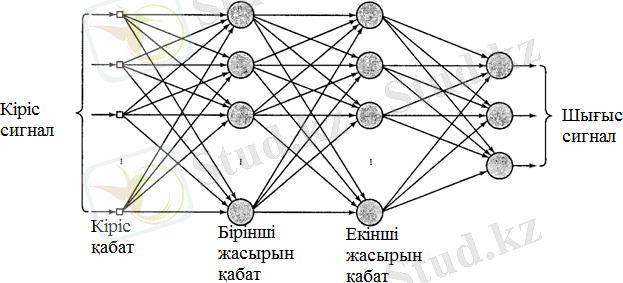
Сурет 2. 3. Екі жасырын қабаты бар көпқабатты перцептронның архитектуралық графы
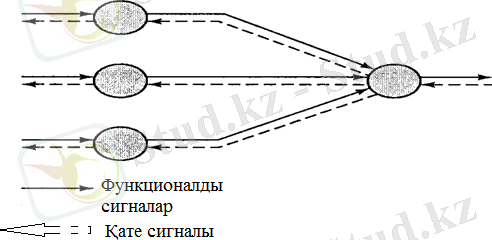
Cурет 2. 4. Көпқабатты перцептронның екі ең негізгі бағыты: функциолналды сигналдың тура таралуы, қате сигналының кері таралуы
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz