Эпитаксиалды процестің динамикасын математикалық пішіндеу

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

ӘЛ - ФАРАБИ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ УНИВЕРСИТЕТІ

МЕХАНИКА - МАТЕМАТИКА ФАКУЛЬТЕТІ

Математикалық және компьютерлік пішіндеу кафедрасы

КЕНДІРБАЕВ М. М.

ЭПИТАКСИАЛДЫ ПРОЦЕСТІҢ ДИНАМИКАСЫН МАТЕМАТИКАЛЫҚ ПІШІНДЕУ

ДИПЛОМДЫҚ ЖҰМЫС

050705 - «Математикалық және компьютерлік пішіндеу» мамандығы

Aлматы 2012

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

ӘЛ - ФАРАБИ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ УНИВЕРСИТЕТІ

« Қорғауға жіберілді»

Кафедра меңгерушісі Мұқанова Б. Г.

ДИПЛОМДЫҚ ЖҰМЫС

Тақырыбы: «ЭПИТАКСИАЛДЫ ПРОЦЕСТІҢ ДИНАМИКАСЫН

МАТЕМАТИКАЛЫҚ ПІШІНДЕУ»

050705 - «Математикалық және компьютерлік пішіндеу» мамандығы

Орындаған 4 курс студенті Кендірбаев М. М.

( қолы, күні)

Ғылыми жетекші Ицкова П. Г.

ф-м. ғ. к., доцент ( қолы, күні)

Норма бақылаушы Ыдырысова Қ. Е.

( қолы, күні)

Кафедра меңгерушісінің Мұқанова Б. Г.

рұқсатымен қорғауға жіберілді ( қолы, күні)

Алматы 2012

РЕФЕРАТ

Жұмыстың мақсаты: эпитаксиальді процестің динамикасын қорытындылау, метрологиялық талдау, тексеру әдістемесі мен метрологиялық қорытынды бағдарламасын жасау.

Жұмыстың міндеті: Газды фазадағы химиялық әдіспен тұндырылу процесінің тізбекті жүзеге асырылуының жуық - аналитикалық және сандық зерттелуі.

Жұмыстың әдістері: Теориядағы дифференциялды теңестірулерді шешудің сапалы әдістері, қарапайым дифференциялды теңестірулерді шешудің сандық әдістері.

Бұл аналитикалық шешім алғашқы шартта көрсетілген сандық есеппен соңғы нәтижелі көріністің яғни шыққан параметрлерді жасауға негізделеді.

Дипломдық жұмыста стационарлы режимдер тұрақтылығының химиялық жолмен газды фазадағы заттардың тұну процестері талданады.

Мұнда нөлдік мөлшердегі математикалық модель немесе пішін қарастырылады. Гидродинамика жылуы яғни суқозғалыс жылуы және оның салмақ ауытқуы ескеріледі. Мұнда күрделі химиялық реакция нәтижесінде пайда болатын күрделі экзотермиялық қоспаның пайда болуы, белгілі бір норманың өлшемдері бар гомоген мен гетерогендік химиялық реакцияның сатысы. Бұл сызықты емес модель 10нан аса өзгермелі мөлшерсіз параметрлерді қамтиды.

Алғашқы нөлдік көрсеткіштіктегі көлемсіз эффективті параметрлер жиынтығына топтастырылады. Бұл сол жердегі динамика я қозғалыс бағытының процесін жеңіл және оңай, жылдам талдауға септігін тигізеді.

Сапалы анализ бифуркациондық диаграммалар мен шағын ауытқу әдісінің көмегімен талданады / / Бифуркациондық // диаграммалар жазықтығындағы « реакцияның жылу эффекті-стационарлы температура ».

Параметрді анықтаушы ретінде қабырға, жұқа қабық, Дамкелер саны және газды фазадағы реакцияның жылу тиімділігі қарастырылады. 3 кесте құрастырылған. Кестеде параметрлердің координаталарға, типтерге, стационарлы жағдайдың тұрақтылығына, эпитаксиалды процестің іске асырылуын болжауға ықпалы бар екенін бейнелейді.

Сапалы талдаудың нәтижесі сандық ғылыми тәжірибелерді жоспарлауға қолданылады. Сандық жағы, Булирша - Штер әдісімен болжам жасау режимі іске асырылған.

Автотербеліс қозуының сипаты, қабырға температурасының ықпалы, жұқа қабықтары, Дамкелер сандары, газды фазадағы гомогенді реакцияның амплитудадағы жиілігі зерттеп танылды.

Қорытынды жұмыстар график түрінде безендірілген және олар 7 кестеде көрсетілген. Температураның стационарлы маңызы бойынша, концентрацияның маңызы бойынша, тербеліс жиілігі бойынша, сөну декременті бойынша, режим ерекшелігі бойынша сандық шешімнің аналитикалық болжамға жуық сәйкестігі анықталды. Автотербеліс процесінің беріктілігі я мықтылығы анықталды.

Алынған нәтижелер (көп параметрлік сызықты емес жүйелерінің динамикасы) ғылыми қызығушылық танытады және нанотехнология дамуы барысында тәжірибе алмасу үшін маңызды. Бұл жұмыстың өзектілігін анықтайды. Осы жұмыста графикалық ақпараттар яғни негізгі сызбаларды қамтитын ақпараттар енгізілген.

Өлшеу құралдары - қайта жаңғыртатын немесе өлшем бірлігін сақтап тұратын (орнатылған қателіктер шегінде) нормаланған метрологиялық сипаттамаларға ие, белгілі уақыт интервал аралығанда өлшеуге арналған техникалық құрал.

Өлшеу құралдарын метролоиялық аттестациялау- оның қасиеттерін зерттеуге негізделіп, бір экземплярда шығарылатын (немесе шет елдерден бір экземплярмен әкелінетін) өлшеу құралдарын қолдануға метрологиялық қызмет көрсету орындарымен заңдастырылған мойындауы.

Өлшеу жүргізу әдістемесі (өлшеу әдістемесі; ӨЖӘ) - өлшеу кезіндегі операциялар мен ережелердің орнатылған жиынтығы, оларды орындау алынған әдіске сәйкес кепілденген дәлдікпен қажетті нәтижелерді алуды қамтамасыз етеді.

Өлшеу құралдарын сенімдеу - өлшеу құралдарының қойылған талаптарға сәйкестігін анықтау және растау мақсатында мемлекеттік қызмет көрсету орындарымен немесе оған уәкіл етілген органдармен орындалатын операциялар жиынтығы.

Техника мен ғылымның барлық саласындағы ғылыми-техникалық прогресс өлшенетін ақпараттың сапасы мен көлемімен тығыз байланысты. Өлшену процесі кезінде алынатын ақпарат, тек жаңа білім алудың ғана көзі емес, технологиялық процестерді басқару үшін де қолданылады. Сондықтан өлшенетін ақпараттың сапасынан нәтижесінде өнімнің сапасы, оны өндіру және қолдану эффективтілігі тәуелді

Қазақстан Республикасында стандарттаудың мемлекеттік жүйесі (СМЖ) енгізілген және жұмыс істейді.

КІРІСПЕ

Техника мен ғылымның барлық саласындағы ғылыми-техникалық прогресс өлшенетін ақпараттың сапасы мен көлемімен тығыз байланысты. Өлшену процесі кезінде алынатын ақпарат, тек жаңа білім алудың ғана көзі емес, технологиялық процестерді басқару үшін де қолданылады. Сондықтан өлшенетін ақпараттың сапасынан нәтижесінде өнімнің сапасы, оны өндіру және қолдану эффективтілігі тәуелді.

« Шығыс болмай, кіріс болмас » - деп айтылған мақалға сүйене отырып бірнеше тұжырымдар я пікірлер келтіруге болады. Адамзат бір істің толық нәтижесіне жету жолында бірнеше шығынға ұшырайды. Егер кәсіпкер өз ісіне шебер болмаса, істің мән - жайын білмесе, оның ашпақ болған өнеркәсібі барып - барып тоқырауға ұшырайды. Бір істі бастамас бұрын техника құрылысының қызметін, атқару функцияларын жақсы білген міндетті. Сол негізде мен сіздерге мына жазған дипломдық жұмыстың алғашқы сөздерін ұсынып отырмын. Мәселен, реактордың өзінің функциясы қандай күшті!? Егер, реактор дұрыс режимде жұмыс істемесе оның түбі техниканың тоқтауына, шығаратын өнім сапа мөлшерінің қысқаруына, келесі жағдайда өнімнің жарамсыз жасалынып шығуына, үшінші жағдайда-мүлдем қирауына алып келіп соқтырады. Сол себепті де жұмыс істеу шарттарын білу тиіс. Сонымен бірге, технологиялық процестің тиімділігін ескере отырып, жұмыс барысының міндеттеріне негіз ретінде жұмыс шарттарының тұрақтылығын дәлелдеген абзал. Химиялық реакторлардың орнықтылығында туындайтын шарасыз мәселелер, яғни проблемалар көптеген ғалымдарды қызықтырды және ол сол жұмыс тұсында өзекті тақырып еді соңғы екі жүз жылдықта. Дәл осы негізде дипломдық жұмыс ұсынылып отыр. Жұмыс талқыланып, санада сұрақтар туындайды. Химиялық реактордың орнықтылығы туралы сұрақтардың қалыптасу жүйесіне қатысты іс шаралар қарастырылады. Кез келген химиялық өнімнің технологиялық схемасының негізгі агрегаты-химиялық реактор. Химиялық реактор-химиялық процестердің өзара я болмаса ішінара өзге затқа айналу құбылыстары, жылу алмасу процестері және масса ауытқуы, салмақ жоғалтуы, салмақ беруі - процестерінің жиынтық құрылғысы.

Дипломдық жұмыс екі негізден құралады. Алғашқы бөлімінде шағын түрде міндеттері туралы жинақты ойлар, өлшемсіз айнымалыларды қолдану туралы мағлұматтар, жеңілдетілген нөлдік математикалық модель баяндалады. Дәл осы жерде жалпыланған таңбалы эффективті жылу коэффиценттерімен және массасының ауытқулары да көрсетілген.

Дипломдық жұмыстың екінші бөлімінде стационарлы жағдайлар қарастырылады және бифуркациондық диаграммалар мысалға келтіріледі.

Үшінші бөлімінде алғашқы Ляпунов әдісі бойынша стационарлық жағдайлардың орнықтылығын талдау әдісі баяндалады.

Төртінші бөлімде осы талдау негізіне сүйене отырып, аз ауытқу әдісімен стационарлық жағдайлардың орнықтылығы мен реактордың эпитакасиалды режимдерінің ықтималдары зерттеледі. Сонымен қоса, автотербеліс қозуының айырмашылығына әсер етуі де зерттелінеді.

CVD - ( ағыл. Chemical vapor deposition) химиялық процес. Ол өте жоғары сапалы, таза материалды шығару үшін қолданылады. Өнеркәсіп я индустрия саласында осы процесті, яғни жұқа қабық жасауда қолданады. Сонымен қоса, ережеге сай CVD жұқа қабық бір немесе бірнеше заттың құрамына ене отырып, реакцияға түседі де, жұқа қабықтың жоғарғы бетіне керекті зат қоспасын өндіріп шығарады. Кей сәттері газ түріндегі заттар да өндіріледі. Алайда ол өте қауіпті және жабық камера ішінде қысылған түрде реакцияға түседі. Оны газ лектері деп те атауға болады.

CVD- процесс әр алуан құрылысты материалдар жасауға негіз: монокристалдар, поликристалдар, эпитаксиалды және аморфты денелер.

Одан: кремний, наномұржалар, Si О ₂ , вольфрам, кремний карбиді, кремний нитриді, титан натриді, көміртегі талшығы, көміртегі наноталшығы, әр алуан диэлектриктері, сонымен қоса, синтетикалық алмаздар алынған материалдар да алынады.

Эпитаксия -монокристалды қабаттардың монокристалды жұқа қабықтардағы қөбею, ұлғаю процестері. Монокристалды жұқа қабықтар эпитаксиалды өсіру я көбейту процесі кезінде бетке ұстар қаймағы секілді негізгі сыртқы пішінді атқарады.

Осы кезде жүріп жатқан кездегі процесті кристализация құбылысы деп те атайды. Нәтиже осыңда бастапқы қалып пішініне ұқсамайтын зат өндіріліп алынады.

1 ЕСЕПТІҢ АЙНЫМАЛЫЛАРЫНЫҢ ӨЛШЕМСІЗ ТҮРДЕ ҚОЙЫЛУЫ

Эпитаксиалды реактордағы идаелды араласу импульсінің, жылуының, реагентінің тасымалдауы қарастырылады. Процесс нөлдік модельде жазылады, химиялық реакцияның газды фазадағы және жоғарғы бетіндегі тұнуының лимиттену сатысы ескеріледі. (Процестің схемасы 1 ші суретте көрсетілген)

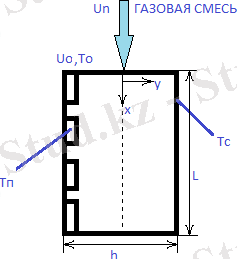Рисунок 1. Схема процесса

Математикалық есеп келесі теңдеулер жүйесі түрінде формуланады.

Қозғалыс теңдеуі:

$\frac{du}{d\tau} = M - 8 \bullet \Pr \bullet u,$ (1. 1)

энергияның теңдеуі:

$\frac{dT}{d\tau} = - 2 \bullet u \bullet \xi \bullet Pe \bullet (T - 1) + \xi \bullet Pe \bullet (1 - u) \bullet (Tn - Tc) + 4 \bullet (Tn - T) + 4 \bullet (Tc - T) + q \bullet Da \bullet (1 - C) \bullet e^{- \frac{\beta}{T}}$ , (1. 2)

Зат тасымалдану теңдеуі:

$\frac{dC}{d\tau} = - 2 \bullet u \bullet \xi \bullet Pe \bullet (C - 1) - \frac{Sh}{Sh + 2} \bullet \left( \left( 4 \bullet Le + 2 \bullet \xi \bullet Pe \bullet (1 - u) \right) \right) \bullet C + Da \bullet (1 - C) \bullet e^{- \frac{\beta}{T}}$ . (1. 3)

Бастапқы шарттары:

τ = 0; T = Tн; C = Cн; u = $u_{н}$ . (1. 4)

Мұндағы:

Т = $\frac{\widehat{Т}}{\overbrace{Т_{0}}}$ - температура; С - концентрация; τ = $\frac{a \bullet t}{h^{2}}$ - уақыт;

u = $\frac{\overbrace{u}}{\overbrace{u_{0}\ }}$ - ұзына бойы жылдамдығы; M = - $\frac{\xi \bullet Pe}{\rho_{0} \bullet u_{0}} \bullet \frac{\partial P}{\partial x}$ - канал ұзындығы бойынша қысымның құлауы; Pr = $\frac{\mu}{\rho \bullet a}$ - Прандтля саны; 𝜉 = $\frac{h}{L}\$ - реактор енінің ұзындығына қатынасы; Pe = $\frac{u_{0} \bullet h}{a}$ - Пекле саны; Tn - жұқа қабық температурасы; Tc - қабырға температурасы; q = $\frac{\overbrace{q}}{Tc \bullet \rho \bullet Cp}$ - газды фазадағы реакцияның жылу эффекті; Da = $\frac{{Ko}_{1} \bullet h^{2}}{a}$ - Дамкелера саны; β = $\frac{E_{1}}{R \bullet T_{0}}$ - газды фазадағы химиялық реакцияның энергия активациясы; ${Sh = Sh}_{1}\exp( - \frac{\beta \bullet \gamma}{T_{n}})$ , γ = $\frac{E_{2}}{E_{1}}$ -жоғарғы бетіндегі тұну химиялық реакция энергия активациясының газды фазадағы химиялық реакция энергия активациясына қатынасы, ${Sh}_{1}$ = $\frac{{Ko}_{2} \bullet h}{D}$ - Шервуд саны; Le = $\frac{D}{a}\$ - Льюис саны,

мұнда

Т - температура; а = $\frac{\lambda}{\rho \bullet Cp}$ - температураөткізу коэффициенті;

ρ - тығыздық; λ - жылуөткізу коэффициенті;

Сp - салыстырмалы жылусыйымдылығы; h - реактордың ені; t - уақыт; L - реактордың ұзындығы; - $\frac{\partial P}{\partial x}$ - реактор ұзындығы бойынша қысымның құлауы ; 𝜇 - динамикалық тұтқырлық; D -диффузия коэффициенті; R - универсал газ тұрақтысы; ${Ko}_{1}$ , $E_{1}$ , q - газды фазадағы химиялық реакцияның экспонента алды көбейткіші, энергия активациясы және жылу эффекті; ${Ko}_{2}$ , $E_{2}$ - химиялық реакция тұнуының экспонента алды көбейткіші, энергия активациясы; н және 0 индекстері бастапқы процеске және реакторға кіруге тиісті; n - жұқа қабыққа; с - қабырғаға.

Процесс үшінші ретті динамикалық жүйе түрінде жазылады. Температура мен концентрацияға қарағанда, жылдамдық ағыны тезірек орнықталғандықтан, бұл жерден демек

$\frac{du}{d\tau}$ =0,

Бұл жерден

M - 8 $\bullet$ Pr $\bullet u_{s}$ =0,

$u_{s} = \frac{M}{8 \bullet \Pr}$ ;

Жылдамдық ағымы анықталғандықтан, ондағы процесс, яғни динамика процесінің екінші реттігімен жазылады. Жүйе (1. 1) - (1. 3) түрін қабылдайды.

$\frac{dT}{d\tau} = - 2 \bullet u_{s} \bullet \xi \bullet Pe \bullet (T - 1) + \xi \bullet Pe \bullet \left( 1 - u_{s} \right) \bullet (Tn - Tc) + 4 \bullet (Tn - T) + 4 \bullet (Tc - T) + q \bullet Da \bullet (1 - C) \bullet e^{- \frac{\beta}{T}}$ ; (1. 5)

$\frac{dC}{d\tau} = - 2 \bullet u_{s} \bullet \xi \bullet Pe \bullet (C - 1) - \frac{Sh}{Sh + 2} \bullet \left( \left( 4 \bullet Le + 2 \bullet \xi \bullet Pe \bullet \left( 1 - u_{s} \right) \right) \right) \bullet C + Da \bullet (1 - C) \bullet e^{- \frac{\beta}{T}}$ ; (1. 6)

Процесс 12 параметрден тұрады: 𝜉, β, Pe, Pr, Da, M, Le, Sh, Tc, Tn, q, u.

Теңдеуді жеңілдету үшін эффективті яғни тиімді коэффициентері бар жалпылауыш модельді қарастырамыз. Эффективті коэффициентерді енгізу үшін теңдеуді келесі түрде жазайық:

$\frac{dT}{d\tau} = - T \bullet \left( 2 \bullet u_{s} \bullet \xi \bullet Pe + 8 \right) + 2 \bullet u_{s} \bullet \xi \bullet Pe - \xi \bullet Pe \bullet \left( 1 - u_{s} \right) \bullet (Tc - Tn) + 4 \bullet (Tc + Tn) + q \bullet Da \bullet (1 - C) \bullet e^{- \frac{\beta}{T}}$ ; (1. 7)

$\frac{dC}{d\tau} = - C \bullet \left( 2 \bullet \xi \bullet Pe \bullet u_{s} + \frac{Sh}{Sh + 2} \bullet \left( 4 \bullet Le + 2 \bullet \xi \bullet Pe \bullet \left( 1 - u_{s} \right) \right) \right) + 2 \bullet u_{s} \bullet \xi \bullet Pe + Da \bullet (1 - C) \bullet e^{- \frac{\beta}{T}}$ . (1. 8)

Келесі эффективті коэффициентерді жалпы түрде жазу үшін енгіземіз:

$$A_{T} = 2 \bullet u_{s} \bullet \xi \bullet Pe + 8;$$

$$B_{T} = 2 \bullet u_{s} \bullet \xi \bullet Pe - \xi \bullet Pe \bullet \left( 1 - u_{s} \right) \bullet (Tc - Tn) + 4 \bullet (Tc + Tn) ;$$

$$A_{C} = 2 \bullet \xi \bullet Pe \bullet u_{s} + \frac{Sh}{Sh + 2} \bullet \left( 4 \bullet Le + 2 \bullet \xi \bullet Pe \bullet \left( 1 - u_{s} \right) \right) ;$$

$B_{C} = 2 \bullet u_{s} \bullet \xi \bullet Pe;$ (1. 9)

$$T_{эф} = \frac{B_{t}}{A_{t}};$$

$$С_{эф} = \frac{B_{c}}{A_{c}};$$

Осы тұста өлшемсіз параметрлер саны кемиді, ал (1. 7) жүйесі - (1. 8) түрін қабылдайды

$\frac{dT}{d\tau} = - A_{T} \bullet \left( T - T_{эф} \right) + q \bullet Da \bullet (1 - C) \bullet e^{- \frac{\beta}{T}}$ ; (1. 10)

$\frac{dC}{d\tau} = - A_{C} \bullet \left( C - C_{эф} \right) + Da \bullet (1 - C) \bullet e^{- \frac{\beta}{T}}$ ; (1. 11)

τ = 0; T = Tн; C = Cн; u = $u_{н}$ ,

где

$Т_{эф}$ , $С_{эф}$ - температура мен концентрацияның эффективті параметрлері.

$А_{С}$ , $А_{Т}$ - параметрлер

Өлшемсіз параметрлер саны жетіге кеміді (1. 2) - (1. 3) (он екі) жүйесіне қарағанда.

2 СТАЦИОНАРЛЫҚ ЖАҒДАЙЫ

Қарастырылып жатқан есеп (1. 10), (1. 11) 8 параметрден тұрады. Координата мен стационарлық жағдай санына параметрлік анализ жүргіземіз.

$\frac{dT}{d\tau} = - A_{T} \bullet \left( T - T_{эф} \right) + q \bullet Da \bullet (1 - C) \bullet e^{- \frac{\beta}{T}}$ $\equiv P(T, C)$ (2. 1)

$\frac{dC}{d\tau} = - A_{C} \bullet \left( C - C_{эф} \right) + Da \bullet (1 - C) \bullet e^{- \frac{\beta}{T}} \equiv Q(T, C)$ (2. 2)

τ = 0; T = Tн; C = Cн.

Дамкелер санының, жұқа қабық және қабырға температурасының, реакция жылу эффектінің процеске ықпалының зерттеу керектігі белгіленген.

Мына параметрлердің тұрақтыланған мәндерінде есептеулер жүргізілді. Le=1, Sh=1, u=0. 125, Pr=1, Pe=0. 3, β=40, 𝜉=0. 1, M=1 .

Жүйенің стационарлық жағдайы мына шарттармен анықталады

$\frac{dT}{d\tau} = 0\ \ \ \ \ \ и\ \ \ \ \ \ \ \frac{dC}{d\tau} = 0$ , (2. 3)

яғни

$P_{1}\left( C_{s}\, {\ T}_{s} \right) = 0$ ,

$P_{2}\left( C_{s}\, {\ T}_{s} \right) = 0$ ,

мұнда s -стационарлық жағдайдың индексі.

Бұдан алатынымыз

$- A_{T} \bullet \left( T_{s} - T_{эф} \right) + q \bullet Da \bullet \left( 1 - C_{s} \right) \bullet e^{- \frac{\beta}{T_{s}}} = 0$ ; (2. 4)

$- A_{C} \bullet \left( C_{s} - C_{еф} \right) + Da \bullet \left( 1 - C_{s} \right) \bullet e^{- \frac{\beta}{T_{s}}} = 0$ ; (2. 5)

(2. 5) теңдеуден $C_{s}$ ті табамыз

... жалғасы

Қанның баяу ағу кезiндегi қанның ұюын математикaлық модeлдeу

Ірі құйындар әдісімен пішіндеу

Кванттық нүктелері бар кеуекті құрылымдар

Наножартылайөткізгіштер

Наноөлшемді кремний карбиді: синтезі, құрылымы, қасиеттері

Пән Жаратылыстанудағы математикалық моделдеу

Экономикада математикалық модельдеуді зерттеу

Микроэлектрониканың даму кезеңдері

Жүйе күйінің функциясы

Орта мектепте информатика пәнін оқытудың негіздері

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс