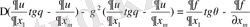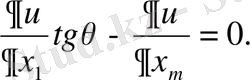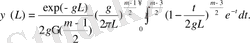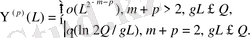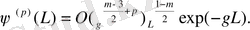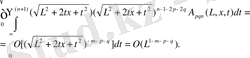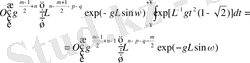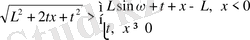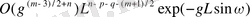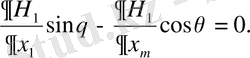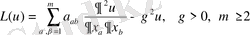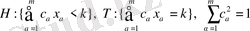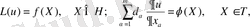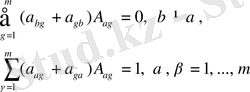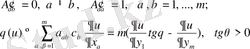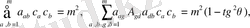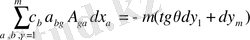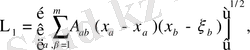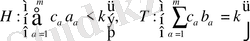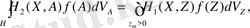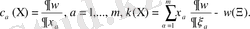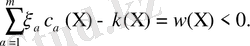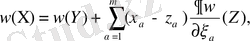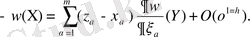Жалпыланған үш өлшемді Мойсил-Теодореско теңдеулер жүйесі үшін Нейман (көлбеу туынды) шекаралық есепті Фредгольм интегралдық теңдеулеріне келтіру


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 33 бет
Таңдаулыға:
ӘЛ-ФАРАБИ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ УНИВЕРСИТЕТІ
МЕХАНИКА-МАТЕМАТИКА ФАКУЛЬТЕТІ
МАГИСТРАТУРА
Іргелі математика кафедрасы
МАГИСТРЛІК ДИССЕРТАЦИЯ
Жалпыланған үш өлшемді Мойсил-Теодереско
теңдеулер жүйесі үшін нетерлік есеп
Орындаушы Султангазиева Ж. Б""2012
/қолы/ /аты-жөні/
Ғылыми жетекшісі ф-м. ғ. к. профессор Токибетов Ж. А. ""2012
/қолы/ /аты-жөні/
Қорғауға жіберілді:
Кафедра меңгерушісі
ф-м. ғ. д. профессор __ Кангужин Б. Е. ""2012
/қолы/ /аты-жөні/
Алматы 2012 ж.
Андатпа
Магистрлік диссертация бірінші ретті эллипстік теңдеулер жүйесіне қойылған шекаралық есеп теориясына арналған. Диссертацияда Риман-Гильберт есебін қарастырылған теңдеулер жүйесінің шешімдерін гармониялық функциялар туындылары арқылы өрнектелген, белгілі көлбеу туындылы есепке әкеліп, оны Булиган-Жиро әдісімен Фредгольм теңдеулер жүйесіне келтірген.
Аннотация
Магистрская диссертация посвяещена для теории краевой задачи эллиптических систем уравнения первого порядка. В диссертации представлена задача Римана-Гильберта решения рассматриваемой системы уравнений с помощью производных гармонических функций, приведен к известной наклонно производной задаче, и методом Булиган-Жиро представлены к системе уравнений Фредгольма.
Summary
Master's thesis is dedicated to the theory of elliptic boundary value problem for systems of equations of first order. The thesis is presented the Rieman-Hilbert solutions of the system of equation with the derivatives of harmonic functions, given the well-known oblique derivative problem and the Bouligan-Zhiro's method presented to the system of Fredgolm equation.
Нормативтік сілтемелер
Магистрлік диссертация Қазақстан Республикасы Ғылым және Білім Министрлігінің, әл-Фараби атындағы Қазақ Ұлттық Университетінің келесідей нормативтік құжаттарына сүйене отырып жазылған:
1. Қазақстан Республикасының "Білім туралы" Заңы (№319-III, 27. 07. 2007)
2. Қазақстан Республикасының "Ғылым туралы" заңы
3. "ҚР МЖМБС 5. 04. 033-2011. Жоғары оқу орнынан кейінгі білім. Магистратура"
4. "Магистрлік диссертацияға қойылатын талаптар" (әл-Фараби атындағы ҚазҰУ-дың Ғылыми Әдістемелік Кеңесінің Мәжілісінде 17. 02. 2012 жылы бекітілген (хаттама №3) )
Мазмұны
Кіріспе . . . … . . . 5
- Көп айнымалыдан тәуелді Гельмгольц теңдеуі үшін қойылған
көлбеу туындылы есепті Фредгольм интегралдық теңдеуіне келтіру…… . . . 8
- Көп айнымалыдан тәуелді еселеуіштері тұрақты жалпы
эллипстік теңдеу үшін қойылған көлбеу туындылы
есепті Фредгольм теңдеуіне келтіру . . . 16
- Көп айнымалыдан тәуелді еселеуіштері айнымалы жалпы
эллипстік теңдеу үшін қойылған көлбеу туындылы
есепті Фредгольм теңдеуіне келтіру . . . 19
- Жалпыланған үш өлшемді кеңістікте Мойсил-Теодереско
теңдеулер жүйесі үшін нетерлік есеп … . . . 22
- Коши-Риман жүйесінің төрт өлшемді
және әртүрлі жалпылаулары . . . 27
- Коши-Риман жүйесінің жалпылауы үшін
бір шекаралық есеп . . . 31
Қорытынды . . . 39
Пайдаланылған әдебиеттер тізімі . . . 40
Кіріспе
Дербес туындылы теңдеулер жүйесінің маңызды бір бөлімі эллипстік теңдеулер мен теңдеулер жүйесі үшін шекаралық есептер теориясы болып табылады. Осындай есептердің ішінен фредгольмдік емес шекаралық есептер деп аталатын есеп қызығушылық танытуда. Бұндай есептерді шешу әдетте сингулярлы интегралдық теңдеулерді зерттеуге келтіріледі. Сонымен қатар, бұндай есептер үшін Фредгольмнің альтернативасы бұзылады.
Қазіргі уақытқа дейін бір өлшемді сингулярлық интегралдық теңдеулердің зерттелуінің арқасында екі тәуелсіз айнымалылы эллипстік теңдеулер үшін шекаралық есептер толығымен зерттелген. Бірақ көпөлшемді тәуелсіз айнымалылы эллипстік теңдеулер үшін шекаралық есептер толық зерттелмеген. Бұл саладағы маңызды сұрақ әлі шешімін таппады, өйткені жеткілікті жалпы әдісі қарастырылмаған.
Шекаралық есептердің арасынан гармониялық функция үшін көлбеу туындылы есеп қазіргі таңда қызығушылық танытып отыр. Бұндай есептер төмендегіше қойылады: Д аймағында Г жатық шекарада
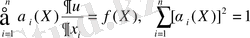
шартты қанағаттандыратын
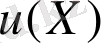 гармоникалық функциясының регулярлығын табу керек. Мұндағы
гармоникалық функциясының регулярлығын табу керек. Мұндағы
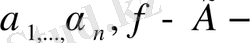 да берілген жатық функциялар. Шекаралық шарттың сол жағындағы
да берілген жатық функциялар. Шекаралық шарттың сол жағындағы
 функциялар Р(Х) векторына бағытталған туындысы
функциялар Р(Х) векторына бағытталған туындысы
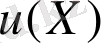 болатын функциялар екені айқын. Егер Р(Х) векторлық өрісі Г кеңістігінің ешқандай нүктесіннен Г жазықтығының жанамасына шықпаса, онда кез келген
болатын функциялар екені айқын. Егер Р(Х) векторлық өрісі Г кеңістігінің ешқандай нүктесіннен Г жазықтығының жанамасына шықпаса, онда кез келген
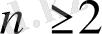 болғанда Фредгольмнің көлбеу туындылы есебі өріс жанамадан Г жазықтығына жіберілсе ғана есеп
болғанда Фредгольмнің көлбеу туындылы есебі өріс жанамадан Г жазықтығына жіберілсе ғана есеп
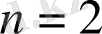 болғанда, аяғына дейін шешілген. Көлбеу туындылы есебін әрқашанда Г-ға сингулярлы интегралдық теңдеулеріне эквивалентті түрде келтіруге болады. Бірақ
болғанда, аяғына дейін шешілген. Көлбеу туындылы есебін әрқашанда Г-ға сингулярлы интегралдық теңдеулеріне эквивалентті түрде келтіруге болады. Бірақ
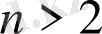 болғанда берілген теңдеуді тек Р(Х) векторлық өрісі ешқандай нүктеде Г жазықтығының жанамасынан шықпаған кезде зерттеуге болады. Р(Х) Г жазықтығының жанамасына шыққан жағдайда интегралдық теңдеулер зерттелмеген.
болғанда берілген теңдеуді тек Р(Х) векторлық өрісі ешқандай нүктеде Г жазықтығының жанамасынан шықпаған кезде зерттеуге болады. Р(Х) Г жазықтығының жанамасына шыққан жағдайда интегралдық теңдеулер зерттелмеген.
Екі тәуелсіз айнымалылы гармоникалық функциясы үшін көлбеу туындылы есебін екі түрлі жолмен шешуге болады: бірі - сингулярлы интегралдық теңдеулерге ықшамдау арқылы, екіншісі - екі тәуелсіз айнымалылы гармоникалық функция қасиеттерін тікелей қолдану арқылы. Екінші жолын тиісті сингулярлы интегралдық теңдеулерді үйрену әдісі ретінде де қолдануға болады. Бұндай қолдану көпөлшемді сингулярлы интергралдық теңдеулер теориясын құру қисынсыз, бірақ Льенардың жұмысында қолданылған екі айнымалылы гармоникалық функция үшін көлбеу туындылы есебін тікелей зерттеу әдісі көп өлшемді жағдайда нәтиже бермейді. Сондықтан көп өлшемді эллиптикалық теңдеулер үшін Фредгольмдік емес шекаралық есептер теориясының негізгі екі мәселесі: а) гармоникалық функция үшін көлбеу туындылы есептерді зерттеу, б) көпөлшемді сингулярлы интегралдық теңдеулердің жалпы теориясын құру. Бұл екі мәселе өзара эквивалентті.
Бұл жұмыста көпөлшемді гармоникалық функциясы үшін көлбеу туындылы есебінің анықталған шама немесе анықталмаған шамаларды үйренуге көп көңіл бөлінген. Берілген есепті конструктивті зерттеу әдісі және осыған қатысты сұрақтар қарастырылған. Сызықты эллиптикалық теңдеулер теориясының негізгі фактлерді және де қосымша мәліметтер келтірген. Ең алдымен үш өлшемді жағдай қарастырылған, ал көпөлшемді жалпылауының толық дәлелі берілмеген. Екінші ретті теңдеулер үшін әр түрлі шекаралық есептер және сингулярлы интегралдық теңдеулерге келтіру әдістері қарастырылған.
Сонымен қатар екінші бөлім көлбеу туындылы есепке арналған. Есеп Фредгольмдік болған жағдайда эквивалентті Фредгольм теңдеуіне көлбеу туындылы есебін ықшамдау -Булигано-Жиро әдісі берілген. Жазық облыс шекарасына жанаманы диференциялдау бағытына шығу туралы нәтижеге нақты мысал келтірілген. Және де фредгольмдігі бұзылған жағдайда есептердің жауабын іздеуге Булигано-Жиро әдісін қолдануға болатынын көрсетілген. Енді есеп Фредгольм теңдеуіне эквивалент емес, сондықтан Фредгольм теңдеуінен шықпайтын сұрақтың жауабын түбегейлі қарауды талап етеді.
1. Көп айнымалыдан тәуелді Гельмгольц теңдеуі үшін
қойылған көлбеу туындылы есепті Фредгольм
интегралдық теңдеуіне келтіру
Егер
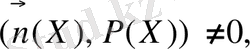
шарты орындалса, онда көлбеу туындылы есеп Фредгольмнің альтернативасы орындалатын сингулярлық интегралдық теңдеулерге келтіріледі. Олай болса, расында да бұл есепті Фредгольм теңдеуіне келтіруге бола ма деген сұрақ туындайды. Бұл сұраққа жауап беру үшін қосымша есептер қарастыру керек. Мына есептен бастайық:
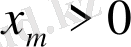 жарты кеңістігінде шексіздікте 0-ге тең,
жарты кеңістігінде шексіздікте 0-ге тең,
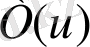 туындысы
туындысы
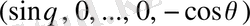
бағыты бойынша мына шартты қанағаттандыратын
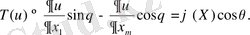 (1)
(1)
және
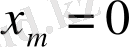 гипержазықтықтың барлық нүктесінде табыл
гипержазықтықтың барлық нүктесінде табыл
гипержазықтықтың барлық нүктесінде табылатын
(2)
теңдеуінің регуляр шешімін табу.
Басында
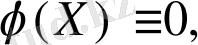 жағдайын қарастырамыз,
жағдайын қарастырамыз,
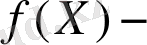 үзіліссіз
үзіліссіз
дифференциялданатын функция. Себебі
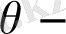 тұрақты шама, (1), (2) есептерінің жауаптары
тұрақты шама, (1), (2) есептерінің жауаптары
теңдеуін қанағаттандырса,
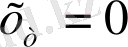 болғанда, келесі теңдеуді аламыз
болғанда, келесі теңдеуді аламыз
Бұдан
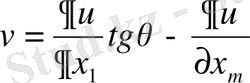 функциясы
функциясы
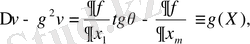
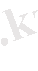 теңдеуінің шешімі.
теңдеуінің шешімі.
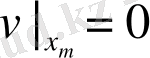 (3)
(3)
Осы есеп үшін Грин функциясын құрайық. L- Х және А нүктелері арасындағы арақашықтық болсын. (2) теңдеуінің
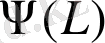 негізгі іргелі шешімі мына формуламен беріледі:
негізгі іргелі шешімі мына формуламен беріледі:
Бұл іргелі шешім және L бойынша төмендегі қатынасты қанағаттандыратын р туынды реті.
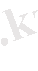 Егер
Егер
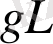 өлшемі
өлшемі
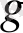 -дан тәуелсіз кейбір оң өлшеммен төменнен шенелсе, онда келесі теңдікті аламыз:
-дан тәуелсіз кейбір оң өлшеммен төменнен шенелсе, онда келесі теңдікті аламыз:
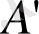 нүктесі арқылы А нүктесіне симметриялы
нүктесі арқылы А нүктесіне симметриялы
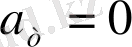 жазықтықтарына біршама нүктені белгілейміз. (3) есебі үшін Грин функциясы
жазықтықтарына біршама нүктені белгілейміз. (3) есебі үшін Грин функциясы
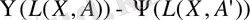 өрнегі арқылы берілетіні анық. Сондықтан төмендегі өрнекті табамыз:
өрнегі арқылы берілетіні анық. Сондықтан төмендегі өрнекті табамыз:
(4)
Мұндағы
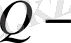 жарты жазықтық
жарты жазықтық
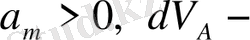 осы жарты жазықтықтың көлем элементі.
осы жарты жазықтықтың көлем элементі.
(4) өрнегіне төмендегі қатынас арқылы жаңа айнымалы енгіземіз:
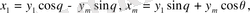
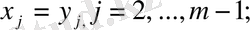
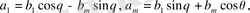
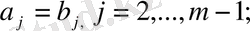

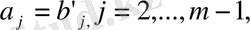
Бұдан алатынымыз:
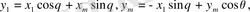
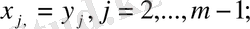
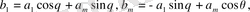
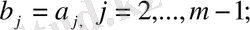
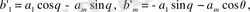
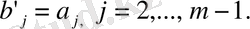
Осы екі топ өрнектерден мынаны аламыз:
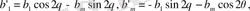
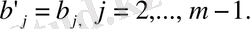
Жаңа айнымалы енгізгеннен кейін (4) формуласын бөліктеп интегралдасақ мынадай түрге келеміз:
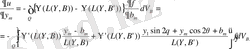 (5)
(5)
 ді табу үшін осы формуланы нәтижесі шексіздікте нөлге ұмтылатындай
ді табу үшін осы формуланы нәтижесі шексіздікте нөлге ұмтылатындай
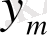 бойынша интегралдау керек.
бойынша интегралдау керек.
 бұрышын және
бұрышын және
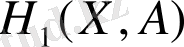 функциясын келесі түрге келтіреміз:
функциясын келесі түрге келтіреміз:
(6)
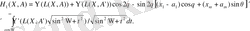 (7)
(7)
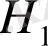 бейнесіндегі бірінші көбейтінді
бейнесіндегі бірінші көбейтінді
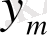 бойынша (5) - те интегралданған бірінші көбейтіндіден алынады және ескі айнымалыға көшеміз. (5) формуладағы екінші интеграл астындағы көбейтінді мына түрге айналады:
бойынша (5) - те интегралданған бірінші көбейтіндіден алынады және ескі айнымалыға көшеміз. (5) формуладағы екінші интеграл астындағы көбейтінді мына түрге айналады:
Теңдіктің екі бөлігіндегі белгілеулерді ауыстырып,
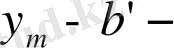 тан
тан
 ке дейін интегралдап мынаны аламыз:
ке дейін интегралдап мынаны аламыз:
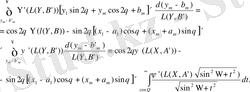
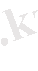 Мұнда мынадай айнымалыны алмастыру жүргізілген:
Мұнда мынадай айнымалыны алмастыру жүргізілген:
Ал төменгі шек интегралдауы (6) бойынша жүзеге асқан.
Өрнегі
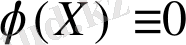 жағдайында (1) және (2) есептердің жауабын береді. Мұндағы
жағдайында (1) және (2) есептердің жауабын береді. Мұндағы
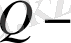 жартыжазықтық
жартыжазықтық
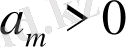 . Алдымен, қарастырылып отырған есептердің Грин функциясы болатын
. Алдымен, қарастырылып отырған есептердің Грин функциясы болатын
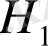 функциясының қасиеттерін зерттейміз. Бұл функция Х функциясы ретінде барлық жерде аналитикалық, тек А нүктесінде және
функциясының қасиеттерін зерттейміз. Бұл функция Х функциясы ретінде барлық жерде аналитикалық, тек А нүктесінде және
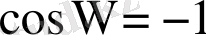 немесе
немесе
 көпбейнесінде аналитикалық емес, себебі
көпбейнесінде аналитикалық емес, себебі
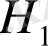 өрнегін өрнектейтін
өрнегін өрнектейтін
 болғанда интеграл келесі түрге ие болады:
болғанда интеграл келесі түрге ие болады:
Ал бұл соңғы интеграл жинақталмайды.
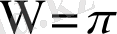 көпбейнелік
көпбейнелік
түрінде беріледі. Егер
анықтауларын енгізсек, онда алдынғы теңдіктен
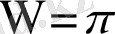 көпбейнелік
көпбейнелік
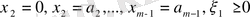 теңдеулерімен беріледі, ал бұл теңдеулер
теңдеулерімен беріледі, ал бұл теңдеулер
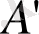 нүктесінен
нүктесінен
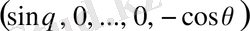 векторының бағыты бойынша шығатын түзу сәулені анықтайтын теңдеулер.
векторының бағыты бойынша шығатын түзу сәулені анықтайтын теңдеулер.
Сол себепті,
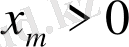 жарты кеңістігінде
жарты кеңістігінде
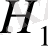 функциясының тек бір ғана
функциясының тек бір ғана
 ерекше нүктесі болады және осы нүктеде
ерекше нүктесі болады және осы нүктеде
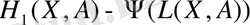 функциясы аналитикалық екені айқын. Демек,
функциясы аналитикалық екені айқын. Демек,
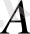 нүктесінде іргелі шешім сияқты қасиетке ие болады.
нүктесінде іргелі шешім сияқты қасиетке ие болады.
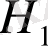 -дің
-дің
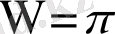 түзуінің сәулесімен қиылысқан кездегі өзгерісін зерттейміз. Ол үшін
түзуінің сәулесімен қиылысқан кездегі өзгерісін зерттейміз. Ол үшін
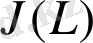 -ді қайта құрайық:
-ді қайта құрайық:
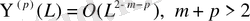 өрнегі жоғарыда көрсетілген.
өрнегі жоғарыда көрсетілген.
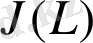 өрнегінен
өрнегінен
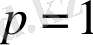 екендігін байқаймыз, сондықтан:
екендігін байқаймыз, сондықтан:
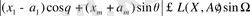 дұрыс теңсіздіктер орындалады. Сол себепті (6) теңдеудің арқасында (7) өрнектегі соңғы қосылғыш
дұрыс теңсіздіктер орындалады. Сол себепті (6) теңдеудің арқасында (7) өрнектегі соңғы қосылғыш
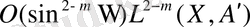 өлшемінің қызметін атқарады.
өлшемінің қызметін атқарады.
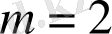 болғанда
болғанда
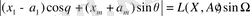 теңдіктері бар болатынын байқаймыз және
теңдіктері бар болатынын байқаймыз және
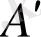 -тан ерекше
-тан ерекше
 сәуле нүктесіне ұмтылған кезде (7) -дегі соңғы қосылғыш
сәуле нүктесіне ұмтылған кезде (7) -дегі соңғы қосылғыш
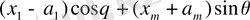 өлшемі таңбасына қатысты қарама-қарсы таңбаларға ие.
өлшемі таңбасына қатысты қарама-қарсы таңбаларға ие.
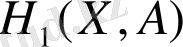 функциясының өзгерісін және оның
функциясының өзгерісін және оның
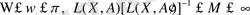 , мұндағы
, мұндағы
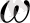 және
және
 шектелген шама, теңсіздіктерін қанағаттандыратын аймақтағы туындысын зерттейміз. Бұл теңсіздік жеке жағдайда
шектелген шама, теңсіздіктерін қанағаттандыратын аймақтағы туындысын зерттейміз. Бұл теңсіздік жеке жағдайда
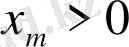 болғанда орындалады. Олай болса,
болғанда орындалады. Олай болса,
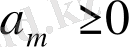 және
және
 бұдан
бұдан
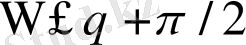 және
және
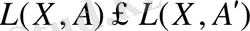 шығыды.
шығыды.
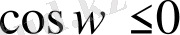 екенін де ескереміз.
екенін де ескереміз.
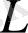 және
және
 айнымалылары бойынша алдыңғы туындылардың өзгерісін зерттейміз.
айнымалылары бойынша алдыңғы туындылардың өзгерісін зерттейміз.
 ны
ны
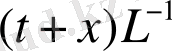 -ге алмастырып,
-ге алмастырып,
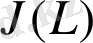 интегралын келесі түрде жазамыз:
интегралын келесі түрде жазамыз:
.
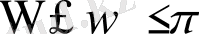 екендігіне қарай
екендігіне қарай
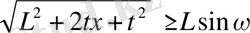 -дан шығатын,
-дан шығатын,
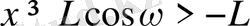 теңсіздігін аламыз, өйткені
теңсіздігін аламыз, өйткені
 Демек, қажетті есептеулерден
Демек, қажетті есептеулерден
аламыз, мұндағы
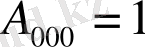 , ал
, ал
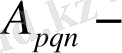
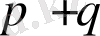 дәрежелі
дәрежелі
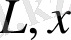 және
және
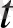 айнымалыларынан алынған біртекті полином. Олай болса,
айнымалыларынан алынған біртекті полином. Олай болса,
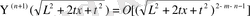 , онда әрбір қосылғыш қосындысы үшін келесі өрнекті аламыз
, онда әрбір қосылғыш қосындысы үшін келесі өрнекті аламыз
Егер
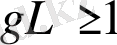 болса, онда басқаш бағалау беруге болады, дәл мынадай:
болса, онда басқаш бағалау беруге болады, дәл мынадай:
(9)
теріс
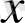 үшін
үшін
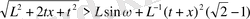
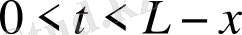 жағдайда бағалауы орындалады, ал
жағдайда бағалауы орындалады, ал
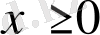 үшін
үшін
 аймағында
аймағында
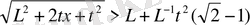 табамыз. (9) өрнегіндегі оң жақ интеграл
табамыз. (9) өрнегіндегі оң жақ интеграл
теңсіздік түрінде орындалатын қисық бойынша алынған (9) өрнегіндегі көпмүшеліктердің қалған бөліктерін интегралдау үшін
бағалауы орынды. Көпмүшелікті осы бөлік бойынша интегралдасақ келесі өрнекті аламыз:
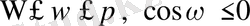 үшін нақты келесі бағалауды аламыз.
үшін нақты келесі бағалауды аламыз.
О символына кіретін
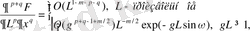
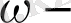 дан тәуелді, бірақ
дан тәуелді, бірақ
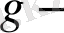 дан тәуелді емес тұрақтылар Енді
дан тәуелді емес тұрақтылар Енді
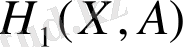 функциясына оралайық. Ол
функциясына оралайық. Ол
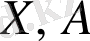 және
және
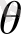 -дан тәуелді. Оны
-дан тәуелді. Оны
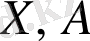 нүктелерінің координаттары бойынша
нүктелерінің координаттары бойынша
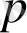 рет,
рет,
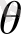 бойынша
бойынша
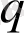 рет дифференциялдаймыз,
рет дифференциялдаймыз,
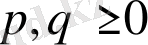 . Жоғарыда өзгертілген бағалаулардан тұжырымның дұрыстығын байқаймыз.
. Жоғарыда өзгертілген бағалаулардан тұжырымның дұрыстығын байқаймыз.
Лемма 1
Егер
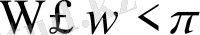 және
және
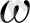 ,
,
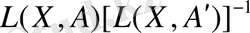 тұрақты өлшеммен жоғарыдан шенелген функцияся
тұрақты өлшеммен жоғарыдан шенелген функцияся
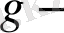 дан тәуелсіз болса, онда
дан тәуелсіз болса, онда
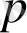 ретті
ретті
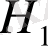 туындысы
туындысы
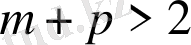 және
және
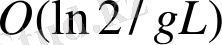 болғанда
болғанда
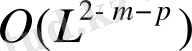 түрінде болады. Егер
түрінде болады. Егер
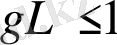 және
және
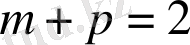 (яғни
(яғни
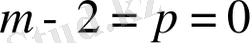 ),
),
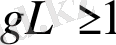 болғанда,
болғанда,
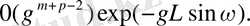
Енді мына өрнекті дәлелдейік:
(10)
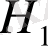 функциясының анықтамасы бойынша келесі өрнекті аламыз:
функциясының анықтамасы бойынша келесі өрнекті аламыз:
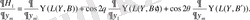
Бұл қатынастан
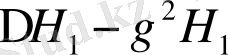 функциясының
функциясының
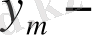 нен тәуелсіздігі,
нен тәуелсіздігі,
 да 0-ге ұмтылатыны және барлық қалған
да 0-ге ұмтылатыны және барлық қалған
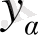 -да шектелгендігі шығады. Осыдан
-да шектелгендігі шығады. Осыдан
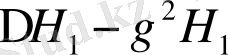 қиыстыруы тек түзудің
қиыстыруы тек түзудің
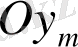 осіне параллел және
осіне параллел және
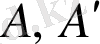 нүктелерінен шығатын сәулесінде нөлден өзгеше болуы мүмкін.
нүктелерінен шығатын сәулесінде нөлден өзгеше болуы мүмкін.
Өйткені, сәуледен
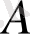 нүктесінен шығатын
нүктесінен шығатын
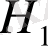 функциясы аналитикалық, бірінші қатынас дәлелденді.
функциясы аналитикалық, бірінші қатынас дәлелденді.
Қажетті есептеулерден келесі өрнекті табамыз.
(11)
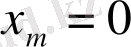 жағдайында
жағдайында
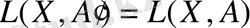 екені айқын, сондықтан
екені айқын, сондықтан
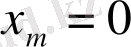 болғанда (11) -ден шығады:
болғанда (11) -ден шығады:
Сонымен, (10) екінші қатынас дәлелденді.
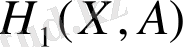 функциясының басқа да қасиеттерін атап өтейік. Егер
функциясының басқа да қасиеттерін атап өтейік. Егер
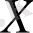 және
және
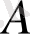 нүктелерінің рөлдерін алмастырсақ, онда
нүктелерінің рөлдерін алмастырсақ, онда
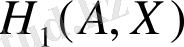 функциясы
функциясы
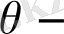 ны -
ны -
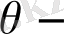 ға өзгертумен бірге (10) -нан шығатын қатынасты қанағаттандырады. Бұл егер
ға өзгертумен бірге (10) -нан шығатын қатынасты қанағаттандырады. Бұл егер
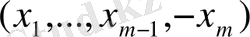 нүктесін
нүктесін
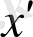 арқылы белгілесек,
арқылы белгілесек,
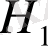 және
және
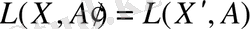 (7) бейнелеуінен тікелей шығады. Ары қарай, егер
(7) бейнелеуінен тікелей шығады. Ары қарай, егер
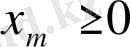 және
және
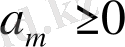 болса, онда
болса, онда
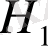 оң.
оң.
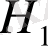
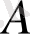 нүктесінің маңайында да оң екені айқын, себебі бұл нүктеде
нүктесінің маңайында да оң екені айқын, себебі бұл нүктеде
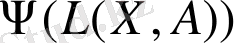
 айналады, ал қалған қосылғыш (7) формуласында өрнектелген
айналады, ал қалған қосылғыш (7) формуласында өрнектелген
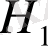 функциясы
функциясы
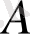 нүктесінде шектелген.
нүктесінде шектелген.
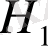 шексіздікте 0-ге айналады. Гипер жазықтықтың
шексіздікте 0-ге айналады. Гипер жазықтықтың
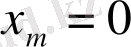 нүктесінде (10) -да орындалған осы гипержазықтықтың бағытына кейбір жанаспайтын жанамалар бойынша
нүктесінде (10) -да орындалған осы гипержазықтықтың бағытына кейбір жанаспайтын жанамалар бойынша
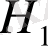 функциясының туындысы нөлге тең. Заремба-Жиро принцпі бойынша
функциясының туындысы нөлге тең. Заремба-Жиро принцпі бойынша
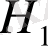 функциясы осы гипержазықтықтың нүктесінде ешқандай теріс минимумға, ешқандай оң максимумға жете алмайды, ал
функциясы осы гипержазықтықтың нүктесінде ешқандай теріс минимумға, ешқандай оң максимумға жете алмайды, ал
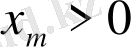 кезінде ол максимум заңы бойынша теріс минимумға жете алмайды. Бұдан кез келген жерде
кезінде ол максимум заңы бойынша теріс минимумға жете алмайды. Бұдан кез келген жерде
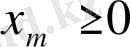 жағдайда
жағдайда
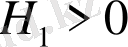 екендігі шығады.
екендігі шығады.
Грин формуласын
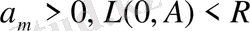 және
және
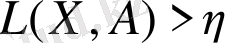 теңсіздіктерімен шектелген аймақта
теңсіздіктерімен шектелген аймақта
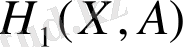 және
және
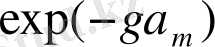 функцияларына қолданамыз. Мұнда О координат басы.
функцияларына қолданамыз. Мұнда О координат басы.
 ді шексіздікке, ал
ді шексіздікке, ал
 ны нөлге ұмтылдырып,
ны нөлге ұмтылдырып,
(12)
Өрнегін аламыз. Мұндағы Г-
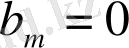 жазықтық, ал
жазықтық, ал
 - осы аймақтың айнымалы нүктесі.
- осы аймақтың айнымалы нүктесі.
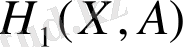 және 1 функцияларына Грин функциясын қолдану нәтижесінде келесі қатынасты аламыз:
және 1 функцияларына Грин функциясын қолдану нәтижесінде келесі қатынасты аламыз:
(13)
Мұндағы жарты
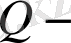 жрты жазықтық
жрты жазықтық
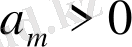 . (
. (
1) және (2) есептерінің шешімі
(14)
түрінде беріледі.
(10) формуласындағы бірінші қатынасқа қарай (14) өрнегі, егер
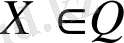 бірінші қосылғышы (8) өрнегінің оң жақ бөлігіне тиісті болса, екінші қосылғыштың оң жағы (2) теңдеуіне сәйкес біртекті теңдеудің шешімі болып табылады. Бұдан (14) өрнегіндегі бірінші қосылғыш (1) шартына тиісті біртекті шекаралық шартын қанағаттандыратын (2) теңдеуінің шешімі. (10) өрнегіне сүйеніп
бірінші қосылғышы (8) өрнегінің оң жақ бөлігіне тиісті болса, екінші қосылғыштың оң жағы (2) теңдеуіне сәйкес біртекті теңдеудің шешімі болып табылады. Бұдан (14) өрнегіндегі бірінші қосылғыш (1) шартына тиісті біртекті шекаралық шартын қанағаттандыратын (2) теңдеуінің шешімі. (10) өрнегіне сүйеніп
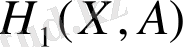 функциясы
функциясы
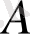 нүктесінде (2) теңдудің іргелі шешімі сияқты маңызды қасиетке ие. (14) өрнегінің екінші қосылғышын қарастырайық:
нүктесінде (2) теңдудің іргелі шешімі сияқты маңызды қасиетке ие. (14) өрнегінің екінші қосылғышын қарастырайық:
Қажетті есептеулерден кейін табатынымыз:
Осы теңдіктің оң жақ бөлігі
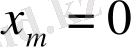 болғанда
болғанда
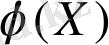 мәні (2) теңдеуіне тиісті біртекті теңдеудің шешімі болып табылады. Сол себепті, (14) өрнегі (1) шартты қанағаттандыратын (2) теңдеудің шешімін береді.
мәні (2) теңдеуіне тиісті біртекті теңдеудің шешімі болып табылады. Сол себепті, (14) өрнегі (1) шартты қанағаттандыратын (2) теңдеудің шешімін береді.
(14) өрнегінен
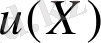 функциясы шексіздікте нөлге айналатынын көрсету ғана қалды.
функциясы шексіздікте нөлге айналатынын көрсету ғана қалды.
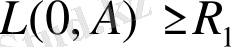 болғанда
болғанда
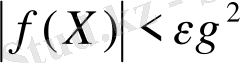 ,
,
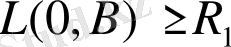 болғанда
болғанда
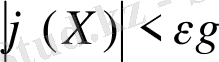 болатындай
болатындай
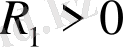 санын аламыз. (14) формуласындағы интегралдарды
санын аламыз. (14) формуласындағы интегралдарды
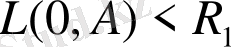 және
және
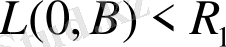 шарларына сәйкесінше және осы шарларға қосымша интегралдарға бөлеміз. (12) және (13) өрнектерінің көмегімен алынған қосымша шарлардың интегралдары абсолют шама бойынша
шарларына сәйкесінше және осы шарларға қосымша интегралдарға бөлеміз. (12) және (13) өрнектерінің көмегімен алынған қосымша шарлардың интегралдары абсолют шама бойынша
 ға артпайды. Шексіздікте
ға артпайды. Шексіздікте
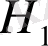 функциясының өзгерісіне қарай шексіздікке ұмтылатын шарлар бойынша алынған интегралдар
функциясының өзгерісіне қарай шексіздікке ұмтылатын шарлар бойынша алынған интегралдар
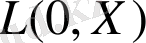 болғанда нөлге ұмтылады. Сол себепті, шарлар бойынша алынған интегралдар қосындысы
болғанда нөлге ұмтылады. Сол себепті, шарлар бойынша алынған интегралдар қосындысы
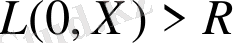 кезінде абсолюттік шама бойынша
кезінде абсолюттік шама бойынша
 нан кем болады. Демек, бұндай
нан кем болады. Демек, бұндай
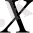 үшін
үшін
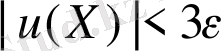 болады, бұл дегеніміз
болады, бұл дегеніміз
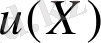 шексіздікте нөлге ұмтылады деген сөз.
шексіздікте нөлге ұмтылады деген сөз.
Егер (1), (2) есептерінің
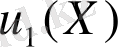 және
және
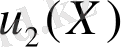 деген екі жауабы болса, онда
деген екі жауабы болса, онда
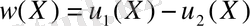 осы жауаптардың айырмашылығы
осы жауаптардың айырмашылығы
қатынасымен қанағаттандырылатын еді және шексіздікте нөлге ұмтылар еді. Берілген қатынастан, максимум және Заремба-Жиро принциптерінен
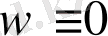 екендігі шығады. Сондықтан (1), (2) есептердің шешімі жалғыз
екендігі шығады. Сондықтан (1), (2) есептердің шешімі жалғыз
және (14) өрнегімен беріледі.
2. Көп айнымалыдан тәуелді еселеуіштері тұрақты жалпы
эллипстік теңдеу үшін қойылған көлбеу туындылы
есепті Фредгольм теңдеуіне келтіру
Жалпы эллипстік оператор қарастырайық:
мұндағы
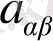 - тұрақты коэффицент,
- тұрақты коэффицент,
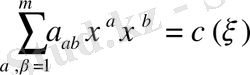 квадраттық формасын оң анықталған деп ұйғарайық.
квадраттық формасын оң анықталған деп ұйғарайық.
 гипержазықтықпен шектелген
гипержазықтықпен шектелген
 жартыкеңістігінде
жартыкеңістігінде
қатынасымен берілетін, төмендегі есепті зерттейік:
мұндағы
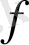 және
және
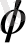 - берілген функциялар,
- берілген функциялар,
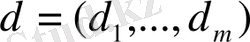 тұрақты векторы
тұрақты векторы
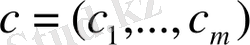 векторымен нөлден өзгеше, тұйық емес бұрыш құрайды. Бұл есепті алдынғы параграфтағы (1) және (2) есептерге келтіруге болады.
векторымен нөлден өзгеше, тұйық емес бұрыш құрайды. Бұл есепті алдынғы параграфтағы (1) және (2) есептерге келтіруге болады.
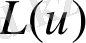 тәуелсіз айнымалылы операторының сызықты алмастыруын
тәуелсіз айнымалылы операторының сызықты алмастыруын
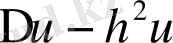 операторына өзгертуге болады. Бұндай өзгертуден соң координат остерін
операторына өзгертуге болады. Бұндай өзгертуден соң координат остерін
 жартыжазықтықтың бейнесіне
жартыжазықтықтың бейнесіне
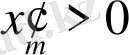 жартыжазықтығы дәл келетіндей бұрылыс жасауға болады. Ары қарай,
жартыжазықтығы дәл келетіндей бұрылыс жасауға болады. Ары қарай,
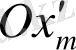 осі бойынша
осі бойынша
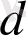 векторының бағыты
векторының бағыты
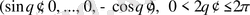 векторының бағытына өзгеретіндей бұруға болады. Нәтижесінде алдынғы параграфтағы (1), (2) есептерге келеміз.
векторының бағытына өзгеретіндей бұруға болады. Нәтижесінде алдынғы параграфтағы (1), (2) есептерге келеміз.
Мұнда тек
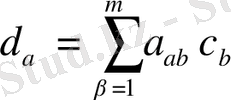 жағдайын ғана қарастырамыз.
жағдайын ғана қарастырамыз.
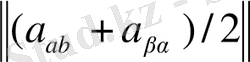 матрицаларын анықтап,
матрицаларын анықтап,
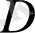 деп белгілейміз.
деп белгілейміз.
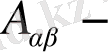 шамасы төмендегі теңдеулер жүйесінен анықталады:
шамасы төмендегі теңдеулер жүйесінен анықталады:
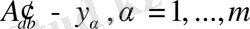 жаңа айнымалға қатысты берілген тұрақты,
жаңа айнымалға қатысты берілген тұрақты,
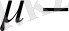 оң тұрақты.
оң тұрақты.
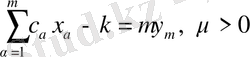
қатынасы орындалатындай
 жаңа тәуелсіз айнымалылар таңдап аламыз.
жаңа тәуелсіз айнымалылар таңдап аламыз.
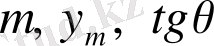 және
және
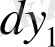 шамаларын анықтау үшін
шамаларын анықтау үшін
тәуелсіз айнымалыларды және оң жағының геометрикалық мағынасын сызықты алмастырғанда теңдеудің сол жағының инварианттылығынан шығатын теңдеу аламыз. Бұл теңдеулерден
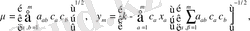
(1)
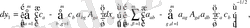
Енді қарастырылып отырған есеп үшін
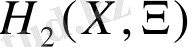 Грин функциясын құрамыз.
Грин функциясын құрамыз.
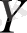 және
және
 - айнымалыларды алмастырғанда сәйкес келетін
- айнымалыларды алмастырғанда сәйкес келетін
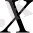 және
және
 нүктелерінің бейнесі болсын.
нүктелерінің бейнесі болсын.
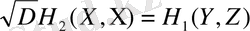 анықтамасы бойынша ұйғарайық, мұндағы
анықтамасы бойынша ұйғарайық, мұндағы
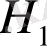 - алдынғы параграфтағы (1), (2) есептеріне жоғарыда құрылған Грин функциясы.
- алдынғы параграфтағы (1), (2) есептеріне жоғарыда құрылған Грин функциясы.
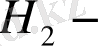 ні айқын түрде көрсету үшін төмендегідей белгілеулер жүргіземіз:
ні айқын түрде көрсету үшін төмендегідей белгілеулер жүргіземіз:
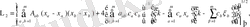
 (2)
(2)

Енді Грин функциясын мына түрде жазуға болады:
(3)
Қарастырылып отырған есептің жауабы
(4)
формуласы бойынша берілетінін көрсетейік. Мұндағы
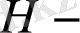 жартыжазықтық,
жартыжазықтық,
 төмендегідей қатынас бойынша берілетін жартыкеңістіктің шекарасы
төмендегідей қатынас бойынша берілетін жартыкеңістіктің шекарасы
ал,
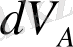 және
және
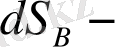 сәйкесінше
сәйкесінше
 және
және
 көлем элементтері. Сызықты айнымалыны алмастыру кезіндегі
көлем элементтері. Сызықты айнымалыны алмастыру кезіндегі
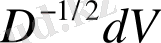 инварианттық шамасы, сондықтан
инварианттық шамасы, сондықтан
мұндағы
 нүктесінің бейнесі,
нүктесінің бейнесі,
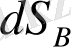 және
және
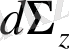 - сәйкесінше
- сәйкесінше
 және
және
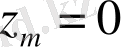 көпбейнеліктерінің көлем элементі. Әртүрлі координаталы әртүрлі цилиндірлік көлемді салыстыра отырып, (1) формуласы бойынша
көпбейнеліктерінің көлем элементі. Әртүрлі координаталы әртүрлі цилиндірлік көлемді салыстыра отырып, (1) формуласы бойынша
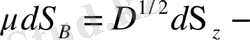 ті аламыз. Бұл келесі өрнектен шығады
ті аламыз. Бұл келесі өрнектен шығады
.
Бұл теңдіктен алдыңғы параграфтағы (1), (2) есептердің шешімдерінің қасиеттерінен (4) өрнегіндегі шекаралық шартты қанағаттандыратын және шексіздікте нөлге ұмтылатын
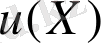 қарастырылып отырған есептің жауабы.
қарастырылып отырған есептің жауабы.
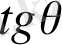 үшін (1) мен (2) -дегі формула
үшін (1) мен (2) -дегі формула
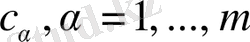 қатысты нөлдік дәреже бойынша біртекті, сонымен бірге
қатысты нөлдік дәреже бойынша біртекті, сонымен бірге
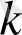 -да біртекті. Сондықтан
-да біртекті. Сондықтан
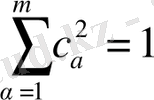 шарты
шарты
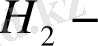 ні өрнектейтін (3) формуласы үшін ешқандай мәні жоқ, бірақ берілген шарт (4) формуласының дұрыстығына қажет, себебі ол шартсыз (4) формуласы дұрыс емес. (4) формуласының көмегімен
ні өрнектейтін (3) формуласы үшін ешқандай мәні жоқ, бірақ берілген шарт (4) формуласының дұрыстығына қажет, себебі ол шартсыз (4) формуласы дұрыс емес. (4) формуласының көмегімен
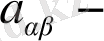 ны
ны
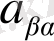 -ға алмастыру (
-ға алмастыру (
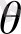 операторын өзгертеді, бірақ
операторын өзгертеді, бірақ
 ді өзгертпейді) барысында Гриннің жаңа функциясы
ді өзгертпейді) барысында Гриннің жаңа функциясы
 функциясына сәйкес келетінін тексеру қиын емес.
функциясына сәйкес келетінін тексеру қиын емес.
3. Көп айнымалыдан тәуелді еселеуіштері айнымалы жалпы
эллипстік теңдеу үшін қойылған көлбеу туындылы
есепті Фредгольм теңдеуіне келтіру
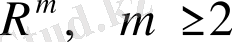 Евклидтік кеңістікте
Евклидтік кеңістікте
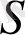 шекаралы, шектелген
шекаралы, шектелген
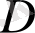 аймағын қарастырамыз. Бұл аймақты кейбір
аймағын қарастырамыз. Бұл аймақты кейбір
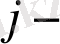 ші координат нүктелері
ші координат нүктелері
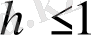 көрсеткішпен Гельдер шартын қанағаттандыратын
көрсеткішпен Гельдер шартын қанағаттандыратын
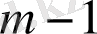 функциясы сияқты өрнектелетіндей
функциясы сияқты өрнектелетіндей
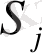 ішкі аймақтың ақырлы сандармен жабуға болады.
ішкі аймақтың ақырлы сандармен жабуға болады.
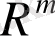 кеңістігінен төртбұрышты координаттар алынады және анықтық үшін
кеңістігінен төртбұрышты координаттар алынады және анықтық үшін
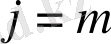 деп ұйғарамыз.
деп ұйғарамыз.
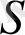 шекарасына бағытталған косинус нормалін
шекарасына бағытталған косинус нормалін
 нүктесінде
нүктесінде
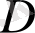 аймағына байланысты
аймағына байланысты
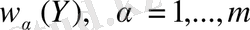 деп белгілейміз.
деп белгілейміз.
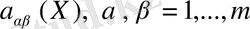 функциясы
функциясы
 тұйық аймағында
тұйық аймағында
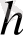 көрсеткішпен Гельдер шартын қанағаттандыратын берілген функция болсын.
көрсеткішпен Гельдер шартын қанағаттандыратын берілген функция болсын.
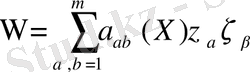 квадраттық формасы
квадраттық формасы
 тұйық аймағында кез келген
тұйық аймағында кез келген
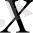 үшін оң анықталған.
үшін оң анықталған.
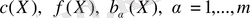 - басқа
- басқа
 аймағында берілген кейбір функциялар, ал
аймағында берілген кейбір функциялар, ал
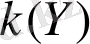 және
және
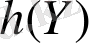
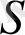 бетінің
бетінің
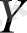 нүктесіндегі үзіліссіз функция.
нүктесіндегі үзіліссіз функция.
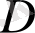 аймағында кез келген екі рет үзіліссіз дифференциялданатын және
аймағында кез келген екі рет үзіліссіз дифференциялданатын және
 аймағында үзіліссіз дифференциялданатын
аймағында үзіліссіз дифференциялданатын
 функциясын
функциясын
(1)
(2)
деп ұйғарайық, мұндағы
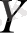
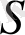 бетінің нүктесі. Келесі есепті зерттейтін боламыз:
бетінің нүктесі. Келесі есепті зерттейтін боламыз:
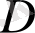 аймағында екі рет дифференциялданатын,
аймағында екі рет дифференциялданатын,
 аймағында үзіліссіз дифференциялданатын
аймағында үзіліссіз дифференциялданатын
(3)
шартын қанағаттандыратын
 функциясын табу керек.
функциясын табу керек.
Бұл есепті зерттеу үшін екі
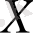 және
және
 нүктелерінің үзіліссіз
нүктелерінің үзіліссіз
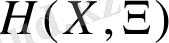 көмекші функциясын құрамыз.
көмекші функциясын құрамыз.
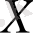 және
және
 нүктелері
нүктелері
 аймағында жатады және әртүрлі .
аймағында жатады және әртүрлі .
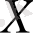 нүктесі
нүктесі
 -ге ұмтылғанда
-ге ұмтылғанда
 нүктесі
нүктесі
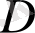 аймағында бекітілген деп есептейміз.
аймағында бекітілген деп есептейміз.
 функциясы
функциясы
 (егер
(егер
 болса, онда басқа қырынан маңызды болуы мүмкін) операторының Грин функциясы сияқты шексіздікке ұмтылады. Егер
болса, онда басқа қырынан маңызды болуы мүмкін) операторының Грин функциясы сияқты шексіздікке ұмтылады. Егер
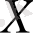 және
және
 сәйкес келмесе, онда
сәйкес келмесе, онда
 екі рет үзіліссіз дифференциялданады және
екі рет үзіліссіз дифференциялданады және
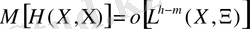
(4)
қатынастыры орындалады, мұндағы
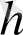 кейбір сандар. Қазір және болашақта
кейбір сандар. Қазір және болашақта
 және
және
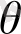 операторлары бірінші нүктенің координаттарына қатысты алынады деп ұйғарамыз. Біз төменде құратын Грин функциясы кейбір
операторлары бірінші нүктенің координаттарына қатысты алынады деп ұйғарамыз. Біз төменде құратын Грин функциясы кейбір
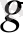 параметріне байланысты болады. Бұл байланыс
параметріне байланысты болады. Бұл байланыс
 функциясының қасиетіне пайдалы.
функциясының қасиетіне пайдалы.
 функциясын құрмас бұрын, кейбір қосымша құрылымдар енгіземіз.
функциясын құрмас бұрын, кейбір қосымша құрылымдар енгіземіз.
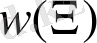 функциясы
функциясы
 аймағында үзіліссіз,
аймағында үзіліссіз,
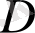 аймағында теріс және
аймағында теріс және
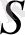 бетінеде нөлге тең функция болсын. Осы функцияның бірінші туындасы бар және кейбір
бетінеде нөлге тең функция болсын. Осы функцияның бірінші туындасы бар және кейбір
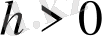 көрсеткішпен Гельдер шартын қанағаттандыратын болсын деп ұйғарамыз.
көрсеткішпен Гельдер шартын қанағаттандыратын болсын деп ұйғарамыз.
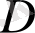 аймағында
аймағында
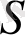 нормалінің бағыты бойынша алынған
нормалінің бағыты бойынша алынған
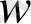 туындысы бар және ол қатаң оң.
туындысы бар және ол қатаң оң.
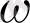 -ға мысалы ретінде келесі есеп жауабын алуға болады:
-ға мысалы ретінде келесі есеп жауабын алуға болады:
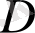 аймағында
аймағында
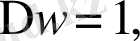 ал
ал
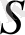 бетінде
бетінде
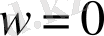 .
.
 тұйық аймағының әрбір нүктесінде
тұйық аймағының әрбір нүктесінде
өрнегін қарастырайық.
Егер
 нүктесінде
нүктесінде
 функциясының барлығы да нөлге ұмтылса, онда
функциясының барлығы да нөлге ұмтылса, онда
(5)
көпбейнелігін
 нүктесінің ассоцияланған көпбейнесі деп атайды.
нүктесінің ассоцияланған көпбейнесі деп атайды.
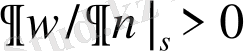 ұйғарымымыз бойынша,
ұйғарымымыз бойынша,
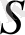 бетіне айтарлықтай жақын
бетіне айтарлықтай жақын
 нүктесі үшін нөлден өзге
нүктесі үшін нөлден өзге
 функциясының ең болмаса біреуіне міндетті. Егер
функциясының ең болмаса біреуіне міндетті. Егер
 болса, онда (5) көпбейнелігі
болса, онда (5) көпбейнелігі
 нүктесіде
нүктесіде
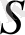 бетіне жанасады, ал егер
бетіне жанасады, ал егер
 нүктесі
нүктесі
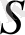 бетінде жатпаса, онда
бетінде жатпаса, онда

 нүктесінен
нүктесінен
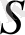 бетінің нүктелер арасындағы қысқа қашықтық.
бетінің нүктелер арасындағы қысқа қашықтық.
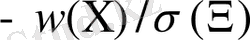 қатынасын төменнен және жоғарыдан шектелгендігін көрсетеміз. Бұл тек кішкене
қатынасын төменнен және жоғарыдан шектелгендігін көрсетеміз. Бұл тек кішкене
 үшін көрсетсек болғаны.
үшін көрсетсек болғаны.
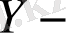
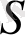 бетінің
бетінің
 нүктесіне жақын нүктесі болсын.
нүктесіне жақын нүктесі болсын.
 түзуінің қиындысы
түзуінің қиындысы
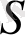 бетінің
бетінің
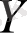 нүктесіне нормалінде жатады және осы кесіндінің
нүктесіне нормалінде жатады және осы кесіндінің
 -ге ең жақын нүктелері
-ге ең жақын нүктелері
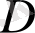 аймағында жатыр. Орта мән туралы теоремадан
аймағында жатыр. Орта мән туралы теоремадан
аламыз

 кесіндісіндегі кейбір нүктелер.
кесіндісіндегі кейбір нүктелер.
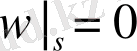 теңдігіне байланысты және осы функцияның бірінші туындысы Гельдер шартын қанағаттандырады. Алдынғы қатынастан
теңдігіне байланысты және осы функцияның бірінші туындысы Гельдер шартын қанағаттандырады. Алдынғы қатынастан
өрнегіне келеміз.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz