Осьтік симметриялы ағыншамен денелердің айнала ағу заңдылықтарын зерттеу


ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ
БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
ӘЛ-ФАРАБИ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ УНИВЕРСИТЕТІ
Физика-техникалық факультеті
Жылуфизика және техникалық физика кафедрасы
Қорғауға жіберілді
Кафедра меңгерушісі, профессор
Бөлегенова С. Ә.
ДИПЛОМДЫҚ ЖҰМЫС
Денелерді оссимметриялық орай ағу кезіндегі заңдылықтарды зерттеу
мамандығы: 5В072300-Техникалық физика
Орындаған 4 курс студенті Құдайберсінова А. Т
(қолы, күні)
Ғылыми жетекші, ф. -м. ғ. к. Исатаев М. С.
(қолы, күні)
Норма бақылаушы:Шортанбаева Ж. Қ
(колы, күні)
Алматы, 2014
РЕФЕРАТ
Дипломдық жұмыс: 57-беттен, кіріспеден, 3-тараудан, 26-суреттен,
56-формуладан, корытынды бөлімнен тұрады.
Жұмыстың негізгі бөлімінде нашар айнала ағатын дененің денеден алыста және соңғысына тікелей жақындағы ізіндегі қозғалысы туралы динамикалық міндетінің шешімдеріне шолу жасалады. Денелердің жіңішке айнала ағуының ерекшеліктері қарастырылады және зерттеу міндеті құрылады.
Жұмыстың мақсаты: Жылуфизика және техникалық физика кафедрасында берілген қондырғыны пайдаланып денелерді оссимметриялық орай ағу кезіндегі заңдылықтарды зерттеу
Алған нәтижелерді бақылау
Денелерді өссимметриялық ағыншамен орай ағу кезіндегі заңдылықтарды зерттеу
ru: Исследование закономерностей при обтекании тел осесимметричной струей
en: Investigation of regularities in the flow around an axisymmetric body jet
ГЛОССАРИЙ
Ағынша - көлденең қимасы аз болатын тесіктен шығатын ағысты айтады.
Жартылай шектелген ағыстар немесе қабырғалық ағыс - бір жағынан қатты бетпен шектелген тұтқұр сұйықтың немесе газдың қозғалысы техникада кең таралған ағыстың түрі.
Турбуленттік ағыс - сұйықтың немесе газдың бөлшектері ретсіз, күрделі траекториясы бойынша хаостық қозғалатын және қозғалған кезде оның температурасы, тығыздығы, қысымы хаостық өзгеріске ұшырайтын ағыс.
Микроманометр - тәжірибелік аэродинамиканың ең басты өлшеулерінің бірі ауа ағынындағы артық мөлшердегі қысымды, яғни атмосфералық қысым мен ағынның статикалық қысымының айырымын өлшейтін, тасымалдауға келетін аспап болып табылады.
Пито түтігі - газ ағынының қысымын өлшейтін құрал.
Сопло - жұмысшы бөліктің алдында жылдамдықтың, тығыздық пен температураның берілген және қима бойынша тұрақты шамаларына ие газ ағынын қамтамасыз ететін аэродинамикалық құбырдың бөлігі.
МАЗМҰНЫ
БЕЛГІЛЕУЛЕР
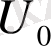 -
ағынның бастапқы жылдамдығы;
-
ағынның бастапқы жылдамдығы;
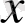 -бойлық координат, м;
-бойлық координат, м;
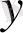 -көлденең координат, м;
-көлденең координат, м;
 -гемпература, К;
-гемпература, К;
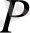 - қысым, Па;
- қысым, Па;
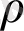 - тығыздық, ;
- тығыздық, ;
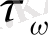 -пластинадағы үйкеліс кернеуі, Па;
-пластинадағы үйкеліс кернеуі, Па;
 -жергілікті кедергі коэфициенті;
-жергілікті кедергі коэфициенті;
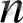 -бөлікгердегі микроманометр көрсеткіші;
-бөлікгердегі микроманометр көрсеткіші;
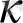 -микроманометрдің иілу коэфициенті, ;
-микроманометрдің иілу коэфициенті, ;
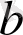 -ағынның бастапқы қалыңдығы;
-ағынның бастапқы қалыңдығы;
 - ағыншаның бастапқы аймағының ұзындығы, м;
- ағыншаның бастапқы аймағының ұзындығы, м;
f -акустикалық әсер жиілігі, Гц;
S-Струхаль саны;
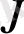 - жіңішке ағыс-науаның турбулентті импульсінің ағыны
- жіңішке ағыс-науаның турбулентті импульсінің ағыны
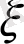 - кедергі коэффициенті
- кедергі коэффициенті
КІРІСПЕ
Сұйықтықтың нашар айнала ағатын дененің ізімен қозғалысы осы қозғалыстың техникада кең таралуына байланысты бұрыннан зерттеушілердің назарын аударуда. Дегенмен, осы сұрақты зерттеуге арналған жұмыстардың көп болуына қарамастан, оның кейбір қырлары әлі де жеткілікті түрде зерттелмеген болып қалып отыр. Жекелей алсақ,
 санының мәні саласындағы турбулентті қозғалысы ең аз және алауды тұрақтандыру, цилиндрдің көлденең айнала ағуы кезіндегі жылу алмасу секілді және т. б. тәжірибеде аса маңызды құбылыстарда негізгі рөл ойнайтын соңғысына тікелей жақындықта дененің ізінде анағұрлым көбірек зерттелген. Тәжірибеде көбіне денелер ені бойынша біртекті емес және соңғы ағынмен, мысалы, еркін жіңішке ағыспен айнала ағады. Көрініп тұрғандай, нашар ағатын формадағы денелердің жіңішке ағысы айтарлықтай қызығушылық туғызатын болса да, әлі зерттелмеген. Осы жұмыс нашар айнала ағатын дененің соңынан соңғысына тікелей жақындықта орталанған турбулентті қозғалыстың заңдылықтарын зерттеуге арналған. Денелердің жалпақ-параллель және осі симметриялы біртекті ағыспен және жалпақ-параллель және осі симметриялы турбулентті жіңішке ағыспен айнала ағуы қарастырылады.
санының мәні саласындағы турбулентті қозғалысы ең аз және алауды тұрақтандыру, цилиндрдің көлденең айнала ағуы кезіндегі жылу алмасу секілді және т. б. тәжірибеде аса маңызды құбылыстарда негізгі рөл ойнайтын соңғысына тікелей жақындықта дененің ізінде анағұрлым көбірек зерттелген. Тәжірибеде көбіне денелер ені бойынша біртекті емес және соңғы ағынмен, мысалы, еркін жіңішке ағыспен айнала ағады. Көрініп тұрғандай, нашар ағатын формадағы денелердің жіңішке ағысы айтарлықтай қызығушылық туғызатын болса да, әлі зерттелмеген. Осы жұмыс нашар айнала ағатын дененің соңынан соңғысына тікелей жақындықта орталанған турбулентті қозғалыстың заңдылықтарын зерттеуге арналған. Денелердің жалпақ-параллель және осі симметриялы біртекті ағыспен және жалпақ-параллель және осі симметриялы турбулентті жіңішке ағыспен айнала ағуы қарастырылады.
Алға қойған міндетке сәйкес жұмыс төрт тарауға бөлінеді.
Бірінші тарауда нашар айнала ағатын дененің денеден алыста және соңғысына тікелей жақындағы ізіндегі қозғалысы туралы динамикалық міндетінің шешімдеріне шолу жасалады. Денелердің жіңішке айнала ағуының ерекшеліктері қарастырылады және зерттеу міндеті құрылады.
Екінші тарауда жалпақ-пареллель және осі симметриялы біртекті ағыста және жалпақ-пареллель және осі симметриялы жіңішке ағыстағы дененің ізіндегі қозғалысты эксперименталды зерттеуге арналған бағдарлар сипаттамасы беріледі. Орташа жылдамдық пен қысымды өлшеу әдістемесі мазмұндалады, сонымен қатар өлшеу нақтылығын бағалау жүргізіледі.
Үшінші тарауда біртекті ағыстағы нашар айнала ағатын дененің ізін эксперименталды зерттеу бойынша нәтижелері қарастырылады және олардың жуық теориялық шешімімен және басқа да тәжірибелі авторлардың мәліметтерімен салыстыруы беріледі.
Жұмыстың негізгі нәтижелері қорытынды бөлімінде жинақталады. Дәл сол бөлімде осы саладағы әрі қарайғы зерттеудің міндеттері көрсетіледі.
1 ШЕКТЕЛМЕГЕН АҒЫНДАҒЫ НАШАР АЙНАЛА АҒАТЫН ДЕНЕ
1. 1 Нашар ағатын дененің айнала ағуы
Доғал кедергінің тұтқыр сығылмайтын сұйықтығының біртекті ағынмен айнала ағуы- нашар ағатын дененің- Рейнольдс санының
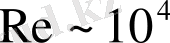 яғни мұндағы
яғни мұндағы
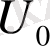 - салмақты қатпарланатын ағын жылдамдығы,
- салмақты қатпарланатын ағын жылдамдығы,
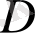 - денеге тән өлшем,
- денеге тән өлшем,
 - сұйықтықтың кинематикалық тұтқырлығы болатын мәндерінің кең саласы үшін көптеген авторлар толық зерттеді және зерделенді. Жекелей алсақ, өте үлкен тәжірибелік қызығушылық тудырып отырған дөңгелек цилиндрдің көлденең айнала ағуы зерттелген. Осі сұйықтықтың қатпарланатын ағыны қозғалысының бағытына перпендикуляр болатын ұзын дөңгелек цилиндр (теориялық түрде-шексіз) айнала ағуын толық қарастырамыз.
- сұйықтықтың кинематикалық тұтқырлығы болатын мәндерінің кең саласы үшін көптеген авторлар толық зерттеді және зерделенді. Жекелей алсақ, өте үлкен тәжірибелік қызығушылық тудырып отырған дөңгелек цилиндрдің көлденең айнала ағуы зерттелген. Осі сұйықтықтың қатпарланатын ағыны қозғалысының бағытына перпендикуляр болатын ұзын дөңгелек цилиндр (теориялық түрде-шексіз) айнала ағуын толық қарастырамыз.
 санның өте кіші мәндерінде (кіші бірліктер), үйкеліс күші инерция күшінен айтарлықтай үлкен болғанда, тұтқырлықтың әсері цилиндрден үлкен қашықтықта сезіледі. Сұйықтық цилиндрді үздіксіз айналып өтеді, ал оның дене артындағы қозғалысы айтарлықтай тежелген.
санның өте кіші мәндерінде (кіші бірліктер), үйкеліс күші инерция күшінен айтарлықтай үлкен болғанда, тұтқырлықтың әсері цилиндрден үлкен қашықтықта сезіледі. Сұйықтық цилиндрді үздіксіз айналып өтеді, ал оның дене артындағы қозғалысы айтарлықтай тежелген.
 саны айтарлықтай аз болатын осындай ағын сұлама қозғалыс деп аталады. Шардың шектеусіз ағынмен біртекті ағынымен айнала ағуы кезіндегі сұлама қозғалысы үшін Навье-Стокс теңсіздіктерінің жуықтап шешуіне алғаш рет Г. Стокc қол жеткізді. Г. Стокс шешімі Навье-Стокс теңсіздіктеріндегі инерциялық мүшелерін есепке алмаған кезде алынды. Дегенмен, шардан бірқатар қашықтықта тұтқыр және инерциялық күштердің әсері өзара салыстырылатын болады. Навье-Стокс теңсіздіктеріндегі инерциялық мүшелерін жартылай есепке алу жолымен Стокс шешімін К. Озин жақсартты. Сұлама қозғалыс шешімдері алынды, сәйкесінше, оны Обербек дөңгелек дискінің айнала ағуы үшін, ал Г. Ламб дөңгелек ұзын цилиндрдің айнала ағуы үшін алды.
саны айтарлықтай аз болатын осындай ағын сұлама қозғалыс деп аталады. Шардың шектеусіз ағынмен біртекті ағынымен айнала ағуы кезіндегі сұлама қозғалысы үшін Навье-Стокс теңсіздіктерінің жуықтап шешуіне алғаш рет Г. Стокc қол жеткізді. Г. Стокс шешімі Навье-Стокс теңсіздіктеріндегі инерциялық мүшелерін есепке алмаған кезде алынды. Дегенмен, шардан бірқатар қашықтықта тұтқыр және инерциялық күштердің әсері өзара салыстырылатын болады. Навье-Стокс теңсіздіктеріндегі инерциялық мүшелерін жартылай есепке алу жолымен Стокс шешімін К. Озин жақсартты. Сұлама қозғалыс шешімдері алынды, сәйкесінше, оны Обербек дөңгелек дискінің айнала ағуы үшін, ал Г. Ламб дөңгелек ұзын цилиндрдің айнала ағуы үшін алды.
 бастап,
бастап,
 санын арттырған кезде, дененің үстіңгі бөлігінде қалыңдықтары ағыс бағытымен арта беретін екі өте нәзік соқпа қабаттар пайда болады. Бұл қабаттар азық аймағындағы кейбір нүктеде дененің беткі қабатынан жұлынып қалады. Жұлып алу құбылысын келесідей тәсілмен түсіндіруге болады. Қоректік, қысымның минимумы нүктесінің соңынан ағыс бойымен төмен қарай цилиндрдің диффуорлы аймағында қысымның артуы жүзеге асады. Бұл бөлікте сұйықтық кіші қысым аймағынан үлкен қысым аймағына қозғалады. Шекарадағы қабаттағы ұзына бойы жылдамдық дененің қабырғасына үйкеліс болғандықтан аз және сұйықтық бөлшектерінің кинетикалық энергиясы өсіп келе жатқан қысымға қарсы шекті азық нүктесіне дейін оның әрі қарайғы қозғалысын қамтамасыз ету үшін жеткіліксіз. Қысымның артуы тоқтап қалуға, ал содан кейін шекарадағы қабаттағы сұйықтықтың кері айналымына да әкеп соқтырады. Кері ағыстың қатпарланған ағынмен кездесуі қатпарлы ағынның цилиндр қабырғасынан жұлынып алынуына әкеліп соғады. Уақыт өте келе жұлқыну нүктесі шекті тұрақты жағдайында қалмайынша дененің алдыңғы бөлігіне қарай қозғалады. Жұлынып алынған құйынды қабаттар бұрылады және дененің артында екі симметриялы тұрақты құйын жасайды. (Сурет 1) .
санын арттырған кезде, дененің үстіңгі бөлігінде қалыңдықтары ағыс бағытымен арта беретін екі өте нәзік соқпа қабаттар пайда болады. Бұл қабаттар азық аймағындағы кейбір нүктеде дененің беткі қабатынан жұлынып қалады. Жұлып алу құбылысын келесідей тәсілмен түсіндіруге болады. Қоректік, қысымның минимумы нүктесінің соңынан ағыс бойымен төмен қарай цилиндрдің диффуорлы аймағында қысымның артуы жүзеге асады. Бұл бөлікте сұйықтық кіші қысым аймағынан үлкен қысым аймағына қозғалады. Шекарадағы қабаттағы ұзына бойы жылдамдық дененің қабырғасына үйкеліс болғандықтан аз және сұйықтық бөлшектерінің кинетикалық энергиясы өсіп келе жатқан қысымға қарсы шекті азық нүктесіне дейін оның әрі қарайғы қозғалысын қамтамасыз ету үшін жеткіліксіз. Қысымның артуы тоқтап қалуға, ал содан кейін шекарадағы қабаттағы сұйықтықтың кері айналымына да әкеп соқтырады. Кері ағыстың қатпарланған ағынмен кездесуі қатпарлы ағынның цилиндр қабырғасынан жұлынып алынуына әкеліп соғады. Уақыт өте келе жұлқыну нүктесі шекті тұрақты жағдайында қалмайынша дененің алдыңғы бөлігіне қарай қозғалады. Жұлынып алынған құйынды қабаттар бұрылады және дененің артында екі симметриялы тұрақты құйын жасайды. (Сурет 1) .
 санының ары қарайғы артуымен құйындар ағын бағытында біртіндеп ұзарады. Құйындардың кернеуі олардағы айнала ағатын беткі қабаттан түсетін құйындылықтың күшеюіне байланысты артады.
санының ары қарайғы артуымен құйындар ағын бағытында біртіндеп ұзарады. Құйындардың кернеуі олардағы айнала ағатын беткі қабаттан түсетін құйындылықтың күшеюіне байланысты артады.

Сурет 1. Кері ағыс, жұлқыныс және құйындардың пайда болуы болған кездегі эллиптикалық цилиндрдің (қысымның арту аймағы) азықтық бөлігінің ұзына бойы ағуы.
Осы құйындардың әрқайсысы дененің артында қатты кері қозғалыс жасайды. Осылайша, дененің артында шашамен сұйықтықтың тұрақты мөлшері айналымда болатын тұйық циркуляциялық ағыс аймағы пайда болады. Осы аймақтың сыртқы шекарасы бойынша қозғалыс саны мен дене соңынан қозғалатын тұйық аймақтың ішінде қозғалатын сұйықтық пен қатпарланатын ағын арасындағы салмақ молекулалық алмасуы жүзеге асырылады. Келесі рет
 санының
санының
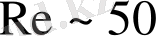 мәнінен бастап артқан кезде айтарлықтай ұзындыққа созылған қозғалмайтын құйындар қисаяды және денеден жұлынып қалады (сурет 2, 3) . Ағынмен тұрақты түрде шайылатын, цилиндрдің екі жағынан кезекпен-кезек жаңа құйындар бөлектенетін ағынның өзіне тән жағдайы дамиды. Осы цилиндрдің артындағы құйындарды ең алғаш рет эксперименталды түрде Г. Бенар зерттеген, одан кейін теориялық түрде зерттеген Т. Карман құйындық жол жасайды.
мәнінен бастап артқан кезде айтарлықтай ұзындыққа созылған қозғалмайтын құйындар қисаяды және денеден жұлынып қалады (сурет 2, 3) . Ағынмен тұрақты түрде шайылатын, цилиндрдің екі жағынан кезекпен-кезек жаңа құйындар бөлектенетін ағынның өзіне тән жағдайы дамиды. Осы цилиндрдің артындағы құйындарды ең алғаш рет эксперименталды түрде Г. Бенар зерттеген, одан кейін теориялық түрде зерттеген Т. Карман құйындық жол жасайды.

Сурет 2. Кіші Рейнольс мәндеріндегі дөңгелек цилиндр айналасындағы ағыс. а)
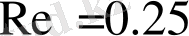
б)
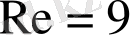
в)
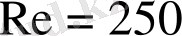

Сурет 3. Жиектері өткір пластинка айналасындағы ағыс.
а)
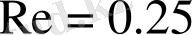
б)
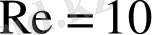
в)
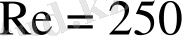
Құйындардың мұндай жағдайы дене артындағы кейбір қашықтыққа дейін сақталады, ал әрі қарай қозғалыс жүйелілігі құйындар диффузиясының салдарынан жоқ болады. Дененің артында сұйықтық салмақты ағындағыдан гөрі ақырындап қозғалатын «із» пайда болады, яғни, дененің артында көлденең қималардың жылдамдық профилінде опырылу бар. Бұл қозғалыс типі
 саны мәндерінің,
саны мәндерінің,
 - дан, шамамен
- дан, шамамен
 дейін кең диапазонда сақталады.
дейін кең диапазонда сақталады.
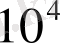
 санынан артық болған кезде құйындар тез басылады, яғни Карманның құйындық жолы дененің артында сақталмайды. Петров пен Штейнберг және басқалардың тәжірибелері көрсеткендей, нашар айнала ағатын дененің артында құйындар жүйелі түрде
санынан артық болған кезде құйындар тез басылады, яғни Карманның құйындық жолы дененің артында сақталмайды. Петров пен Штейнберг және басқалардың тәжірибелері көрсеткендей, нашар айнала ағатын дененің артында құйындар жүйелі түрде
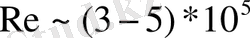 санының мәндеріне дейін жұлынып алынуын жалғастыра береді.
санының мәндеріне дейін жұлынып алынуын жалғастыра береді.
 санының мәндері аймағында, шамамен,
санының мәндері аймағында, шамамен,
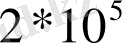 - тен
- тен
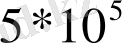 - ке дейін бір қалыпты қоршауы бар денелер үшін денелердің кез -келген кедергісі кезінде коэффиценттің күрт өзгеруі кезінде жасалатын жаңа құбылыс орын алады. Оны алғаш рет шардың айнала ағуы кезінде Констаци мен Эйфель бақылаған болатын. Бұл ламинарлы шекаралық қабаттың жұлынып кету нүктесіне дейін белгілі бір жылдамдықтан өткен кезде турбулентті шекаралық қабатқа өтетініне байланысты. Шекаралық қабаттың турбулизациясы шекаралық қабаттан тыс қозғалатын сұйықтықпен қозғалыс санының күрт алмасуының арқасында шекаралық қабаттағы жылдамдықтың күрт артуына әкеледі. Нәтижесінде, шекаралық қабатта сұйықтықтың кинетикалық энергиясы артады және сұйықтық айтарлықтай қашықтықтағы минимум нүктесінен қысымның тежегіш күшін жеңіп шығуға қабілетті болады. Бұл шекаралық қабаттағы жұлқыну нүктесінің азыққа қарай қозғалуына және дененің қарсыласу коэфицентінің азаюына әкеледі.
- ке дейін бір қалыпты қоршауы бар денелер үшін денелердің кез -келген кедергісі кезінде коэффиценттің күрт өзгеруі кезінде жасалатын жаңа құбылыс орын алады. Оны алғаш рет шардың айнала ағуы кезінде Констаци мен Эйфель бақылаған болатын. Бұл ламинарлы шекаралық қабаттың жұлынып кету нүктесіне дейін белгілі бір жылдамдықтан өткен кезде турбулентті шекаралық қабатқа өтетініне байланысты. Шекаралық қабаттың турбулизациясы шекаралық қабаттан тыс қозғалатын сұйықтықпен қозғалыс санының күрт алмасуының арқасында шекаралық қабаттағы жылдамдықтың күрт артуына әкеледі. Нәтижесінде, шекаралық қабатта сұйықтықтың кинетикалық энергиясы артады және сұйықтық айтарлықтай қашықтықтағы минимум нүктесінен қысымның тежегіш күшін жеңіп шығуға қабілетті болады. Бұл шекаралық қабаттағы жұлқыну нүктесінің азыққа қарай қозғалуына және дененің қарсыласу коэфицентінің азаюына әкеледі.
Жиектері өткір денелердің айнала ағуы жағдайында (мысалы,
 шабуылдау бұрышындағы көлденең айнала ағатын пластинаның) ағыстың сапалы суреті цидиндрдің айнала ағуы кезіндегідей болады. Ағынның жиегі өткір денелерден жұлынып алынуы әрқашан осы жиектерден жүзеге асады, және әрине, осындай денелер үшін айнала ағу дағдарысы таныс емес. Талқыланған ағыс мысалдары жалпақ ағысқа қатысты болды. Осі симметриялы немесе үш өлшемді ағыс кезінде сурет дәл осылайша сақталып қалады. Бір қалыпты қоршауы бар денелерде (шар, эллипсоид және т. б. ) айналып ағу цилиндрдағыдай жүзеге асады, ал жиегі өткір денелерде (көлденең айнала ағатын дискі, шеткі ұзындығы бар пластиналар және т. б. ) - ұзындығы шексіз пластинадағыдай жүреді.
шабуылдау бұрышындағы көлденең айнала ағатын пластинаның) ағыстың сапалы суреті цидиндрдің айнала ағуы кезіндегідей болады. Ағынның жиегі өткір денелерден жұлынып алынуы әрқашан осы жиектерден жүзеге асады, және әрине, осындай денелер үшін айнала ағу дағдарысы таныс емес. Талқыланған ағыс мысалдары жалпақ ағысқа қатысты болды. Осі симметриялы немесе үш өлшемді ағыс кезінде сурет дәл осылайша сақталып қалады. Бір қалыпты қоршауы бар денелерде (шар, эллипсоид және т. б. ) айналып ағу цилиндрдағыдай жүзеге асады, ал жиегі өткір денелерде (көлденең айнала ағатын дискі, шеткі ұзындығы бар пластиналар және т. б. ) - ұзындығы шексіз пластинадағыдай жүреді.
1. 2 Турбулентті ағындағы ағыстың сапалы суреті
Шекаралық қабатпен айнала ағатын дене беткі қабатынан жұлыну арқылы жасалған шырмалған жіңішке ағыстағы сұйықтықтың қозғалысы, ережеге сай, турбулентті. Re санының аз мәндері кезінде де қатты дененің артында ламинарлы құйынды қабат болған кезде, сұйықтықтың қозғалысы денеден бірқатар ара қашықтықта ағыс бойымен төмен қарай турбулентті болады.
 санының мәндері
санының мәндері
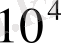 ретімен және одан астам үлкен жиілікпен жүзеге асатын нашар айнала ағатын дененің беткі қабатынан жеке құйындардың жұлқынуы сұйықтықтың өзекті қозғалысының жүйесіз сипатына әкеледі. Іздің бүкіл аймағында бірінші рет қарағанда айтарлықтай күрделі, ретсіз турбулентті қозғалыс орнайды. Мәлім болғандай, жылдамдықтың инерциясыз өлшеуіші (мысалы, термонометр) бұл жағдайда юиіктігі бойынша және ағынның кез-келген нүктесінде қозғалыс жылдамдығының бағытымен үздіксіз хаостық өзгерісті көрсетеді. Нашар айнала ағатын дененің ізіндегі сұйықтықтың турбулентті орталандырылған қозғалысын қиманың екі сипатты аймақтарына бөлуге болады: денеге тікелей жақын жерде және одан алыс қашықтықта (сурет 4) .
ретімен және одан астам үлкен жиілікпен жүзеге асатын нашар айнала ағатын дененің беткі қабатынан жеке құйындардың жұлқынуы сұйықтықтың өзекті қозғалысының жүйесіз сипатына әкеледі. Іздің бүкіл аймағында бірінші рет қарағанда айтарлықтай күрделі, ретсіз турбулентті қозғалыс орнайды. Мәлім болғандай, жылдамдықтың инерциясыз өлшеуіші (мысалы, термонометр) бұл жағдайда юиіктігі бойынша және ағынның кез-келген нүктесінде қозғалыс жылдамдығының бағытымен үздіксіз хаостық өзгерісті көрсетеді. Нашар айнала ағатын дененің ізіндегі сұйықтықтың турбулентті орталандырылған қозғалысын қиманың екі сипатты аймақтарына бөлуге болады: денеге тікелей жақын жерде және одан алыс қашықтықта (сурет 4) .

Сурет 4. Жиектері өткір пластинаның артындағы орталандырылған турбулентті қозғалыстың сызбасы.
Әдебиетте ұзақ уақыт бойы құйындық жолдың орныққан суреті сақталмайтын болғандықтан
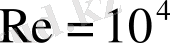 артық болған кезде санының мәндерінде соңғысына тікелей жақындықтағы нашар айнала ағатын дененің ізіндегі сұйықтықтың қозғалысындағы қандай да бір заңдылықтың болмайтыны көрсетіліп келді. Алайда соңғы 10 жылдағы зерттеу нәтижелері көрсетіп отырғандай және т. б. нашар айнала ағатын денедегі іздің тікелей азықтық аймағынды тұйық айналымдық қозғалыстың аймағы орнатылады. Осы тұста ось тұсындағы аймақта сұйықтық дене бағытында, яғни, қатпарлы ағынға қарсы қозғалады. Шектеулі беткі қабаттың жылдамдықтың ұзына бойы компонентасы нөлге тең болғандағы ағысының басқа бөлігінің сыртында сұйықтық салмақты ағын бағытымен қозғалады. Сұйықтықтың тұйықталған айналымдық ағысының аймағы іздің осінде қиылысатын тоқтың
артық болған кезде санының мәндерінде соңғысына тікелей жақындықтағы нашар айнала ағатын дененің ізіндегі сұйықтықтың қозғалысындағы қандай да бір заңдылықтың болмайтыны көрсетіліп келді. Алайда соңғы 10 жылдағы зерттеу нәтижелері көрсетіп отырғандай және т. б. нашар айнала ағатын денедегі іздің тікелей азықтық аймағынды тұйық айналымдық қозғалыстың аймағы орнатылады. Осы тұста ось тұсындағы аймақта сұйықтық дене бағытында, яғни, қатпарлы ағынға қарсы қозғалады. Шектеулі беткі қабаттың жылдамдықтың ұзына бойы компонентасы нөлге тең болғандағы ағысының басқа бөлігінің сыртында сұйықтық салмақты ағын бағытымен қозғалады. Сұйықтықтың тұйықталған айналымдық ағысының аймағы іздің осінде қиылысатын тоқтың
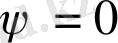 нөлдік сызықтарымен шектелген. Орталандырылған қозғалыс тоғы сызығының осы аймағының ішінде іздің осіне қатысты симметриялы орналасқан тұйықталған қисықтарды көрсетеді. Пласттинананың айнала ағуы сызба түрінде көрсетілген 4 суретінде іздің әр түрлі қималарындағы жылдамдық профильдері көрсетілген. Тұйық айналымдық ағынның аймағы қиылысатын
нөлдік сызықтарымен шектелген. Орталандырылған қозғалыс тоғы сызығының осы аймағының ішінде іздің осіне қатысты симметриялы орналасқан тұйықталған қисықтарды көрсетеді. Пласттинананың айнала ағуы сызба түрінде көрсетілген 4 суретінде іздің әр түрлі қималарындағы жылдамдық профильдері көрсетілген. Тұйық айналымдық ағынның аймағы қиылысатын
 қимасында, нөлдік
қимасында, нөлдік
 жылдамдықтың сызықтарымен шектелген аймағында сұйықтықтың жылдамдықтары қатпарлы ағын қозғалысына қарсы бағытталған. Ағыс бойымен төмен қарай денеден жұлынумен кері ағыс аймағы біртіндеп тарылады және нөлдік жылдамдық сызығының денесінен кейбір ара қашықтықта, сонымен қатар тоқтың нөлдік сызықтары, іздің осінде қабысады. Бұл қимадағы остегі ағынның орталандырылған қозғалысының жылдамдығы нөлге тең (
жылдамдықтың сызықтарымен шектелген аймағында сұйықтықтың жылдамдықтары қатпарлы ағын қозғалысына қарсы бағытталған. Ағыс бойымен төмен қарай денеден жұлынумен кері ағыс аймағы біртіндеп тарылады және нөлдік жылдамдық сызығының денесінен кейбір ара қашықтықта, сонымен қатар тоқтың нөлдік сызықтары, іздің осінде қабысады. Бұл қимадағы остегі ағынның орталандырылған қозғалысының жылдамдығы нөлге тең (
 қима), ал басқа барлық нүктелерде ол ағыс бойымен төмен қарай бағытталған. Айналымдық қозғалыс аймағының сыртқы шекарасы бойынша қозғалыс саны мен салмағының үздіксіз турбулентті алмасуы жүзеге асатынын атап айту қажет. Осылайша, құрамында сұйықтықтың бірқалыпты салмағы ғана бар жабық, ағыстың қалған аймағынан оқшауланған ағын туралы көрініс тек қана орталандырылған қозғалысқа жатады. Денеден әрі қарай алынған кезде із осіндегі жылдамдықтың мәні қатпарлы салмақты ағын жылдамдығана жақындай келе артады. Турбулентті іздің ені де денеден алшақтаған сайын кеңейе түседі. Көптеген эксперименталды және теориялық зерттеулердің нәтижелері көрсетіп отырғандай, денеден алшақ
қима), ал басқа барлық нүктелерде ол ағыс бойымен төмен қарай бағытталған. Айналымдық қозғалыс аймағының сыртқы шекарасы бойынша қозғалыс саны мен салмағының үздіксіз турбулентті алмасуы жүзеге асатынын атап айту қажет. Осылайша, құрамында сұйықтықтың бірқалыпты салмағы ғана бар жабық, ағыстың қалған аймағынан оқшауланған ағын туралы көрініс тек қана орталандырылған қозғалысқа жатады. Денеден әрі қарай алынған кезде із осіндегі жылдамдықтың мәні қатпарлы салмақты ағын жылдамдығана жақындай келе артады. Турбулентті іздің ені де денеден алшақтаған сайын кеңейе түседі. Көптеген эксперименталды және теориялық зерттеулердің нәтижелері көрсетіп отырғандай, денеден алшақ
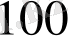 калибр және одан да астам қашықтықтағы ізде жүзеге асырылатын процесстер тұрақталған заңды сипатқа ие болады. Іздің осы аймағындағы сұйықтықтың қозғалысы «автоүлгілі» болады, яғни, геометриялыққа ұқсас денелер үшін іздің өлшемсіз енінің салыстырмалы жылдамдығының таралуы дененің абсолютті өлшемдері мен қатпарланған ағын жылдамдығына тәуелді емес.
калибр және одан да астам қашықтықтағы ізде жүзеге асырылатын процесстер тұрақталған заңды сипатқа ие болады. Іздің осы аймағындағы сұйықтықтың қозғалысы «автоүлгілі» болады, яғни, геометриялыққа ұқсас денелер үшін іздің өлшемсіз енінің салыстырмалы жылдамдығының таралуы дененің абсолютті өлшемдері мен қатпарланған ағын жылдамдығына тәуелді емес.
Л. А. Вулис
 саны мен
саны мен
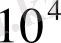 реті және одан да көп мәндерінде орталанған турбулентті қозғалыс тек қана денеден алыста болғанда ғана емес, сонымен қатар денеге тікелей жақындықта да тұрақталған заңды сипатқа ие болады. Дамыған турбулентті қозғалыстың басқа жағдайларындағыдай, нашар айнала ағатын дене жанындағы және іздегі ағыстың бейнесі «автоүлгілі» болады. Геометриялыққа ұқсас денелер үшін ағынның сәйкес нүктелеріндегі жылдамдық векторының бағыты, жылдамдықтардың салыстырмалы профильдері Re санының мәндерінен тәуелсіз бола бастайды. Осы сұрақты құйындардың олқылығының жиілігі туралы белгілі ақпараттарға сүйене отырып, толығырақ қарастырайық. Белгілі болғандай, нашар айнала ағатын дененің ізіндегі қозғалыс жылдамдығының пульсациясы герц тәртібінің жиілігімен жүзеге асырылатын қарапайым ұсақ масштабты турбулентті пульсациялардан және нашар айнала ағатын дененің қабырғаларынан құйындардың олқылығымен шартталған ірі масштабтағы пульсациялардан тұрады. Ірі масштабтағы жылдамдық пульсациялардың тербелісінің амплитудалары қатпарлы салмақты ағын қозғалысының орталандырылған жылдамдығының биіктігінен
реті және одан да көп мәндерінде орталанған турбулентті қозғалыс тек қана денеден алыста болғанда ғана емес, сонымен қатар денеге тікелей жақындықта да тұрақталған заңды сипатқа ие болады. Дамыған турбулентті қозғалыстың басқа жағдайларындағыдай, нашар айнала ағатын дене жанындағы және іздегі ағыстың бейнесі «автоүлгілі» болады. Геометриялыққа ұқсас денелер үшін ағынның сәйкес нүктелеріндегі жылдамдық векторының бағыты, жылдамдықтардың салыстырмалы профильдері Re санының мәндерінен тәуелсіз бола бастайды. Осы сұрақты құйындардың олқылығының жиілігі туралы белгілі ақпараттарға сүйене отырып, толығырақ қарастырайық. Белгілі болғандай, нашар айнала ағатын дененің ізіндегі қозғалыс жылдамдығының пульсациясы герц тәртібінің жиілігімен жүзеге асырылатын қарапайым ұсақ масштабты турбулентті пульсациялардан және нашар айнала ағатын дененің қабырғаларынан құйындардың олқылығымен шартталған ірі масштабтағы пульсациялардан тұрады. Ірі масштабтағы жылдамдық пульсациялардың тербелісінің амплитудалары қатпарлы салмақты ағын қозғалысының орталандырылған жылдамдығының биіктігінен
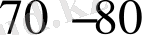 пайыздық мәніне жете алатын жағдайда болған кезде, ұсақ масштабтағы пульсациялардың тербелісінің амплитудалары
пайыздық мәніне жете алатын жағдайда болған кезде, ұсақ масштабтағы пульсациялардың тербелісінің амплитудалары
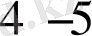 пайыздан аспайды. Ірі масштабты пульсациялардың жиілігі, яғни, құйындардың денеден жұлыну жиілігі, дене өлшемі мен қатпарлы ағын жылдамдығына байланысты айтарлықтай мәндерде (шамамен,
пайыздан аспайды. Ірі масштабты пульсациялардың жиілігі, яғни, құйындардың денеден жұлыну жиілігі, дене өлшемі мен қатпарлы ағын жылдамдығына байланысты айтарлықтай мәндерде (шамамен,
 Гц-тен
Гц-тен
 Гц-ке дейін) өзгере алады. Расында да,
Гц-ке дейін) өзгере алады. Расында да,
 санының мәні аймағында, шамамен
санының мәні аймағында, шамамен
 -тен
-тен
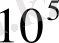 -ке дейін цинлиндр денелер үшін (көлденең айнала ағатын пластина типтес жиектері өткір денелер үшін
-ке дейін цинлиндр денелер үшін (көлденең айнала ағатын пластина типтес жиектері өткір денелер үшін
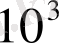 -тен
-тен
 -ға дейін
-ға дейін
 мәндері болғанда) Струхальге тән
мәндері болғанда) Струхальге тән
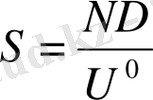 саны тұрақты болып қалатыны тәжірибеден белгілі. Осы тұста
саны тұрақты болып қалатыны тәжірибеден белгілі. Осы тұста
 құйындардың жұлқыну жиілігі
құйындардың жұлқыну жиілігі
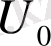 қатпарлы ағысының жылдамдығына тура пропорционал және
қатпарлы ағысының жылдамдығына тура пропорционал және
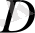 ағатын денеге тән өлшемге кері пропорционал (цилиндр диаметріне, немесе, сәйкесінше, пластина еніне) өзгереді. Осыдан келіп әр түрлі денелер үшін санының мәні тұрақты болғанда құйындардың жұлқыну жиілігі әр түрлі бола алады. Осыны мысалмен түсіндірейік.
ағатын денеге тән өлшемге кері пропорционал (цилиндр диаметріне, немесе, сәйкесінше, пластина еніне) өзгереді. Осыдан келіп әр түрлі денелер үшін санының мәні тұрақты болғанда құйындардың жұлқыну жиілігі әр түрлі бола алады. Осыны мысалмен түсіндірейік.
Көз алдымызға диаметрі см болатын, жылдамдығы м/сек болатын ауа ағынымен айнала ағатын дөңгелек цилиндрді елестетейік. Re мәнінің аймағындағы
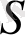 Струхаль критерийі
Струхаль критерийі
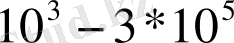 ретімен тұрақты және цилиндр үшін
ретімен тұрақты және цилиндр үшін
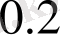 тең. Құйындар қарастырылып отырған цилиндр қабырғаларынан
тең. Құйындар қарастырылып отырған цилиндр қабырғаларынан
 Гц жиілігімен жұлынып аынады. Алайда,
Гц жиілігімен жұлынып аынады. Алайда,
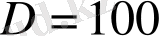 см және
см және
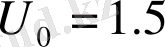 м/сек болған кезде құйынмен цилиндрден жұлқыну жиілігі
м/сек болған кезде құйынмен цилиндрден жұлқыну жиілігі
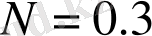 Гц болады. Екі жағдайда да
Гц болады. Екі жағдайда да
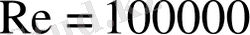
Ағын жылдамдығын қарапайым пьеземетрикалық Пито құбырсымен өлшеген кезде, немесе Прандтль құбырсымен өлшегенде, монометр бірінші мысалда ағыстың орташа жылдамдығына сәйкес келетін қысымды көрсетеді. Екінші жағдайда монометр көрсеткіші құйындармен жұлқыну жиілігіне тең, жиі болып тұратын аралықта тербеліп тұрады. Сондықтан дененің артындағы орталықтандырылған қозғалысты құйындарды он есеге дейін арттыратын уақыт мерзімі аралығынның артындағы:
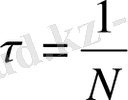 сек ізде орталандыру керек. Орталандырылған қозғалыс жылдамдығын
сек ізде орталандыру керек. Орталандырылған қозғалыс жылдамдығын
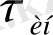 тұрақты инерциясы:
тұрақты инерциясы:
 шартын қанағаттандыратын аспаппен өлшеген жөн.
шартын қанағаттандыратын аспаппен өлшеген жөн.
Осы жұмыста орталандырылған қозғалыс ретінде нашар айнала ағатын дененің қабырғаларынан құйындардың жұлқыну мерзімімен салыстырғанда айтарлықтай үлкен уақыт аралығына орталандырылған қозғалыс меңзеліп отыр. Денеден алынумен жұлынатын құйындар ағыс бойымен төмен қарай таралатынын және шамамен калибр және одан ірі масштабтағы ара қашықтықта пульсациялар ұсақ масштабты турбулентті пульсацияларға айнала келе ғайып болатынын атап айту керек. Әр түрлі өлшемдік әдісінен нашар айнала ағатын дененің артындағы (4 суретті қараңыз) кері ағыс аймағының
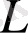 ұзындығын:
ұзындығын:
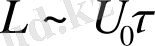 түрінде жазыла алады, мұндағы
түрінде жазыла алады, мұндағы
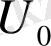 - сұйықтықтың қатпарлы ағысының жылдамдығы,
- сұйықтықтың қатпарлы ағысының жылдамдығы,
 - дененің артындағы іздегі сұйықтық қозғалысымен байланысты сипатқа тән уақыты. Нашар ағатын денелер үшін осындай уақыт болып олардың беткі қабаттарынан құйындардың жұлқыну уақыты бола алады:
- дененің артындағы іздегі сұйықтық қозғалысымен байланысты сипатқа тән уақыты. Нашар ағатын денелер үшін осындай уақыт болып олардың беткі қабаттарынан құйындардың жұлқыну уақыты бола алады:
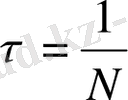 . Бірақ көрсетіліп қойғандай,
. Бірақ көрсетіліп қойғандай,
 ретіндегі
ретіндегі
 санының мәні аймағында Струхаль саны
санының мәні аймағында Струхаль саны
 және
және
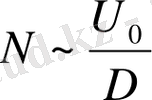 . Осыдан келе,
. Осыдан келе,
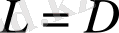 яғни, кері ағыстардың аймағының салыстырмалы ұзындығы
яғни, кері ағыстардың аймағының салыстырмалы ұзындығы
 ретіндегі
ретіндегі
 санының мәні аймағында, мұндағы
санының мәні аймағында, мұндағы
 болған кезде тұрақты.
болған кезде тұрақты.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz