Мәтіндік есептерді талдау және шешу әдістері: кезеңдер мен теңдеулерге негізделген тәсілдер


Мәтіндік есеп және оны шешу.
Мәтіндік есептердің математикада алатын өз орыны бар. Мұндай есептер әртүрлі болып келеді. Олар, күнделікті тұрмыстан алынған қарапайым есептер, жан-жақты ойлануды қажет ететін логикалық есептер т. б.
Жалпы, мәтіндік есептерді қалай шешуге болады?
Егер кез келген есептің шартына назар аударар болсақ, онда бірнеше талаптармен белгілі бір сұраққа жауап беру керек екенін көреміз. Кейде есептің бір шарт емес, бірнеше қарпайым шарттардан тұратынын байқаймыз. Сондықтан есепті шешер алдында оның шартына мұқят назар аударып, қандай талаптарды ескере отырып, қандай сұрақтарға жауап беру керек екенін зерделеп алған жөн. Мұны бір сөзбен « есепті талдау » деп атауға болады. Бұл есепті шешу процесіндегі бірінші кезең.
Еспті талдауды қалай жүзеге асыруға болады?
Мысалы, мына төмендегі мәтіндік есепті талдап көрелік.
Есеп. Катер ағыс бойымен 20 км, ал ағысқа қарсы 20 км жүзді. Катердің осы жолға жоғалтқан уақыты, оның 40 км тынық суда жүзген уақытынан аз ба, әлде тең бе ?
Есеп шартын мұқят оқып, біз катердің және өзен ағысының жылдамдықтары жөнінде ештеңе айтылмағандығына көз жеткіземіз. Ал, бұл шамаларсыз есепті шешу мүмкін емес. Сондықтан ол шамаларды, біз белгісіз айнымалылар арқылы белгілеп аламыз. Катердің меншікті жылдамдығы Х км/сағ, ағыс жылдамдығы У км/сағ.
Енді есепке мына төмендегідей талдау жүргізуге болады.
- катердің меншікті жылдамдығы Х км/сағ;
- өзен ағысының жылдамдығы У км/сағ;
- катер ағыс бойымен 20 км жүзді;
- және ол ағысқа қарсы 20 км жүзді;
- катер барлық жолғасағат жоғалтты;
- катер тынық суда 40 км жүзді;
- осы жолға олсағат жоғалтты
Есептің талабы:
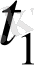 және
және
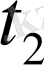 -ні салыстырып олар теңбе, егер тең болмаса қасысы үлкен, соны анықтаңыз.
-ні салыстырып олар теңбе, егер тең болмаса қасысы үлкен, соны анықтаңыз.
Есепті шешу процесіндегі келесі кезең, есептің схемалық жазбасын немесе графикалық сызбасын салу. Сызба барлық мәтіндік есептерде бірдей салына бермейді. Бірақ кейбір есептердің графикалық сызбасы есепті шешуге көмегін тигізетіні сөзсіз.
Мысал келтірейік.
Есеп. А станциясынанн В станциясына қарай жолаушы пойызы кетті. 2 сағат 30 минуттан кейін В станциясынан А станциясына қарай жүк пойызы жолға шықты. Екі пойыз С станциясында кездесті. Кездесуден соң жолаушылар пойызы 4 сағат 30 минут, ал жүк пойызы 3 сағат 40 минут жол жүрді. Олардың жылдамдықтары барлық жолда тұрақты болса, олар осы жолға жеке-жеке қанша уақыт жіберді?
Пойыздың қозғалыс сызбасы мына төмендегідей болады.
Әрине, графикалық сызба мәтіндік есепті толығымен алмастыра алмайды. Бірақ осы сызбаға сүйене отырып белгілі бір шешім қабылдауға болады.
Есепті талдау және оның графикалық сызбасын салу, есепті шешу әдісін табуға көмектеседі.
Есепті шешу әдісін табу, бұл есепті шешу процесінің үшінші кезеңіне жатады.
Табылған әдісті жүзеге асыру, төртінші кезең болып табылады. Бесінші кезеңге, есеп шешімін тексеруді жатқызуға болады. Есепті шешу процесінің алтыншы кезеңі есепті зеріттеу.
Шешімнің дұрыстығына көзжеткізіп және қажет деп табылса, есепті зеріттеп болған соң есептің жауабы тұжырымдалады, - бұл жетінші кезең.
Соңғы, сегізінші міндетті емес кезең есеп шешімін талдау.
Сонымен, есепті шешу процесін 8 кезеңге бөлуге болады.
1 кезең - есепті талдау;
2 кезең - есептің графикалық сызбасы;
3 кезең - есептің шешу әдісін іздеу;
4 кезең - есептің шешу әдісін жүзеге асыру;
5 кезең - есептің шешімін тексеру;
6 кезең - есепті зеріттеу;
7 кезең - есептің жауабын тұжырымдау;
8 кезең - есеп шешімін талдау;
Мәтінді есептерді мына төменднгі әдістерді қолдана отырып шеуге болады. Олар: «Мәтінді есептерді бір белгісізі бар сызықтық теңдеулердің көмегімен шешу», «Мәтінді есептерді пропорцияның көмегімен шешу», «Мәтінді есептерді квадрат теңдеулердің көмегімен шешу», «Мәтінді есептерді бөлшек рационал теңдеулердің көмегімен шешу», «Мәтінді есептерді екі айнымалысы бар теңдеулер жүйесінің көмегімен шешу», « Анализ және синтезді қолдана отырып мәтінді есептерді шешу ».
Есепті шешу процесі.
Мәтінді есептерді бір белгісізі бар сызықтық теңдеу құру арқылы шешу.
Мәтіндік есептерді бір айнымалысы бар сызықтық теңдеулердің
көмегімен шешуге болады.
ах=в түріндегі теңдеуді бір айнымалысы бар сызықтық теңдеу деп
атайды. . Мұндағы а және в - қандайда бір сандар. х - айнымалы.
Бір айнымалысы бар сызықтық теңдеулерді шешу үшін:
- Теңдеуде жақса болса, жақшаны ашып, болшек болған жағдайда теңдеудің екі жағын да бөлімдерінің ең кіші ортақ еселігіне көбейтіп түрлендіру керек.
- Айнымалысы бар мүшелерді теңдеудін бір жағына бос мүшелерді теңдеудің екінші жағына жинақтау керек.
- Теңдеудегі ұқсас мүшелерді біріктіріп, теңдеуді сызықтық теңдеуге келтіру керек.
- Теңдеудің екі бөлігін де айнымалының коэффициентіне бөліп, теңдеудің түбірін табу керек. .
Есептерді бір белгісізі бар теңдеу құрып шығарғанда алдымен есептің
шартындағы белгісіз шаманы әріп арқылы белгілейді. Содан соң есеп
шартын пайдалана отырып теңдеу құру керек. Теңдеуді шешу арқылы
белгісіздің мәні табылады. Есептің мағанасы бойынша табылған мәннің
есеп шартын қанағаттандыратындығы тексеріледі. Ең соңында жауабы
жазылады.
- мысал.
Кептірлгеннен кейін бидайдың самағы 8 пайыз кемиді.
Қамбаға 46 000 кг кептірілген бидай құю үшін кептірілген бидайдан
қанша алу қажет?
Шешуі:
Кептірілмеген бидай салмағынан кептірілгенде кемитін салмақты
азайтсақ, кепкен бидайдың салмағы шығады. Егер қажетті бидайды х кг
десек, кемитін 8 пайызды пайдаланып кептірілген бидайдың салмағын
өрнектеуге болады. Кептіру үшін қажет бидайдың салмағын х арқылы
белгілесек, онда кептіргеннен кейін салмақ
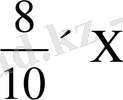 кг кемиді. Есептің
кг кемиді. Есептің
шарты бойынша тедеу құрамыз:
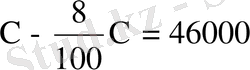 кг.
кг.
Бұл теңдеуді шешіп мынаны аламыз.
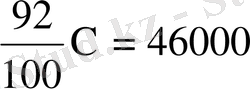 , х = 50 000 кг.
, х = 50 000 кг.
Жауабы: 50 000 кг бидай алу керек.
2 - мысал.
А және В екі станциясының ара қашықтығы 480 км. А станциясынан
шыққан жүк пойызы сағатына 48 км, В-дан шыққан жолаушы пойызы
сағатына 72 км жүреді.
- Егер екі пойыз бір мезгілде бір-біріне қарама-қарсы жолға шықса, олар
қанша сағаттан кейін кездеседі.
- Жолаушы пойызы жолға шыққан соң 25 мин өткенде жүк пойызы оған
қарама-қарсы жолға шықса, олар қанша уақыттан кейін кездеседі?
Шешуі:
- Егер екі пойыз х сағат өткенде кездесті десек, онда олардың жүрген
жолдары 48х және 72х болады. Екі пойыздың жүрген жолдарының
қосындысы екі станцияның ара қашықтығына тең болатынын пайдаланып
теңдеу құрамыз: 48х + 72х = 480. Осы теңдеуді шешіп мынаны табамыз.
120х = 480, х= 4.
Жауабы: 4 сағат.
- Жүк пойызы х сағат жүргеннен кейін жолаушы пойызымен кездеседі
десек, онда жолаушы пойызының жүк пойызы жолға шыққанға дейінгі
жүрген жолы
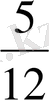
72 км, ал одан кейінгі жүрген жолы 48х. Есеп шарты
бойынша
, осы теңдеуді шешеміз, сонда 30 + 120х = 480, 120х = 480, 120х =450;
.
Жауабы: Жолаушы пойызы жолға шыққан соң 4 сағат 10 минут өткенде
жүк пойызымен кездеседі.
3 - мысал.
Бала үйінен қойлы ауылға бару үшін жаяу жолға шықты. Ол сағатына
4км жылдамдықпен жүріп отырды. 18 минут өткеннен кейін сол үйден
баланың ағасы велосипедке мініп 14 км/сағ жылдамдықпен оның артынан
шықты. Ағасы інісін қанша уақыттан кейін қуып жетеді?
Шешуі:
Ағасы х сағатта қуып жетеді десек, онда ағасы кездескеннен кейін
14х км жол жүреді. Ал інісі жолға ағасы кездескенге дейін 18 минут
бұрын шығып,
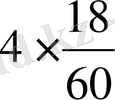 км және х сағатта тағыда 4х км жол жүреді. Сонымен, есеп шарты бойынша мынадай теңдеу құрамыз:
км және х сағатта тағыда 4х км жол жүреді. Сонымен, есеп шарты бойынша мынадай теңдеу құрамыз:
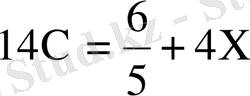
Теңдеуді шешкенде мынау шығады:
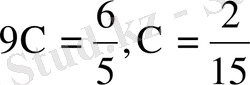 .
.
Жауабы: Ағасы інісін 8 минутта қуып жетеді.
4 - мысал.
Бір жұмысты Асан жеке өзі істесе, 24 сағатта, ал Үсен өзі жеке істесе, 16 сағатта бітіреді. Алдымен Асан жеке өзі 6 сағат істегеннен кейін қалған жұмысты екеуі бірігіп істесе, қанша сағатта бітіреді?
Шешуі:
Барлық жұмысты бір бүтін деп есептейміз. Асан мен Үсеннің сағатына қанша жұмыс істей алатыны белгілі. Егер Асан жеке өзі 6 сағат істегеннен кейінгі қалған жұмысты екеуі Х сағатта орындай алды десек, барлық жұмысты бір бүтін деп алғанда, Асан 1 сағатта жұмыстың
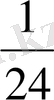 , 6 сағатта
, 6 сағатта
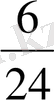 бөлігін бітіреді, ал бірлесіп істегендегі Асанның жұмысы
бөлігін бітіреді, ал бірлесіп істегендегі Асанның жұмысы
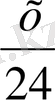 , Үсендікі
, Үсендікі
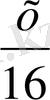 болады. Есеп шарты бойынша теңдеу құрамыз:
болады. Есеп шарты бойынша теңдеу құрамыз:
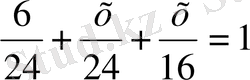 .
.
Теңдеуді шешеміз:
12 + 2х + 3х = 48,
5x = 36,
x = 7, 2
Жауабы: Қалған жұмысты Асан мен Үсен бірігіп 7 сағат 12 минутта бітіреді.
5-мысал.
Оқушылардың екі тобы картоп жинап жүр. Бір топта 47, ал екіншісінде 39 оқушы бар. Бұларға 40 оқушы көмекке келді. Әр оқушы өз еркі бойынша топтарға қосылды. Сонда бірінші топтағы оқушылар саны екіншіден екі есе артық болды. Көмекке келген балалар қалай бөлінген.
Шешуі:
Бір топқа х оқушы бөлінді, онда екінші ьопқа ( 40 - х ) оқушы бөлінген. Сонда бірінші топтағы оқушылар саны 47 + х, екіншісінде 39 + ( 40 - х ) болады. Есеп шарты бойынша теңдеу құрамыз:
47 + х = 2 ( 39 + ( 40 - х ) ) .
Теңдеуді шешсек,
47 + x = 78 + 2 ( 40 - x ),
47 + x = 78 + 80 - 2x,
3x = 111,
x = 37.
Жауабы: Бірінші топқа 37 оқушы, екінші топқа 3 оқушы көмекке келген.
Жаттығулар.
- 5 дәптер мен 3 қарындашты сатып алу үшін 21 теңге төленді. Бір қарындаштың бағасы 2 теңге болса, бір дәптер қанша тұрады?
- Екі қаланың арасы 284 км. Жүк пойызы сағатына 48 км жылдамдықпен А қаласынан С қаласына қарай жолға шықты, одан кейін 1 сағат өткен соң оған қарама-қарсы сағатына 70 км жылдамдықпен жолаушылар пойызы жолға шықты. Олар жолаушылар пойызы жолға шыққан соң неше сағаттан кейін кездеседі?
- Арқан тарту ойынының бір жағында 20, екінші жағында 16 адам бар. Ойында жеңіп шығу үшін бір жағындағы адам саны екінші жағынан 2 есе артық болуы тиіс болса, арқанның бір жағынан екінші жағына қанша адам ауысу керек?
- Екі қамбада барлығы 4 т бидай бар. Бір қамбаға 4000 т бидай әкелді, екіншісінен 8000 т бидайды тасып кетті. Сонда екі қамбадағы бидайдвң тонна саны бірдей болды. Бұрын осы екі қамбаның әрқайсысында қанша тонна бидай бар еді?
- Зауыт қараша айында 20500 дана машина бөлшегін жасады. Бұл өткен жылғы қарашады жасалғанның екі есесінен тағы 1500 данасы артық. Осы зауыт өткен жылғы қарашада қанша дана машина бөлшегін жасаған еді?
- Құрғақ жемді су қосып бөктіргеннен кейін салмағы 150 пайызға арытты. 36 т бөктірілген жем дайындау үшін қанша тонна құрғақ жем алу қажет?
- Ара қашықтығы 260 км А және В қалаларынан бір уақытта қарама-қарсы екі автобус жолға шығып, 2 сағаттан кейін жолыққан, А қаласынан шыққан автобус В қаласынан шыққан автобусқа қарағанда сағатына 10 км артық жүрген. В қаласынан шыққан автобустың жылдамдығын тап.
- Ара қашықтығы 750 км екі қаладан бір уақытта қарама-қарсы бағытта екі ұшақ ұшып шығып, жарты сағаттан кейін кездесті. Бірінші ұшақтың жылдамдығы екіншісінің жылдамдығынан 2, 5 есе артық. Ұшақтардың жылдамдықтарын тап.
- Бір шағын мекеменің 108 га суармалы жері, 54 га шөлейт жері бар. Енді шөлейт жер суарылатын жердің 20 пайызы болатындай оған тоған жүргізді. Суғарылтын жерге айналдырылған неше гектар шөл атыз суғарылатын болды?
- Бір қамбада 30 т астық бар. Бірінші қамбадағы астық екіншісіндегі астықтың 1, 5 есесіндей болуы үшін, осы екі қамбаға барлығы 80 т астық тасып әкелінуі керек. Сонда әр қамбаға неше тонна астық тасып әкелінген?
- Құрлысшылардың екі тобы су құбырын жөндеп жүр. Жұмысшылардың бірінші ьобы жұмысты жеке өзі істесе 12 күнде, ал екіншісі 18 күнде бітіреді. Егер осы екі топ су құбырының екі басынан түсіп істесе, олар су құбырын неше күнде жөндеп бітіреді?
- Екі таңбалы санның бірлігі ондығынан екі есе артық. Егер осы санның бірлігі мен ондығының орындарынын ауыстырып қойса, онда шыққан екі таңбалы санның бұрынғы екі таңбалы саннан 36-сы артық болады. Осы санды тап.
Мәтінді есептерді пропорцияның көмегімен шешу.
Қарапайым мәтіндік есептерді пропорцияның көмегімен шешуге болады.
Екі қатынастың теңдігі пропорция деп аталады.
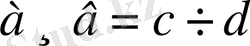 немесе
немесе
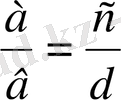 мұндағы
мұндағы
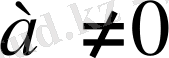 ,
,
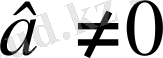 ,
,
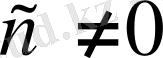 .
.
а мен d-ны пропоцияның шеткі мүшелері, в мен с-ны ортаңғы мүшелері деп
атайды.
Пропорция дегеніміз өзара тең қатынастар болғандықтан,
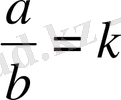 және
және
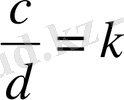 деп белгілеу орынды. Мұндағы k-пропорционалдық коэффициент деп
деп белгілеу орынды. Мұндағы k-пропорционалдық коэффициент деп
аталады.
1-мысал.
Үшбұрыштың периметрі 36 см. Оның қабырғаларының ұзындықтары 2:3:4
қатынасындай. Үшбұрыштың қабырғаларының ұзындықтарын табу керек.
Шешуі:
- Ізделінді шаманың сандық мәні ондағы үлес санына тәуелді. Сондықтан алдымен толық шамадағы барлық үлес санын табу керек.
Ол 2+3+4=9. толық шамада 9 үлес бар.
- Толық шаманың бір үлесіне сәйкес мәнін табамыз, ол.
- Үшбұрыш қабырғакларының тиісті үлес ( қатынас ) санына сәйес ұзындықтарын табамыз. Үшбұрыштың:
бірінші қабырғасы
(см)
екінші қабырғасы
(см)
үшінші қабырғасы
(см)
Пропорциямен жазсақ:
немесе
;
;
.
Пропорционалдық коэффициент 4 саны.
Жауабы: 8 (см ), 12 ( см ), 16 ( см ) .
2-мысал.
Жұмысшы еңбек ақысының 11 пайызын жұмсағаннан кейін, оның қолында 7120 теңге қалды. Жұмысшының еңбек ақысы қанша теңге болғаны?
Шешуі:
Жұмысшының айлық еңбек ақысы Х теңге болсын. Есеп шарты бойынша мынадай пропорция аламыз:
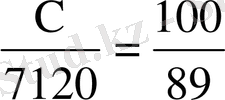
Осы пропорцияны мына түрде жазамыз: 89X = 712000, X = 8000.
Жауабы: Жұмысшының айлық еңбек ақысы 8000 теңге.
3-мысал.
Тракторшылар бригадасы бір күде 24 гектар жер жыртты. Бұл барлық егістіктің 15 пайызын құрайды. Барлық егістіктің көлемі қандай?
Шешуі:
Барлық егістіктің көлемін Х гектар деп алып, мынадай пропорция құрамыз:
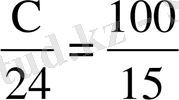 .
.
Алынған пропорцияны мына түрде жазамыз: 15Х = 2400, X = 160.
Жауабы: Барлық егістіктің көлемі 160 гектар.
4-мысал.
Сүттен 21 пайыз қаймақ, ал қаймақтан 24 пайыз май алынады.
630 кг май алу үшін қанша кг сүт керек.
Шешуі:
Белгісіз шаманы х кг деп белгілейміз де, есеп шарты бойынша теңду құрамыз.
,
,
.
Жауабы: 12500 кг сүт керек.
5-мысал.
Етті қайнатқанда, ол өз салмағының 35 пайызын жоғалтады.
520 г піскен ет алу үшін қанша шикі ет керек.
Шешуі:
Ізделінді шикі еттің салмағын х г деп алып, есеп шартын пайдалана отырып мынадай теңдеу құрамыз.
,
,
,
.
Жауабы: 800г шикі ет қажет.
Мәтінді есептерді квадрат теңдеулердің көмегімен шешу.
Көптеген мәтіндік есептерді квадрат теңдеулерді қолданып шешуге болады. Математикада квадрат теңдеулердің қолданылуы өте ауқымды, сондықтан оларды шеше білудің маңызы зор.
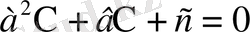 түріндегі теңдеуді квадрат теңдеу деп атайды. Мұндағы х - айнымалы, а, в, с - сандар ( а = 0 ), а - бірінші коэффициент, в - екінші коэффициент, с - бос мүше деп аталады.
түріндегі теңдеуді квадрат теңдеу деп атайды. Мұндағы х - айнымалы, а, в, с - сандар ( а = 0 ), а - бірінші коэффициент, в - екінші коэффициент, с - бос мүше деп аталады.
Квадрат теңдеудің түбірлері мына төмендегі формула бойынша табылады
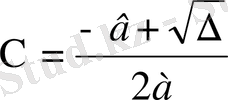 ,
,
мұндағы D - ны дискриминант деп атайды. D=b - 4ac.
Қарастырылып отырған теңдеудің дискриминанттың мәніне байланысты үш түрлі шешу жолы бар.
1) D>0 болса, онда теңдеудің екі түбірі бар.
2) D=0 болса, онда теңдеудің бір ғана түбірі бар.
3) D<0 болса, онда теңдеудің нақты түбірі жоқ.
Мәтіндік есептерді квадрат теңдеулердің көмегімен шешу үшін, алдымен есеп шартындағы белгісіз шаманы айнымалымен белгілеп алып, одан соң шартты пайдалана отырып теңдеу құру керек. Осы құрылған квадрат теңдеудің түбірлерін табамыз. Табылған түбірлердің есеп шартын қанағаттандыратын түбірін алып, оны жауап ретінде жазамыз.
1-мысал.
120 санын екі санның көбейтіндісі түрінде жазыңдар, сонда олардың
бірі екіншісінен 2-ге кем болсын.
Шешуі:
Алдымен, бірінші санды Х арқылы, екінші санды ( Х-2 ) деп белдгілеп
аламыз. Содан соң есеп шарты бойынша теңдеу құрамыз.
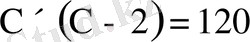 ,
,
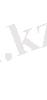
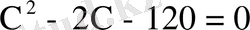 . Осы алынған квадрат теңдеудің түбілерін
. Осы алынған квадрат теңдеудің түбілерін
табамыз. Ол үшін алдымен квадрат теңдеудің дискриминантын есептейміз:
D
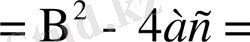 4+480=484.
4+480=484.
Шыққан дискриминантты түбірлердің формуласына қойып, мынаны
табамыз.
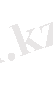
 ;
;
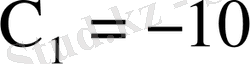 ,
,
 .
.
Табылған түбірлердің екуі де есеп шартын қанағаттандырады. Соныдықтан
бірінші сан -10 болса, екінші сан -12 немесе бірінші сан 12 болса, екінші
10 болады.
Жауабы: ( -10; -12 ) немесе ( 10; 12 )
- мысал.
Тік төртбұрыштың ұзындығы енінен 4 (см ) артық, ал ауданы 60
-ге тең. Тік төртбұрыштың периметрін табыңдар.
Шешуі:
Тік төрбұрыштың енін Х (см ), ал оның ұзындығын ( Х+4 ) см -ге тең деп аламыз. Сонда есеп шарты бойынша оның ауданы мынаған тең болады.
Х ( Х + 4 ) = 60 ;
.
Осы квадрат тедеудің түбірлерін табамыз.
D =
16 + 240 = 256,
,
,
.
Бұл екі түбірдің бірі, яғни -10 есеп шартын қанағаттандырмайды. Сондықтан, тік төртбұрыштың ені 6 (см ) - ге тең болса, онда оның сәйкес
ұзындығы (Х + 4 ) = 6 + 4 = 10 (см) болады. Ізделініп отырған тік төртбұрыштың периметрі мынаған тең болады.
Р = 2 ( 6 + 10 ) = 32 (см ) .
Жауабы: 32 ( см ) .
3-мысал.
Тік бұрышты үшбұрыштың катеттерінің бірі гипотенузасынан 3 см кем, ал екінші катет гипотенузадан 6 см кем. Гипотенузаны табыңдар.
Шешуі:
Есеп шарты бойынша тік бұрышты үшбұрыштың гипотенузасын Х (см ) деп белгілесек, онда оның бір катеті ( Х-3 ) см және екінші катеті ( Х-6 ) см болады. Пифагор теоремасы бойынша мына төмендегідей теңдік аламыз.
,
,
,
Шыққан квадрат теңдеудің түбірлерін табамыз.
D = 324-180=144,
,
,
.
Табылған түбірлердің бірі, яғни 4 саны есеп шартын қанағаттандырмайды.
Сондықтан есетің шартын қанағаттандыратын екінші түбір 15 саны есептің жауабы болып табылады.
Жауабы: Гипотенузаның ұзындығы 15 см-ге тең.
4-мысал.
Екі таңбалы санның ондық цифры оның бірлігінен 2-ге артық. Егер осы санды өзінің цифрларының қосындысына көбейтсек, онда 900-ге тең болады. Осы екі санды табу керек.
Шешуі:
Егер осы екі таңбалы санның одық цифры х-ке тең болса, онда бұл санның бірлігі х-2 -ге тең болады. Сондықтан бізге керекті ондық сан 10х+х+х-2 = 11х-2 түрінде жазылады. Сонымен қатар (11х-2) (х+х-2) =900 болуы керек. Осыдан
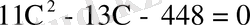 квадрат теңдеуін аламыз. Бұл теңдеудің түбірлері
квадрат теңдеуін аламыз. Бұл теңдеудің түбірлері
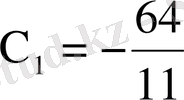 ,
,
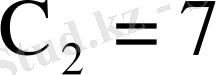 болады. Есептің шарты бойынша бізді
болады. Есептің шарты бойынша бізді
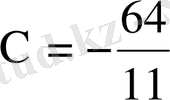 түбірі қанағаттандырмайды. Сондықтан X=7 және X-2=5 болуы керек, яғни ізделінді сан - 75. шынында да 75 ( 7+5 ) = 900.
түбірі қанағаттандырмайды. Сондықтан X=7 және X-2=5 болуы керек, яғни ізделінді сан - 75. шынында да 75 ( 7+5 ) = 900.
Жауабы: 75.
5 - мысал.
Клуб залындағы орындықтардың қатарлар саны қанша болса қатардағы орындар саны сонша. Егер қатарлар санын екі есе арыттырып, қатардағы орындықтар санын 10-ға кемітсе, онда барлық орын саны 300-ге көбейеді.
Клуб залындағы қатарлар саны қанша?
Шешуі:
Клуб залындағы қатарлар саны мен қатардағы орындықтар санын х деп белгілеп аламыз да, барлық орындар санын
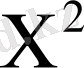 -қа тең дейміз.
-қа тең дейміз.
Сонда есеп шарты бойынша мынадай теңдеу құрамыз.
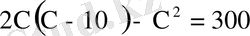 ,
,
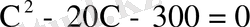 .
.
Алынған квадрат теңдеуді шешіп, оның түбірлерін табамыз.
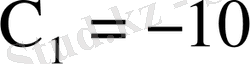 ,
,
 .
.
-10 саны есеп шартына қайшы, сондықтан 30 саны ғана есептің жауабы болады.
Жауабы:
Клуб залындағы қатарлар саны 30-ға тең.
Мәтінді есептерді бөлшек рационал теңдеулердің көмегімен шешу.
Кейбір мәтіндік есептер жүрілген жол, жылдамдық, уақыт, орындалған жұмыс, аудан, көлем т. б. ұғымдарымен беріледі. Мұндай есептерді бөлшек рационал теңдеулердің көмегімен шешкен қолайлы. Әдетте, бөлшек рационал теңдеулерді теңдеулердің мәндестігі қасиеттерін қолдана отырып, оларды бүтін өрнектерге келтіріп шешеді.
Осындай процесс барысында біздерге әртүрлі теңдеулерді қолдануымызға тура келеді. Сндықтан есеп соңында бөгде түбірлер, яғни берілген теңдеуді қанағаттандырмайтын түбірлер пайда болуы мүмкін. Бөгде түбірлерді ескеру үшін, есептің соңында алынған шешімдерді мүмкін мәндер жиынымен салыстырып, берілген есептің жауабын аламыз немесе шыққан шешімдерді теңдеуге қойып, тексеру арқылы бөгде түбірлерді бөліп тастауға болады.
Бөлшек рационал теңдеулерді шешуді мынадай ережелермен орындаған тиімді:
а) Теңдеудің құрамындағы бөлшектердің бөлоімдерін нөлге айналдыратын айнымалының мәндерін анықтап, теңдеудің мүмкін мәндерінің жиынын табу керек;
ә) Берілген теңдеудегі бөлшектің ортақ бөлімдерін анықтап, теңдеуді осы ортақ бөлімге көбейтеді. Осылай бүтін теңдеуді бүтін теңдеумен алмастыру керек;
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz