Алгебралық теңдеулердің шешудің жанама әдісі

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 12 бет
Таңдаулыға:

Жоспар

I. Кіріспе 3

II. Негізгі бөлім . 4

2. 1. Алгебралық теңдеулердің шешудің жанама әдісі . …. 4

2. 2. Теорема . . . 7

2. 3. Мысалы . 10

III. Қорытынды бөлім . 14

IV. Ќосымша 1 . . 15

V. Қолданылған әдебиеттер 17

Кіріспе

Бұл жұмыста

ƒ(z) =0

теңдеуінің түбірлерін табудың кейбір әдістері қарастырылады. Мұндағы z- нақты немесе комплекс сан, ал ƒ(z) -осы z аргументін тәуелді көпмүше немесе трансцендентті функция.

Егер ƒ(z) көпмүше болса, онда 5-дәрежелі көпмүшеге дейін ғана ƒ(z) =0 теңдеуінің түбірлерін тиянақты бір формулалар арқылы дәл есептеуге болатыны белгілі. Басқа жағдайларда мұндай теңдеудің түбірлерін жуық шамамен табуға тура келеді. Ол үшін төмендегі екі мәселені шешу қажет болады:

1) түбірлерді айыру, яғни ішінде тек бір ғана түбір жататын кішкене облыстарды анықтау;

2) теңдеудің түбірлерін берілген дәлдікпен есептеп шығару.

Жанамалар (Ньютон) әдісі

Айталық,

(x) =1/f’(x)

болсын және (x) функциясы үшін

1) ƒ(x) функциясы x нақты аргументтің нақты функциясы;

2) ƒ(x), ƒ'(x) және ƒ''(x) -үзіліссіз функциялар, ал ƒ'(x) жәнеƒ''(x) туындылары осы R ⁰ -де өз таңбаларын өзгерітпейді;

3) 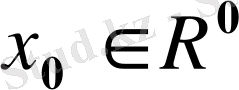болғанда ƒ(x ₀ ) *ƒ''(x ₀ ) >0 теңсіздігі орындалады;

шарттар орындалсын.

Ол жағдайда х= (x) теңдеуі мына түде жазылады:

X= (x) =x- 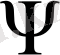(x) f(x) =x-f(x) /f’(x) .

Енді ’(x) туындысын есептейміз:

’(x) =1-[f(x) ] ² -f *f’’(x) /[f’(x) ] ² .

Теңдікте х=x* десек, онда ’(x*) =0 болады. Демек, R ⁰ аралығында

’(x) Equation. 3 <1

теңсіздігі орындалады. Соны мен, егер х ₀ εR ⁰ болса, онда

x= х _R-1 -f(x _R-1 ) /f’(x _R-1 ), R=1, 2, . . (1)

тізбегі жинақты болады және оның шегі х= (x) немесе f(x) =0 теңдеуінің х* түбіріне тең. Есептеу математикасында (1) алгоритмі Ньютон әді сі деп аталады. Оған төмендегідей геометриялық мағына беруге болады: х _R жуықтауы M _R-1 (x _R-1 , f(x _R-1 ) ) нүктеде y=f(x) қисық сызығына жүргізілген жанаманың 0 _х өсімен қиылысу нүктесінің абсциссасына тең (суретте көрсетілген) . Сондықтан да Ньютон әдісін кейде жанамалар әдісі деп те атайды.

Ньютон әдісі арқылы f(x) =0 теңдеуінің нақты түбірлерімен қатар комплекс түбірлерін де табуға болады. Ол үшін бастапқы х ₀ нүктесі нақты емес, комплекс сан түрінде алу керек.

Жанамалар әдісінде бастапқы х ₀ нүктесі f(x ₀ ) *f’’(x ₀ ) >0 шартына сай таңдап алады. Себебі f(x ₀ ) f’’(x) <0 болса, онда х ₀ - иілу нүктесі болады да нәтижеде әдіс х* түбірге жинақталмауы мүмкін (суретті қараңыздар) .

Ньютон әдісінде ’(x *) =0, ал жалпы жағдайда ’’(x*) 0 болуы мүмкін. Демек, ол екінші ретті интерациялық әдіс.

Ньютон әдісінің e _R =x _R -x* қателігін бағалаймыз.

Ол үшін алдымен 0=f(x*) =f(x _R-1 ) +f’(x _R-1 ) (x*-x _R-1 ) +1/2f’’(ξ) (x-x _R-1 ) ²

Тэйлор жіктеуінен төмендегі қатынасты аламыз:

f(x _R-1 ) /f’(x _R-1 ) =x _R-1 -x*-1/2*f’’(ξ) /f’(x _R-1 ) *(x*-x _R-1 ) ² (а)

Енді x _R -x*=e _R , x _R-1 -x*=e _R-1 деп белгілейік. Онда (1) рекурренті формуладан (а) теңдігін пайдаланып, әдістің e _R және e _R-1 қателіктерінің арасындағы мынандай байланысты алу қиын емес:

E _R =1/2*f’’(ξ) /f’(x _R ) *e ² _R-1 .

Айталық,

M ₁ =min f’(x) , M ₂ =max f’’(x)

болсын.

Бұл жағдайда x _R -x* ≤M ₂ /2M ₁ x _R-1 -x* ²

Теңсіздігі орындалады, яғни Ньютон әдісі жылдам жинақталады.

f(x=0)

теңдеуінің ξ түбірі [a, b] кесіндісінде бөлінген, f’(x) және f’’(x) үзіліссіз және а≤х≤в аралығында белгілі бір анықталған таңбаларын сақтайды.

x _n ⋲ξ(a≤x _n ≤b) қандайда бір n-ші түбірдің жуық мәнін тауып, біз оны Ньютон әдісімен келесі түрде нақтылай аламыз.

ξ=x _n +h _n , (2)

деп алсақ, мұндағы h _n аз шама деп есептейміз. Бұдан, Тейлор формуласын қолданып, келесіні аламыз:

0=f(x _n +h _n ) ⋲f(x _n ) +h _n f’(x _n ) .

Яғни h _n =-f(x _n ) /f’(x _n ) .

Бұл түзетуді (2) формулаға енгізсек, келесі жуықталған түбірді ретімен табамыз.

X _n+1 =x _n -I(x _n ) /I’(x _n ) (n=0, 1, 2, . ., ) (3)

Ньютон әдісінің геометриялық жағынан y=f(x) доға қисығын жанамамен алмастырғанға пара-пар, ол қисықтың кейбір нүктелерінен өтеді. Шынында да, анықтау үшін, а≤х≤в және f(b) >0 болғанда f’’(x) >0 (сурет 18)

Мысалыға, f(x ₀ ) f’’(x ₀ ) >0 үшін х ₀ =в деп алайық. В ₀ [x ₀ ; f(x ₀ ) ] нүктесінде y=f(x) қисығына жанама жүргізейік. Ξ түбірінің х ₁ бірінші жуық мән ретінде осы жанаманың 0 _х өсімен қиылысу нүктесінің абсциссасын алайық.

B ₁ [x ₁ , f(x ₁ ) ] нүктесі арқылы тағыда жанама жүргізейік, оның абсциссасының қиылысу нүктесі бізге ξ түбірінің екінші жуық х ₂ мәнін береді және т. с. с. (18 сурет) В _n [x _n , f’(x) ] (n=1, 2, . ., ) нүктесінде жанама теңдеуі

y-f(x _n ) =f’(x _n ) (x-x _n ) .

Болатыны көрінеді. y=0, x=x _n+1 деп алып, (3) формуланы аламыз:

X _n+1 =x _n -f(x _n ) /f’(x _n ) .

Егер біздің жағдайда х ₀ =a деп алсақ, және f(x ₀ ) f’’(x ₀ ) <0 десек, онда А[a, f(a) ] нүктесінде y=f(x) қисығына жанама жүргізіп біз [a, b] кесіндісінен тыс жатқан х ₁ нүктесін алар едік. (18 сурет ) , яғни бұл бастапқы мән шешімінде Ньютон әдісі қолданылмайды. Осыдан берілген жағдайда х ₀ жақсы бастапқы жуық мәні болып, ол үшін мына теңсіздік орындалса

f(x ₀ ) f’’(x ₀ ) >0 (4)

Бұл ереже жалпы екенін дәлелдейік.

Теорема . f’(x) және f’’(x) нөлден өзгеше және а≤х≤в болғанда нақты қанағаттандыратын х ₀ [a, b] бастапқы жуықт Ньютон әдісімен (3) формула теңдеуінің кез келген тура дәрежедегі бір ξ түбірін есептеуге болады.

Дәлелдеуі . Мысалыға, а≤х≤в үшін қалған жағдайлар ұқсастықпен қарастырылады. f(a) <0, f(b) >0, f’(x) >0, f’’(x) болсын.

(4) теңсіздігіне сәйкес f(x ₀ ) >0 аламыз (мысалыға, х ₀ =в деп алуға болады. ) Математикалық индукция әдісімен барлық жуықтаулар x _n >ξ(n=0, 1, 2, . ., ) және f(x _n ) >0 екенгін дәлелдейік . Шынында да, алдымен, х ₀ >ξ. Енді х _n >ξ болсын.

ξ=x _n +(ξ-x _n )

деп алсақ. Тейлор формуласын қолданып төмендегіні аламыз

0=ƒ(ξ) =ƒ(x _n ) +ƒ’(x _n ) (ξ-x _n ) +1/2ƒ’’(c _n ) (ξ+x _n ) ² , (5)

мұндағыξ<c _n <x _n .

ƒ’’(x) >0 болғандықтан онда

ƒ(x _n ) +ƒ’(x _n ) (ξ-x _n ) <0

және

x _n+1 =x _n -ƒ(x _n ) /ƒ’(x _n ) >ξ,

яғни дәлелденді.

(3) формуладан, ƒ(x _n ) және ƒ‘(x _n ) белгілерін ескере отырып, x _n+1 <x _n (n=0, 1, 2, . ., ) теңсіздігін аламыз, яғни тізбектелген х ₀ , х ₁ , . . x _n , жуықтаулары монотонды кемімелі шектелген тізбек құрайды. Осыдан, ξ=x _n бар.

(3) тендігінде шекке көшіп ξ=ξ-ƒ(ξ) /ƒ’(ξ) аламыз, яғни (ξ=0) . Бұдан талап етілген дәлелдеуіміз ξ=ξ.

Сондықтан, Ньютон әдісін қолданғанда келесі ережені ұстану керек:

ƒ’’(x) белгісіндегі кордината сол белгіні қабылдайтындай, (а, в) интервалында х ₀ бастапқы нүктесі ретінде сондай соңы алынады.

Ескерту . Егер:

1) ƒ(x) функциясы -∞<x<+∞ аралығында анықталған және үзіліссіз; 2) ƒ(a) ƒ(b) <0;

3) a≤x≤b ƒ’(x) ≠0;

4) ƒ’’(x) бар және тұрақтьы белгіні сақтайды, Онда, (а, в) интервалында жатқан, ƒ(x) =0 теңдеуінің түбірін табу үшін Ньютон әдісін қолданған бастапқы х ₀ жуықтауы ретінде c [а, в] кез-келген мәнін алуға болады. Дербес жағдайда, х ₀ =a және х ₀ =в деп алуға болады.

Шынында да, мысалы а≤х≤в болғанда ƒ’(x) >0, ƒ’’(x) >0 және x ₀ =c, мұндағы а≤с≤в. Егер ƒ(c) >0 болса, онда ξ=c түбірі және есеп шешіледі.

Егер ƒ(c) >0, онда жоғарыда келтірілген және с бастапқы мәнімен Ньютон процесі ξ ( а, в) түбіріне келеді. Сонымен егер ƒ(c) <0, онда төменгі мәнді табамыз.

х ₁ =х ₀ -ƒ(х ₀ ) /ƒ’(х ₀ ) =с-ƒ(с) . ƒ’(с)

Тейлор формуласын қолданып төмендегіні алмыз

ƒ(x ₁ ) =ƒ(c) -ƒ(c) /ƒ’(c) *ƒ’(c) +1/2[ƒ(c) /ƒ’(c) ] ² ƒ’’(c) =1/2[ƒ(c) /ƒ’(c) ] ² ƒ’’(c) >0,

мұндағы с-с және х ₁ арасындағы кейбір аралық мәні. Осыдан

ƒ(x ₁ ) ƒ’’(x ₁ ) >0.

ƒ’’(x) >0 шартынан сонымен қатар, ƒ’(x) -өспелі функция екені шығады және x>a, болғанда ƒ’(x) >ƒ’(a) >0 шығады. Яғни Ньютон процесі үшін ξ>c≥a болатын ƒ(x) функцияның кез келген ξтүбіріне сәйкес келес бастапқы мән реттенді х ₁ алуға болады. Х>а болғанда ƒ’(x) туындысының сандық мәні неғұрлым көп болса, (n+1) -ші жуықтап алу үшін n-ші жуықтауға қосылатын түзету соғұрлым аз екені көрінеді. Сондықтан Ньютон әдісін әсіресе берілген түбірдің аймағында функцияның графиігі үлкен бұралым алғанда қолдану ыңғайлы . Бірақ егер ƒ’(x) туындысының түбір жанында сондықтан мәні аз болса, онда түзетулер үлкен болады, және бұл әдіспен түбірді есептеу өте ұзақ болып кетуі мүмкін, кейде тіпті мүмкін емес. Яғни егер y=ƒ(x) қисығы 0 _х өсімен қиылысу нүктесінің жанында көлденеңдеу болса, онда ƒ(x) =0 теңдеуін шешу үшін Ньютон әдісі қолданылмайды. X _n n-ші жуықтауының қателігін бағалау үшін мынандай

ξ-x _n ƒ(x _n ) /m ₁ (6)

жалпы формуласын қолдануға болады, мұндағы m ₁ -[a, в] кесіндісінде

ƒ’(x) ең кіші мәні. X _n жуықтауын тура бағалау үшін бір формула шығарайық. Тейлор формуласын қолдана төмендегіні аламыз:

ƒ(x _n ) =ƒ[x _n-1 +(x _n -x _n-1 ) ] =ƒ(x _n-1 ) +ƒ’(x _n-1 ) (x _n -x _n-1 ) -1/2ƒ’’(ξ _n-1 ) (x _n -x _n-1 ) ² , (7)

мұндағы ξ _n-1 (x _n-1 , x _n ) . x _n жуықтауын анықтауда келесіні аламыз:

ƒ(x _n-1 ) +ƒ’(x _n-1 ) (x _n -x _n-1 ) =0,

онда (7) -ден ƒ(x _n ) 1/2M ₂ (x _n -x _n-1 ) ² аламыз, мұндағы M ₂ -[а, в] кесіндісінде ƒ’’(x) ең үлкен мәні.

Яғни (6) формулаға жүгінсек ақырында төмендегі формуланы аламыз.

ξ-х _n M ₂ 2m ₁ (х _n -х _n-1 ) (8)

Егер Ньютон процесі жинақты болса, онда х _n -x _n-1 →0 (4) n→∞ ұмтылғанда. Сондықтан n≥N болғанда

ξ-x _n ≤ x _n -x _n-1 ,

Яғни, x _n-1 және x _n жуықтаудың бекітілген бастапқы ондық мәндері кейбір жуықтаудан бастап дұрыс болып шығады.

Байқайтынымыз, жалпы жағдайда x _n-1 және x _n дәл ε екі жуықтау тізбегінің сәйкестігі тура сол дәлдікпен x _n және нақты түбір сәйкес келетініне кепілдік бермейді. Сонымен қатар екі x _n және x _n+1 жуықтау тізбегінің абсолютты қателіктерін байланыстыратын формула шығарайық. (5) формуладан аламыз:

ξ= x _n -ƒ(x _n ) /ƒ’(x _n ) -1/2*ƒ’’(c _n ) /ƒ’(x _n ) (ξ-x _n ) ² ,

мұндағы с _n (x _n , ξ) . Бұдан, (3) формуланы ескере отырып, мынаны аламыз:

ξ-x _n+1 =-1/2*ƒ’’(c _n ) /ƒ’(x _n ) *(ξ-x _n ) ²

және (9)

ξ-x _n+1 ≤M ₂ /2m ₁ (ξ-x _n ) ² .

формуласы шығады. (9) формула Ньютон процесінің тез жинақтылығын қамтамасыз етеді, егер бастапқы х ₀ жуықтау төмендегідей болса,

M ₂ /2m ₁ ξ-x ₀ ≤q<1.

1. мысалы ƒ(x) ≡x ⁴ -3x ² +75x-10. 000=0 теңдеуінің бес нақты белгісімен теріс түбірін Ньютон әдісін есептеніз.

Шешуі : теңдеудің сол жағында x=0, -10, -100, . ., деп алып, ƒ(0) =-1,

ƒ(-10) =-1050, ƒ (-100) ⋲+10 ⁸ аламыз.

Яғни ізделінді ξ түбірі -100<ξ<-10 интервалында жатыр. Табылған интервалды қысқартатын болсақ, ƒ(-11) =34536, онда -11<ξ<-10. осы ақырғы интервалда ƒ’(x) <0 және ƒ’’(x) >0. ƒ(-11) >0 және ƒ’’(-11>0) болғандықтан, онда бастапқы жуықтау ретінде х ₀ =-11 деп аламыз. X _n (n=1, 2, . ., ) тізбектеп жуықтауын келесі схема бойынша есептейміз.

n: n

Xn: X _n

ƒ(xn): ƒ(x _n )

ƒ’(xn): ƒ’(x _n )

hn=-ƒ(xn) /ƒ’(xn): h _n =-ƒ(x _n ) /ƒ’(x _n )

Xn:

-11

-10, 3

-10, 27

-10, 261

ƒ(xn):

3453

134, 3

37, 8

0, 2

ƒ’(xn):

-5183

-4234

-4196

hn=-ƒ(xn) /ƒ’(xn):

0, 7

0, 03

0, 009

n=3 мәніне тоқталып, ƒ(x _n +0, 001) =ƒ(-10, 260) (5) мәнінің белгісін тексереміз. ƒ(-10, 260) <0 болғандықтан, онда -10, 261<ξ<-10, 260, және осы сандардың кез-келген ізделінді жуықтауды береді.

2 мысалы . tgx=x теңдеуінің 0, 0001 дәлдігімен, Ньютон әдісі бойынша, ең кіші оң түбірін табу керек.

Шешуі: y =tgx және y=x қисықтарының графиктерін салып, ізделінді түбір ξπ<ξ<3π/2 интервалында жатқанында көреміз. Теңдеуді келесі түрге жазып алсақ, ƒ(x) ≡sinx-xcos x=0, төмендегіні аламыз .

ƒ’(x) =xsinx;

ƒ’’(x) =sinx+xcosx.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.