Көп айнымалылар функциялары: негізгі ұғымдар, шектер, дербес туындылар, дифференциалдар және экстремумдар


Көп айнымалылар функциясы.
Көп айнымалылар функциясы туралы негізгі ұғымдар мен шек.
1. Көп айнымалылардың функциялық тәуелділігі.
Табиғатта, практикада бір шаманың бір-біріне тәуелсіз басқа екі айнымалының өзгеруінен тәуелді болып келетіні жиі кездеседі.
Мысалы:
1. Тік төртбұрыштың ауданы z оның қабырғалары х пен у- тің өзгерісіне тәуелді, дәлдеп айтқанда:
z = х ∙ у .
Бұл жерде айнымалы z -пен басқа екі айнымалы х және у -тің арасындағы функциялық тәуелділікпен кездесіп отырмыз.
2. Физика курсында электр тогының күші I электр тізбегінің кернеуі V мен кедергі R-дің арасындағы байланыс Ом заңы бойынша
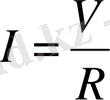
формуласымен өрнектелетіні белгілі. Сонымен ток күші І -дің шамасы кернеу V мен кедергі R-дің өзгерісіне тәуелді екенін, яғни айнымалы І -дің өзгерісі басқа айнымалы шама V мен R -дің өзгеруіне тәуелді екенін көреміз.
3. Егер жазықтықта орналасқан екі нүкте М 1 (х 1 , у 1 ), М 2 (х 2 , у 2 ) берілсе, онда ол нүктелердің ара қашықтығы
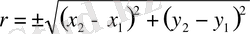
формуласымен анықталатыны аналитикалық геометриядан белгілі. Мұндағы айнымалы шама r басқа х 1 , х 2 , у 1 , у 2 төрт айнымалылардың (берілген нүктелердің координаталарының) өзгерісіне тәуелді.
Сөйтіп, бір айнымалының өзгерісі басқа екі, үш, төрт, онан да көп айнымалылардың өзгерісіне тәуелді болатынына көзіміз жетті. Міне осындай тәуелділіктерді бір айнымалының көп айнымалыларға функциялық тәуелділігі деп атаймыз.
Анықтама. Егер заң немесе ереже бойынша х пен у аргумент мәндерінің әрбір қос (пар) мәніне айнымалы z шамасынын бір мәні сәйкес қойылса, айнымалы z екі аргументтің функциясы деп аталады және бұл функция былай белгіленеді:
z = f(x, y),
немесе z =
 (х, у),
немесе z
= Ф(х, у),
(х, у),
немесе z
= Ф(х, у),
Нақты сандар х пен у-тің әрбір реттелген (х, у) пары тек қана бір А(х, у) нүктесіне сәйкес келетін болғандықтан, екі аргумент функциясының жоғарыда келтірілген жазылысын жазықтық нүктесінің функциясы түрінде де жазуға болады, яғни
z
=
f
(
A
), немесе
z
=
 (
A
), немесе
z
= Ф(
A
) .
(
A
), немесе
z
= Ф(
A
) .
Екі аргументгі функцияға мысалдар:
1.
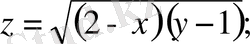 Equation. 3 (1)
Equation. 3 (1)
2.
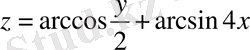 Equation. 3 (2)
Equation. 3 (2)
3. z = ln(7 x - y ) (3)
Анықтама. Егер аргументтер х пен у -тің нақты мәндерінен құрылған М= { х , у} жиынның құрамындағы әрбір (х, у) -ке сәйкес белгілі бір заң немесе ереже бойынша, сол аргументтердің функциясы z толық анықталған бір нақты мән қабылдаса, М жиыны екі аргументтің функциясы z-тің анықталу (бар болу облысы) деп аталады.
Келтірілген анықтаманы (1), (2), (3) мысалдардағы функциялардың бар болу облысын табу арқылы айқындалық.
Мысал. 1. z функциясының мәндері нақты сандар болып шығуы үшін
(2-х)
0 (4)
болуы шарт. Ал бұл теңсіздік төмендегі екі жағдайда ғана орындалады:
а)
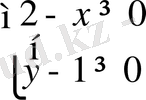 мұнан:
мұнан:
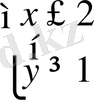 (5)
(5)
б)
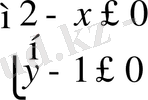 мұнан:
мұнан:
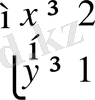 (6)
(6)
Демек, берілген (1) функцияның бар болу облысы х пен у аргументтерінің (5) және (6) арақатыстарды қанағаттандыратын нақты (х, у) қос мәндерінен құралған жиын болып шықты. (5) және (6) арақатыстарды қанағаттандыратын, яғни (1) функцияның бар болу облысын жасақтайтын нүктелерден құралған координаталық жазықтықтың бөлігі 1-сызбада көрсетілген.
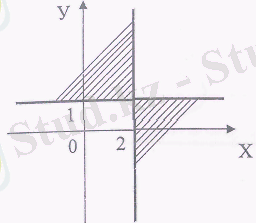
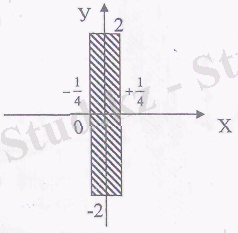
1-сызба 2-сызба
Мысал. 2. Арксинус пен арккосинус шамалары - 1-ден +1-ге дейін ғана өзгеретіні белгілі. Сол себепті
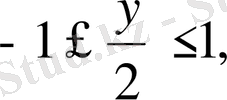 яғни - 2
яғни - 2
 у
у
 2 (7)
2 (7)
арақатыстары орындалады. Сонымен бірге:
-1
 4х
4х
 1, яғни
1, яғни
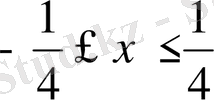 (8)
(8)
Демек, (2) функцияның бар болу облысы аргументтер х пен у-тің, (7) және (8) арақатыстарды қанағаттандыратын нақты пар мәндерінің жиыны болды.
Координаталық жазықтықтың (7) және (8) арақатыстарға сәйкес бөлігі 2-сызбада көрсетілген.
3. (3) логарифмдік функция нақты мәндерді тек
7х - у > 0, яғни у<7х (9)
болғанда ғана қабылдайды. Бұл теңсіздік берілген логарифмдік функцияның бар болу облысы координаталық жазықтығының 7х-у=0 түзуінен төмен жатқан бөлігі екенін дәлелдейді. Ол 3-сызбада көрсетілген.
4. Конустың көлемі z-ті оның жасаушысы х пен биіктігі у-тің функцнясы түрінде өрнектеу керек.
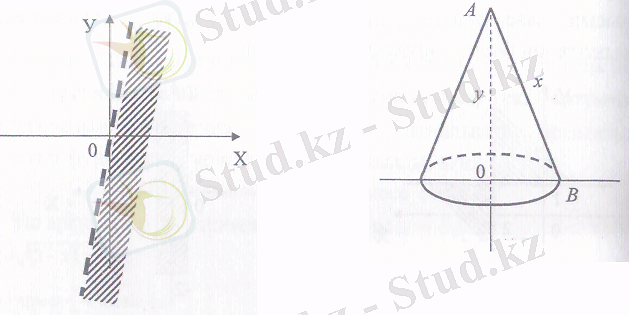
3-сызба 4-сызба
Берілген шарттарға сәйкес конус салынған (4-сызба), онда:
ОА=у, АВ=х. Конустың көлемі
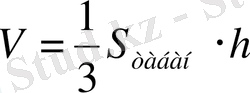
формуласы бойынша есептелетіні белгілі.
Ал біздің белгілеуімізде h
= у, V =z,
S
табан
=
 ∙ОВ
2
=
∙ОВ
2
=
 (х
2
-у
2
) .
(х
2
-у
2
) .
Демек,
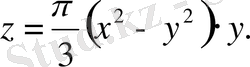
Егер қандай болса бір (х
0
, у
0
)
 М нүктесін алсақ, аргументтер х пен у-тің бұл мәндеріне z-тің толық анықталған мәні
z
0
=
f
0
(x
0
, y
0
) сәйкес келеді. Міне осы z
0
санын кеңістіктегі тік бұрышты координаталар системасындағы апликата деп алсақ, онда
В
0
(x
0
, у
0
, z
0
) = В
0
нүктесін салуға болады. Бұл процесті одан әрі соза берсек, кеңістікте
В
0
түріндегі нүктелердің жиынын да салып, шығамыз. Кеңістікте осылайша салынған нүктелердің жиыны екі аргументті функцияның графигін құрайды. Жалпы түрде екі аргументті функцияның графигі
z = f(x, y)
теңдеуімен берілген бет болып табылады.
М нүктесін алсақ, аргументтер х пен у-тің бұл мәндеріне z-тің толық анықталған мәні
z
0
=
f
0
(x
0
, y
0
) сәйкес келеді. Міне осы z
0
санын кеңістіктегі тік бұрышты координаталар системасындағы апликата деп алсақ, онда
В
0
(x
0
, у
0
, z
0
) = В
0
нүктесін салуға болады. Бұл процесті одан әрі соза берсек, кеңістікте
В
0
түріндегі нүктелердің жиынын да салып, шығамыз. Кеңістікте осылайша салынған нүктелердің жиыны екі аргументті функцияның графигін құрайды. Жалпы түрде екі аргументті функцияның графигі
z = f(x, y)
теңдеуімен берілген бет болып табылады.
Мысалдар.
1. z = 1 -x-y функциясының графигі (1; 0; 0), (0; 1; 0), (0; 0; 1) нүктелері арқылы өтетін жазықтық болады (5-сызба) .
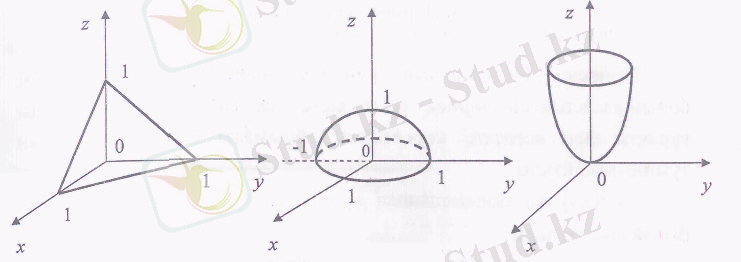
5-cызба 6-сызба 7-сызба
2.
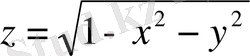 функциясының графигі центрі бас нүктеде, радиусы 1-ге тең болатын жарты сфера (6-сызба) .
функциясының графигі центрі бас нүктеде, радиусы 1-ге тең болатын жарты сфера (6-сызба) .
3. z = x 3 +у 2 функциясының графигі төбесі бас нүктеде болатын параболоид (7-сызба) .
2. Екі айнымалының функциясының үзіліссіздігі.
z = f(x, y) функциясы D облысында анықталсын. Осы облыстан М 0 (х 0 , у 0 ) нүктесін алып, оған сәйкес Δх және Δу өсімшелерін береміз, сонда алынған (х 0 +Δх; у 0 + Δ у) нүктесі де осы D облысына тиісті болуы керек.
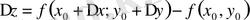 айырмасы
z = f(x, y)
функциясының (х
0
, у
0
) нүктесіндегі толық өсімшесі деп аталады.
айырмасы
z = f(x, y)
функциясының (х
0
, у
0
) нүктесіндегі толық өсімшесі деп аталады.
Бір айнымалынын функциясының үзіліссіздігі сияқты екі айнымалының функциясының үзіліссіздігін былай анықтаймыз.
Егер (х 0 , у 0 ) нүктесінде аргумент өсімшелері Δх, Δ у нольге ұмтылғанда оның толық өсімшесі Δz нольге ұмтылса, онда z=f(x, y) функциясы (х 0 , у 0 ) нүктесінде үзіліссіз деп аталады, яғни
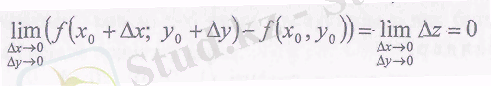
3. Дербес туындылар.
Бірнеше айнымалының функциясының берілген айнымалы бойынша алынған дербес туындысы деп басқа айнымалыларды тұрақты деп есептеп, көрсетілген айнымалы бойынша алынған туындыны айтады.
z = f(x, y) екі айнымалының функциясы үшін дербес туындылар былай анықталады:
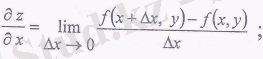
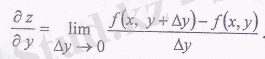
Дербес туындыларды түрінде белгілейді.
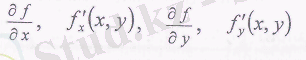
Мысалдар.
1. f(х 2, у) =х 2 +ху 2 +у 3 функциясыңың дербес туындысын тауып, онын Р 0 (1; 2) нүктесіндегі мәнін есептеу керек.
Шешуі:
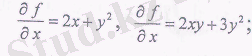
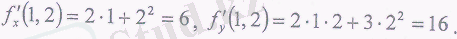
2. г = х -$ту функциясынын дербес туындыларын табу керек.
Шешуі:
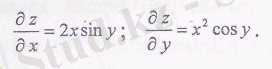
3. z=x y функциясының z' x , z' y дербес туындыларын табу керек.
Шешуі:
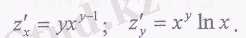
4. и = х 2 + у 2 + xtz 3 функциясының дербес туындыларын табу керек.
Шешуі:
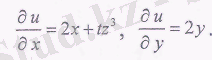
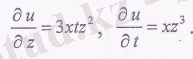
Бірнеше айнымалының функциясының дербес туындылары да бірнеше айнымалының функциясы болады. Сондықтан одан қайталап дербес туынды табуға болады. Берілген функцияға катысты бұл дербес туыңдылар жоғарғы ретті дербес туындылар деп аталады.
Мысалы, екі айнымалының функциясы үшін екінші ретті дербес туындылардың мынадай типтері бар:
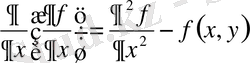 Equation. 3 функциясынан
х
аргументі бойынша екі рет алынған дербес туынды.
Equation. 3 функциясынан
х
аргументі бойынша екі рет алынған дербес туынды.
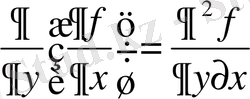 және
және
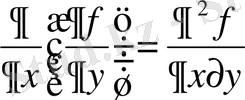 - аралас туындылар.
- аралас туындылар.
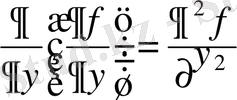 -f(x, y)
фунциясынан
y
аргументі бойынша екі рет алынған дербес туынды.
-f(x, y)
фунциясынан
y
аргументі бойынша екі рет алынған дербес туынды.
Теорема. Егер функциянын жоғарғы ретті туьтндылары үзіліссіз болса, онда оның айнымалылары бойынша дифференциалдауында ғана зйырмашылық болатын реті бірдей аралас туыңдылары тең болады.
Дербес жағдайда екі айнымалының функциясы үшін
М ы с а л.
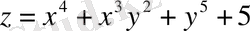 функциясының бірінші, екінші,
функциясының бірінші, екінші,
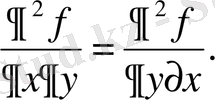 үшінші ретті дербес туьшдыларың табу керек. Шешуі:
үшінші ретті дербес туьшдыларың табу керек. Шешуі:
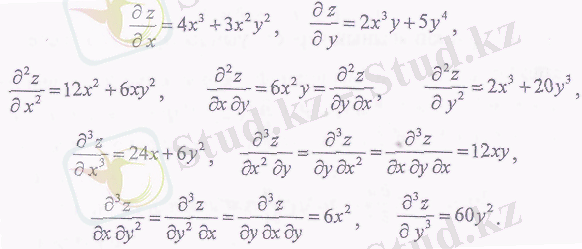
4. Екі айнымалының функцияеының дифференциалы.
z =
f(x, y)
функциясының
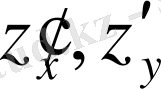 дербес туындылары үзіліссіз болсын.
дербес туындылары үзіліссіз болсын.
z' x ∙Δx көбейтіндісін z функциясының х айнымалысы бойынша алынған дербес дифференциалы деп атап, d х z = z' x ∙Δx немесе d x z = z' x ∙Δx символымен белгілейді, мұндағы dx = Δх- тәуелсіз айнымалы х-тің өсімшесі.
Дәл осылайша у айнымалы бойынша дербес дифференциалды анықтаймыз,
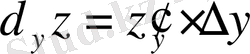 немесе
немесе
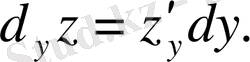
z функциясының дербес дифференішалдарының қосындысы оның толық дифференциалы деп атапып, dz символымен белгіленеді.
Сонымен.
dz = z' у dx + z' y dy .
Мысалы. z = (x + y) функциясының толык дифференциалын табу керек.
Шешуі: z' х = 2( x + y ), z' у =2(х+у) .
Сонда d z = 2(x + y) dx + 2(x + y) dy = 2(x + y) (dx + dy) .
5. Екі айнымалының функциясының экстремумы.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz