Лагранж интерполяциялық полиномы және оның қалдық мүшесі


Кіріспе
Күнделікті өмірде кездесетін көптеген ғылыми және техникалық есептерді шешу барысында бір функцияны басқа бір функциямен жуықтатуға тура келеді. Мұндай есептер әсіресе эксперимент нәтижесінде алынған сандарды өңдеу мәселелерімен тығыз байланысты. Мысалы, функция алдын ала белгісіз болып, оның дискреттік мәндері эксперимент арқылы функцияны жуықтатуға болады. Не болмаса функцияның аналитикалық түрі өте күрделі болса, онда оны есептеу үшін қарапайым функциямен алмастырылады.
Әдетте, жуықтаушы функцияны и н т е р п о л я ц и я л а у ш ы ф у н к ц и я деп аталады. Соңғы аталған функция көбінесе алгебралық полином болғандықтан, оны кейде интерполяциялаушы полином деп те аталады. Олар анықталған интегралдарды жуық шамамен есептеуде, дифференциялдық теңдеулердің шешімдерін табуда тағы сол сияқты кеңінен қолданылады.
Мен рефератымды « Интерполяциялаушы полином. Лагранждың интерполяциялық полиномы » атты тақырыбына жазамын.
Функцияны интерполяциялау есебінің қойылуы .
Айталық,
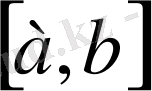 аралығының х
0
, х
1
, . . . , х
n
нүктесінде у = f (x) функциясының төмендегі мәндері берілген болсын:
аралығының х
0
, х
1
, . . . , х
n
нүктесінде у = f (x) функциясының төмендегі мәндері берілген болсын:
y о = f(x o ), y 1 = f(x 1 ), …, y n = f(x n )
Ерді осы
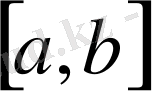 аралықтың
аралықтың
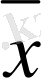
 x
i
нүктесінде y=f(x ) функциясының
x
i
нүктесінде y=f(x ) функциясының
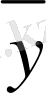 =f(
=f(
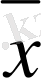 ) мәнін табу керек дейік ол үшін у=f(x) функциясы басқа, есептеуге оңай және белгілі бір мағынада оны жуықтайтын
) мәнін табу керек дейік ол үшін у=f(x) функциясы басқа, есептеуге оңай және белгілі бір мағынада оны жуықтайтын
 (x) интерполяциялаушы функциямен алмастырылады. Содан кейін
(x) интерполяциялаушы функциямен алмастырылады. Содан кейін
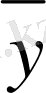 =f(x) мәнінің орнына y=f(x) функциясының сәйкес у
о
, у
1
, . . . , у
n
мәндері пайданылады.
=f(x) мәнінің орнына y=f(x) функциясының сәйкес у
о
, у
1
, . . . , у
n
мәндері пайданылады.
Әдетте, х о , х 1 , . . . , х n нүктелерін интерполяциялау тораптары , ал (х i , y i ) қос сандарын интерполяцияланудың берілгендері деп аталады.
Интерполяцияланушы
 (x) функциясы х
о
, х
1
, . . . , х
n
(x) функциясы х
о
, х
1
, . . . , х
n
 (х
i
) = f(х
i
) (
i =
0, 1, 2, …, n) 1. 1
(х
i
) = f(х
i
) (
i =
0, 1, 2, …, n) 1. 1
мәндерін қабылдап,
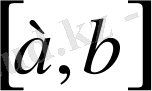 аралығының басқа нүктелерінде y=f(x) функциясына барынша жақын болуы тиіс. Сондағы негізгі мақсатымыз осындай шарттарды қанағаттандыратын функция құру. Осы есепті интерполяциялану деп атаймыз.
аралығының басқа нүктелерінде y=f(x) функциясына барынша жақын болуы тиіс. Сондағы негізгі мақсатымыз осындай шарттарды қанағаттандыратын функция құру. Осы есепті интерполяциялану деп атаймыз.
Бұл есепті шешу үшін, әуелі
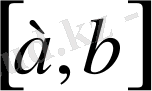 аралығында анықтылған, ал саны х
о
, х
1
, . . . , х
n
тораптардың санына тең.
аралығында анықтылған, ал саны х
о
, х
1
, . . . , х
n
тораптардың санына тең.
 о
(x)
о
(x)
 1
(x), …,
1
(x), …,
 n
(x)
n
(x)
Қарапайым сызвқтық тәуелсіз функциялар жүйесін таңдап аламыз. Содан кейін мына сызықтық комбинацияны құрамыз:
 (x) =
a
o
(x) =
a
o
 о
(x) +
a
1
о
(x) +
a
1
 1
(x) + …+
a
n
1
(x) + …+
a
n
 n
(x) =
n
(x) =
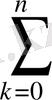 a
k
a
k
 k
(x)
k
(x)
Мұндағы a k коэффиценттері әзірше белгісіз сандар. Олар 1. 1 шартынан анықталады. Бұл шарттан a k коэффиценттерін табуға мүмкіндік беретін, теңдеулерінің саны (n+1) ге тең мынадай жүйе шығады:
a
o
 о
(x
о
) +
a
1
о
(x
о
) +
a
1
 1
(x
о
) + …+
a
n
1
(x
о
) + …+
a
n
 n
(x
о
) = f(x
o
)
n
(x
о
) = f(x
o
)
a
o
 о
(x
1
) +
a
1
о
(x
1
) +
a
1
 1
(x
1
) + …+
a
n
1
(x
1
) + …+
a
n
 n
(x
1
) = f(x
1
)
n
(x
1
) = f(x
1
)
1. 2
a
o
 о
(x
n
) +
a
1
о
(x
n
) +
a
1
 1
(x
n
) + …+
a
n
1
(x
n
) + …+
a
n
 n
(x
n
) = f(x
n
)
n
(x
n
) = f(x
n
)
Айталық, (1. 2) жүйесінің
∆=
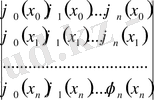 Equation. 3 1. 3
Equation. 3 1. 3
Анықтауышы ∆ (х 0 , х 1 , . . . , х n ) ≠ 0 болсын. Онда (1. 2) жүйесінің шешімдерін
a
o
=
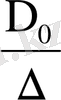 ,
a
1
=
,
a
1
=
 , …,
a
n
=
, …,
a
n
=
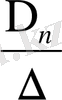
Крамер формуласы арқылы есептеуге болады. Мұндағы
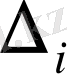 (
i =
0, 1, 2, …, n) анықтауыштары - ∆ анықтауышының
і
- тік жолын (у
о
, у
1
, . . . , у
n
)
(
i =
0, 1, 2, …, n) анықтауыштары - ∆ анықтауышының
і
- тік жолын (у
о
, у
1
, . . . , у
n
)
 векторымен алмастырғанда пайда болатын анықтаулштарға тең. Демек,
векторымен алмастырғанда пайда болатын анықтаулштарға тең. Демек,
 (x) =
(x) =
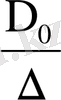
 о
(x) +
о
(x) +
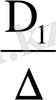
 1
(x) + . . . +
1
(x) + . . . +
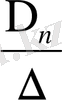
 n
(x) 1. 4
n
(x) 1. 4
Енді
 (
i =
0, 1, 2, …, n) анықтауышын
i
тік жолақтың
(
i =
0, 1, 2, …, n) анықтауышын
i
тік жолақтың
y о = f(x o ), y 1 = f(x 1 ), …, y n = f(x n )
Элементтері бойынша жіктейік сонда 1. 4 формуласы былайша жазылады.
 (x) = f(x
o
)
(x) = f(x
o
)
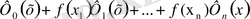 1. 5
1. 5
Мұндағы әрбір Ф
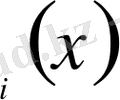 функцияны таңдап алынған
функцияны таңдап алынған
 о
(x)
о
(x)
 1
(x), …,
1
(x), …,
 n
(x) тәуелсіз функцияның сызықтық комбинацияларынан құралған функция 1. 5 теңдігіне х = x
i
(
i =
0, 1, 2, …, n) деп қарастырсақ, онда 1. 1 шарты орындалуы үшін Ф
n
(x) тәуелсіз функцияның сызықтық комбинацияларынан құралған функция 1. 5 теңдігіне х = x
i
(
i =
0, 1, 2, …, n) деп қарастырсақ, онда 1. 1 шарты орындалуы үшін Ф
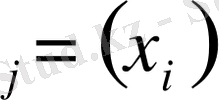 =0
=0
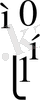
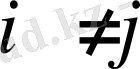 1. 6
1. 6
болуы керек
Ал енді ∆ (х
0
, х
1
, . . . , х
n
) ≠ 0 болғанда 1. 2 жүйесінің бір ғана шешімі бар. Сонымен бірге 1. 3 шарты
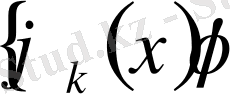 жүйесін тиісті түрде таңдап алғанда кез келген х
0
, х
1
, . . . , х
n
тораптары үшін орындалуы тиіс.
жүйесін тиісті түрде таңдап алғанда кез келген х
0
, х
1
, . . . , х
n
тораптары үшін орындалуы тиіс.
Егер 1. 3 шарты кез келген және бір- бірнеше теңсіздігі х
0
, х
1
, . . . , х
n
орындалатын болса, онда
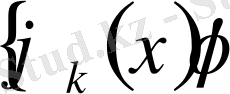 Чебышев жүйесі деп аталады.
Чебышев жүйесі деп аталады.
Мәселен,
1, х, х², . . . , х n
sinx, cosx, sin2x, cos2x, . . .
функциялары Чебышев жүйелерін құрайды.
Біз
 (x) алгебралық полином немесе сплайн интерполяциялық функция болатын жағдайда ғана қарастырамыз.
(x) алгебралық полином немесе сплайн интерполяциялық функция болатын жағдайда ғана қарастырамыз.
§2 Алгебралық полиномдар арқылы интерполяциялау.
2. 1 Лагранждың интерполяциялау полиномы .
Айталық,
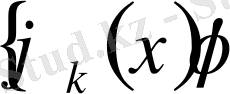 жүйесі
жүйесі
 о
(x) =1
о
(x) =1
 1
(x) =х
1
(x) =х
 2
(x) =х
2
, …,
2
(x) =х
2
, …,
 n
(x) =x
n
n
(x) =x
n
функциясынан құралған болсын . Бұл жағдайда
 (x) =
(x) =
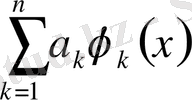
сызықтық комбинация n дәрежелі полином болады.
 (x) = Ln(x) =
(x) = Ln(x) =
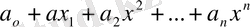
Онда 1. 2 жүйесі төмендегіше жазылады.
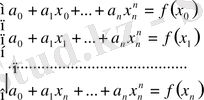 2. 1
2. 1
Бұл жүйенің
∆ (х
0
, х
1
, . . . , х
n
) =
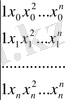 =П(х
k
-x
m
) ≠ 0 m ≥ k > n ≥ 0 анықтауышы- белгілі Вандерммонда анықтауышы. Оның мәні х
0
, х
1
, . . . , х
n
сандары әр түрлі болғанда 0 тең емес, яғни 2. 1 жүйесінің бір ғана шешімі бар. Демек, 1. 1 шартын қанағаттандыратын
=П(х
k
-x
m
) ≠ 0 m ≥ k > n ≥ 0 анықтауышы- белгілі Вандерммонда анықтауышы. Оның мәні х
0
, х
1
, . . . , х
n
сандары әр түрлі болғанда 0 тең емес, яғни 2. 1 жүйесінің бір ғана шешімі бар. Демек, 1. 1 шартын қанағаттандыратын
 (x) = Ln(x) =
(x) = Ln(x) =
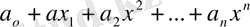 = f(x
o
)
= f(x
o
)
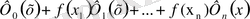 интерполяциялаушы алгебралық полином әр уақытта бар. Мұндағы Ф
к
(х)
интерполяциялаушы алгебралық полином әр уақытта бар. Мұндағы Ф
к
(х)
(k = 0, 1, 2, …, n) функциялары 1. 6 шартын қанағаттандыруы тиіс болатын. Ол үшін оларды мына түрде
Ф
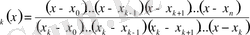
алса жеткілікті екенін дәлелдеу қиынға соқпайды.
Демек,
 (x) = Ln(x) =
(x) = Ln(x) =
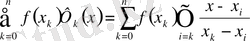 2. 2
2. 2
Әдетте (2. 2) полиномын Лагранждың интерполяциялық полиномы деп атайды. Келешекте
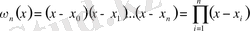
(n+1) - дәрежелі полиномын жиі пайдаланамыз. Ол полином үшін
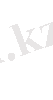
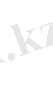
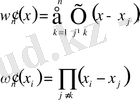
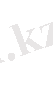 Сондықтан
Сондықтан
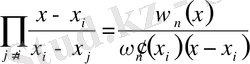
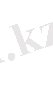
деп жазуға болады. Осы өрнектерді пайдаланып, Лагранж интерполяциялық басқаша түрде жазамыз:
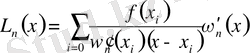 (2. 3)
(2. 3)
Мысал.
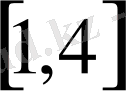 аралығының
аралығының
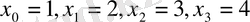
нүктелерінде
 мәндерін қабылдайтын
мәндерін қабылдайтын
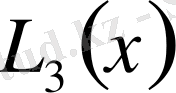 Лагранж интерполяциялық полиномын құру керек дейік.
Лагранж интерполяциялық полиномын құру керек дейік.
Ш е ш у і. Жоғарыдағы (2. 2) формуласы бойынша
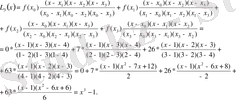
- Лагранждың интерполяциялық формуласы және оның қалдық мүшесі.
Айталық,
 аралығында y=f(x ) функциясының
аралығында y=f(x ) функциясының
 (к = 1, 2, . . . , n+1) үзіліссіз туындылары бар болсын. Осы ұйғарымды пайдаланып,
(к = 1, 2, . . . , n+1) үзіліссіз туындылары бар болсын. Осы ұйғарымды пайдаланып,
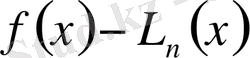
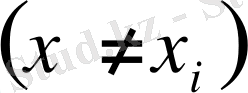 айырымын бағалаймыз. Құру бойынша
айырымын бағалаймыз. Құру бойынша
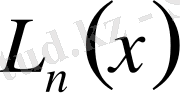 полиномы -
полиномы -
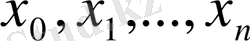 тораптары бойынша құрылған Лагранждың интерполяциялық полином. Олай болса
тораптары бойынша құрылған Лагранждың интерполяциялық полином. Олай болса
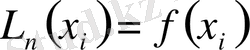
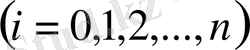 ал кез келген
ал кез келген
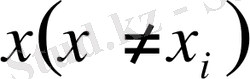 үшін жалпы жағдайда
үшін жалпы жағдайда
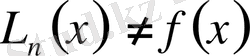 болады.
болады.
Мынадай
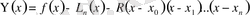
функциясын қарастырайық. Ол үшін
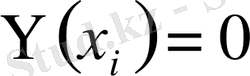

болатыны анық.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz