Кеңістіктегі координаталар әдісі мен векторлар: арақашықтық, кесінділерді бөлу және аффиндік түрлендірулер



Қазақстан Республикасы Білім және ғылым министірлігі
Оңтүстік Қазақстан Мемлекеттік Педагогикалық Институты
Кафедра: Физика - Математика
Тобы: 109-13 Математика
Қабылдаған: Жұмабаев М. Ж
Орындаған: Нематуллаев Хикматулла
Шымкент
2015 ж
Жоспар:
- Кеңістіктегі координаталар әдісі мен векторлар.
- Жалпы аффиндік және тікбұрышты координаталар жүйесі.
- Екі нүктенің ара қашықтығы.
- Кесіндіні берілген қатынаста бөлу.
Пайдаланған әдебиеттер
- Кеңістіктегі координаталар әдісі мен векторлар.
Кеңістікте үш координаталық ось өзара тікбұрыш жасап қиылысын. Олардың өлшем бірліктері (масштабтары) бірдей болсын. Олардың ортақ қиылысу нүктесін О - мен белгілеп координаталар басы деп атаймыз. Алынған жүйені кеңістіктегі тік Декарттық координаталар жүйесі деп атаймыз (1 - сызба) .
Бірінші координаталық осьті х әріпімен белгілейміз. Ох осі немесе абсцисса осі деп атаймыз.
Екінші координаталық осьті y әріпімен белгілейміз. Оy осі немесе ордината осі деп атаймыз.
Үшінші координаталық осьті z әріпімен белгілейміз. Оz осі немесе аппликата осі деп атаймыз.
Кеңісітіктегі тік Декартты координаталар жүйесі кеңістікті сегіз бөлікке бөледі. Оларды октанта деп атаймыз (2 -сызба) .
І октанта х > 0, y > 0, z > 0
ІІ октанта х < 0, y > 0, z > 0
ІІІ октанта х < 0, y < 0, z > 0
ІҮ октанта х > 0, y < 0, z > 0
Ү октанта х > 0, y > 0, z < 0
ҮІ октанта х < 0, y > 0, z < 0
ҮІІ октанта х < 0, y < 0, z < 0
ҮІІІ октанта х > 0, y < 0, z < 0
Кеңістікте кез- келген М (х, y, z) нүктесі берілсін. Ол жазықтық z осін бір нүктеде қияды. Ол нүктені Мz нүктесі деп белгілейміз. Тура сол сияқты М нүктесінен хОz және yОz осьтеріне параллель түзу жүргізейк. Олар сәйкесінше y осінен және х осінен Мy, Мz нүктесін қиып өтеді (3 сызба) . Онда ОМх, ОМy, ОМz шамаларын М нүктесінің кеңістіктегі тік Декарттық координатасы деп атаймыз және келесі символмен беогілейміз - М(х, y, z) . Мұндағы х = ОМх, y = ОМy, z = ОМz.
Кеңістіктегі тік Декарттық координаталар үшін М 1 (х 1 , y 1 , z 1 ) және М 2 (х 2 , y 2 , z 2 ) нүктелерінің арақашықтығы
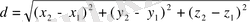 (1)
(1)
формуласымен анықталады.
Кеңістіктегі М 1 (х 1 , y 1 , z 1 ), М 2 (х 2 , y 2 , z 2 ), М 3 (х 3 , y 3 , z 3 ) нүктелері берілсін және М (х, y, z) нүктесі М 1 М 2 кесіндісін λ қатынасына бөлінсін, онда
λ = М 1 М / М М 2 - формуласымен анықталады. Соған байланысты М нүктесінінң координаталары мына формулалар арқылы анықталады:
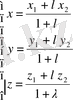 (2)
(2)
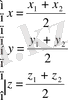 (3)
(3)
Кесіндіні берілген қатынастар бөлу формуласы.
Егер λ = 1 болса, онда кесінді қақ бөлінеді.
- Жалпы аффиндік және тікбұрышты координаталар жүйесі
Кез келген үш нүктенің коллинеарлық шарты сақталып, бір мәнді кеңістіктің нүкетлік түрленуі аффиндық түрлендіру деп аталады. Бұл түрлендіруде үш коллинеарлық нүкте үш коллинеарлық нүктелерге көшеді.
Аффиндық түрлендірудің негізгі қасиеті мынау: кеңістіктің кезе келген аффиндық түрленуі сызықтық түрленуге жатады. Аффиндық түрлендірудің қасиеттері мынадай:
- өз ара коллинеар болмайтын кеңістіктің үш нүктесі коллинеар емес үш нүктеге,
- өз ара компланар болмайтын төрт нүкте компланар емес төрт нүктеге,
- түзу сызық түзу сызыққа,
- қиылысатын екі түзу қиылысатын екі түзуге
- бір параллелограмның төрт төбесі екінші параллелограмның төрт төбесіне,
- бір кесіндінің ортасы екінші кесіндінің ортасына
- кеңістіктегі кез келген бір М нүктесі екінші бір М’нүктесінде көшеді. Бұл екі нүктенің әрқайсысы өзіне сәйкес координаталар системасында анықталады.
Егер осы айтылған қасиеттер сақталса, онда мұндай ұғымды аффиндік түрлендіру дейміз. Басқаша айтқанда, еркінше алынған аффиндік түрлендіруде сақталатын геометриялық бейнелердің қасиеттерін аффиндік түрлендіру дейміз. Мысалы, параллелограм, түзу сызық, эллипс, гипербола, парабола аффиндік ұғымға жатады. ал тік бұрышты төртбұрышты, шеңбер аффиндік ұғымға жатпайды. Өйткені аффиндік түрленуде тік бұрышты төртбұрыш параллелограмға ал шеңбер эллипске айналады. Сондықтан бұл екі пішін аффиндік ұғым болмайды. Сонымен түрлендірілгеннен кейін теореманың қасиеті сақталса, онда мұндай теорема аффиндік деп аталады. Мысалы, үш медиана бір нүктеде қиылысады деген теорема аффиндік болады, ал үш биссектриса бір нүктеде қиылысады деген теорема аффиндік теоремаға жатпайды. Аффиндік ұғымдар мен теоремалардың жиындысын аффиндік геометрия деуге болады. Аффиндік геометрияда кесіндінің ұзындығы деген ұғым жоқ. Мұнда кез келген кесіндіні координаталық вектор деп қабылдауға болады. Аффиндік түрленудегі координаталық вектор ұзындығы еркінше алынатын кез келген вектор болуы мүмкін. Осы сияқты аффиндік геометрияда аудан мен көлем де анықталмайды.
Енді аффиндік түрлендірудің қандай болатынын мысалдар арқылы қарастырайық. Бір жазықтықтың бойындағы шексіз алыстағы нүктелерге осы жазықтықпен үйлесетін екінші жазықтықтың бойындағы шексіз алыстағы нүктелер сәйкес болса, онда жазықтықтағы нүктелердің аффиндік түрленуі деп коллинеарлық түрлендіруді айтамыз.
Үш түзудің теңдеулерін біртектес координаталар арқылы алайық:
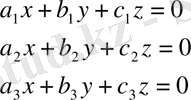 (8)
(8)
Бізге бір түзудің бойында жатқан екі түрлі координаталар берілсін, яғни
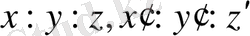 . Бұлар бір координаталар системасындағы
. Бұлар бір координаталар системасындағы
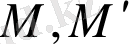 екі нүктені анықтасын. Егер
екі нүктені анықтасын. Егер
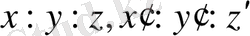 координаталарының кейбір мәндерінде мынадай теңдік орындалса
координаталарының кейбір мәндерінде мынадай теңдік орындалса
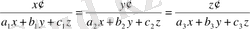 (9)
(9)
Онда бұл теңдеу коллинеарлық түрленуді көрсететін теңдеу деп аталады. Өйткені бір түзудің бойындағы нүкте түрленгеннен кейін сол түзудің бойындағы екінші нүктеге көшеді, яғни түзу түзуге көшеді. Мұндай коллинеарлық түрленуде қасиеттері сақталатын
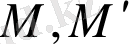 нүктелерінің координаталары өз ара пропорционал болады:
нүктелерінің координаталары өз ара пропорционал болады:
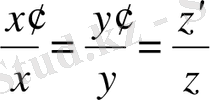
Ендеше
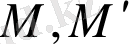 нүктелерін анықтау үшін мынадай теңдеулерді аламыз:
нүктелерін анықтау үшін мынадай теңдеулерді аламыз:
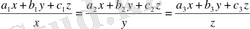 (10)
(10)
Осыдан
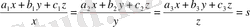
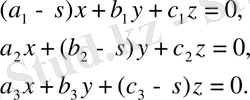 (11)
(11)
(11) теңдеулер системасы шешілу үшін бұлардың коэффициентерінен құрылған үшінші ретті анықтауыш нольге тең болу керек:
а 1 - s b 1 c 1 (12)
а 2 b 2 - s c 1
а 3 b 3 c 3 - s
Бұл - s параметріне қарағанда үшінші дәрежелі теңдеу, яғни үш теңдеудің түбіріне сәйкес келетін үш нүкте берілген коллинеарлық түрлендіруді көрсетеді. Шындығында, бұл түрленуде үш нүкте өзгерілмей сақталып отырады, олар - инвариант нүктелер, дербес жағдайда өз ара үйлеседі немесе жорымал болады.
Осы берілген коллинеарлық түрленуде сақталатын түзулер қозғалмайтын екі нүктелерді қосқаннан шығады. Өйткені бұл нүктелер инварианттар, ал осы екі нүктені қосатын түзу өзіне көшетін түзу болады. Аффиндік немесе декарттық координаталар арқылы мынадай теңдеулерді жазайық:
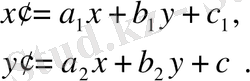 (13)
(13)
Егер мұндағы анықтауыш нольге тең болмаса, яғни
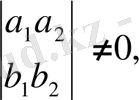
Онда аффиндік түрлену (13) бір мәнді болады. Аффиндік түрленуде бірінші жазықтықтың әрбір түзуі екінші жазықтықтың әрбір түзуіне көшеді, яғни бір түзудің бойында жатқан нүктелерге екінші түзудің бойындағы нүктелер сәйкес келеді. Мына y=kx түзуінің бойындағы шексіз алыстағы нүктелерге коэффициенті
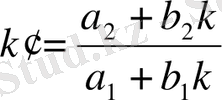
Шамасына тең түзудің бойындағы шексіз алыстағы нүктелерге сәйкес келеді. Басқаша айтқанда түзу түзуге көшеді. Бұдан мынадай қорытынды шығады: параллель түзулер шексіз алыста қиылысатын болғандықтан, олар аффиндік түрленуде параллель түзулерге көшеді.
(13) теңдеуді біртектес координаталар арқылы алайық:
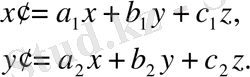
Мұның аффиндік түрленуі мынадай болады:
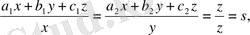 (13)
’
(13)
’
Осыдан мынадай теңдеулер системасы шығады:
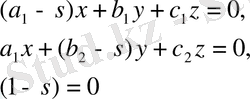 (14)
(14)
Бұл теңдеулер системасы шешілу үшін мына үшінші ретті анықтауыш нольге тең болу керек:
а 1 - s b 1 c 1 (14 ’ )
а 2 b 2 - s c 1 =0.
а 3 b 3 c 3 - s
осындай үшінші дәрежелі теңдеудің бір түбірі бірге тең (s 1 =1), ал қалған екі s 2, s 3 түбірлері нақты немесе жорымал болуы мүмкін. Егер үшінші дәрежелі теңдеудің барлық түбірлері әр түрлі болса, онда, онда аффиндік түрлендірудің үш инвариант нүктелері бар, оның біреуі шекті қашықтықта ал қалған екі нүктесі шексіз алыста, нақты немесе жорымал болады. Осы нүктелерге сәйкес өз ара инвариант болатын үш түзу шығады.
Аффиндік түрлендіруде бір жазықтықта жатқан түзудің бойындағы М 1, М 2, М 3 үш нүктенің М 1 М 3 : М 3 М 2 қатынасы аффиндік түрлендірудің инварианты болады. Осының дұрыс екендігін көрсету үшін мынадай қатынасты қарастырайық:
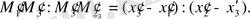
Формула бойынша
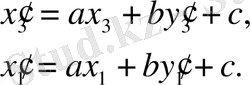
Бірінші теңдеуден екінші теңдеуді алсақ, мынадай болады:
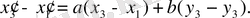
Осы сияқты
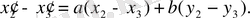
Соңғы екі теңдіктің қатынасын түрлендіріп табайық:
(15)
Сөйтіп, аффиндік түрленуде түзудің бойындағы кез келген М
1
, М
2
, М
3
үш нүктеге сол түзудің бойындағы үш нүкте
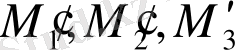 сәйкес келеді:
сәйкес келеді:
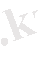
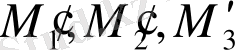
Немесе
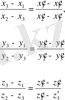 (15
’
)
(15
’
)
Бір тік бұрышты декаттық координаталар системасынан екінші тік бұрышты декарттық координаталар системасыа көшу аффиндік системасының дербес түрленуіне жатады. Мысалы:
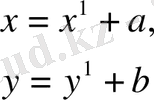 Немесе
Немесе
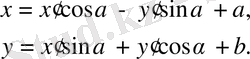
Бұл формулалардың негізгі мағынасы мынау: бір жазықтықтағы М нүктесі екінші жазықтықтағы М нүктесіне әрқашанда сәйкес келеді, яғни екі жазықтықтың бетінде жатқан екі нүкте бір-біріне бір мәнді сәйкес келеді. Осы шарт орындалғанда бір жазықтық екінші жазықтыққа түрленеді дейміз. Бұл жагдайда бір жазықтықтың бойындағы бір пішінге екінші жазықтықтың бойындағы белгілі бір пішін сәйкес болып отырады. Мәселен, F және F пішіндері-екі жазықты беттестіргеннен шыққан пішіндер, ал екеуі өз ара сәйкес келеді. Мұндай F, F пішіндері конгруэнттік пішіндер деп аталады. Ал олардың бір-біріне сійкес көші конгруненттік түрлену деп аталады. Сондықтан жоғарғы жазылған
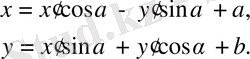
Формулаларды конгруэнттік түрлендіруді сипаттайды. Осы сияқты кеңістіктегі аффиндік түрлендіру мынадай формулалармен сипатталады:
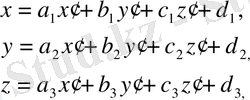 (16)
(16)
Мұндағы
a 1 b 1 c 1
a 2 b 2 c 2
a 3 b 3 c 3
Ортогональдық матрица, d 1 , d 2, d 3 - кез келген сандар, М (х, у, z),
М (х ’ , у ’ , z’, ) - координаталар системасына сәйкес нүктелер.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz