Нормаланған сызықтық кеңістіктің түйіндес кеңістігі мен түйіндес операторлары


Кіріспе3
1 Сызықтық кеңістікке түйіндес кеңістік4
1. 1. Түйіндес кеңістік4
1. 2 Сызықтық нормаланған кеңістіктегі әлсіз жинактылық. 6
2 Сызықтық нормаланған кеңістікке түйіндес кеңістіктер8
2. 1 . Түйіндес кеңістіктер8
2. 2 Түйіндес кеңістіктің мысалдары10
Қорытынды15
Пайдаланған әдебиеттер16
Кіріспе
Анықтама 1
.
Егер әрбір
 нақты сан мәнді
нақты сан мәнді
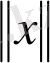 функциясы анықталса және ол мына шарттарды қанағаттандыратын болса:
функциясы анықталса және ол мына шарттарды қанағаттандыратын болса:
1)
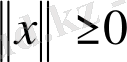 және тек
және тек
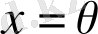 болғанда ғана
болғанда ғана
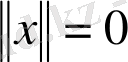 (норманың теріс еместік шарты) ;
(норманың теріс еместік шарты) ;
2) кез келген
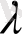 саны үшін
саны үшін
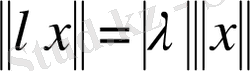 (норманың біртектілік шарты) ;
(норманың біртектілік шарты) ;
3) кез келген
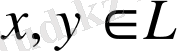 үшін
үшін
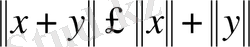 ( үшбұрыш теңсіздігі), онда
( үшбұрыш теңсіздігі), онда
 кеңістігінде
норма
анықталған дейміз.
кеңістігінде
норма
анықталған дейміз.
Жұмыстың мақсаты. Анықтамада келтірілген 1), 2), 3) шаттары норманың аксиомалары деп аталады. Норма анықталған сызықтық кеңістік нормаланған сызықтық кеңістік деп аталады.
Анықтама 2.
 нормаланған сызықтық кеңістігінде анықталған сызықтық функционалдардың
нормаланған сызықтық кеңістігінде анықталған сызықтық функционалдардың
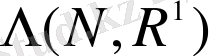 сызықтық кеңістігі
сызықтық кеңістігі
 кеңістігіне түйіндес кеңістік
деп аталады.
кеңістігіне түйіндес кеңістік
деп аталады.
 кеңістігіне түйіндес
кеңістігіне түйіндес
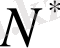 символымен таңбалаймыз. Анықтама бойынша, бұл кеңістіктің кез келген
символымен таңбалаймыз. Анықтама бойынша, бұл кеңістіктің кез келген
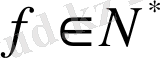 элементі (сызықтық функционал) үшін оның нормасы жоғарыда
элементі (сызықтық функционал) үшін оның нормасы жоғарыда
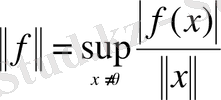 теңдігімен анықталады және ол норманың аксиомаларын қанағаттандыратыны айқындалды. Сондықтан
теңдігімен анықталады және ол норманың аксиомаларын қанағаттандыратыны айқындалды. Сондықтан
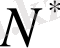 - нормаланған сызықтық кеңістік.
- нормаланған сызықтық кеңістік.
Теорема.
Түйіндес кеңістік
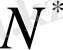 әрқашан толық кеңістік.
әрқашан толық кеңістік.
Дәлелдеуі
.
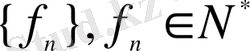 тізбегі фундаменталь тізбек болсын: кез келген
тізбегі фундаменталь тізбек болсын: кез келген
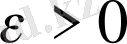 берілгенде барлық
берілгенде барлық
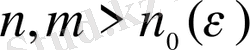 нөмірдері үшін
нөмірдері үшін
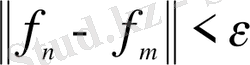 (4) теңсіздігі орындалатындай
(4) теңсіздігі орындалатындай
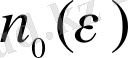 саны табылатын болсын. Норманың анықтамасы бойынша (4) теңсіздігінің салдары ретінде
саны табылатын болсын. Норманың анықтамасы бойынша (4) теңсіздігінің салдары ретінде
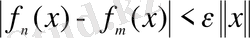 (5) теңсіздігі
(5) теңсіздігі
 кеңістігіндегі әрбір
кеңістігіндегі әрбір
 үшін орындалады және
үшін орындалады және
 тұрақты, ал
тұрақты, ал
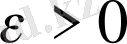 кез келген сан болғандықтан, (5) теңсіздігі
кез келген сан болғандықтан, (5) теңсіздігі
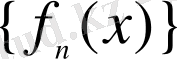 сандар тізбегі үшін Коши критерийі орындалатынын
сандар тізбегі үшін Коши критерийі орындалатынын
Жұмыстың міндеттері:
- Түйіндес кеңістіктің болатынын дәлелдеуді;
- Түйіндес кеңістігінің негізгі мысалдарын;
1 Сызықтық кеңістікке түйіндес кеңістік Түйіндес кеңістікАнықтама.
нормаланған сызықтық кеңістігінде анықталған сызықтық функционалдардың
сызықтық кеңістігі
кеңістігіне түйіндес кеңістік деп аталады.
 кеңістігіне түйіндес кеңістікті
кеңістігіне түйіндес кеңістікті
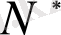 символымен таңбалаймыз. Анықтама бойынша, бұл кеңістіктің кез-келген
символымен таңбалаймыз. Анықтама бойынша, бұл кеңістіктің кез-келген
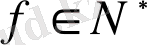 элементі (сызықтық функционал) үшін оның нормасы жоғарыда
элементі (сызықтық функционал) үшін оның нормасы жоғарыда
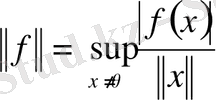 (1)
(1)
Теңдігімен анықталды және ол норманың аксиомаларын қанағаттандыратыны айқындалды. Сондыктан
- нормаланған сызықтық кеңістік.
Мысал үшін
кеңістігіне түйіндес
кеңістігін айқындайық. Сол мақсатпен алдын ала,
кеңістігінде анықталған кез-келген сызықтық функционал
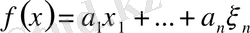 (2)
(2)
Түрінде болатынын дәлелдейік.
( Сонымен,
осы кеңістіктегі кез-келген сызықтық функционал, ал
векторлары осы кеңістікте базис болсын. Онда кез-келген
векторы
түрінде жіктеледі. Бұл теңдікке сызықтық функционалды қолданып
теңдігіне келеміз. Енді функционалдың базистік векторлардағы мәндерін
, деп таңбаласак, функционал (2) түріне келеді. Кеңістіктің әр векторы берілген базис бойынша бірмәнді жіктелетін болғандыктан
сандары базис бойынша бірмәнді анықталады. Сондыктан (2)
кеңістігіндегі сызықтық функционалдың жалпы түрі деп аталады.
(2) теңдігінін оң жағында тұрған
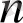 айнымалылы сызықтық функция, ол коэффициенттері,
айнымалылы сызықтық функция, ол коэффициенттері,
 сандары, берілсе, толық анықталады. Бұл сандарды
сандары, берілсе, толық анықталады. Бұл сандарды
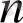 - өлшемді
- өлшемді
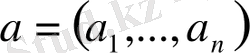 векторының координаттары ретінде қарастыруға болады. Басқаша айтқанда,
векторының координаттары ретінде қарастыруға болады. Басқаша айтқанда,
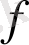 функционалы
функционалы
 векторы берілуімен толық анықталады. Сондықтан
векторы берілуімен толық анықталады. Сондықтан
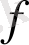 функционалы мен оны анықтаушы
функционалы мен оны анықтаушы
 векторы ажыратылмай, бір
векторы ажыратылмай, бір
Нәрсе түрінде қабылданады. Демек,
функционалы дегеніміз
векторы. Ал
, сондықтан мұндай векторлардың жиыны
кеңістігін кұрады, яғни
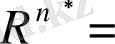
.
Бірінші қарастырған мысалымызда түйіндес кеңістік бастапқы кеңістіктің өзі болды, яғни
- өзіне өзі түйіндес кеңістік. Бірақ кейін бұл жағдай тек кейбір кеңістіктерге ғана тән екенін көреміз.
Ескерту.
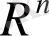 кеңістігіндегі сызықтық функционалдың жалпы түрін айқындайтын (2) теңдігін тұрақты
кеңістігіндегі сызықтық функционалдың жалпы түрін айқындайтын (2) теңдігін тұрақты
 векторы мен айнымалы
векторы мен айнымалы
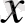 векторының скаляр көбейтіндісі түрінде, яғни
векторының скаляр көбейтіндісі түрінде, яғни
, (3)
түрінде де қарастыруға болатынына зер аударайык.
Қарастырылған мысалдан нормаланған сызықтық
кеңістігіне түйіндес
кеңістігін айқындау үшін
кеңістігіндегі сызықтық функционалдың жалпы түрін білу қажет екені байқалды. Осыған байланысты (1. 2) пунктінде келтірілген мысалдардағы негізгі кеңістіктерге түйіндес кеңістіктер кейін V-тарауда айқындалады.
Енді түйіндес кеңістіктің бір жалпы қасиеті туралы мына тұжырымды келтірейік.
Теорема. Түйіндес кеңістік
әрқашан толық кеңістік.
Дәлелдеуі.
тізбегі фундаменталь тізбек болсын: кез-келген
берілгенде барлық
нөмірлері үшін
( 4)
теңсіздігі орындалатындай
саны табылатын болсын. Норманың анықтамасы бойынша (4) теңсіздігінің салдары ретінде
(5)
теңсіздігі
 кеңістігіндегі әрбір
кеңістігіндегі әрбір
 үшін орындалады және
үшін орындалады және
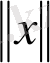 тұрақты, ал
тұрақты, ал
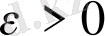 кез-келген сан болғандықтан, (5) теңсіздігі
кез-келген сан болғандықтан, (5) теңсіздігі
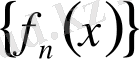 сандар тізбегі үшін Коши критерийі орындалатынын көрсетіп тұр. Демек, бұл тізбектің шегі бар, оны
сандар тізбегі үшін Коши критерийі орындалатынын көрсетіп тұр. Демек, бұл тізбектің шегі бар, оны
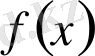 арқылы белгілейік. Сызықтық функционалдардың шегі
арқылы белгілейік. Сызықтық функционалдардың шегі
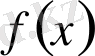 функционалы да сызықтық қасиетті сақтайды. Шынында да,
функционалы да сызықтық қасиетті сақтайды. Шынында да,
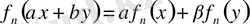 себебі
себебі
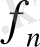 - сызықтық функционал. Осы теңдікте шекке көшіп,
- сызықтық функционал. Осы теңдікте шекке көшіп,
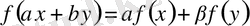 теңдігін аламыз, демек
теңдігін аламыз, демек
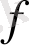 - сызықтық функционал. Сандар тізбегінің (5) теңсіздігінде
- сызықтық функционал. Сандар тізбегінің (5) теңсіздігінде
 кезде шекке көшіп,
кезде шекке көшіп,
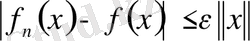 (6)
(6)
Теңсіздігіне келеміз. Осы теңсіздіктен
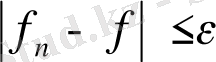
Яғни
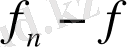 шенелген функционал екендігі шығады. Енді
шенелген функционал екендігі шығады. Енді
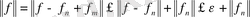 ,
,
ал
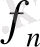 шенелген функционал болғандықтан, бұл теңсіздіктен
шенелген функционал болғандықтан, бұл теңсіздіктен
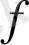 функционалының шенелгендігін көреміз, демек ол үздіксіз функционал. Қорытып айтқанда,
функционалының шенелгендігін көреміз, демек ол үздіксіз функционал. Қорытып айтқанда,
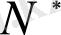 кеңістігіндегі шенелген функционалдардың
кеңістігіндегі шенелген функционалдардың
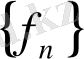 фундаменталь тізбегінің шегі
фундаменталь тізбегінің шегі
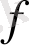 бар және ол шенелген сызықтық функционал болатыны, яғни
бар және ол шенелген сызықтық функционал болатыны, яғни
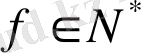 екені дәлелденді. Демек,
екені дәлелденді. Демек,
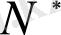 толық кеңістік. Теорема дәлелденді.
толық кеңістік. Теорема дәлелденді.
Енді түйіндес кеңістікке байланысты тізбек жинақтылығының басқа бір анықтамасын беруге болады.
Анықтама.
 - нормаланған сызықтық кеңістік, ал
- нормаланған сызықтық кеңістік, ал
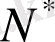 - оған түйіндес кеңістік болсын. Сондай-ақ,
- оған түйіндес кеңістік болсын. Сондай-ақ,
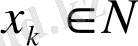 элементтердің тізбегі, ал
элементтердің тізбегі, ал
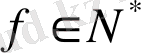 кез-келген функционал болсын. Егер
кез-келген функционал болсын. Егер
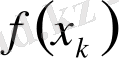 сандарының тізбегі барлық
сандарының тізбегі барлық
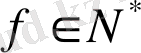 үшін
үшін
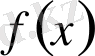 санына жинақты болса, онда
санына жинақты болса, онда
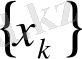 тізбегі
тізбегі
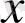 элементіне әлсіз жинақталады дейміз.
элементіне әлсіз жинақталады дейміз.
2 Сызықтық нормаланған кеңістікке түйіндес кеңістіктер 2. 1 . Түйіндес кеңістіктерҚысқаша: Егер
үшін
кезде
болса, онда әлсіз мағынада
дейміз.
Әлсіз жинақтылықтан ажырату үшін бұрын анықталған норма бойынша жинақтылықты әлді жинақтылық деп атаймыз. Басқаша айтқанда, егер
болса, онда әлді мағынада
дейміз.
Егер тізбек әлді жинақты болса, онда ол тізбек әлсіз жинақты болады. Шынында да, егер
болса, онда
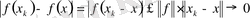
Демек,
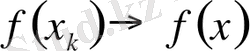
Ескерту. Кері тұжырым әрқашан дұрыс бола бермейді. Жалпы жағдайда әлсіз жинақты тізбек әлді жинақталмауы мүмкін.
Сонымен қатар,
кеңістігінде кері тұжырым да дұрыс, басқаша айтқанда, бұл кеңістікте әлді және әлсіз мағынадағы жинақтылық пара-пар.
Мысалдар.
Анықтама 1
.
Егер әрбір
 нақты сан мәнді
нақты сан мәнді
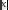 функциясы анықталса және ол мына шарттарды қанағаттандыратын болса:
функциясы анықталса және ол мына шарттарды қанағаттандыратын болса:
1)
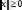 және тек
және тек
 болғанда ғана
болғанда ғана
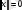 (норманың теріс еместік шарты) ;
(норманың теріс еместік шарты) ;
2) кез келген
 саны үшін
саны үшін
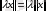 (норманың біртектілік шарты) ;
(норманың біртектілік шарты) ;
3) кез келген
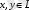 үшін
үшін
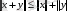 ( үшбұрыш теңсіздігі), онда
( үшбұрыш теңсіздігі), онда
 кеңістігінде
норма
анықталған дейміз.
кеңістігінде
норма
анықталған дейміз.
Анықтамада келтірілген 1), 2), 3) шаттары норманың аксиомалары деп аталады. Норма анықталған сызықтық кеңістік нормаланған сызықтық кеңістік деп аталады.
Анықтама 2.
 нормаланған сызықтық кеңістігінде анықталған сызықтық функционалдардың
нормаланған сызықтық кеңістігінде анықталған сызықтық функционалдардың
 сызықтық кеңістігі
кеңістігіне түйіндес кеңістік
деп аталады. кеңістігіне түйіндес
сызықтық кеңістігі
кеңістігіне түйіндес кеңістік
деп аталады. кеңістігіне түйіндес
 символымен таңбалаймыз. Анықтама бойынша, бұл кеңістіктің кез келген
символымен таңбалаймыз. Анықтама бойынша, бұл кеңістіктің кез келген
 элементі (сызықтық функционал) үшін оның нормасы жоғарыда
элементі (сызықтық функционал) үшін оның нормасы жоғарыда
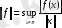 теңдігімен анықталады және ол норманың аксиомаларын қанағаттандыратыны айқындалды. Сондықтан - нормаланған сызықтық кеңістік.
теңдігімен анықталады және ол норманың аксиомаларын қанағаттандыратыны айқындалды. Сондықтан - нормаланған сызықтық кеңістік.
Теорема.
Түйіндес кеңістік
 әрқашан толық кеңістік.
әрқашан толық кеңістік.
Дәлелдеуі
.
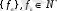 тізбегі фундаменталь тізбек болсын: кез келген
тізбегі фундаменталь тізбек болсын: кез келген
 берілгенде барлық
берілгенде барлық
 нөмірдері үшін
нөмірдері үшін
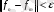 (4) теңсіздігі орындалатындай
(4) теңсіздігі орындалатындай
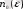 саны табылатын болсын. Норманың анықтамасы бойынша (4) теңсіздігінің салдары ретінде
саны табылатын болсын. Норманың анықтамасы бойынша (4) теңсіздігінің салдары ретінде
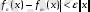 (5) теңсіздігі кеңістігіндегі әрбір
(5) теңсіздігі кеңістігіндегі әрбір
 үшін орындалады және
үшін орындалады және
 тұрақты, ал кез келген сан болғандықтан, (5) теңсіздігі
тұрақты, ал кез келген сан болғандықтан, (5) теңсіздігі
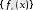 сандар тізбегі үшін Коши критерийі орындалатынын
сандар тізбегі үшін Коши критерийі орындалатынын
көрсетіп тұр. Демек, бұл тізбектің шегі бар, оны
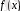 арқылы белгілейік. Сызықтық функционалдардың шегі функционалы да сызықтық қасиетті сақтайды. Шынында да,
арқылы белгілейік. Сызықтық функционалдардың шегі функционалы да сызықтық қасиетті сақтайды. Шынында да,
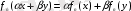 , себебі
, себебі
 сызықтық функционал. Осы теңдікте шекке көшіп,
сызықтық функционал. Осы теңдікте шекке көшіп,
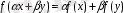 теңдігін аламыз, демек
теңдігін аламыз, демек
 сызықтық функционал. Сандар тізбегінің (5) теңсіздігінде
сызықтық функционал. Сандар тізбегінің (5) теңсіздігінде
 кезде шекке көшіп,
кезде шекке көшіп,
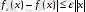 (6) теңсіздігіне келеміз. Осы теңсіздіктен
(6) теңсіздігіне келеміз. Осы теңсіздіктен
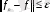 (7), яғни
(7), яғни
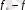 шенелген функционал екендігі шығады. Енді
шенелген функционал екендігі шығады. Енді
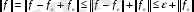 , ал
, ал
 шенелген функционал болғандықтан, бұл теңсіздіктен
шенелген функционал болғандықтан, бұл теңсіздіктен
 функционалының шенелгендігін көреміз, демек ол үздіксіз функционал. Қорытып айтқанда, кеңістігіндегі шенелген функционалдың
функционалының шенелгендігін көреміз, демек ол үздіксіз функционал. Қорытып айтқанда, кеңістігіндегі шенелген функционалдың
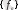 фундаменталь тізбегінің шегі бар және ол шенелген сызықтық функционал болатыны яғни
фундаменталь тізбегінің шегі бар және ол шенелген сызықтық функционал болатыны яғни
 екені дәлелденді. Демек, толық кеңістік. Теорема дәлелденді.
екені дәлелденді. Демек, толық кеңістік. Теорема дәлелденді.
Мысал үшін
 кеңістігіне түйіндес
кеңістігіне түйіндес
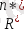 кеңістігін айқындайық. Сол мақсатпен, алдын ала, кеңістігінде анықталған кез келген сызықтық функционал
кеңістігін айқындайық. Сол мақсатпен, алдын ала, кеңістігінде анықталған кез келген сызықтық функционал
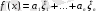 (2) түрінде болатынын дәлелдейік. Сонымен, осы кеңістіктегі кез келген сызықтық функционал, ал
(2) түрінде болатынын дәлелдейік. Сонымен, осы кеңістіктегі кез келген сызықтық функционал, ал
 векторлары осы кеңістікте базис болсын. Онда кез келген
векторлары осы кеңістікте базис болсын. Онда кез келген
 векторы
векторы
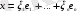 түрінде жіктеледі. Бұл теңдікке сызықтық функционалды қолданып
түрінде жіктеледі. Бұл теңдікке сызықтық функционалды қолданып
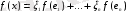 теңдігіне келеміз. Енді функционал базистік векторлардағы мәндерін
теңдігіне келеміз. Енді функционал базистік векторлардағы мәндерін
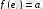 деп таңбаласақ, функционал (2) түріне келеді. Кеңістіктің әр векторы берілген базис бойынша бірмәнді жіктелетін болғандықтан
деп таңбаласақ, функционал (2) түріне келеді. Кеңістіктің әр векторы берілген базис бойынша бірмәнді жіктелетін болғандықтан
 сандары базис бойынша бірмәнді анықталады. Сондықтан (2) кеңістігіндегі сызықтық функционалдың жалпы түрі деп аталады. (2) теңдігінің оң жағында тұрған
сандары базис бойынша бірмәнді анықталады. Сондықтан (2) кеңістігіндегі сызықтық функционалдың жалпы түрі деп аталады. (2) теңдігінің оң жағында тұрған
 айнымалылы сызықтық функция, ол коэфициенттері,
айнымалылы сызықтық функция, ол коэфициенттері,
 сандары, берілсе, толық анықталады. Бұл сандарды
сандары, берілсе, толық анықталады. Бұл сандарды
 өлшемді
өлшемді
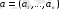 векторының координаттары ретінде қарастыруға болады.
векторының координаттары ретінде қарастыруға болады.
Басқаша айтқанда, функционалы
 векторы берілуімен толық анықталады. Сондықтан функционалы мен оны анықтаушы векторы ажыратылмай, бір нәрсе түрінде қабылданады. Демек, функционалы дегеніміз векторы. Ал
векторы берілуімен толық анықталады. Сондықтан функционалы мен оны анықтаушы векторы ажыратылмай, бір нәрсе түрінде қабылданады. Демек, функционалы дегеніміз векторы. Ал
 , сондықтан мұндай векторлардың жиыны кеңістігін құрады, яғни
, сондықтан мұндай векторлардың жиыны кеңістігін құрады, яғни
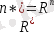 .
.
Сызықты
Е
кеңістігінде анықталған барлық сызықты функционалдар жиыны өз кезегінде сызықты кеңістік болады (дәлелдеңіздер) . Бұл кеңістік берілген кеңістікке түйіндес кеңістік деп аталады да,
 деп белгіленеді.
деп белгіленеді.
Сонымен,
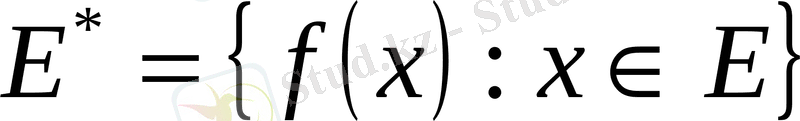 , мұндғы
, мұндғы
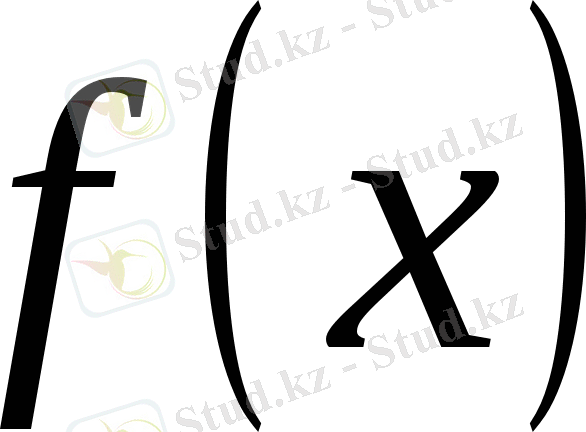 -
Е
кеңістігінде анықталған сызықты функционал
.
-
Е
кеңістігінде анықталған сызықты функционал
.
Түйіндес кеңістіктегі норма:
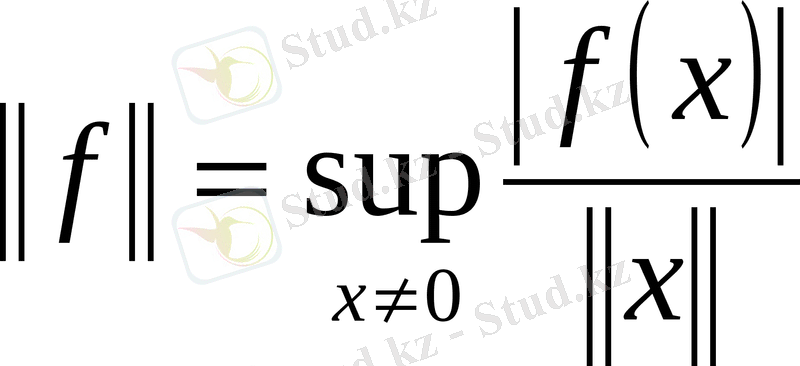 немесе
немесе
 . Сонымен, түйіндес кеңістіктік - нормаланған сызықты кеңістік.
. Сонымен, түйіндес кеңістіктік - нормаланған сызықты кеңістік.
Түйіндес кеңістіктегі әлді топология - осы кеңістіктегі топология бойынша жинақтылық.
Теорема 1.
Түйіндес кеңістік
 әрқашан толық.
әрқашан толық.
Түйіндес кеңістіктің мысалдары.
- кеңістігіндегі функционалдың жалпы түрі.
кеңістігіндегі сызықты функционалды
деп алайық.
Сызықты функционалдың анықтамасы бойынша,
.
, деп белгілеп алсақ,
болады. Енді
шарттарын қанағаттандыратын сызықты функционалддары үшін
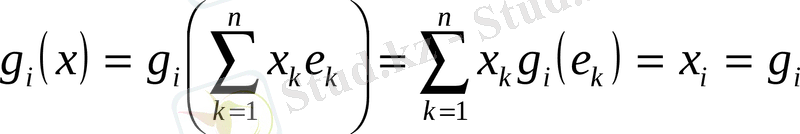
теңдіктері орындалатынын ескеріп,функционалын
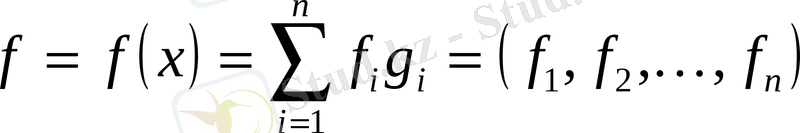
түріне келтіремізде оның нормасын анықтаймыз. Осы мақсатпен,үшін
.
теңсіздігінен төмендегі сұлбаға келеміз:
. (*)
Осымен қатар,элементі
және
теңдіктері орындалатынын ескеріп,
болатынын көреміз. Демек, (*) теңсіздігінде
элементе теңдік орындалатынын көркміз. Сондықтан,
болады.
Сонымен біз-ге түйіндес
кеңістігіне келеміз. Яғни,
өлшемді евклид кецістігіне түйіндес кеңістік
өлшемді евклид кецістігі болады.
2. 3 Түйіндес операторлар
... жалғасы2.
дегі әрбір
функциясына
функциясына сәйкес қоятын t операторын құрайық. Бұл оператор өзі түйіндес екеніне көз жеткізу қиын емес.
Бұдан әрі «шектеулі» деген сөзді біз қалдырып кетеміз. Алдыңғыдан, егер t - өзі түйіндес оператор және α-нақты сан болса, онда αt-да өзі түйіндес оператор, және егер t мен u - өзі түйіндес операторлар болса, онда u+t - өзі түйіндес, ал tu сонда, тек сонда ғана өзі түйіндес, егер t мен u операторы ауыстырымды болса. Ең соңында, егер
бірқалыпты немесе күшті операорлық топология мағынасында жинақты болса, онда t-да өзі түйіндес оператор болады.
Егер
ті х бойынша және у бойынша функционал болса, мұнда t - өзі түйіндес оператор, онда біз
деп белгілейтін осы функционал келесі шарттарды қанағаттандыратын көру қиын емес:
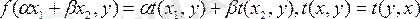
Ондай функционалды біз бисызықты Эрмит формасы деп атаймыз. Бұл форма
мағынасында шектеулі, мұнда С t - кейбір тұрақты (қарастырған жағдайда
) .
Сонымен, әрбір өзі түйіндес t операторы кейбір шектеулі бисызықты
Эрмит формасын тудырады.
Керісінше, егер шектеулі бисызықты
Эрмит формасы берілсе, онда ол
теңдігін қанағаттандыратын кейбір өзі түйіндес t операторын тудырады.
Іс жүзінде,
формасында у элементін белгілеп, біз х-тен сызықтық функционал аламыз. Сонымен
мұнда у / элементі бірмәнді анықталады. Сонда, біз
теңдігімен анықталатын және
болатындай t операторын аламыз. t - сызықтық оператор екені айқын. t - шектеулі оператор екеніне оңай көз жеткізуге болады. Расында да
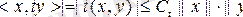
деп және
ке қысқартып
екенін табамыз. t - өзі түйіндес оператор екенін көрсетеміз. Кез келген
үшін
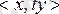
бұдан
және
екені шығады.
Енді бисызықты
Эрмит формасын аламыз және онда
делік. Барлық х-тер үшін нақты мәндер алып
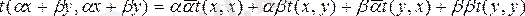
болатындай
квадрат формасын аламыз. Сондай
формасын
бисызықты Эрмит формасына сәйкес квадраттық Эрмит формасы деп атаймыз. Егер
бисызықты Эрмит формасы берілсе, онда сол арқылы сәйкес квадраттық
Эрмит формасы беріледі. Кері жағдай да ақиқат, квдарттық
Эрмит формасы берілуі бисызықты
Эрмит формасын бірмәнді анықтайды. Бұл бисызықты форма келесі теңдікпен анықталады (полярлау принципі)
(3)
мұнда
және
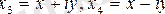
Квадраттық Эрмит формасы
сонда, тек сонда ғана шектеулі болады, яғни
егер сәйкес бисызықты форма шектеулі болса ғана екенін көрсету қиын емес.
формасы
үшін полярлық деп аталады.
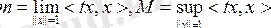
болсын делік.
m және М сандары өзі түйіндес t операторының төменгі және жоғарғы шекарасы деп аталады.
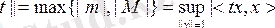
екенін көрсетейік.
Іс жүзінде,
болсын делік. Сонда
(4)
және сондықтан
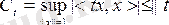
Басқа жағынан, кез келген
үшін
болады. Сондықтан, егер z Н-тағы нөлден ерекше элемент болса, онда
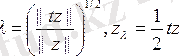
деп
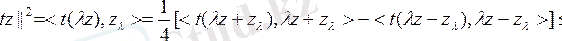
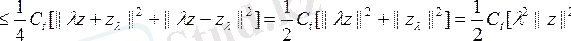
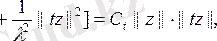
екенін аламыз, бұдан
және содан
(5)
(4) және (5) теңсіздіктерінен керекті теңдікті аламыз. Дәлелденген бойынша, жеке жағдайда, егер барлық
үшін өзі түйіндес t мен u операторлары
теңдігі орындалса, онда

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz