Хаусдорф теоремасы

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 13 бет
Таңдаулыға:

ТАКЫРЫБЫ: Хаусдорф теоремасы МАЗМҰНЫ

Кіріспе3

1 Толық метрикалық кеңістік5

1. 1 Толық метрикалық кеңістіктегі Е жиыны Теорема 15

1. 2 Теорема 2. компакт жиыны7

2 Хаусдорф теоремасы9

2. 1 Хаусдорф теоремасы немесе парадоксы9

2. 2 Теореманы дәлелдеу10

Қорытынды12

Пайдаланған әдебиеттер13

Кіріспе

Сызықты нормаланған метрикалық кеңістіктегі компактылық. Бұл тақырыптағы негізгі мәселе метрикалық кеңістіктегі жиындардың компакт немесе шалакомпакакт болу критерийлерін игеру. Осымен қатар, жеке метрикалық кеңістіктегі жиынның компакт болу шарттарын игеру.

Жұмыстың мақсаты. Жиынның метрикалық кеңістіктегегі компакт болу белгісі - Хаусдорф теоремасы. Бұл жалпылама теореманы жеке қарастырылатын метрикалық кеңістікте қолдану көптеген қиын мәселелерді шешуді керек қылады. Сондықтан жекелеген метрикалық кеңістікте қолдануға қолайлы критерилер қалаптасқан. Мысалы кеңістігіндегі жиын компакт болуы үшін оның шенеулі болуы жеткілікті.

Алдын ала кейбір қарапайым ұғымдардың метрикалық кеңістіктегі анықтамасын еске салайық. X- кез-келген метрикалық кеңістік болсын.

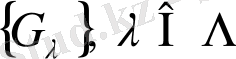Анықтама 1. кез-келген жиын және , ашық жиындардың кез-келген үйірі болсын. Мұнда 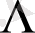индекс 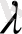мәндерін қабылдайтын сандар жиыны. Жалпы жағдайда ол саналымсыз жиын болуы мүмкін. Егер 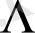саналымды жиын болса, онда 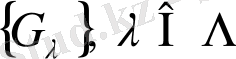, жиындар тізбегі, ал жалпы жағдайда жиындар үйірі болады.

Егер кез-келген элементі , жиындарының ең болмағанда бірінде жататын болса, онда , үйірі А жиынын бүркейді дейміз.

Анықтама 2. жиынының барлық элементтерін қамтитын радиусы ақырлы шар бар болса, онда А шенелген жиын деп аталады.

Басқаша айтқанда, қайсыбір элементі мен саны үшін болса, онда А шенелген жиын болғаны.

Бұл тұжырымдар метрикалық кеңістігінде де орындалады. Бірақ өлшемі ақырсыз кеңістіктерге бұл принциптерді бүлжытпай таратуға болмайды екен. Компакт жиын ұғымы - осы тұжырымдардың жалпы метрикалық кеңістік тұрғысыңдағы бірегей жалпыламасы.

Анықтама 3. Егер метрикалъқ кеңістіктегі А жиынының кез - келген ақырсыз ішжиынында жинақты тізбек бар болса, онда А шала компакт жиын деп аталады. Ал осындай тізбектің шегі А жиынында жатса, онда А компакт жиын деп аталады.

Бұл анықтамадан компакт жиын тұйық жиын, сондай-ақ, шала компакт жиынның тұйыктауы компакт жиын екені көрінеді. Дербес жағдайда, егер А компакт тізбек болса, оның жинақты іштізбегі бар болады.

Кеністік анықталған X жиыны компакт жиын болса, онда бұл метрикалық кеңістік компакт деп аталады.

Жалпы метрикалық кеңістіктердегі жиынның (шала) компакт болуының критерийін келтірер алдында -тор ұғымының анықтамасын берейік.

Жұмыстың міндеттері:

шенелген және жете шенелген жиындар ұғымын;

- метрикалық кеңістіктегі жиынның компакт болу шартын (Хаусдорф теоремасын) .

- шала компактылық критериін;

- жекелеген метрикалық кеңістіктегі жиынның компактылық шарттарын;

- Арцел теоремасын;

- ақырлы өлшемді кеңістіктегі жиынның компакт болу шартын.

1 Толық метрикалық кеңістік 1. 1 Толық метрикалық кеңістіктегі Е жиыны Теорема 1

Х метрикалық кеңістік, ал және осы кеңістіктегі жиындар болсын. Егер кез-келген саны және кез-келген элементі үшін теңсіздігі орындалатын элементі табылатын болса, онда Т жиыны Е жиыны үшін - тор болады дейміз.

Е жиыны үшін 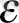-тор болатын Т жиыны Е жиынында жатуы міндет емес. Мысалы, кеңістігінде бүтін сандар жиыны нақты сандар жиыны үшін 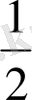-тор болады. Сондай-ақ, иррационал сандар жиыны үшін де жиыны 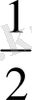-тор болады. Бірінші жолы тор құрайтын жиын нақты сандар жиынының құрамында жатыр, ал екінші жолы ол иррационал сандар жиынынан тысқары жатыр. Әрине, Т жиынының бөлігі Е жиынында болып, қалғандары сыртыңда болуы да, Т жиыны Е жиынында түгелімен жатуы да мүмкін.

Енді метрикалық кеңістіктегі жиынның компакт жиын болуының критерийін беретін теореманы дэлелдейік.

Теорема 1 (Ф. Хаусдорф) . Толық метрикалық кеңістіктегі Е жиыны үшін кез-келген үшін ақырлы -тор бар болуы Е жиыны шала компакт жиын болуының қажетті жеткілікті шарты.

Шарттың қажеттілігі. Е - (шала) компакт жиын болсын. Кез келген үшін Е жиынының -тор болатын, саны ақырлы Т жиыны табылатынын дәлелдейік. Е жиынының кез-келген нүктесін алып, шартына сай нүктесін іздейік. Егер бұл шарт орындалатын нүкте табылмаса, онда Е жиынының барлық нүктелері үшін теңсіздігі орындалатын болғаны. Демек, Е жиыны үшін тек нүктесі -тор болғаны.

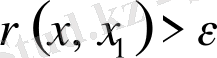
Ал, шартына сай нүктесі бар болса, онда және шарттарына сай нүктесін іздейміз. Егер бұл шарттар орындалатын нүкте табылмаса, онда жиыны Е үшін -тор болғаны. Басқа жағдайда осы екі шартты қанағаттандыратын нүктесі табылады . . . Бұл әрекет қайсыбір -нші ретте, нүктелері табылғаннан кейін, тоқталады. Шынында да, егер ол шексіз созыла берсе, онда Е жиынының элементтерінен тұратын тізбегі пайда болар еді және мұндағы кез-келген екі элементтің арақашықтығы болар еді. Бірақ бұл тізбек жинақсыз және мұнда жинақты іштізбек те жоқ екені 3-анықтама алдында келтірілген мысалдағы байыптауға ұқсас дәлелденеді. Ал, бұл жағдай Е жиынының компактылылығы туралы теорема шартына қайшы. Демек, Е жиыны үшін -тор болатын ақырлы жиын табылады.

Шарттың жеткіліктілігі. Е жиынының ақырсыз ішжиынында жинақты тізбек бар екенін дәлелдейік. Шарт бойынша Е жиыны үшін ақырлы -тор кез-келген үшін табылады. Осыған сәйкес, үшін Е жиынының ақырлы -торы жиыны болсын. Радиусы 1-ге тең, центрлері нүктелерінде орналасқан тұйық шарларының бірігуі Е жиынын толық қамтиды. Шынында да, кез-келген үшін және нүктелерінің ең болмаса біреуі үшін , демек . Сонымен, . А жиыны ақырсыз болғандыктан, осы шарлардың ең болмағанда бірінде оның ақырсыз бөлігі бар. Сол ішжиынды арқылы, ал оны қамтып жатқан шарды арқылы белгілейік.

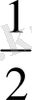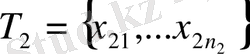Енді Е жиынының -торы жиыны болсын. Радиусы 1/2-ге тең, центрлері 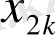нүктелерінде орналасқан 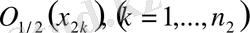тұйық шарларының бірігуі Е жиынын толық қамтиды. Осы шарлардың ең болмаса бірінің 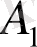жиынымен қиылысуы 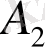- ақырсыз жиыны болады. Оны қамтып жатқан шарларды 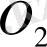арқылы белгілейік. Сонда, 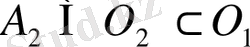. Осы әрекетті әрі қарай шексіз қайталау нәтижесінде 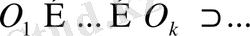тұйық шарлар тізбегі, сонымен қатар 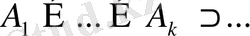ақырсыз жиындар тізбегі

пайда болады. Мұнда 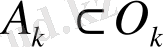және 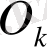шарының радиусы 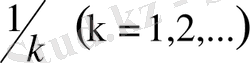. Біріне бірі еніп жатқан тұйық шарлар тізбегі туралы теорема бойынша осы шарлардың бәріне тиісті бір ғана 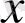нүктесі бар, яғни 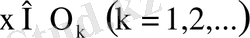. . Енді әр 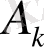жиынынан бір 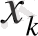нүктесін алайық. Онда 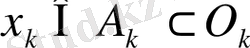демек, 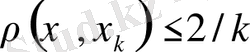,, яғни 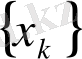тізбегі кезде нүктесіне жинақталады. Ақырында, 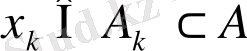, демек кез-келген ақырсыз жиынында жинақты тізбек бар екені айқындалды.

Осымен теорема толық дәлелденді.

Ескерту. Егер Е жиыны үшін кез-келген санына сәйкес ақырлы -тор бар болса, онда Е жиыны, әдетте, жете шенелген жиын деп аталады.

Компакт жиын ұғымы, екінші жағынан, жоғарыда айтылған ақырлы бүркеме туралы (Гейне-Борель леммасы) тұжырымды да жалпылайды. Оны келесі теоремадан көреміз.

1. 2 Теорема 2. компакт жиыны

Теорема 2. компакт жиын болу үшін Е жиының, ашьқ жиындармен кез-келген бүркеуінен саны ақырлы бүркеуді бөліп алуға болатындығы қажетті және жеткілікті шарт.

Дәлелденген теоремалар жалпы метрикалық жағдайында дәлелденгендіктен, олардың шарттары жеке тексеруге ыңғайлы бола бермейді. Бірақ, әдетте, тұжырымдарды пайдаланып, жеке кеңістіктер үшін қолдануға ыңғайлы критерилер алынады. Сондай қритерийлердің бір көрнекті мысалы кеңістігіндегі функциялар жиынының компактылығының критерийін тұжырымдайтын Арцела теоремасын қарастырайық.

Алдымен үздіксіз функциялар жиындарына тән ұғымдарға тоқталайық.

кеңістігінде үздіксіз функциялардың жиыны берілген болсын. Мысалы, А жиыны функцияларынық параметріне тәуелді үйірі болсын. Параметр өзінің мәндерін қайсыбір (саналымды, не саналымсыз) жиынынан қабылдайды.

Анықтама 5. Егер қайсыбір К саны үшін теңсіздігі барлық және үшін орындалса, онда жиыны (үйірі) бірқалыпты шенелген дейміз.

Мысалы, үйірі барлық және мәндері үшін теңсіздігін қанағаттандыратыны айқын. Демек, бұл аралығында бірқалыпты шенелген функциялардың үйірі.

Келесі анықтаманы беру алдында математикалық анализ курсынан белгілі тағы бір ұғымды еске алайық. Ол функциянь берілген жиында, мысалы кесіндісінде, біркалыпты үздіксіздігі. Келесі анықтама үйірдегі барлық функцияларды бірқалыпты үзіліссіздігі бір шенде болуын талап етеді.

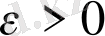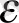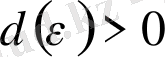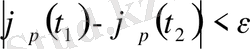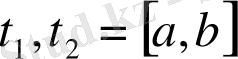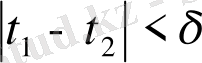Анықтама 6. Егер кез-келген үшін - нен ғана тәуелді табылып теңсіздігі және шарттарына сай барлық нүктелерде және параметрдің барлық мәндері үшін орындалса, онда 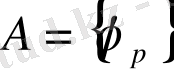функциялар үйірін біршенде үздіксіз деп атаймыз.

Бүл анықтама бойынша функциялар жиыны біршенде болу үшін, саны тек берілген санына ғана тәуелді, бірақ нүктелері мен параметріне тәуелсіз табылуы шарт.

2 Хаусдорф теоремасы 2. 1 Хаусдорф теоремасы немесе парадоксы

Хаусдорф теоремасы (немесе парадоксы ) - көпшілік теориясында дәлелденген қабылданған Т есептік жиынтықтың S ² екі өлшемді саласының, 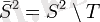$\bar S^2=S^2\setminus T$ қосымша болатын, үш бірдей бірін- бірі кесіп өтпейтін 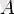, 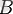және С жиынтық түрінде көрсетілуі мүмкін және бір -біріне салыстыруға және 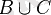$B\cup C$ жиынтығына. Ең алғашқы рет Ф. Хаусдорф 1914 жылы жариялаған. Бұл теорема ( осының негізінде кейіннен құрылған Банах- Тарскийдің теоремасы) әдеттегі геометриялық тәжірибедегі ( 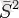$\bar S^2$ екі көшірмесін алты бөлікке бөліп, одан 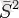$\bar S^2$ үш көшірмесін құрастыруға болатындығын айтады) теориялық-жиынтықтық сәйкессіздіктерді көрсетеді. Сондықтан кейде «парадокс» деп айтылады.

Теореманы дәлеледеуде таңдау аксиомасын пайдаланады. Бұл аксиоманы басқада баламалармен ауыстыру, Хаусдорф теоремасын теріске шығарып дәлелдейді (бұл, тиісті салаларын бөлуге мүмкіндігі болып табылады ) .

Теоремадан, екі өлшемді салада соңғы қосымша өлшемі, басқа жиынтықтармен тең мән беретін конгруенттік жиынтықтар болмайтындығы көрінеді( яғни сферадағы қозғалыстың салыстырмалы нұсқасы)

Кейде «Хаусдорф парадоксы» деп осы теорема дәлелденген мақаладағы басқа теоремамен шатастырады. Бұл теорема Витали жиынтығына ұқсас мысал келтіреді. Бұл теорема бірлік кесіндіні жұп бөліктерге бөлуге және тек бір ғана қозғаудың көмегімен екі кесіндінің ұзындығын құрауға болатындығын айтады. Бұл барлық жиынтықтарда түзудің шегі жоқ екендігін көрсетеді. Бірақ шектеулі жиынтықтар жазықтығында (түзуде) жіктік жиынтықтар тең шек болатын соңғы -аддитивтік шегін анықтауға болады.

2. 2 Теореманы дәлелдеу

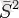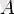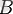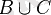
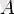Мұнда теореманың жеңілдетілген нұсқасын дәлелдейміз. Дәлірек, бөлінген сфераның тесілген жұп жиынтық нүктелерінің (оны $\bar S^2$ деп атайық) үш жұп конгруенттік бөліктер , және , $B\cup C$ жиынтығына конгруентті екендігін (оны 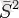$\bar S^2$ деп атайық) дәлелдейміз. Бұл пікір, Хаусдорф теоремасы секілді екі өлшемді сферада барлық жиынтықта болатындай және қозғалыста өзгермейтіндей «ауданын» анықтауға болмайтындығын көрсетеді.