Анықтауыштарды есептеу, кері матрица, матрица рангі және меншік мәндер мен векторлар: әдістер мен қасиеттер


Анықтауыштар және оларды есептеу
Кез келген n-реттегі А шаршы матрицаға, бір заңдылықпен, осы матрицаның n-реттегі анықтауышы немесе детерминанты деген атпен бір сан сәйкестендіріледі. Екінші және ушінші реттегі анықтауыштан бастайық.
Мына a 11 , a 12 және a 21, a 22 төрт санынан тұратын
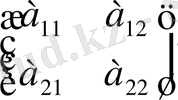
кесте берілген болсын. Бұл кесте (матрица) екінші ретті деп аталады. Өйткені оның жол саны мен бағана саны өзара тең және ол екіге тең. Сонымен(1. 16) кестеге (матрицаға) сәйкес келетін екінші ретті анықтауыш (детерминант) деп (а 11 а 22 -а 12 а 21 ) санын айтады да, оны мына символмен:
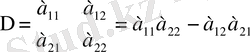
бейнелейді. Бұл жерде ескере кететін бір жай - матрица реті туралы ұғым тек оның жол саны мен тік бағана сандары тең болған жағдайда ғана айтылады. Ал оның жол саны мен бағана саны өзара тең болмаса, онда матрица мөлшері ретті емес деп есептелінеді.
Мысал.
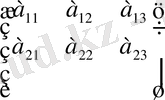
матрицасы екі жолдан және үш бағанадан тұратын болғандықтан, оның көлемі 2x3 мөлшерлі матрицаның ғана анықтауышы болатынын көреміз.
Сонымен жоғарыдағы (1. 17) анықтауыш екінші ретті анықтауыш деп аталады. Себебі оның жол және бағана сандары екіге тең.
Үшінші және одан жоғары ретті анықтауыштар да осы екінші ретті анықтауышқа ұқсас түрде анықталады. Сондықтан да үшінші ретті анықтауыш үш жолдан және үш бағанадан тұрады:
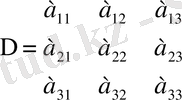 .
.
Сол сияқты төртінші ретті анықтауыш төрт жолдан және төрт бағанадан тұратын болады:
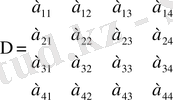 .
.
Осы сияқты онан әрі n-ретті анықтауыш n жолдан және n бағанадан тұрады.
Сонымен анықтауыштың реті оның жолдар саны мен бағана санының теңдігіне байланысты. Олай болса екінші ретті анықтауышта 2 2 =4 элемент, үшінші ретті анықтауышта 3 2 =9 элемент, осы сияқты n-ретті анықтауышты n 2 - элемент болатындықтарын көреміз.
Енді осы анықтауыштарды қалай есептеп табуға болатындығына тоқталайық.
Біз екінші ретті анықтауыштың анықтамасын бергенде, оның қалай есептелетьіндігін де бірден көрсетіп кеттік. Осыған байланысты тағы мына бір жағдайды да бұдан былай қарай есте ұстаған жөн: (1. 16) анықтауыштың сол жақтағы жоғарғы бұрышынан оң жақтағы төменгі бұрышына қарай ойша жүргізілген сызықтық осы анықтауыштың бас диагоналі деп аталады. Осыдан барып екінші ретті анықтауыштың мәні оның бас диагоналінің бойында жатқан элементтердің көбетіндісінен оның жанама диагоналінің бойында жатқан элементтердің көбейтіндісін шегеріп тастағанда шығатын санға тең екенін білеміз.
Ал енді үшінші ретті анықтауыштың мәнін есептеп шығару үшін Саррюс ережесі деп аталатын ереже қолданылады. Осы ережеге тоқталайық. Үшінші ретті анықтауыштың алдыңғы екі жолын оның төменгі жағына түсіріп жазайық. Сонда төмендегідей №1-сызба келіп шығады. Енді осы сызбаның үстіндегі берілген анықтауыштың бас диагоналінің бойындағы үш элементтің көбейтіндісін а 11 а 22 а 33 және оған екі параллельдің бойындағы үш элементтердің көбейтінділерін а 21 а 32 а 13 , және а 31 а 12 а 23 оң таңбамен, ал теріс таңбамен -а 13 а 22 а 31 , -а 23 а 32 а 11 , -а 33 а 12 а 21 аламыз.
Осылай алынған алты мүшенің алгебралық қосындысын берілген үшінші ретті анықтауыштың мәні деп атайды. Үшінші ретті анықтауышты осылай есептеуді Саррюс ережесі деп атайды.
Сонымен
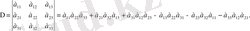
Мысал.
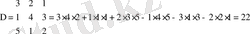
Сонымен матрицалардың барлық түрлерінің ішінде тек шаршы матрицаның ғана анықтауышы болады және ол
 немесе det
A
, немесе
немесе det
A
, немесе
 түрінде жазылады.
түрінде жазылады.
Анықтауыштың қасиеттері
1-қасиет. Анықтауыштың жатық жолдарын сәйкес тік жолдарымен алмастырғаннан, яғни транспонерлегеннен анықтауыш мәні өзгермейді:
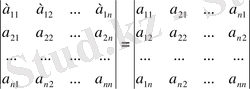
Теңдіктің дұрыстығын анықтауыштарды есептеу арқылы тексеруге болады.
2-қасиет. Анықтауыштың қандай да бір жолының ортақ көбейткішін анықтауыш алдына шығаруға болады. Үшінші ретті анықтауыштың екінші жолындағы ортақ көбейтішті анықтауыш алдына шығарамыз.
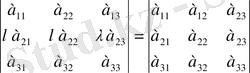
3-қасиет. Анықтауыштың екі жолының орнын ауыстырғанна анықтауыш таңбасы қарама-қарсы таңбаға өзгереді. Үшінші ретті анықтауыштың бірінші және екінші жолдарын алмастырайық:

4-қасиет. Егер анықтауыштың екі жолы бірдей болса, онда анықтауыш мәні нөлге тең. Үшінші ретті анықтауыштың бірінші және екінші жолдары бірдей болсын:
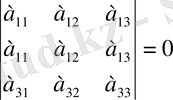
Теңдіктің дұрыстығын осы екі жолдың орындарын алмастырып 3-қасиетті қолданып тексеруге болады.
5-қасиет. Анықтауыштың бір жолын қандай да бір санға көбейтіп басқа жолға қосқаннан анықтауыш мәні өзгермейді. Үшінші ретті анықтауыштыңбірінші жолын λ-ға көбейтіп екінші жолға қосайық:
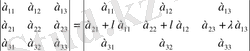
6-қасиет. Үшбұрышты матрицаның анықтауышы диагональ бойындағы элементтердің көбейтіндісінен тең:
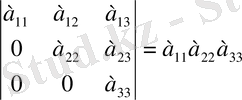
Теңдіктің дұрыстығын анықтауышты бірінші тік немесе үшінші жатық жол бойынша жіктеп тексеруге болады.
Осы қасиеттер көмегімен жоғары ретті анықтауыштар есептеуді көп жеңілдетуге болады. Анықтауышты қандай да бір жолында неғұрлым көп ноль болатындай етіп түрлендіріп, сол жол бойынша жіктеп анықтауыш реті төмендетіледі.
Кері матрица
А=(а ij ) (i, j=1, 2, …, n) квадрат матрицасын қарастырайық.
Анықтама. Анықтауышы нолге тең матрица ерекше, ал нолге тең емес матрица ерешк емес матрица деп аталады.
Кез келген
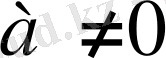 сан үшін мына
сан үшін мына
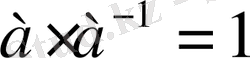 теңдігін қанағаттандыратындай кері сан табылады. Квадрат матрица үшін де осындай ұғым енгіземіз.
теңдігін қанағаттандыратындай кері сан табылады. Квадрат матрица үшін де осындай ұғым енгіземіз.
Анықтама. А квадрат матрица үшін мына
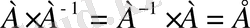
Теңдікті қанағаттандыратын А -1 матрица А матрицаның кері матрицасы деп аталады.
Кері матрицаны мына формуламен табады:

Мұндағы
 -матрица анықтауышы, ал
А
ij
-
берілген матрицаның
а
ij
элементтерінің алгебралық толықтауыштары,
i=1, 2, …, n; j=1, 2, …, n.
-матрица анықтауышы, ал
А
ij
-
берілген матрицаның
а
ij
элементтерінің алгебралық толықтауыштары,
i=1, 2, …, n; j=1, 2, …, n.
Кез келген квадрат марицаның кері матрицасы бола бермейді.
Теорема. (Кері матрица болуының қажетті және жеткілікті шарты) .
Матрицаның кері матрицасы болуы үшін ол ерекше емес
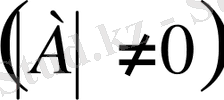 матрица болуы қажетті және жеткілікті.
матрица болуы қажетті және жеткілікті.
Мысал.
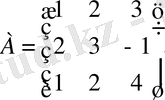 матрицасының кері матрицасын табу керек.
матрицасының кері матрицасын табу керек.
Шешуі. Алдымен анықтауышты есептейік.
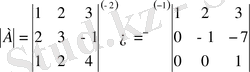
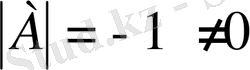 ,
Яғни кері матрица бар. Енді элементтердің алгебралық толықтауыштарын есептейік.
,
Яғни кері матрица бар. Енді элементтердің алгебралық толықтауыштарын есептейік.
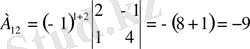
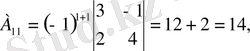
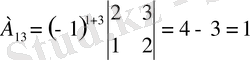 ,
,
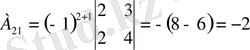
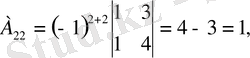
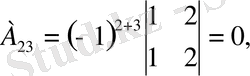
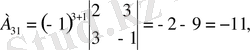
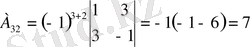
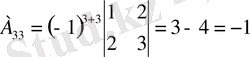
Табылған матрицаны формулаға қойып кері матрицаны табамыз.
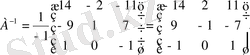
Кері матрицаның дұрыс табылғандығын
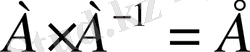 теңдігін тексеру арқылы көз жеткізуге болады. Егер
теңдігін тексеру арқылы көз жеткізуге болады. Егер
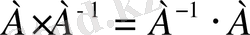 тепе-теңдігі орындалмаса, онда кері матрицаны есептеп табу барысында қате кеткені. Сондықтан да кері матрица элементтерін іздестіргенде, өте мұқият болу керек.
тепе-теңдігі орындалмаса, онда кері матрицаны есептеп табу барысында қате кеткені. Сондықтан да кері матрица элементтерін іздестіргенде, өте мұқият болу керек.
Матрица рангісі
Mxn өлшемді а матрицаның бірнеше жатық және тік жолдарын сызып тастап
k
өлшемді,
k≤
min
(m, n)
квадрат матрица алуға болады. Осы квадрат матрица анықтауышы берілген матрицаның
k
өлшемді миноры
деп аталады. А
mxn
матрицасының
k
өлшемді минорлар саны
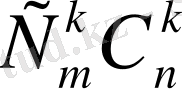 болады.
болады.
Анықтама. Матрицаның нөлге тең емес минорларының ең үлкен реті Матрица рангісі деп аталады:
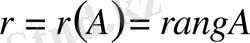
Анықтамадан бірден мынадай тұжырым жасауға болады:
1. А mxn матрицасының рангісі оның өлшемдерінің кішісінен артпайды:
r(A) ≤min(m, n) .
2. Барлық элементтері ноль болғанда ғана (нольдік матрица) матрица рангісіне тең болады.
3. n-ретті квадрат матрица ерекше емес болғанда матрица рангісі n-ге тең болады.
Мысал.
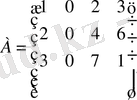 матрицасының рангісін есептейік.
матрицасының рангісін есептейік.
Шешуі. Матрица өлшемі 3x4 болғандықтан, оның рангісін 3-тен артпайды, r(A) ≤min(3, 4) . Егер үшінші ретті минорлардың ең болмағанда біреуі нолден өзгеше болса, онда матрица рангісі 3-ке тең болады. Үшінші ретті минорлар матрицаның бір тік жолын сызып тастағанда пайда болады:
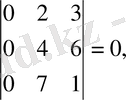
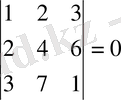
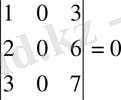
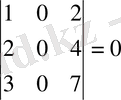
Үшінші ретті минорлардың бәрі нөлге тең болғандықтан, ранг 3-ке тең бола алмайды. Енді екінші ретті минорлардың ішінен ең болмағанда бір нөлге тең емес минор тапсақ, матрица рангісі 2-ге тең болады. Екінші ретті минорлар матрицаның бір жатық, екі тік жолын сызып тастағанда пайда болады. Айталық бірінші жатық жол мен бірінші және екінші тік жолдарды сызып тастағанда пайда болатын мына минор:
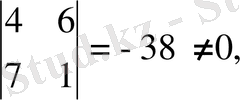 сондықтан r(А) =2
сондықтан r(А) =2
Матрица өлшемі артқан сайын оның рангісін барлық нолден өзге минорларды есептеу жолымен анықтау қиындайды. Матрица рангісін элементар түрлендірулер әдісімен табу ондай қиындықтардан тұрады.
Теорема. Элементар түрлендірулер матрица рангісін өзгертпейді.
Дәлелдеуі. Матрицаға элементар түрлендірулер жүргізгенде оның анықтауышы не өзгермей сақталады, не нолге тең емес санға көбейтіледі. Яғни, оның реті өзгермейді деген сөз. Олай болса, нолден өзгеше минорлардың немесе матрица рангісінің реті де өзгермейді.
Осы теореманы ескеріп, элементар түрлендірулер жасап, берілген матрицаны барлық диагональдық элементтері нолден өзгеше болатындай етіп сатылы түрге келтіреміз:
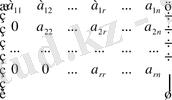 ,
,
Мұндағы r≤n. Осы шарттың орындалуын матрицаны транпонерлеу арқылы қамтамасыз етуге болады.
Сонда матрицаның r-ретті нолден өзге миноры

Бар болады да, матрица рангісі r-ге тең болады, яғни
r(A) =r.
Меншік мәндер және меншік векторлар
.
Анықтама.
А сызықтық операторының x≠0 векторы меншік вектор деп аталады, егер
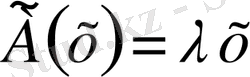 сияқты
сияқты
 саны бар болса.
саны бар болса.
 саны х векторына сәйкес келетін
саны х векторына сәйкес келетін
 операторының меншік мәні деп аталады.
операторының меншік мәні деп аталады.
Анықтама бойынша менік вектор
 операторының әсерінен өзіне өзі коллинеар векторға көшеді немесе кейбір санға көбейтіледі. Сонымен қатар меншік векторлар күрделі жолмен құрылады. Сол себепті меншік ветор мәні және мағынасы матеметикалық алгебранының көптеген сұрақтарын талдағанда өте ыңғайлы және қажетті болып табылады.
операторының әсерінен өзіне өзі коллинеар векторға көшеді немесе кейбір санға көбейтіледі. Сонымен қатар меншік векторлар күрделі жолмен құрылады. Сол себепті меншік ветор мәні және мағынасы матеметикалық алгебранының көптеген сұрақтарын талдағанда өте ыңғайлы және қажетті болып табылады.
Мына тепе-теңдікті матрица түріне келтіруге болады:

 Немесе
Немесе
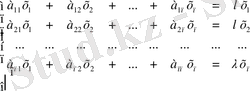
Жүйенің оң жағына нолді шығарып жазамыз:
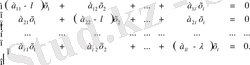
Бұл жүйенің шешімі әрдаым ноль болады х=0 =(0, 0, . . . , 0) . Жүйені анықтау үшін нолдік шешімнің болуы қажетті және жеткілікті.

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz