Аддитивті және мультипликативті модельдер

Пән: Автоматтандыру, Техника
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 11 бет
Таңдаулыға:

Аддитивті және мультипликативті модельдер.

Маусымды және циклді ауытқулары бар уақыттық қатардың құрылымын талдаудың бірнеше әдістері бар. Ең қарапайымы - орташа тегістеу әдісі. Орташа тегістеу әдісі көмегімен, маусым компонентасын есептеп, уақыттық қатардың аддитивті және мультипликативті моделін құру. Аддитивті модельдің жалпы көрінісі:

Y = S + T + E

яғни, уақыттық қатардың әр деңгейін Т- тренд, S - маусым және Е - кездейсоқ компоненттер қосындысы ретінде жазуға болады.

Мультипликативті модельдің жалпы көрінісі:

Y = S * T * E

яғни, уақыттық қатардың әр деңгейін Т - тренд, S - маусым және Е - кездейсоқ компоненттер көбейтіндісі ретінде жазуға болады.

Осы екі модельдің бірін таңдап алу, маусымдық ауытқуын талдауға негізделген. Егер ауытқу амплитудасы шамамен тұрақты болса, онда маусым компонентаның мәнін тұрақты деп есептеп, уақыттық қатардың аддитивті моделін құрамыз. Егер ауытқу амплитудасы өссе немесе кемісе, онда уақыттық қатардың маусым компонента мәніне тәуелді болатын мультипликативті модельін құрамыз.

Аддитивті және мультипликативті модельді құру, уақыттық қатардың әр деңгейі үшін маусымдық, тренд, кездейсоқ компоненталарын есептеуге негізделген . Ол келесі қадамдардан тұрады:

1) Берілген уақыттық қатарда өзгермелі орташа әдісі көмегімен тегістеу.

2) S маусым компонентасының мәнін анықтау.

3) Берілген уақыттық қатар деңгейінен маусым қатарын шығырып, аддитивті модельде T + E, ал мультипликативті модельде T * E тегістелген мәндерін есептейміз.

4) T + E немесе T * E деңгейлерін аналитикалық тегістеу және алынған тренд теңдеуі көмегімен, T мәндерін есептеу.

5) Алынған модель көмегімен T + S аддитивті модельде немесе T * S мультипликативті модельде мәндерін есептеу.

6) Абсалютті немесе салыстырмалы қателерді есептеу. Егер алынған қате мәндерінде автокорреляция жоқ болса, онда алғашқы қатар мен басқа уақыттық қатар арасындағы өзара байланысты талдау үшін, E қате уақыттық қатарын қарастырамыз.

Енді әрбір модельдің толық құрылымын келесі мысалдардан көреміз.

Маусымдық қатардың аддитивті модельдің құрылуы.

Мысал. Қ. Р 1994-1998 ж. ж өндірістік өнеркәсіптік бизнес циклі.

( Кесте 1) .

1 Қадам.

Берілген уақыттық қатарды, өзгермелі орташа әдісі көмегімен тегістейміз. Ол үшін:

а) әрбір 4 квартал бойынша тізбектелетін қатар деңгейлерінің мәндерін қосып, оны бір уақыт мезетіне жылжытып орналастырамыз.

б) алған соманы төртке бөліп, өзгермелі орташа мәнін табамыз. Осы жолмен алынған тегістелген мәндерінде маусымдық компонента болмайды.

в) бұл мәндерді сәйкесінше нақты уақыт мезетіне әкелеміз, ол үшін, екі тізбектелген өзгермелі орташаның орта мәнін табамыз, яғни - орталықтандырылған өзгермелі орташа.

Кесте 1.

Квартал №: Квартал №

Шығарыл-ымы млрд. тең.: Шығарыл-ымы млрд. тең.

4 кв. б-ша қорытынды: 4 кв. б-ша қорытынды

4 кв. өзгермелі орташасы.: 4 кв. өзгермелі орташасы.

Орталықтандырылған өзгермелі орташа: Орталықтандырылған өзгермелі орташа

Маусым комп.Бағасы. S^:

Маусым комп.

Бағасы. S^

Квартал №: 1

Шығарыл-ымы млрд. тең.: 91, 92

4 кв. б-ша қорытынды:

4 кв. өзгермелі орташасы.:

Орталықтандырылған өзгермелі орташа:

Маусым комп.Бағасы. S^:

Квартал №: 2

Шығарыл-ымы млрд. тең.: 88, 74

4 кв. б-ша қорытынды:

4 кв. өзгермелі орташасы.:

Орталықтандырылған өзгермелі орташа:

Маусым комп.Бағасы. S^:

Квартал №: 3

Шығарыл-ымы млрд. тең.: 82, 81

4 кв. б-ша қорытынды: 354, 11

4 кв. өзгермелі орташасы.: 88, 5275

Орталықтандырылған өзгермелі орташа: 87, 7725

Маусым комп.Бағасы. S^: -4, 9625

Квартал №: 4

Шығарыл-ымы млрд. тең.: 90, 64

4 кв. б-ша қорытынды: 348, 07

4 кв. өзгермелі орташасы.: 87, 0175

Орталықтандырылған өзгермелі орташа: 85, 73375

Маусым комп.Бағасы. S^: 4, 90625

Квартал №: 5

Шығарыл-ымы млрд. тең.: 85, 88

4 кв. б-ша қорытынды: 337, 8

4 кв. өзгермелі орташасы.: 84, 45

Орталықтандырылған өзгермелі орташа: 83, 45375

Маусым комп.Бағасы. S^: 2, 42625

Квартал №: 6

Шығарыл-ымы млрд. тең.: 78, 47

4 кв. б-ша қорытынды: 329, 83

4 кв. өзгермелі орташасы.: 82, 4575

Орталықтандырылған өзгермелі орташа: 81, 68625

Маусым комп.Бағасы. S^: -3, 21625

Квартал №: 7

Шығарыл-ымы млрд. тең.: 74, 84

4 кв. б-ша қорытынды: 323, 66

4 кв. өзгермелі орташасы.: 80, 915

Орталықтандырылған өзгермелі орташа: 81, 07125

Маусым комп.Бағасы. S^: -6, 23125

Квартал №: 8

Шығарыл-ымы млрд. тең.: 84, 47

4 кв. б-ша қорытынды: 324, 91

4 кв. өзгермелі орташасы.: 81, 2275

Орталықтандырылған өзгермелі орташа: 81, 33625

Маусым комп.Бағасы. S^: 3, 13375

Квартал №: 9

Шығарыл-ымы млрд. тең.: 87, 13

4 кв. б-ша қорытынды: 325, 78

4 кв. өзгермелі орташасы.: 81, 445

Орталықтандырылған өзгермелі орташа: 81, 185

Маусым комп.Бағасы. S^: 5, 945

Квартал №: 10

Шығарыл-ымы млрд. тең.: 79, 34

4 кв. б-ша қорытынды: 323, 7

4 кв. өзгермелі орташасы.: 80, 925

Орталықтандырылған өзгермелі орташа: 81, 04

Маусым комп.Бағасы. S^: -1, 7

Квартал №: 11

Шығарыл-ымы млрд. тең.: 72, 76

4 кв. б-ша қорытынды: 324, 62

4 кв. өзгермелі орташасы.: 81, 155

Орталықтандырылған өзгермелі орташа: 80, 82875

Маусым комп.Бағасы. S^: -8, 06875

Квартал №: 12

Шығарыл-ымы млрд. тең.: 85, 39

4 кв. б-ша қорытынды: 322, 01

4 кв. өзгермелі орташасы.: 80, 5025

Орталықтандырылған өзгермелі орташа: 80, 84375

Маусым комп.Бағасы. S^: 4, 54625

Квартал №: 13

Шығарыл-ымы млрд. тең.: 84, 52

4 кв. б-ша қорытынды: 324, 74

4 кв. өзгермелі орташасы.: 81, 185

Орталықтандырылған өзгермелі орташа: 82, 68375

Маусым комп.Бағасы. S^: 1, 83625

Квартал №: 14

Шығарыл-ымы млрд. тең.: 82, 07

4 кв. б-ша қорытынды: 336, 73

4 кв. өзгермелі орташасы.: 84, 1825

Орталықтандырылған өзгермелі орташа: 84, 3425

Маусым комп.Бағасы. S^: -2, 2725

Квартал №: 15

Шығарыл-ымы млрд. тең.: 84, 75

4 кв. б-ша қорытынды: 338, 01

4 кв. өзгермелі орташасы.: 84, 5025

Орталықтандырылған өзгермелі орташа: 84, 32875

Маусым комп.Бағасы. S^: 0, 42125

Квартал №: 16

Шығарыл-ымы млрд. тең.: 86, 67

4 кв. б-ша қорытынды: 336, 62

4 кв. өзгермелі орташасы.: 84, 155

Орталықтандырылған өзгермелі орташа: 83, 934125

Маусым комп.Бағасы. S^: 2, 735875

Квартал №: 17

Шығарыл-ымы млрд. тең.: 83, 13

4 кв. б-ша қорытынды: 334, 853

4 кв. өзгермелі орташасы.: 83, 71325

Орталықтандырылған өзгермелі орташа: 83, 25825

Маусым комп.Бағасы. S^: -0, 12825

Квартал №: 18

Шығарыл-ымы млрд. тең.: 80, 303

4 кв. б-ша қорытынды: 331, 213

4 кв. өзгермелі орташасы.: 82, 80325

Орталықтандырылған өзгермелі орташа: 81, 95575

Маусым комп.Бағасы. S^: -1, 65275

Квартал №: 19

Шығарыл-ымы млрд. тең.: 81, 11

4 кв. б-ша қорытынды: 324, 433

4 кв. өзгермелі орташасы.: 81, 10825

Орталықтандырылған өзгермелі орташа:

Маусым комп.Бағасы. S^:

Квартал №: 20

Шығарыл-ымы млрд. тең.: 79, 89

4 кв. б-ша қорытынды:

4 кв. өзгермелі орташасы.:

Орталықтандырылған өзгермелі орташа:

Маусым комп.Бағасы. S^:

2 Қадам.

Маусым компонентаның бағасын, берілген қатар деңгейлерімен орталықтандырылған өзгермелі орташа арасындағы айырым деп анықтап, оны S - маусым компонентасының мәнін есептеуде пайдаланамыз.

Аддитивті модельде маусымдық компонентінің есептелуі.

Кесте 2.

Көрсеткіштер: Көрсеткіштер

Жыл: Жыл

i, кварталының №: i, кварталының №

Көрсеткіштер: 1

Жыл: 2

i, кварталының №: 3

Көрсеткіштер:

Жыл: 1

i, кварталының №:

-4, 9625

4, 90625

Көрсеткіштер:

Жыл: 2

i, кварталының №: 2, 42625

-3, 21625

-6, 23125

3, 13375

Көрсеткіштер:

Жыл: 3

i, кварталының №: 5, 945

-1, 7

-8, 06875

4, 54625

Көрсеткіштер:

Жыл: 4

i, кварталының №: 1, 83625

-2, 2725

0, 42125

2, 735875

Көрсеткіштер:

Жыл: 5

i, кварталының №: -0, 12825

-1, 65275

Көрсеткіштер: i-шы квартал жиыны

Жыл:

i, кварталының №: 10, 07925

-8, 8415

-18, 8413

15, 32213

Көрсеткіштер: маусм. ком. орт. бағ. S^

Жыл:

i, кварталының №: 2, 519813

-2, 21038

-4, 71031

3, 830531

Көрсеткіштер: S^ маусм. комп. тегіс.

Жыл:

i, кварталының №: 2, 662398

-2, 06779

-4, 56773

3, 973117

Маусымдық компонентасы бар модельдерде әр кезеңде маусымдық әсерлер өзара жойылады деп есептеледі. Аддитивті модельде барлық квартал бойынша маусым компонентасы мәндерінің сомасы нөлге тең болу керек.

Берілген модель үшін:

2, 519813 - 2, 21038 - 4, 71031 + 3, 830531 = - 0, 570

Түзету коэфицентін анықтаймыз:

k = - 0, 570346/4 = - 0, 1425865

Маусымдық компонентаның түзету мәнін, орташа бағасымен k түзету коэфицентінің арасындағы айырым ретінде қарастырамыз:

Si = Si орт - k

Маусымдық компонента сандарының қосындысы нольге тең болатын шартын тексереміз:

2, 662398 - 2, 06779 - 4, 56773 + 3, 973117 = 0

3 Қадам.

Берілген уақыттық қатар деңгейінен маусым қатарын шығарамыз. T + E = Y - S (Кесте 3) . Бұл мәндер әрбір уақыт кезеңіне есептеледі.

Аддитивті модельдің E қатесімен Т тегістелген белгісін анықтау.

Кесте 3.

t: t

Yt: Yt

S: S

T+E=Yt-Si: T+E=Yt-Si

T: T

T+S: T+S

E=Yt-(T+S): E=Yt-(T+S)

E^2: E^2

t: 1

Yt: 91, 92

S: 2, 662398

T+E=Yt-Si: 89, 257602

T: 86, 073

T+S: 88, 7354

E=Yt-(T+S): 3, 184602

E^2: 10, 14169

t: 2

Yt: 88, 74

S: -2, 06779

T+E=Yt-Si: 90, 807789

T: 85, 775

T+S: 83, 70721

E=Yt-(T+S): 5, 032789

E^2: 25, 32897

t: 3

Yt: 82, 81

S: -4, 56773

T+E=Yt-Si: 87, 37773

T: 85, 477

T+S: 80, 90927

E=Yt-(T+S): 1, 90073

E^2: 3, 612775

t: 4

Yt: 90, 64

S: 3, 973117

T+E=Yt-Si: 86, 666883

T: 85, 179

T+S: 89, 15212

E=Yt-(T+S): 1, 487883

E^2: 2, 213796

t: 5

Yt: 85, 88

S: 2, 662398

T+E=Yt-Si: 83, 217602

T: 84, 881

T+S: 87, 5434

E=Yt-(T+S): -1, 663398

E^2: 2, 766893

t: 6

Yt: 78, 47

S: -2, 06779

T+E=Yt-Si: 80, 537789

T: 84, 583

T+S: 82, 51521

E=Yt-(T+S): -4, 045211

E^2: 16, 36373

t: 7

Yt: 74, 84

S: -4, 56773

T+E=Yt-Si: 79, 40773

T: 84, 285

T+S: 79, 71727

E=Yt-(T+S): -4, 87727

E^2: 23, 78776

t: 8

Yt: 84, 47

S: 3, 973117

T+E=Yt-Si: 80, 496883

T: 83, 987

T+S: 87, 96012

E=Yt-(T+S): -3, 490117

E^2: 12, 18092

t: 9

Yt: 87, 13

S: 2, 662398

T+E=Yt-Si: 84, 467602

T: 83, 689

T+S: 86, 3514

E=Yt-(T+S): 0, 778602

E^2: 0, 606221

t: 10

Yt: 79, 34

S: -2, 06779

T+E=Yt-Si: 81, 407789

T: 83, 391

T+S: 81, 32321

E=Yt-(T+S): -1, 983211

E^2: 3, 933126

t: 11

Yt: 72, 76

S: -4, 56773

T+E=Yt-Si: 77, 32773

T: 83, 093

T+S: 78, 52527

E=Yt-(T+S): -5, 76527

E^2: 33, 23834

t: 12

Yt: 85, 39

S: 3, 973117

T+E=Yt-Si: 81, 416883

T: 82, 795

T+S: 86, 76812

E=Yt-(T+S): -1, 378117

E^2: 1, 899206

t: 13

Yt: 84, 52

S: 2, 662398

T+E=Yt-Si: 81, 857602

T: 82, 497

T+S: 85, 1594

E=Yt-(T+S): -0, 639398

E^2: 0, 40883

t: 14

Yt: 82, 07

S: -2, 06779

T+E=Yt-Si: 84, 137789

T: 82, 199

T+S: 80, 13121

E=Yt-(T+S): 1, 938789

E^2: 3, 758903

t: 15

Yt: 84, 75

S: -4, 56773

T+E=Yt-Si: 89, 31773

T: 81, 901

T+S: 77, 33327

E=Yt-(T+S): 7, 41673

E^2: 55, 00788

t: 16

Yt: 86, 67

S: 3, 973117

T+E=Yt-Si: 82, 696883

T: 81, 603

T+S: 85, 57612

E=Yt-(T+S): 1, 093883

E^2: 1, 19658

t: 17

Yt: 83, 13

S: 2, 662398

T+E=Yt-Si: 80, 467602

T: 81, 305

T+S: 83, 9674

E=Yt-(T+S): -0, 837398

E^2: 0, 701235

t: 18

Yt: 80, 303

S: -2, 06779

T+E=Yt-Si: 82, 370789

T: 81, 007

T+S: 78, 93921

E=Yt-(T+S): 1, 363789

E^2: 1, 85992

t: 19

Yt: 81, 11

S: -4, 56773

T+E=Yt-Si: 85, 67773

T: 80, 709

T+S: 76, 14127

E=Yt-(T+S): 4, 96873

E^2: 24, 68828

t: 20

Yt: 79, 89

S: 3, 973117

T+E=Yt-Si: 75, 916883

T: 80, 411

T+S: 84, 38412

E=Yt-(T+S): -4, 494117

E^2: 20, 19709

4 Қадам.

Берілген модельдің Т компонентасын анықтаймыз. Ол үшін сызықты тренд теңдеуін аламыз:

T = 86, 39 - 0, 2998* t

Осы теңдеуге t = 1, ………, 20 белгілерін қойып, әр уақыт үшін T табамыз . (Кесте 3)

Тренд теңдеуінің графигі 1 суретте көрсетілген.

Сурет1

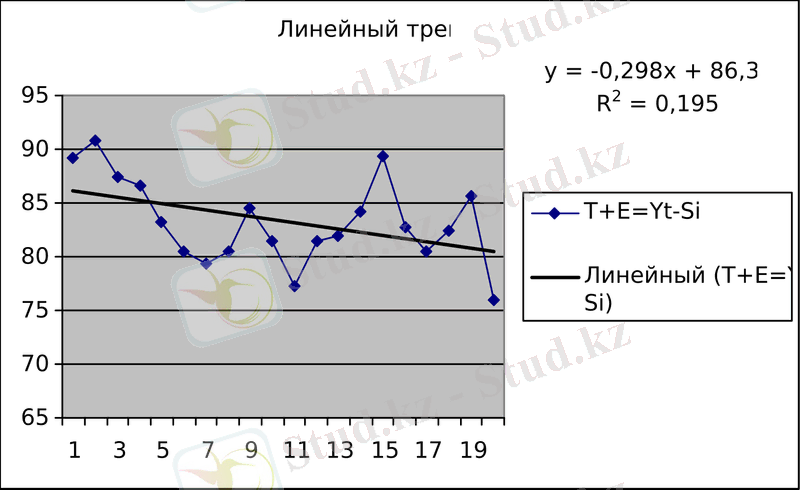
5 Қадам.

Аддитивті модельмен алынған қатар деңгейінің мәндерін анықтаймыз. Ол үшін T деңгейіне сәйкес S маусым компонентасын қосамыз. (T+S), ол 3 - кестеде көрсетілген.

6 Қадам.

Аддитивті модельдің құрылуына сәйкес қатені есептеу мына формуламен жүзеге асады:

E = Y - (T+S) .

Модельдің мәнділігін, сапасын анықтау үшін, детерминация коэфицентімен аппроксимация орташа қатесін анықтаймыз.

R^2 = 1 - ( 243, 8921 / 302, 9665 ) =0, 195

A = 1 / 20 * 0, 701352 * 100 % = 3, 506759

Енді болашақтағы екі жылға болжам жасайық. Ол үшін мына формуланы пайдаланамыз:

Y21 = T21 + S1

Y22 = T22 + S2

S1, S2 -маусымдық компонента кестеде берілген, яғни S1 = 2, 662398, ал, S2= - 2, 06779, ал T21, T22 тренд теңдеуіне қойып шығарамыз:

T = 86, 371 - 0, 298 * t

Сонда:

Y21 = 80, 113 + 2, 662398 = 82, 7754

Y22 = 79, 815 - 2, 06779 = 77, 74721

Сонымен болашақтағы екі жылға ҚР өндірістік өнеркәсіптік бизнес циклі:

82, 7754 + 77, 74721 = 160, 5226

құрайды.

Маусымдық қатардың мультипликативті моделін құру.

1 Қадам.

Берілген уақыттық қатарды өзгермелі орташа әдісі көмегімен тегістеу жургіземіз. Ол толығымен аддитивті модельмен сәйкес. Уақыттық компонентаның есептеу нәтижелері 4 кестеде көрсетілген.

4 Кесте.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.