Алгоритмдерді талдау

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 44 бет
Таңдаулыға:

Лекция № Алгоритмдерді талдау .

Тиімді, жылдам жұмыс істейтін алгоритмдер құрудың практикалық есептер шығаруда бірінші дәрежелі болмаса да, үлкен мәні бар. Бірнеше алгоритмдердің ішінен жылдам жұмыс істейтін алгоритмді таңдау үшін олардың жұмыс уақытын салыстырып үйрену қажет. Дегенмен, жұмыс уақытын дәл есептеу мүмкін емес. Бұл уақыт алдымен программа орындалатын компьютердің шынайы сипаттамасына тәуелді болуы мүмкін. Әдетте алгоритмнің орындалуы уақыты тек жуықтап қана есептеледі. Сонымен бірге жұмыс уақытына арналған формула мәндері тек тәжірибелік жолмен анықталатын қандай да бір сандық тұрақтылардан тұрады. Мұндай бағалаудың өзі көбінесе ең тиімді бір алгоритмді ғана таңдауға мүмкіндік береді. Басқа жағдайларда жұмыс уақытын бағалаудың көмегімен баяу жұмыс істейтін алгоритмдерді шығарып тастауға болады, ал қалғандарынан программаның шынайы жұмыс уақытын өлшеудің көмегімен таңдауға болады.

Енді жоғарыда айтылғандарды мысалмен түсіндірейік. Мысалы, қандай да бір n саннан құрылған тізбекті өңдеу қажет болсын. Мұндағы n өзгеріп отыратын болсын. Осы есепті шығаруға екі программа берілсін, олардың жұмыс уақыты жуықтап С ₁ n C ₂ n ² , мұндағы С ₁ және С _{2 -} - тұрақтылар, олар n-ге тәуелсіз. N үлкен болған жағдайда бірінші программа жылдам жұмыс істейді, ал n аз шама болғанда программа баяу жұмыс істейді. Бұл С ₁ > С ₂ екенін көрсетеді. С ₁ С ₂ -ден 5 есе үлкен болсын. С ₁ =5С ₂ . С ₁ n =5С ₂ n мен C ₂ n ² -ты салыстыра отырып, n>5 болғандағы программаның жұмыс уақытының баяу, ал n<5 болғанда екінші программаның жылдам жұмыс істейтінін байқауға болады. Мұндағы n =5 бағалау уақытының шектік мәні де жуықтап тағайындалады.

Бұдан екі тұжырым жасауға болады. Біріншіден, «тұрақтыға дейінгі дәлдікпен» жуықтап бағалаудың өзі алгоритмдерді салыстыруда пайдалы болып табылады. Екініден, есеп шығарудың бір алгоритмі өте жылдам деп айтуға болмайды. Қандай да бір алғашқы мәліметтер жиынтығы үшін кейбір алгоритм екіншісінен тиімді болуы мүмкін.

Енді программаның жұмыс уақытын анықтайтын алғашқы мәліметтердің мұндай сипаттамасын таңдау мәселесіне тоқталайық. Мұндай сипаттама есептің өлшемі деп аталады. Әртүрлі есептерді шығару уақытына алғашқы мәліметтердің әртүрлі қасиеті әсер етеді. Мысалы, минимумды іздеу немесе әрбір сан бір бүтін сан ретінде қарастырылатын берілген сандарды іріктеу типті есептер үшін алғашқы сандар мөлшері есептер мөлшері болып табылады. Қарапайым көбейткіштерге жіктеу есебі үшін санның шамасы мөлшері болып есептеледі. Есеептің мөлшерін таңдау қандай да бір шығару алгоритмі туралы жалпы ұғымға негізделеді. 2 ⁿ дәрежесін есептеу алгоритмін қарастырайық. Дәрежелеудің санның бірінен соң бірі көбейтілетінін ескере отырып, өлшем ретінде n дәреже көрсеткішті аламыз. Өлшемді сипаттаудың тағы бір тәсілі нәтижедегі цифр сан ыболып табылады. 2 ⁿ дәрежесіндегі цифр саны n-ге пропорционал, сондықтан екі өлшем де эквивалентті.

Жұмыс уақытын бағалау мезетіндегі маңызды кезең - орындалу барысында барлық жұмыс уақытының негізгі бөлігін алатын программа бөлігін іздеу болып табылады. Көптеген программалар үшін экспериментті түрде дәлелденген факт: жұмыс уақытының негізгі бөлігі программа мәтінінің шағын бөлігін орындауға кетеді. Программаның мұндай бөлігі цикл деп аталады. Көпшілік жағдайда жұмыс уақытын жуықтап бағалау талап етіледі, сондықтан программаның қалған бөлігінің орындалу уақытын ескермеуге болады, тек ішкі циклдың орындалуын қарастыруға болады.

Егер программа бірінің ішіне бірі орналасқан бірнеше программадан тұратын болса, онда ішкі циклды табу жеңіл. Әрине, алдымен, бәрінен бұрын барлық циклға қатысты программа бөлігі орындалады, ал бұл қалған барлық циклдардың ішіндегі және ішінде басқа цикл болмайтын циклдар болып табылады. Бұл бақылау программаның жиі орындалатын бөлігі үшін «ішкі цикл» деген атауды дәлелдей түседі.

Егер ішкі циклды қамтымайтын бірнеше цикл болса, олардың әрқайсысының қайталану санын есептеуге болады. Егер бір циклдың қайталану саны басқаларымен салыстырғанда айтарлықтай үлкен болатын болса, онда басқа циклдардың жұмыс уақытын ескермеуге болады; кері жағдайда соңғы формулада жұмыс уақыты үшін бірнеше циклдардың орындалу уақытын ескеруге тура келеді. Параметрлі қайталану командасындағы қайталану саны For операторы үшін төмендегі формуламен есептеледі:

Циклдың басы For i:=A to B

Егер B>=A-1 болса, онда қайталану саны B - A +1 -ге тең;

Егер B<A болса, онда нөлге тең; (1)

For i:=A downto B циклі үшін А мен В-ның орындарын ауыстыру қажет.

Егер программада цикл бір рет орындалатын болса, онда бұл формула ақиқат болып есептеледі. Енді бұл циклдың басқа циклдың ішінде бірнеше рет қайталанып орындалған жағдайын қарастырайық. Цикл ішіндегі қайталану санын шартты түрде цикл денесінің орындалу санының саны деп атайық. Барлық циклдың орындалу санын цикл тақырыбының орындалу саны деп атайық. Сөйтіп, цикл тақырыбының бір рет орындалуы цикл денесінің қанша рет орындалатынын көрсетеді. Бірінші формула оның тақырыбы цикл денесінің бір рет орындалуындағы цикл денесінің орындалу санын береді. Егер қарастырылып отырған цикл басқа циклдың ішінде орналасқан болса, онда онда оның тақырыбы бірнеше рет орындалады да, цикл денесінің орындалуының жалпы санын табу үшін осы цикл тақырыбының барлық орындалуы барысындағы (1) формуламен алынған сандарды қосу қажет.

Бұл формуланы қолданудың қарапайым мысалы ретінде төмендегі программа фрагментін талдайық:

For j:=1 to n do

Begin (*1-цикл *)

For k:=1 to M do (* 2-цикл денесі*)

For l:=n downto j do (* 3-цикл денесі*)

End;

Екінші және үшінші цикл денелерінде ішкі цикл жоқ, ал, M және N - қандай да бір үлкен тұрақтылар. 2 және 3-циклдардың қайталану санын бағалайық. Екеуі де бірінші циклдың ішінде орналасқан, олардың қай талану саны (1) формула бойынша оңай есептеледі; ол N-1+1=N-ге тең. Бұл қайталанулардың әрқайсысында 2-цикл денесі М-1+1=М рет орындалады. М саны тұрақты болғандықтан 2-цикл денесінің жалпы орындалу саны N ₂ = N∙М тең. 3-цикл денесі 1-цикл денесінің әрбір орындалуында N-J+1 рет орындалады. Бұл санның М санынан айырмашылығы 1-циклдың орындалуы барысында өзгеріп отырады; сондықтан екі санды тек көбейте салуға болмайды:3-цикл денесінің барлық орындалу санын қосу қажет. Бұдан 1-циклдың орындалуында J айнымалысы 1-ден N-ге дейінгі барлық мәндерді қабылдайды (міне дәл осы 1-цикл тақырыбында жазылған. Сөйтіп, 3-цикл денесінің жалпы орындалу саны:

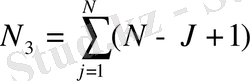
Бұл арифметикалық прогрессияны ңқосындысы; ол (N+1) ∙ N/2 тең. Уақыт жуықтап есептелінетіндіктен N-мен салыстыруға жүгібей-ақ, формуланы жеңілдетуге болады: N ₃ жуықтап N ² /2 тең. N ₂ мен N ₃ -ті салыстыра отырып, бұл сандардың біреуі екіншісінен әлдеқайда артық деп айта алмаймыз. Керісінше, қандай да бір N мен М үшін олар бір ретте болады. Мысалы, егер М= N, онда N ₂ шамамен N ₃ -тен 2 есе үлкен болады. Сондықтан жұмыс уақыты үшін формулаға екі циклға да жауап беретін екі қосылғыш қосуға тура келеді. Цикл денелерінің бір реттік орындалу уақытын есептей отырып, тұрақтыларды Т ₂ және Т ₃ арқылы белгілеп, жалпы жұмыс уақытын есептеу үшін төмендегідей жуықтатылған формуланы аламыз:

Т =М∙N∙Т ₂ +(N ² /2) ∙Т ₃ .

Егер цикл денелерінің орындалу уақытын тұрақты деп есептемейтін болса (мысалы, онда шартты оператор немесе процедураны шақыру болса), онда алдымен денелердің орындалу уақытын талдап, одан кейін оларды қосу қажет.

Жұмыс уақыты жөнінде бұдан да дәл ақпаратты әртүрлі алғашқы мәліметтер бойынша программа программа жұмысының шынайы уақытын өлшеу нәтижесі бойынша алуға болады. Бұл эксперименттердің көмегімен формулаға кіретін белгісіз тұрақтыларды (біздің жағдайда Т ₂ және Т ₃ ) бағалауға болады.

Енді нақты программа жұмысын талдауға көшейік, 2 ^N дәрежесін есептеуді қарастырайық. Программа жұмысы циклды қамтитын екі ірі бөліктен тұрады. Ол 2 ^N дәрежесін есептеу және баспаға шығару. Программаның жұмыс уақытын бағалауда әдетте, баспаға шығару уақытын емес, тек есептеуге кететін уақыт ескеріледі. Бұл көптеген есепті шығару алгоритмі үшін басу уақыты өте аз болғандықтан ескерілмейді. Сонымен қатар, өте үлкен N үшін есептеу уақыты аз болғандықтан ескермеуге де болады. Басып шығаруды және циклған кірмейтіндерді шығарып тастағаннан кейін төмендегідей программма аламыз:

For K:=1 To N Do Begin (*1-цикл*)

For I:=еңҮлкенҰзындық DownTo XБасы Do Begin

(*2-цикл *)

Құрамында циклы жоқ әрекеттер

End;

Құрамында циклы жоқ әрекеттер

End;

Бір цикл, дәлірек айтсақ, 2-циклға басқа цикл кірмейді. Ол ішкі цикл болып қалады. Енді оның денесінің қайталану санын есептейік. 2-цикл денесінің орындалу саны МАХұзындық-Хбасы+1-ге тең, жұмыс барысында ХБасы мәнінің өзгеруінің есебінен өзгереді. Мұнда ХБасы мәнінің 1-циклды басқаратын К мәніне қаншалықты тәуелді екенін біз білмейміз. 2-цикл денесінің орындалу санын N ₂ (К) арқылы белгілей отырып, төмендегідей қосындыны есептеу қажеттілігіне көз жеткіземіз:

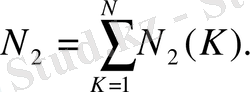
N ₂ (К) функциясын табу үшін алгоритмді мазмұны жағынан талдау қажет. (1) формуланы тікелей қолдану ыңғайсыз. Мұның орнына 2-цикл тақырыбының әрбір орындалуында оның денесінің орындалу саны екі еселенген цифрларының санына тең екенін байқаймыз. Программа мәтінінен байқалғанындай екі еселенген сан 2 ^К-1 -не тең. Кез келген натурал санның цифрларының саны оның ондық логарифмінің бір бүтін бөлігіне көбейтіндісіне тең, 2 ^К-1 -нің ондық логарифмі (К-1) *lg2-ге тең, мұндағы lg2 жуықтап 0, 3-ке тең. Сөйтіп, N ₂ (К) үшін төмендегідей формуланы аламыз:

N ₂ (К) = 1+[(K+1) Lg2] .

Мұндайжалпы мүшесі бар қосындыны есептеу қиын. Есептеуді жеңілдету үшін жуықтатылған санға көшеміз. Санның бүтін бөлігі өзінен 1-ге жуық ажырыатылатынын байқаймыз. Бұл айырмашылықты ескермей, логарифмнің бүтін бөлігіні логарфимнің өзімен алмастырамыз. Жалпы мүшесі 1+[(K+1) Lg2] болатын арифметикалық прогрессияның қосындысын табу қажет. Қосынды төмендегі формуламен есептеледі:

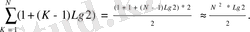
Соңғы шамаға көшу барысында N* Lg2-мен салыстырғанда шамасы кіші болатын 2- Lg2 қосылғышын ескермедік. Сондай-ақ, қорытынды нәтижені де бірден алуға болатын еді, егер і+(К-1) Lg2 шамасын К* Lg2-ге жуықтап алмастырса, ал, арифметикалық прогрессияның қосындысын табуға арналған формулада прогрессияның алғашқы мүшесін алмауға болады. Барлық бұл ауыстырулардың қателігі бір ретті және жуықтап қорытынды нәтиженің 1/N бөлігін құрайды.

Сөйтіп, 2-циклдың орындалуының қорытынды уақыты барлық программа бойынша есептеудің негізгі бөлігін құрайды, ол:

N ² ∙ Lg2/2∙Т ₂ ≈0, 15∙N ² ∙Т ₂ тең.

Мұндағы Т ₂ -цикл денесінің бір рет орындалу уақыты.

Сөйтіп, біз 2 ^N дәрежесін есептеу программасының жұмыс уақытын бағалауды жүргіздік. Жұмыс уақытын бағалау барлық уақытта қажет және оны программаны құру кезінде орындау қажет.

Енді WHILE-DO типті қайталану алгоритмінің жұмыс уақытын талдау мысалын қарастырайық. Бүтін санды натурал санға дәрежелеу функциясының жұмыс уақытын талдайық. Мұны есептеу функциясының мәтінеі төмендегідей:

Function Dareje (M, N:integer) :integer;

{М - дәреженің негізі, N - дәреже көрсеткіш}

Var M1, N1, P:integer; {Р -нәтижені есептейтін айнымалы}

Begin

P:=1; M1:=M; N1:=N;

WHILE N1<>0 do {сыртқы цикл}

Begin

WHILE N1 mod 2 =0 do

Begin {ішкі цикл}

N1:=N1 div 2; M1:=M1*M1;

{N1 дәрежелі М1-дің мәні өзгерген жоқ}

End; {ішкі циклдың соңы}{}

N1:=N1-1; P:=P*M1 {Нәтижеге N дәрежелі М меншіктеледі}

End; {Сыртқы циклдың соңы}

Dareje:=P;

END;

Есептің өлшемі қызметін N дәреже көрсеткішінің мәні атқарады. Уақыттың негізгі бөлігі циклды орындауға кетеді. Дегенмен, ішкі циклды орындауға кететін уақыт сыртқы циклды орындауға кететін уақыттан айтарлықтай көп деген тұжырым жасауға болмайды, өйткені тақ N1 үшін ішкі цикл денес іорындалмайды. Сыртқы цикл денесінің бір рет орындалу уақытын Т _1, сыртқы цикл денесінің орындалу санын К ₁ арқылы белгілейік. Ал, Т ₂ және К ₂ - сәйкес ішкі циклдың сипаттамалары. Функцияның жалпы жұмыс уақыты Т(N) жуықтап Т(N) = Т ₁ ∙ К ₁ + Т ₂ ∙ К ₂ тең. К ₁ мен К ₂ -ні бағалау үшін N ₁ -дің кему процесін қадағалайық. Dareje функциясы N ₁ -дің жұптығын, 2-ге бөлінетіндігін тексеру операциясын қамтиды. Бұл алгоритмді талдау үшін N ₁ -дің мәнінің екілік санау жүйесіндегі жазылуын қарастыру қажет деген ойға жетелейді. (А санының негізі b болатын позициялық санау жүйесіндегі а _m a _m-1 …a ₁ a ₀ цифрларымен жазылуы:

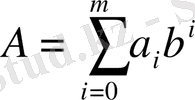-ге тең.

B=2 болғанда 0 және 1 цифрлары арқылы жазылған санның екілі жүйедегі жазылуын аламыз. Мысалы, екілік жүйедегі 1001 саны ондық жүйедегі 9 санының жазылуы. К ₁ және К ₂ -ні табу үшін N1 мәніндегі бір ең кіші екілік цифрды өңдеу барысында ішкі және сыртқы циклдардың қанша рет орындалатынын есептеу қажет. Мұнда үш түрлі жағдай қарастырылуы мүмкін.

1. N1=1. Ішкі цикл орындалмайды; ал сыртқы цикл бір рет орындалады; N1 0-ге дейін кеміп, циклдан шығады.

2. N1>1, N1 нөлмен аяқталады (яғни жұп) . Ішкі цикл бір рет орындалғаннан кейін N1 2-ге бөлінеді. Екілік жүйеде екіге бөлу ең кіші цифрды шығарып тастағанмен бірдей. Сөйтіп, ең кіші нөлді өңдеу үшін ішкі циклдың бір рет орындалуы жеткілікті.

3. N1≤1, N1 бірмен аяқталады (тақ) . Ішкі цикл орындалмайды, сыртқы циклда N1-ден 1-алып тастайды, яғни N1 жұп болып қалады. Сөйтіп, 2-жағдайға келеміз. Ең кіші бірлікті өңдеу үшін ішкі және сыртқы циклдың бір реттен орындалуы талап етіледі.

Бірінен соң бірі өңделіп, N1 цифрының барлық екілік цифрлары шығарылып тасталынады. Сонымен, бастапқы N1= N жағдайды ескере отырып,

К ₁ = N-нің екілік жазылуындағы берліктер саны,

К ₂ = (N-нің екілік жазылуындағы цифрлар саны) -1

екенін аламыз.

N-нің екілік жазылуындағы цифрлар саны N-нің екілік логарифмінің бүтін бөлігін 1-ге арттырғанмен бірдей, яғни

К ₂ = [log ₂ N] .

К ₂ үшін мұндай қарапайым формуланы жаза алмаймыз, сондықтан К ₁ -ді жоғарыдан ғана бағалай аламыз. Бірліктер саны цифрлар санынан көп болмайтыны белгілі,

К ₁ ≤1+[log ₂ N] .

Бұдан

Т(N) ≤ (1+[log ₂ N] ) ∙ Т ₁ + [log ₂ N] ∙Т ₂ =( Т ₁ + Т ₂ ) ∙ [log ₂ N] + Т ₁ .

Теңдік N екілік жүйеде тек 1-лермен жазылған жағдайда ғана теңдік орындалады, яғни екінің дәрежесі 1-ге кем. N екілік жүйедегі жазылуында бірліктер қаншалықты аз болса, онда Dareje функциясы соншалықты жылдам жұмыс істейді. Егер N екінің дәрежесі болса, К ₁ минимумға жетеді, ал жалпы уақыт

Т(N) = Т ₁ + log ₂ N ∙Т _{2 .}

Енді Dareje функциясын tyzusyzykty функциясымен салыстырып көрейік.

Function tyzusyzykty (M, N:integer) :integer;

{М - дәреженің негізі, N - дәреже көрсеткіш}

Var M1, N1, P:integer; {Р -нәтижені есептейтін айнымалы}

Begin

P:=1; M1:=M; N1:=N;

WHILE N1<>0 do

Begin

N1:=N1-1; P:=P* M1;

End;

Tyzusyzykty:=P;

END;

Бұл функцияның жұмыс уақытын ТС(N), ал циклдың бір рет орындалуын ТС ₁ арқылы белгілейік.

ТС(N) ≈ N · ТС ₁ болсын. N -мен салыстырғанда log ₂ N баяу өсетіндіктен, N-нің шамасы өте үлкен болған жағдайларда Т(N) < ТС(N) болады, N-нің шамасы артқан сайын жылдамдық та артады. Енді қаншасыншы N-нен бастап Dareje функциясы жылдам жұмыс істейтінін қарастырайық.

Әрбір циклда негізгі уақыт көбейтуге кететіндіктен ТС ₁ ≈Т ₁ ≈Т ₂ деп есептеуге болады. Бұдан,

Т(N) ≤ ТС ₁ ·(2∙ [log ₂ N] +1)

екені шығады. 2∙ [log ₂ N] +1<N теңсіздігін шеше отырып, N>5 екенін табамыз. N-нің шекаралық мәнін іздеуде T(N) үшін жоғарыдан бағалауды пайдаландық. N-нің 1-ден 5-ке дейінгі мәндерін жеке зерттеуге болады. N=1, 2, 3 мәндері үшін Dareje функциясы tyzusyzykty функциясы тәрізді көбейтуді орындайды, ал N=4, 5 мәндерінде көбейту аз орындалады. Бұл N-нің барлық мәндері үшін Dareje функциясын пайдалануға болатынын көрсетеді.

Талдауды қорытындылайтын болсақ, егер FOR циклында қайталану саны айнымалы болып, программада есептелсе онда, жұмыс уақытын бағалауға формальды әдістерді қолдануға келмейді, программа жұмысын мазмұнды талдауды талап етеді. Ал, While-Do және Repeat-Until қайталанулар одан да үлкен қиындық әкеледі. Бұл қайталанулар үшін қайталанудың жалпы формуласын жазуға келмейді. Бұдан барлық уақытта барлық қиындықтарды жеңіп, жұмыс уақытын есептеудің жуықтатылған формуласын табу мүмкін бола бермейді. Алгоритмді бағалауда кейде құрғақ ақпаратпен шектелуге тура келеді. Мұндай жағдай барлық мүмкін болатын көбейткіштерді таңдауға негізделген санды қарапайым көбейткіштерге жіктеу алгоритмінде орын алады. Сонымен бірге, сан жай сан болса, таңдауды соңына дейін жүргізуге тура келеді, алдымен санның жай сан екеніне көз жеткізу қажет. Бұл алгоритм үшін жұмыс уақытын жоғарыдан бағалау міндеті қойылады, осындай TMAX(N) шамасы N өлшемді есеп үшін шынайы жұмыс уақыты TMAX(N) -нан артпайды және кейде осы шаманың өзіне тең болады. Жұмыс уақытын есептеуге арналған формуламен алгоритмді салыстырумен қатар, өлшенген жұмыс уақытын басқа есептің өлшеміне экстрополяциялау үшін пайдалануға болады. Мысалы, 2 ¹ дәрежесін есептеу қажет болсын. Мұның едәуір уақыт алатынын алдын-ала айтуға болады. Ол үшін 2 ¹⁰⁰⁰ дәрежесін есептеп, есептеу уақытын өлшейміз. Мысалы, ол 30 секундқа тең болсын. Онда 2 ¹ -ін есептеу 10*10=100 есе көп болады, 3000 секундты, яғни 50 минутты құрайды. Бұл 2 ¹ дәрежесін есептеу одан да жылдам алгоритм іздеуді талап етеді.

Рекурентті тізбектерді өңдеу

U(1), …, U(K) тізбегінің алғашқы К-сыншы мүшелері берілген болса, онда U(1), U(2), …, U(N) тізбегінің элементтері К ретті рекурентті тізбекті құрайды делінеді, ал N>К үшін

U(N) =F(U(N-1), …, U(N-K) )

теңдеуi орындалады. Мұндағы Ғ - К аргументтің қандай да бір функциясы. Екінші ретті пекуррентті тізбекті белгілі мысалы Фибоначчи сан тізбегі болып табылады., оның

U(1) =U(2) =1, ал N>2 үшін

U(N) =U(N-1) +U(N-2) .

Бірінші ретті рекуррентті тізбектің мысалы - а санынан квадрат түбірді Ньютон әдісі бойынша есептеуге арналған тізбек: U(1) =a+1, ал N>1 үшін

U(N) =0. 5*(U(N-1) +a/U(N-1) ) .

Рекуррентті тізбектерге қатысты төмендегідей есептер қойылады.