Есептеу математикасындағы қателіктердің жіктелуі: жуықтау, дөңгелектеу және абсолютті-салыстырмалы қателіктер


Қателіктердің жіктелуі.
Ғылым мен техникада көптеген есептер функциялар, алгебралық, дифференциалдық немесе интегралдық теңдулер арқылы математика тілінде сипатталып жазылады. Мұндай есептер түрліше жолдармен шешіледі. Анализдік әдістер сондай жолдардың бірі болвп табылады. Бірақ оларды пайдалану көп жағдайда мүмкін бола бермейді.
Кейінгі 30-40 жыл ішінде жылдам есептейтін электрондық есептеуіш машиналар (ЭЕМ) кеңінен қолданылып келеді. Олардың кейбіреулері секундына жүздеген миллионға дейін арифметикалық амалдар орындайды. Сонымен бірге машиналарда есептеулерді жеңілдететін басқа да қосымша мүмкіншіліктері бар. Электрондық есептеуіш машиналардың пайда болуы есептеу математикасының қарқынды дамуына зор әсерін тигізгенін айта кеткен жөн.
Есептеу кезінде анализдік әдістерді пайдалану қиындық келтіргенде немесе тіпті пайдалану мүмкін болмаған жағдайда есептеу математикасының сандық әдістері қолданылады. Ол әдістер бастапқы берілген есепті мағынасы бойынша соған жуық басқа есеппен алмастыру мүмкіндігіне негізделген. Ал соңғы есеп кейбір шарттарды қанағаттандыру тиіс. Мәселен, шешімінің бар болуы, орнықты, жинақты болуы және т. с. с. Бұл есептің шешімі алғашқы есептің жуық шешімін беруі тиіс немесе оған белгілі бір дәлдікпен жинақталуы қажет.
Дәл және жуық шешімдердің айырымын жуықтау немесе әдіс қателігі деп атайды.
Есепте негізгі деректер, яғни ондағы коэффициенттер, бос мүшелер немесе қосымша шарттар жуық шамалармен берілуі мүмкін, соның нәтижесінде пайда болған қателіктерді жөнделмейтін (түзетілмейтін) қателіктер деп атайды.
ЭЕМ-де цифрлар саны шексіз көп сандарға арифметикалық амалдар қолданылмайды. Сондықтан ондай сандар ең алдымен цифрларының саны шектеулі жуық сандармен алмастырылады. Ол, әдетте, орта мектептен белгілі дөңгелектеу әдісі арқылы жүзеге асырылады. ЭЕМ-де дөңгелектеу амалы арифметикалық амалдар орындалған кездерде де жүргізіледі. Өйткені нәтижеде цифрларының саны шексіз көп сандар пайда болуы мүмкін. Осындай дөңгелектеулердің салдарынаң пайда болған қателіктерді есептік қателіктер деп атайды. Олар есептің жуық шешімінің дәлдігіне тікелей әсерін тигізетіні анық.
Жуық сандардың жөнделмейтін және есептік қателіктеріне осы рефератта тоқталамыз.
Сандарды ЭЕМ-де жазу
p негізгі санау жүйесінде (p-кез-келген бүтін оң сан) N p саны
N p =±mp ±q (1)
түрінде жазылады. Мұнда m және q- N p санының мантиссасы және реті болып табылады.
Санның жоғарыда көрсетілген түрінде кескінделуін оның жылжымалы үтір түріндегі жазылуы деп атайды. Бұлай аталу себебін жоғарыда байқауға болады.
Ал дербес жағдайда m мантисса үшін
 (2)
(2)
шарты орындалса, онда (1) формуласы санның нормаль түрі деп аталады.
ЭЕМ-нің көпшілігі екілік жүйеде нормаль түрде жазылған сандармен ғана жұмыс істейді. Ол сандар үшін (2) шарты

түрінде жазылады.
Әрбір сан ЭЕМ-нің белгілі бір ұяшығына орналасады. Олардың құрылым жүйесінде m және q мәндеріне арналған саны шектеулі екілік разрядтар бөлінген.
Айталық, ұяшықта m мантисса үшін t екілік разряд бөлінген болсын. Онда N 2 саны мына түрде өрнектеледі:
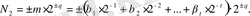
Мұндағы
 коэффициенттері 0-ге немесе 1-ге тең.
коэффициенттері 0-ге немесе 1-ге тең.
Жуық сандардың абсолют және салыстырмалы қателіктері
Айталық, x берілген санның дәл мәні, ал
 оның жуық мәні болсын. Кейде
оның жуық мәні болсын. Кейде
 жуық санының бірнеше мәндері болуы мүмкін.
жуық санының бірнеше мәндері болуы мүмкін.
Әдетте,
 шамасын
шамасын
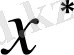 жуық санының абсолют қателігі деп атайды. Қарастырылып отырған санның x дәл мәні көбінесе белгісіз болады. Сондықтан
жуық санының абсолют қателігі деп атайды. Қарастырылып отырған санның x дәл мәні көбінесе белгісіз болады. Сондықтан
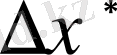 қателігі анықтала бермейді. Бірақ оны жоғарыдан шектейтін шаманы әруақытта көрсетуге болады.
қателігі анықтала бермейді. Бірақ оны жоғарыдан шектейтін шаманы әруақытта көрсетуге болады.
1-анықтама. Есептеу математикасында
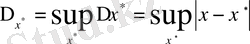
шамасын
 жуық санының
шектік абсолют қателігі
деп атайды.
жуық санының
шектік абсолют қателігі
деп атайды.
Бұл анықтамадан
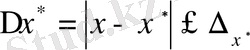
екені анық. Демек,
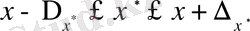 .
.
2-анықтама.
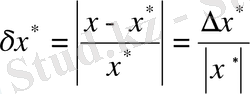
шамасын
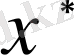 жуық санының
салыстырмалы қателігі
деп аиайды.
жуық санының
салыстырмалы қателігі
деп аиайды.
Ал жуық санның шектік салыстырмалы қателігі мына формуламен анықталады:
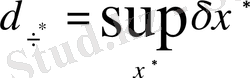 .
.
2-анықтамадан
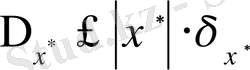 теңсіздігі шығады. Жалпы
теңсіздігі шығады. Жалпы
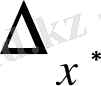 шектік абсолют қателік пен
шектік абсолют қателік пен
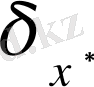 салыстырмалы қателіктер арасында мынадай байланыс бар:
салыстырмалы қателіктер арасында мынадай байланыс бар:
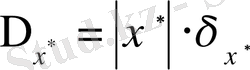 .
.
Бұдан
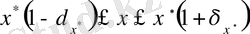
теңсіздігін алуға болады, яғни
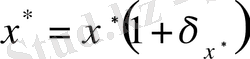 .
.
Практикада жуық санның салыстырмалы қателіктері көбіңесе процентпен беріледі.
Электрондық есептеуіш машиналар жадына сандарды енгізгенде пайда болатын абсолют және салыстырмалы қателіктердің шамаларын анықтайық. Мысалы,
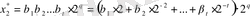
болсын делік. Онда бұл санның шектік абсолют қателігі соңғы бірлік разрядтан асып кетпейтіні мәлім, яғни
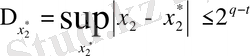 .
.
Ал
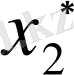 жуық санының шектік салыстырмалы қателігі үшін
жуық санының шектік салыстырмалы қателігі үшін
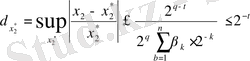
Теңсіздігі орындалады. Бұдан
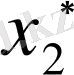 жуық санының,
жуық санының,
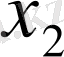 дәл мәні үшін
дәл мәні үшін
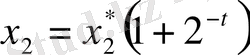
формуласын шығарып алуға болады.
Ондық санау жүйесінде кез-келген
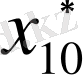 саны
саны

Түрінде жазылады. Мұндағы
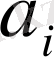 коэффициенттері 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, сандарының біреуіне тең.
коэффициенттері 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, сандарының біреуіне тең.
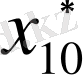 жуық санының өрнектклуіндегі бірінші
жуық санының өрнектклуіндегі бірінші
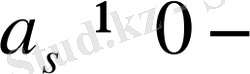 ден басталған барлық
ден басталған барлық
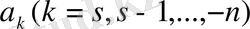 коэффициенттері оның
мәнді цифрлары
деп аталады.
коэффициенттері оның
мәнді цифрлары
деп аталады.
Егер
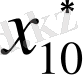 санының абсолют қателігі
санының абсолют қателігі
 цифрына сәйкес келетін k бірлік разрядының шамасынан
цифрына сәйкес келетін k бірлік разрядының шамасынан
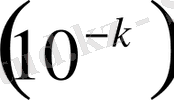 аспаса, онда
аспаса, онда
 дұрыс цифр
, ал кері жағдайда
күмәнді цифр
деп аталады.
дұрыс цифр
, ал кері жағдайда
күмәнді цифр
деп аталады.
Жуық сандарды жазған кезде оның цифрлары дұрыс болуы тиіс. Сонда санның жазылуы бойынша оның қателігін анықтау қиын емес. Кейде есептік қателіктер көбеймеу үшін, жуық санның жазылуында 1-2 күмәнді цифрлар сақталып жазылады.
Жуық шаманың салыстырмалы қателігі оның үтірден кейінгі дұрыс цифрларының саны арқылы анықталады. Мәселен үтірден кейін бір дұрыс цифр болса, онда оның салыстырмалы қателігінің шамасы сол санның 10%-не, екеу болса, 1%-не, ал үшеу болса, 0, 1%-не тең болады.
Дөңгелектеу қателіктері.
ЭЕМ-дер разрядтарының саны шектеулі сандармен ғана жұмыс істей алатыны белгілі. Оларға арифметикалық амалдарды қолданғанда, разрядтарының саны өте көп сандар пайда болуы ғажап емес. Сонымен қатар, есептеу нәтижесі машинаның ұяшығына сыймауы да мүмкін. Бұл жағдайда дөңгелектеу арқылы ол басқа жуық санмен алмастырылады. Енді осы амалға тоқталайық. Түсінікті болуы үшін ондық жүйедегі сандарды қарастырайық.
Айталық,
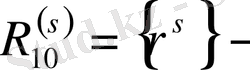 разрядтарының саны s-тен аспайтын ондық сандар жиыны болсын. Бұл жиынның кез-келген
разрядтарының саны s-тен аспайтын ондық сандар жиыны болсын. Бұл жиынның кез-келген
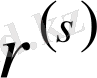 мүшесі мына түрде жазылады:
мүшесі мына түрде жазылады:
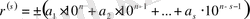
Мұндағы
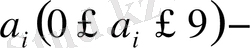 ондық цифрлар. Есептеу барысында
ондық цифрлар. Есептеу барысында
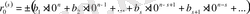
саны пайда болды делік. Ол
 немесе
немесе
 шарттарының біреуін ғана қанағаттандырады. Соңғы жағдайда
шарттарының біреуін ғана қанағаттандырады. Соңғы жағдайда
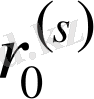 орнына басқа
орнына басқа
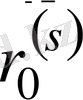
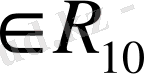 жуық саны алынады. Ол төмендегіше жүзеге асырылады:
жуық саны алынады. Ол төмендегіше жүзеге асырылады:
а) егер
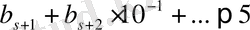 болса, онда
болса, онда
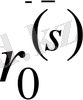
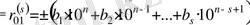 деп алынады;
деп алынады;
б)
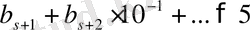 болса, онда
болса, онда

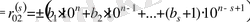 деп алынады;
деп алынады;
в)
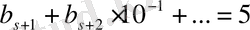 болып,
болып,
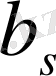 жұп болса, онда
жұп болса, онда
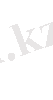
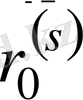 =
=
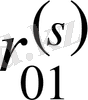 , ал кері жағдайда
, ал кері жағдайда
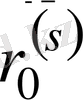 =
=
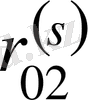 деп алынады.
деп алынады.
Енді жуық санды дөңгелектегенде, оның абсолют қателігі қалай өзгеретінін анықтайық. Айталық,
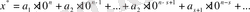
Жуық санын жоғарыдағы ереже бойынша s разрядқа дейін дөңгелектеп
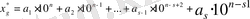
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz