Жылжымалы үтірлі сандарды екі разряд бойынша талдап көбейтуге арналған синхронды басқарушы автоматты синтездеу


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 24 бет
Таңдаулыға:
Кіріспе
Бұл курстық жобада жылжымалы үтірлі сандарды екі разряд бойынша талдап көбейту операциясын орындайтын басқарушы автомат синтезделеді. Тексеру модуль бойынша жүргізіледі. Негізгі мақсаты - БА-тың функционалдық сұлбасын құру. Функционалдық сұлбаны құру үшін “ЖӘНЕ-НЕМЕСЕ” логикалық элементтер және жады элементі ретінде Т триггер қолданылады.
Курстық жоба 2 бөлімнен тұрады: операция орындалуының алгоритмін құру және осы алгоритмді жүзеге асыратын БА синтездеу. Сонымен қатар, осы тәсілді жүзеге асыратын программа жазу керек.
1. Операция орындалуының алгоритмін құру.
1. 1 Жылжымалы үтірлі сандарды кіші разряд бойынша талдап көбейту .
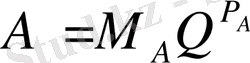 мен
мен
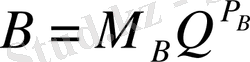 сандарының көбейтіндісі мынаған тең:
сандарының көбейтіндісі мынаған тең:
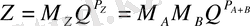 . Бұдан көбейтіндінің реті
. Бұдан көбейтіндінің реті
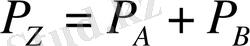 , ал мантиссасы
, ал мантиссасы
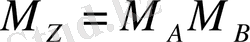 екені көрініп тұр. Мантиссаларды көбейту табиғи түрде көрсетілген тиянақты үтірлі сандарды көбейтуге ұқсас. Көбейтіндінің реті көбейткіштер реттерін қосу арқылы анықталады. Ауытқыған реттердің қосқанда мынаны еске алу керек:
екені көрініп тұр. Мантиссаларды көбейту табиғи түрде көрсетілген тиянақты үтірлі сандарды көбейтуге ұқсас. Көбейтіндінің реті көбейткіштер реттерін қосу арқылы анықталады. Ауытқыған реттердің қосқанда мынаны еске алу керек:
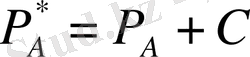 ,
,
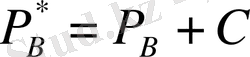 және
және
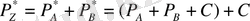 мұнда ауытқыған реттер қосындысы С мәніне артық, сондықтан одан С мәнін шегеру керек:
мұнда ауытқыған реттер қосындысы С мәніне артық, сондықтан одан С мәнін шегеру керек:
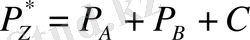 .
.
Жалпы алғанда көбейту операциясы мынандай кезеңдерден тұрады: 1. көбейтінді таңбасы А мен Б сандары таңбаларын екі модуль бойынша қосындылау арқылы анықталады; 2. көбейтіндінің реті анықталады; 3. көбейтіндінің мантиссасы есептеледі; 4. нәтиже қалыпталынады.
Жылжымалы үтірлі сандарды көбейткенде мына кезеңдерді еске алу керек: 1. егер көбейгіштердің мантиссалары 0-ге тең болса, онда нәтижеге операцияның орындамай-ақ 0 мәні меншіктеледі; 2. егер реттер қосындысын анықтау үстінде теріс таңбалы аса толу пайда болса, онда мантиссаларды көбейтпей-ақ нәтижеге 0 мәні меншіктеледі; 3. егер реттер қосындысы анықтағанда оң таңбалы аса толу алынса, онда мантиссаларды көбейтуге кіріседі: мантиссаларды көбейткен соң қалыптану оңға қарай бұзылуы мүмкін, мантиссаны қалыптылағаннан кейін ретте аса толу жоюлуы мүмкін.
Мантиссаларды көбейту.
Адыңғы разрядтар жұптарының кіші разрядтарына келетін тасымалды ескеріп, көбейткіштің екі разрядына қосындыны жылжыту және 1, 0 цифрлары жүйесіне көшу арқылы көбейту әдісін қарастырдым.
Көбейткіштің екі кіші разрядтар тобының мәндері мынандай болуы мүмкін: 00, 01, 10, 11.
Екі разряд мәні 00 болғанда көбейгіш КБҚ-ға қосындыланбай, КБҚ оңға қарай екі разрядқа жылжытылады. Екі разряд мәні 10 болса, екі еселенген көбейгіш КБҚ- ға қосындыланып, содан соң КБҚ оңға екі разрядқа жылжытылады. 01 комбинациясында КБҚ -ға көбейгіш қосылып, қосынды оңға екі разрядқа жылжытылады. Егер талданатын разрядтар тобының мәні 11 болса, онда 11= 1000-001=101 түрінде қаралады. Онда тасымал осынща жады элементінде сақталады, ал КБҚ -дан көбейгіш азайтылады да, нәтиже оңға қарай екі разрядқа жылжытылады.
Бұл әдіспен көбейткенде төменгі қос разрядтан берілетін тасымал түзету тіркегішінде (ТТР) сақталады да, көбейткіштің келесі қос разрядын талдағанда ескеріледі. ТТР 1 болғанда, егер келесі қос разрядтар мәні 00 болса, онда оларды 01 деп, ал 01 болса, онда - 10 деп, 10 болса - 11 деп, 11 болса - 00 деп қараймыз. Соңғы екі комбинацияда бірлік ТТР -де сақталады. 1-ші таблицада төменгі қос разрядтар ауысатын тасымал мәні ескеріліп көбейткіштің төменгі екі разрядын талдау ережесі келтірілген. 1-кесте
Реттерді қосындылау.
Рх және Ру реттерін алгебралық қосындылағанда шағатын нәтиже Pz -нің бес жағдайын орнатуға болады.
1.
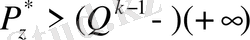
2.
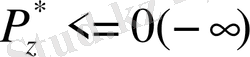
3.
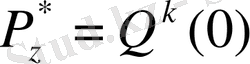
4.
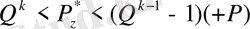
5.
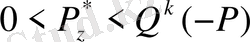
Мұндағы К реттердің разрядтылығы
1. жағдайда оң аса толу жағдайы орын алады. Бұл жағдайда реттер операцияға оң таңбамен қатысады. Егер реттер операцияға теріс таңбамен қатысса онда 2-ші жағдай орындалады. Бұл жағдайда теріс таңбалы аса толу алынады.
3-ші жағдай орын алады, егер операцияға қатысатын реттердің таңбалары әртүрлі болып, модулдері бірдей болса. 4-ші және 5-ші жағдайлар реттердің (Pz мәні реттердің разрядтық торының шекарасында болса) таңбалары әртүрлі болғанда орын алады.
4-ші жағдай орын алады, егер реттердің алгебралық қосындысының нәтижесі Pz оң таңбалы (+Р) болса. 5-ші жағдай орын алады, егер реттердің алгебралық қосындысының нәтижесі Pz теріс таңбалы (-Р) болса.
Алуда жылжымалы үтірлі сандардың реттерімен операцияларды орындағанда әрі қарай әрекеттерді орындау үшін осы бес жағдайды қарастыру қажет.
1. 2Жылжымалы үтірлі сандарды кіші разряд бойынша талдап
көбейтуге мысал.
[X] ТУРА =0 010
[Y] ТУРА =-0 1011
Шешеуі:
а) Көбейтіндінің таңбасын анықтаймыз:
Т1+Т2=0+1=1
б) Реттерін есептейміз:
Р X * = 0100
+
P Y * = 0101
P X * +Р Y * = 1001
в) Мантиcсаларды көбейтеміз:
010
01
01 R(5)
010
1 11101
011110100 R(2)
010
- 0011101001110100
1001110100111010 R(1)
Z=0, 1001110100111010
г) Нәтижені қалыптастырамыз, ол үшін M Z бір разрядқа солға жылжытамыз да P Z * -тен. Сонда нәтиже мына түрде болады:
Z=1 000 0110.
1. 3 Операциялы автоматтың құрылымы .
Операциялық автоматты құру үшін Т тригерін және “И - ИЛИ” логткалық элементтерін пайдаландық. Осы элементтер арқылы Мили автоиатының құрылымын құрдық. Операциялық автоматтың құрылымын анықтау үшін қажет ригистрлердің санын және олардың разрядтылығын анықтау керек. Берілген алгоритмді пайдаланып, көбейтуді орындау үшін мыналар қажет болады:
- Бірінші көбейткішке арналған алты разрядты бір регистр.
- Екінші көбейткішке арналған алты разрядты бір регистр.
- Көбейтіндіге арналған он екі разрядты бір регистр.
- Он екі разрядты сумматор.
- Бірінші ретке арналған төрт разрядты регистр.
- Екінші ретке арналған төрт разрядты регистр.
- Төрт разрядты сумматор.
- Алты разрядты счетчик
1. 4 Программаның сипаттамасы
Програма, Delphi-6 программалау тілінде жазылған. Бұл программаның аты АЛУ. Программаны орындау үшін АЛУ. dfm файлын іске қосу керек. Программа арнайы процедураларды шақыру арқылы орындалады.
Программаның листингісі А-қосымшасында келтірілген.
Программада қолданылданылған процедуралар:
Draw процедурасы
Solve процедурасы
Inv процедурасы
Add процедурасы
Valu процедурасы
Proc процедурасы
Norm процедурасы
1. 5 Қолданушыға нұсқау
Бұл программаны жұмыс істету Delphi-да Ctrl+F9 пернелерін басамыз.
1. 6Программаның алгоритмі
1. 7Операция орныдалуының уақытын және операциялық автоматтың (ОА) аппараттық шығындарын есептеу.
Операция орындалуының уақыты - уақыт бірлігімен есептелнеді, себебі операцияның орындалуы қосу және жылжыту микрооперациялардың орындалуынан тұрады. Сонымен уақыттың шартты бірлігі деп, бір екілік разрядқа (τ ж ) жылжыту микрооперациясын орындауға кеткен уаөытты айтамыз. Сонымен қосу микрооперациясын орындауға кеткен уақыт төрт жылжыту операцияларға тең болады:
τ қосу = 4τ ж .
Операциялық автоматта операцияны орындауға кеткен уақыт мынаған тең болады:
τ = n(T қосу + T ж ) + T қ1 +Рт T ж
Бұл жерде n - разряд саны
T қ - қосу уақыты (4T қ )
T қ1 - тәртіпті қосу
Рт T ж - түзету (0, 5)
Ақпараттық шығындар.
Q ОА = Q Рг1 + Q Рг2 + Q Рг3 + Q СМ = 16 + 8 + 8 + 5 + 5 + 5 + 8 +5=55ж. э.
ОА-ның ақпараттық шығандар жады элементінің шартты бірлігімен яғни, тригерлермен есептелнеді. Бұл кезде логикалық элементтер ескерілмейді.
1. 8 Операция орындалуын бақылау.
Модуль бойынша бақылауда сан кодына қосымша бақылау разрядтары енгізіледі. Олраға берілген белгілі бүтін санға бөлу жолымен алынған қалдық жазылады. Мүндай кодта машиналық сан шартты түрде бүтін сан түрде қаралады. Берілген ақпараттармен қандай операция жүргізілсе қалдықтармен сондай операциялар жүргізіледі. Қалдықтармен жүргізілген операциялар нәтижесі бақылауға тиісті операция нәтижесінде берілген модульге бөліну арқылы алынған қалдыққа тең болу керек. Қалдықтар (Р) бір - бірімен тең болмаса, онда ол жіберілген қателік белгісі болып табылады. Бұл тәсілмен модуль мөлшері не еселі емес барлық қателерді табуға болады.
Модуль мөлшеріне мынандай талаптар қойылады: 1. модульдің көптеген қателерді табу мүмкіндігі болу керек; 2. қалдық бөлу амалы орындалуын талап етпейтін қарапайым жолмен табылуы керек; 3. модуль мөлшері және ол арқылы алынған қалдық разрядтылығы үлкен болмау керек.
А = 0. 010
В = -0. 1011
Z = -0. 1001110100111010
X (mod 3) = 01
A mod3 =01
B mod3 =10
Z mod3 =10
A mod3 * B mod3 ==01*10=10
10===10>> дұрыс
Модуль бойынша бақылау көрсеткеніндей нәтиже дұрыс шықты.
2. Басқару автоматын синтездеу.
2. 1 Микропрограмманы кодалау .
Алгоритмнің граф схемасы (АГС) бойынша микропрограммалық автоматты синтездеуге көшейік. Мили автоматын синтездеу кезінде белгіленген АГС алу былай жүзеге асырылады: а) бастапқыдан кейінгі төбенің кірісімен соңғы төбе кірісі а 1 сигналымен белгіленеді; б) операциялық төбелерден кейінгі төбелер кірісі а 2 , а 3 , . . . , а n белгіленеді . ; в) белгіленітін төбелердің кірістері әртүрлі символдармен белгіленеді және бір реттен артық емес. Пайдаланатын символдар санын синтезделінетін автоматтың А= { а 1 , а 2 , . . . , а n } күйлер алфавиті анықтайды.
Жоғарыда айтылған ережелерді пайдаланып, белгіленген ГСА - ны аламыз (қосымша Б)
2. 2 Микропрограммалық автоматтың құрылымдық кестесін құру
Берілген типті автоматты синтездеу үшін берілген АГС бойынша құрылған МПА - ның құрылымдық тура кестесін құру керек. Бұл жағдайда Мили МПА - ның көшу кестесінде жеті бағана болады: а м - бастапқы күй; к(а м ) - бастапқы күйінің екілік коды; х(а м , а s ) - а м күйінен а s күйіне көшуге себепші болатын енгізу сигналы. Y(а м , а s ) - берідген көшуге сәйкес шығару сигналы; F(а м , а s ) - МПА - ны а м күйінен а s күйіне көшіруге қажетті жады элементтерінің қозу сигналдары.
 X
2
X
2
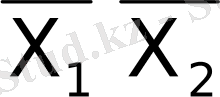

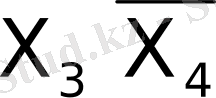
 X
5
X
5

 X
6
X
6










 X
8
X
8



2-кесте бойынша автоматтың қозу функцияларын жазамыз:
S1=A
1
V A
1
X
7
 V A
10
X
7
X
8
V A
10
X
7
X
8
 VA
16
VA
16
 VA
16
X
8
VA
16
X
8

S2=A
1
VA
11
X
6
VA
11

S3=A
3
 X
2
VA
3
X
2
VA
3

 VA
4
X
2
VA
4
VA
4
X
2
VA
4
 VA
10
VA
10
 VA
13
X
5
VA
13
VA
13
X
5
VA
13

S4=A
4
 VA
5
VA
10
X
7
X
8
VA
5
VA
10
X
7
X
8
 VA
12
VA
15
X
5
VA
15
VA
12
VA
15
X
5
VA
15
 X
8
X
8

R1=A
6
X
3
 VA
6
VA
6
 X
5
VA
6
X
5
VA
6

 X
6
VA
6
X
6
VA
6


 VA
12
VA
13
X
5
VA
12
VA
13
X
5
R2=A
6
X
3
 VA
9
VA
9
R3= A
6
X
3
 VA
6
VA
6


 VA
7
VA
7
 VA
8
VA
11
VA
8
VA
11
 VA
15
VA
15


 VA
16
VA
16
 VA
16
X
8
VA
16
X
8

R4= A
3
 V A
3
V A
3

 VA
6
VA
6

 X
6
VA
6
X
6
VA
6


 VA
7
VA
7
 VA
13
VA
13
 VA
14
VA
16
VA
14
VA
16

Автоматтың күйлер кодтарын минимизациялау үшін, Вейч-Карно диаграммасын пайдаланамыз (3-кесте) .
S1=A
1
& A
1
X
7
 & A
10
X
7
X
8
& A
10
X
7
X
8
 &A
16
&A
16
 &A
16
X
8
&A
16
X
8

S2=A
1
&A
11
X
6
&A
11

S3=A
3
 X
2
&A
3
X
2
&A
3

 &A
4
X
2
&A
4
&A
4
X
2
&A
4
 &A
10
&A
10
 &A
13
X
5
&A
13
&A
13
X
5
&A
13

S4=A
4
 &A
5
&A
10
X
7
X
8
&A
5
&A
10
X
7
X
8
 &A
12
&A
15
X
5
&A
15
&A
12
&A
15
X
5
&A
15
 X
8
X
8

R1=A
6
X
3
 &A
6
&A
6
 X
5
&A
6
X
5
&A
6

 X
6
&A
6
X
6
&A
6


 &A
12
&A
13
X
5
&A
12
&A
13
X
5
R2=A
6
X
3
 &A
9
&A
9
R3= A
6
X
3
 &A
6
&A
6


 &A
7
&A
7
 &A
8
&A
11
&A
8
&A
11
 &A
15
&A
15


 &A
16
&A
16
 &A
16
X
8
&A
16
X
8

R4= A
3
 & A
3
& A
3

 &A
6
&A
6

 X
6
&A
6
X
6
&A
6


 &A
7
&A
7
 &A
13
&A
13
 &A
14
&A
16
&A
14
&A
16

Т-триггерлерді және логикалық ЖӘНЕ, НЕМЕСЕ элементтері пайдаланатын 1-кестемен берілген МПА схемасы Б-қосымшада кескінделген.
3. Техникалық құрал жабдықтар.
Бұл программаны іске қосу үшін WINDOWS операциялық жүйесі бар IBM PC/XT дербес компьютер болса жеткілікті.
Оперативті жадының 2. 47Мб көлемі қажет.
Қорытынды
Берілген курстық жобада басқарушы автомат синтезделді. Ол екілік кодында берілген екі жылжымалы үтірлі сандарды екі разряд бойынша талдап көбейту тәсілін пайдаланыпб көбейту операциясын басқарды.
“И - ИЛИ” базисында және Т - триггерлер негізінде жасалған синхронды басқарушы Мили автоматы құрылды. Бұл курстық жобада қолданылған алгоритм Delphi 7. 0 тілінде жазылған программа арқылы тексерілді.
Қолданылған әдебиеттер
- Айтхожаева Е. Ж., Тынымбаев С. Т.
«Арифметические и логические устройства ЭВМ».
- Савельев А. Я.
Прикладная теория цифровых автоматов: Учеб. для вузов по спец. ЭВМ. - М. : Высш. школа, 1987. - 272 стр.
- Тынымбаев С. Т.
Вычислительные машины, системы, комплексы и сети. Учебник для вузов. - Алматы: Рауан, 1996 г.
- Айтхожаева Е. Ж., Тынымбаев С. Т.
Цифрлық автоматтардың қолданбалы теориясы: Оқулық - Алматы: Рауан, 1992ж.
Қосымша А
Uses crt, graph;
Var
Gm, Gs:integer;
hf:array[-7. . 7] of string;
st1, st2, st3, st, sta, stb, stc, sig:string;
a, b, c:array[0. . 13] of shortint;
i, j, k, uz, cx, uz2, s, sub:integer;
x, x1, x2, p, p2, op1:string;
op:array[1. . 8] of string[3] ;
Procedure draw;
begin
setcolor(15) ;
rectangle(40, 40, 150, 51) ; {recx}
line(50, 40, 50, 51) ;
line(20, 240, 65, 240) ;
line(10, 251, 75, 251) ;
line(10, 251, 20, 240) ;
line(65, 240, 75, 251) ;
line(44, 240, 44, 230) ;
line(44, 230, 155, 230) ;
line(44, 251, 44, 261) ;
circle(44, 263, 2) ;
line(44, 265, 44, 278) ;
line(44, 278, 42, 273) ;
line(44, 278, 46, 273) ;
outtextxy(42, 279, 'x5') ;
line(60, 75, 120, 75) ; {mover}
line(50, 86, 60, 75) ;
line(130, 86, 120, 75) ;
line(50, 86, 130, 86) ;
line(118, 103, 136, 103) ; {arrow1 to a mover}
line(117, 103, 122, 101) ;
line(117, 103, 122, 105) ;
outtextxy(144, 100, 'y7') ;
circle(138, 103, 2) ; {bulb needed}
line(114, 110, 132, 110) ; {arrow2 to a mover}
line(113, 110, 118, 108) ;
line(113, 110, 118, 112) ;
outtextxy(138, 109, 'y8') ;
circle(134, 110, 2) ;
line(60, 100, 120, 100) ; {tur}
line(50, 111, 110, 111) ;
line(50, 111, 60, 100) ;
line(120, 100, 110, 111) ;
line(130, 75, 130, 86) ;
line(130, 77, 140, 77) ;
line(144, 77, 148, 77) ;
line(130, 77, 135, 75) ;
line(130, 77, 135, 79) ;
circle(142, 77, 2) ;
outtextxy(150, 73, 'y5') ;
line(130, 84, 140, 84) ;
line(144, 84, 148, 84) ;
line(130, 84, 135, 82) ;
line(130, 84, 135, 86) ;
circle(142, 84, 2) ;
outtextxy(150, 84, 'y6') ;
line(85, 86, 85, 100) ; {1/2-den tur}
line(85, 100, 83, 95) ;
line(85, 100, 87, 95) ;
line(85, 111, 85, 137) ; {tur sum1}
line(85, 137, 83, 132) ;
line(85, 137, 87, 132) ;
line(90, 75, 90, 51) ; {arrow above the mover}
line(90, 75, 88, 70) ;
line(90, 75, 92, 70) ;
rectangle(180, 40, 290, 51) ; {recy}
line(190, 40, 190, 51) ;
line(273, 49, 273, 55) ; {arrow to x1}
line(273, 59, 273, 63) ;
line(273, 63, 283, 63) ;
circle(273, 57, 2) ;
line(283, 63, 278, 61) ;
line(283, 63, 278, 65) ;
outtextxy(285, 60, 'x1') ;
line(285, 49, 285, 55) ; {arrow to x0}
line(285, 55, 290, 55) ;
circle(292, 55, 2) ;
line(294, 55, 310, 55) ;
line(310, 55, 305, 53) ;
line(310, 55, 305, 57) ;
outtextxy(312, 51, 'x0') ;
line(35, 10, 530, 10) ; {line over recs}
line(35, 11, 530, 11) ;
line(45, 51, 45, 137) ;
line(43, 132, 45, 137) ; {arrow1 to summator1}
line(45, 137, 47, 132) ;
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz