Конденсатор және оның түрлері мен қолданулары

Пән: Физика
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:

Қазақстан Республикасының білім және ғылым министрлігі

Құдайберген Жұбанов атындағы Ақтөбе мемлекеттік университеті

Кафедрасы: Эксперименттік және теориялық физика кафедрасы

Факультеті: Физика - математика

Курстық жұмыс

Тақырыбы:

Конденсатор және оның түрлері мен қолданулары

Орындаған: 2фқб тобы студенті Жағыпарова Ш. Б.

Тексерген: ЭТФ кафедрасының доценті Жұбаев А. Қ.

Ақтөбе 2012жыл.

Жоспар:

I. Кіріспе . . . 3

II. Негізгі бөлім . . . 4

2. 1. Конденсатор туралы жалпы ұғымдар . . . 4

2. 2. Конденсатордың сыйымдылығы . . . 5

2. 3. Конденсатордың типтері . . . 7

2. 4. Конденсаторларды қосу . . . 12

2. 5. Зарядталған конденсатордың энергиясы . . . 15

III. Қорытынды . . . 17

IV. Пайдаланған әдебиеттер . . . 18

Конденсаторлар барлық электр схемаларының таптырмайтын элементі болып табылады. Екі жарым ғасыр бұрын пайда болған конденсаторлар қазірде техниканың барлық саласында қолданыс тауып отыр. Практикада сонымен бірге өзін қоршаған денелермен салыстырғанда шамалы потенциалы бола тұрып шамасы едәуір зарядтарды жинақтайтын, яғни конденсациялайтын қондырғылар қажет болады. Конденсатор деп аталатын мұндай қондырғылар негізінен өткізгіштерге басқа денелерді жақындатқанда оның электр сыйымдылығы артатын фактіге суйенеді.

Бұл курстық жұмыстағы менің басты мақсатым - конденсаторлардың түрлі типтерімен танысып, электротехниканың қандай облыстарында қолданылатынын анықтау және конденсатор туралы өз білімімді толықтыру.

1745 жылы Лейден қаласында неміс физигі Эвальд Юрген фон Клейст және голланд физигі Питер ван Мушенбрук тарихта ең алғашқы конденсатор - «лейден банкасын» жасады.

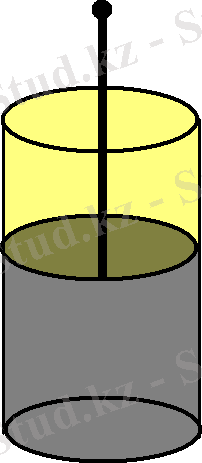
Конденсатор деп жұқа диэлектрик қабатымен бөлінген екі өткізгіштен тұратын жүйені айтамыз. Ол латынның “condenso”- қоюлату, жинақтау деген сөзінен шыққан. Конденсатор электр энергиясын және электр зарядтарын жинақтау үшін қолданылады. Конденсатордың екі өткізгішін оның жапсарлары деп атайды. Ол жапсарларды шамасы жағынан тең, таңбалары жағынан қарама -қарсы зарядпен зарядтайды. Бұл құрал өзіміз көріп жүрген телевизорларда, радиоқабылдағыштарда, магнитофонда және т. б электр құралдарында қолданылады.

300px-Defekte_Kondensatoren

Конденсатордын зарядты жинақтау қабілетін көрсететін физикалық шама - электрсыйымдылығы.

Өткізгіштің электрсыйымдылығы мынандай факторларға байланысты өзгереді:

Өткізгіштің электрсыйымдылығы оған екінші зарядталмаған өткізгішті жақындатқанда артады;
Екінші өткізгішті жерге жалғау бірінші өткізгіштің электрсыйымдылығын арттырады;
Қатты диэлектриктің болуы жүйенің электрсыйымдылығын арттырады;
Диэлектриктің қалыңдығын азайтса, өткізгіштер жүйесінің сыйымдылығы артады;
Диэлектриктің диэлектрик өтімділігі артқанда, жүйенің электрсыйымдылығы артады;
Өткізгіштердің бір-бірімен айқасу ауданын арттырғанда жүйенің электрсыйымдылығы артады.

Конденсаторларды сыртқы механикалық әсерлерден қорғау үшін оларды арнайы корпустармен қаптайды.

Конденсаторды схемада мына түрде белгілейміз:

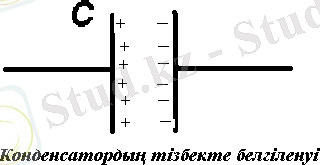
Халықаралық стандарт бойынша конденсаторларды жұмыс істеу принциптеріне байланысты тізбекте шартты түрде былай белгілейміз:

ГОСТ 2. 728-74

бойынша белгіленуі

Сипаттамасы

ГОСТ 2. 728-74бойынша белгіленуі: 1cm

Сипаттамасы: Тұрақты сыйымдылығы бар конденсатор

ГОСТ 2. 728-74бойынша белгіленуі: 1cm

Сипаттамасы: Поляризацияланған конденсатор

ГОСТ 2. 728-74бойынша белгіленуі: 1cm

Сипаттамасы: Айнымалы сыйымдылығы бар конденсатор

Сипаттық тағайындалуына қарай конденсаторларды шартты түрде жалпы және арнайы қолданыстағы конденсаторлар деп бөлуге болады Жалпы қолданыстағы конденсаторларға кең тараған төмен вольтты конденсаторлар жатады және олар құралдар мен аппараттардың көптеген түрлерінде қолданылады Ал қалған конденсаторлардың барлығы арнайы қолданыстағы конденсаторлар деп аталады. Оларға жоғарғы вольтты, импульстік, бөгетті жойғыш, дозиметриялық және т. б конденсаторлар жатады.

Конденсатордың негізгі сипаттамасы оның электрсыйымдылығы болып табылады. Ол конденсатордың электр зарядын жинақтау қабілетін көрсетеді. Сыйымдылықтың анықтамасы бойынша конденсатордың жапсарларындағы заряд оның жапсарларының арасындағы кернеуге тура пропорционал.

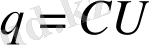
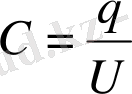
Конденсатордың сыйымдылығы әдетте 1 пФ -тан жүздеген мкФ -қа дейін, сонымен бірге сыйымдылығы ондаған Ф -қа дейінгі конденсаторлар да кездеседі.

Конденсаторларды жапсарларының пішініне қарай жазық, цилиндр тәріздес, шар тәріздес және т. б деп бөледі.

Жазық конденсатор . Егер өткізгіштер жазық болса және параллель орналасса, онда конденсатор жазық деп аталады. Жазық конденсатордың астарларының арасы, диэлектрик тұрақтысы $\varepsilon_{1}$ және $\varepsilon_{2}$ диэлектрик екі қабатпен толтырылған дейік; осы қабаттардың қалыңдықтары $d_{1}$ және $d_{2}$ болсын ;

Бұл жағдайда сыйымдылық былай анықталады:

С= $\frac{Q}{V_{1} - V_{2}}$ (2. 3. 1)

Алайда бұл жағдайда екі диэлектриктің шекарасы бар болып, сондықтан өріс кернеулігі бір диэлектриктен екінші диэлектрикке өткенде өзгеріске ұшырайды. Зарядталған астарлар арасындағы өріс кернеулігі бостықта $Е_{0}$ болсын, сонда:

$Е_{0}$ = 4πσ.

Диэлектриктердегі $Е_{1}$ мен $Е_{2}$ кернеуліктер сәйкесінше мынаған тең болады:

$Е_{1}$ = $\frac{4\pi\sigma}{\varepsilon_{1}}$ = $\frac{Е_{0}\ }{\varepsilon_{1}}$ , $Е_{2}$ = $\frac{4\pi\sigma}{\varepsilon_{2}}$ = $\frac{Е_{0}\ }{\varepsilon_{2}}$ .

Астарлардың біреуіндегі заряд:

Q=σ S = $\frac{Е_{0}\ }{4\pi}$ s. (2. 3. 2)

Астарлардағы потенциалдар айырмасын өріс кернеулігі арқылы есептеп таба аламыз. Екі диэлектриктің шекарасындағы потенциалды V` деп белгілейік, сонда

$\frac{V_{1} - V`}{d_{1}}$ = $E_{1}$ , $\frac{V` - V_{2}}{d_{2}}$ = $E_{2}$ ,

бұдан:

$V_{1} - V_{2}$ = $E_{1}$ $d_{1}$ + $E_{2}$ $d_{2}$ = $E_{0}$ $\left( \frac{d_{1}}{\varepsilon_{1}} + \frac{d_{2}}{\varepsilon_{2}}\ \right)$ . (2. 3. 3)

Осы (2. 3. 1) және (2. 3. 3) өрнектерді (2. 3. 1) өрнекке қойсақ, конденсатор сыйымдылығы үшін мынаны табамыз:

С= $\frac{Q}{V_{1} - V_{2}}$ = $\frac{E_{0}S}{4\pi E_{0}\left( \frac{d_{1}}{\varepsilon_{1}} + \frac{d_{2}}{\varepsilon_{2}}\ \right) }$ ,

бұдан

С = $\frac{S}{4\pi\left( \frac{d_{1}}{\varepsilon_{1}} + \frac{d_{2}}{\varepsilon_{2}}\ \right) }$ . (2. 3. 4)

Диэлектрик қабаттарының орналасу ретіне сыйымдылық тәуелсіз екенін байқау оңай. Егер ондағы $d_{2}$ = 0 деп алсақ, бұл формула бір диэлектриктен тұратын конденсатор сыйымдылығының формуласына айналады.

Сфералық конденсатор. Егер конденсатор бірінің ішінде бірі орналасқан өткізгіш сфералардан тұрса, онда ондай конденсаторды сфералық конденсатор дейді(2. 3. 2 - сурет) . Сфералық конденсатор бір - бірімен концентрлі сфералық екі астардан тұрады; олардың радиустарын $R_{1}$ және $R_{2}$ деп белгілейік. Астарлар арасындағы кеңістік диэлектрик тұрақтысы $\varepsilon$ диэлектрикпен толтырылған; астарлар бетінде біркелкі орналасқан зарядтарды +Q және -Q деп, ал астарлардың потенциалдарын сәйкес $V_{1}$ және $V_{2}$ деп белгілейік.

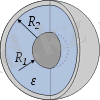
Spherical Capacitor.svg

2. 3. 2- сурет.

Біркелкі зарядталған сфералық беттің тудыратын өрісінің кернеулігі сфераның өз ішінде нөлге тең, ал сфера сыртында шамасы сфера бетіндегі зарядтарға тең, сфераның центріне орналасқан нүктелік зарядтың туғызатын өрісінің кернеулігіндей болады. Осыдан конденсатордың астарлары арасындағы өріс кернеулігі ішкі астардағы зарядтардан жасалады да, ол мынаған тең болады:

E = $\frac{Q}{\varepsilon r^{2}}$

мұнда r - сфералық астардың центрінен саналатын қашықтық.

Бұл r бағыты потенциалдың деңгейлік беттеріне тұрғызылған n нормальдің бағытымен дәл келеді; сондықтан

E = - $\frac{dV}{dr}$ , бұдан dV = - $\frac{Q}{\varepsilon r^{2}}$ dr

мұндағы $\frac{dV}{dr}$ - потенциал градиенті.

Осы өрнекті $R_{1}$ - ден $R_{2}$ - ге дейінгі шекте интегралдай келіп, бір астардан екінші астарға ауысқан кездегі потенциалдың толық өзгерісін табамыз:

$V_{1} - V_{2}$ = - $\int_{R_{1}}^{R_{2}}\frac{Q}{\varepsilon r^{2}}dr$ = $\frac{1}{\varepsilon}$ $\left( \frac{Q}{R_{2}} - \ \frac{Q}{R_{1}} \right)$ .

Осыдан сфералық конденсатордың ізделіп отырған сыйымдылығы мынаған тең:

С = $\frac{Q}{V_{1} - V_{2}}$ = $\frac{Q\varepsilon}{\frac{Q}{R_{1}} - \ \frac{Q}{R_{2}}}$ ,

немесе

C = $\frac{\varepsilon R_{1}R_{2}}{R_{2} - \ R_{1}}$ . (2. 35)

Цилиндрлік конденсатор. Егер ішкі өткізгіщ тұтас металл сым, ал сыртқы өткізгіш тік цилиндр болса, ондай конденсаторды цилиндрлік конденсатор дейді. Цилиндрлік конденсатор ортақ биіктігі l, ал радиустары $R_{1}$ және $R_{2}$ екі коаксиаль қуыс цилиндрден тұрады ( 2. 3. 3- сурет) .

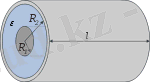
Cylindrical CapacitorII.svg

2. 3. 3- сурет.

Цилиндрлер арасындағы кеңістік диэлектрик тұрақтысы $\varepsilon$ затпен толтырылған. Астарлардағы зарядтар +Q және -Q дейік; астарлардың потенциалдарын $V_{1}$ мен $V_{2}$ арқылы белгілейік.

Астарлар арасындағы өріс кернеулігін тек ішкі цилиндрдегі заряд туғызады да, цилиндр осінен r қашықтықтағы нүктеде ол мынаған тең болады:

E = $\frac{2\eta}{\varepsilon r}$ ,

мұнда η - цилиндрдің бірлік ұзындығына келетін заряд. Потенциалдың dr бойындағы өзгерісі кернеулікпен мына қатыс арқылы байланысты:

dVdr\frac{dV}{dr}= E, осыдан dV = - Edr = -2ηεr\frac{2\eta}{\varepsilon r}dr.

Астарлар арасындағы $V_{2}$ - $V_{1}$ потенциалдар айырмасын осы өрнекті $R_{1}$ және $R_{2}$ шектерінде интегралдаймыз:

$V_{2}$ - $V_{1}$ = - $\int_{R_{1}}^{R_{2}}{\frac{2\eta}{\varepsilon r}\ dr}$ = - $\frac{2\eta}{\varepsilon}$ ln $\frac{R_{2}}{R_{1}}$ .

Сондықтан цилиндрлік конденсатордың сыйымдылығы мынаған тең:

С = $\frac{Q}{V_{1} - V_{2}}$ = $\frac{\varepsilon l}{2\ln\frac{R_{2}}{R_{1}}}$ . (2. 3. 6)

Осылай, цилиндрлік конденсатордың сыйымдылығы оның ұзындығына, әрдайым астарлар арасын толтырып тұратын заттың диэлектрик тұрақтысына тура пропорционал екен; онан соң сыйымдылық тек цилиндрлер радиустарының қатынасына байланысты болады да, осы қатынас кеміген сайын, ол ұлғая түседі.

Сыйымдылығы айнымалы конденсатор. Радиотехникада, көбінесе, құрылысы - суретте көрсетілген, сыйымдылығы айнымалы конденсатор қолданылады. Жарты сақина тәрізді пластиналар ( 2. 3. 4- сурет) біреуін аралата (аттата) өзара қосылған. Пластиналардың тең жартысы қозғалмай тұрады да, екінші жартысы арнайы тұтқаның көмегімен вертикаль осьті айнала алады. Бұраған кезде жылжымалы пластиналар, қозғалмай тұрған пластиналардың ара - арасына азды - көпті кіріп, осылай өзара параллель қосылған бірқатар конденсатор жасайды.

2. 3. 4 - сурет.

Пластиналардан түзілген конденсаторларды жазық конденсаторлар деп те айта аламыз, сондықтан мұндай жеке бір конденсатордың С́ сыйымдылығы мынаған тең деуімізге болады:

С́ = $\frac{\varepsilon S}{4\pi d}$ ,

мұнда $\varepsilon$ - пластиналар арасындағы ортаның диэлектрик тұрақтысы, d - пластиналардың арақашықтығы, S - пластиналардың бір - бірінің ішіне кіріп тұрған бөлігінің ауданы. Егер пластиналар біріне - бірі қатысты $\alpha$ бұрышқа бұрылған болса, онда S - 2. 3. 5, б - суретте штрихталған бөліктің ауданы. Пластиналардың сыртқы радиусын $r_{1}$ , ал ішік радиусын $r_{2}$ арқылы белгілей келіп, мынаны табамыз:

S = $\pi$ ( $r_{1}^{2} - \ r_{2}^{2}$ ) $\frac{\alpha}{2\pi}$ = $\frac{(r_{1}^{2} - \ r_{2}^{2}) \alpha}{2}$ ,

мұндағы бұрыш $\alpha$ радианмен өрнектелген.

Осыдан конденсатордың біреуінің сыйымдылығы мынадай болады:

С́ = $\frac{\varepsilon(r_{1}^{2} - \ r_{2}^{2}) \alpha}{8\pi d}$ .

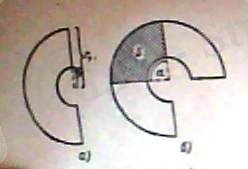
2. 3. 5 - сурет.

Егер тұтас алғанда конденсатор ішіндегі пластиналар арасында n ашық жерлер болса, онда ол әрқайсысының сыйымдылығы С́ параллель қосылған n конденсатордан тұрады.

Ендеше тұтас конденсатордың сыйымдылығы С мынаған тең:

С = nĆ = $\frac{\varepsilon n(r_{1}^{2} - \ r_{2}^{2}) \alpha}{8\pi d}$ , (2. 3. 7)

мұнда $\alpha$ радианмен өрнектелген. Бұл формула $\alpha$ бұрышы кіші болғанда жарамсыз.

Егер $\alpha$ бұрышты градуспен өрнектесек, онда мына қатысқа сүйеніп:

$\alpha$ (радианмен) = $\frac{2\pi}{360}\alpha$ (градуспен)

(2. 3. 7) формуланы мына түрде көшіріп жазамыз:

С = nĆ = $\frac{\varepsilon n(r_{1}^{2} - \ r_{2}^{2}) \alpha}{1440d}$ , (2. 3. 8)

Әдетте мұндай конденсатордың пластиналары арасында ауа болады, ондайда $\varepsilon$ іс жүзінде бірге тең.

Конденсаторларды қосу.

Қажетті электр сыйымдылық алу үшін көптеген жағдайларда конденсаторларды бір - бірімен жалғауға тура келеді. Конденсаторларды тізбектеп қосуға да, параллель қосуға да болады.

Конденсаторларды тізбектей қосу. Сыйымдылықтары $С_{1}$ және $С_{2}$ екі конденсаторды тізбектеп қосу жағдайы 2. 4. 1 - суретте көрсетілген. Сонда 1 - пластинаны +Q зарядпен зарядтаған кезде 2 және 3 - пластиналар тқтас бір өткізгіш болғандықтан, индукция әсерінен, оларда -Q және +Q сәйкес зарядтар пайда болады, ал 4 - пластинада -Q заряд болады.

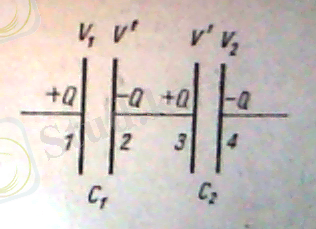
2. 4. 1 - сурет.

Енді 1 - пластинаның потенциалын $V_{1}$ , ал 4 - пластина потенциалын $V_{2}$ деп белгілейік; 2 және 3 - пластиналардың ортақ потенциалын V́- мен белгілейік. Әрбір қос пластина үшін мына қатыстарды жаза аламыз:

$V_{1} - V`$ = $\frac{1}{C_{1}}$ Q, $V_{2} - V`$ = $\frac{1}{C_{2}}$ Q,

мұнда $С_{1}$ және $С_{2}$ - қосылған конденсаторлар сыйымдылығы. Осы теңдіктерді мүшелеп қоссақ, мынадай болады:

$V_{1} - V_{2}$ = $\left( \frac{1}{C_{1}} + \ \frac{1}{C_{2}} \right)$ Q;

екінші жағынан былай жазуға болады:

$V_{1} - V_{2}$ = $\frac{1}{с}$ Q,

мұнда С - күрделі конденсатордың қорытқы сыйымдылығы.

Соңғы екі формуланы салыстыра келіп, мынаны табамыз:

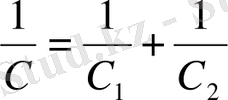(2. 4. 1)

немесе

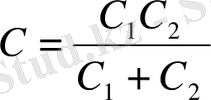(2. 4. 1а)

Сонымен конденсаторларды тізбектеп қосқанда сыйымдылығының кері шамасы қосылған конденсаторлар сыйымдылықтарының кері шамаларының қосындысына тең конденсатор шығады.

Конденсаторларды параллель қосу. Сыйымдылықтары $С_{1}$ және $С_{2}$ конденсаторларды параллель қосқанда (2. 4. 2- сурет) жалғанған пластиналардың потенциалдары бірдей болады. Әр конденсатордың астарларындағы зарядтар әр түрлі болады; оларды $Q_{1}$ және $Q_{2}$ деп белгілейік. Астардағы зарядты потенциалдар айырмасымен және сыйымдылықпен байланыстыратын формуланы әр конденсаторға қолданайық:

$Q_{1}$ = $C_{1}$ ( $V_{1} - V_{2}$ ), $Q_{2}$ = $C_{2}$ ( $V_{1} - V_{2}$ ) .

Осы теңдіктерді мүшелеп қоса келіп, мынаны табамыз:

$Q_{1}$ + $Q_{2}$ = ( $C_{1}$ + $C_{2}$ ) ( $V_{1} - V_{2}$ ) .

Екіншіден былай да жазуға болады:

Q = $Q_{1}$ + $Q_{2}$ = С ( $V_{1} - V_{2}$ ),

мұнда С - екі конденсатордан тұратын системаның сыйымдылығы. Соңғы екі теңдікті салыстыра отырып, мынаны табамыз:

С=С ₁ +С ₂ , (2. 4. 2)

яғни параллель қосылған екі конденсатордың сыйымдылығы олардың сыйымдылықтарының қосындысына тең.

Осы шығарылған нәтижелерді біріктіре қосқан көп конденсаторларға да қолдануға болатыны өзі де түсінікті.

Конденсаторларды системаға келтіріп қосып, іс жүзінде көп қолданады. Арасына парафинделген қағаз не жұқа слюда қабаттары салулы, қорғасын қағаздан істелген жазық конденсатор өте жиі кездеседі. Қорғасын қағаздарды, арада біреуін аттатып (қалдырып), өзара қосады (2. 4. 3 - сурет), сонда өзара қосылған барлық тақ қағаздар, конденсатордың бір астары, ал жұп қағаздар екінші астары болып шығады. Мұндай конденсаторлардың сыйымдылығы жүздеген микрофарада, тіпті одан да артық болады да, өлшемдері сонша шағын болса да, әлденеше жүз вольт кернеуге төтеп бере алады.

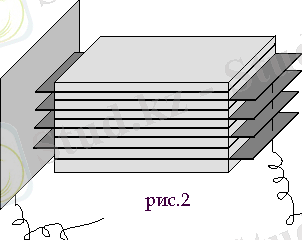
$..\WINDOWS\Application Data\Microsoft\Media Catalog\конден2.bmp$