n-ші ретті айнымалы коэффициентті біртекті сызықтық дифференциалдық теңдеулерді жалпыланған Абель формуласымен шешу


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 52 бет
Таңдаулыға:
Қазақстан Республикасы Білім және ғылым министрлігі
Гуманитарлық-педагогикалық институты
«Физика және математика» кафедрасы
«Қорғауға жіберілді»
Кафедра меңгерушісі
ДИПЛОМДЫҚ ЖҰМЫС
Тақырыбы: n-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулерді жалпыланған
Абель формуласын пайдаланып шешу
050109 - «Математика» мамандығы бойынша
МАЗМҰНЫ
КІРІСПЕ . . . 3
1 ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР КЛАССИФИКАЦИЯСЫ
- Дифференциалдық теңдеулер. Негізгі ұғымдар . . . 4
1. 2 Тұрақты коэффициентті екінші ретті сызықтық дифференцалдық
теңдеулер . . . 12
1. 3 n-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулер . . . 14
2 N-ШІ РЕТТІ, КОЭФФИЦИЕНТТЕРІ АЙНЫМАЛЫ БІРТЕКТІ СЫЗЫҚТЫҚ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІ ШЕШУ ӘДІСТЕРІ. АБЕЛЬ ФОРМУЛАСЫ
2. 1 Дәрежелік қатардың көмегімен дифференциалдық теңдеулерді
интегралдау . . . 28
2. 2 Гипергеометриялық теңдеу . . . 31
2. 3 Бессель теңдеуі . . . 35
2. 4 N-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулерді жалпыланған Абель формуласын пайдаланып шешу
ҚОРЫТЫНДЫ . . . 63
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР . . . 64
КІРІСПЕ
Диплом жұмысының мазмұны n-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулерді жалпыланған Абель формуласын пайдаланып шешуге арналған.
Жұмыс кіріспеден, негізгі екі тараудан және қорытынды мен пайдаланылған әдебиеттер тізімінен тұрады. Бұл тарауларда дифференциалдық теңдеулердің толық классификациясы және дифференциалдық теңдеулерді интегралдаудың әдістері туралы баяндалады.
Механиканың, математикалық физиканың, инженерлік ғылымдардың, сондай-ақ білімнің көптеген салаларын зерттеу дифференциалдық теңдеулерді интегралдауға алып келеді. Ал дифференциалдық теңдеулерді интегралдау түптеп келгенде математикалық анализдің классикалық әрі маңызды сұрақтарының бірі екендігі белгілі.
Болашақ математика пәнінің мұғалімдерін даярлауда пәндер арасындағы сабақтастық пен пәнішілік байланыс өте маңызды. Жоғары оқу орындарында мемлекеттік стандартқа сай математиканың түрлі салаларын оқытуда, оның іс жүзінде қолданылуына айрықша мән беріледі. Айталық, дифференциалдық теңдеулерді шешуді оқып үйренгенде, оның практикалық маңызы ескеріледі және оны шешуде басқа пәндермен байланысы, сабақтастығы қарастырылады.
Дипломдық жұмыста дифференциалдық теңдеулерді қатарлардың көмегімен жуықтап интегралдаудың әдістері қарастырылған. Жұмыстың алғашқы тарауында дифференциалдық теңдеулер туралы негізгі ұғымдар мен теоремалар, негізгі шешу әдістері көрсетіледі. N-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулерге тоқталып, оларды интегралдау әдістерінің математикалық талдау курсының қатарлар теориясымен байланысы туралы айтылады.
Жұмыстың екінші тарауында n-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулер үшін жалпыланған Абель формуласының қолданысы қарастырылған.
Жұмыстың мақсаты: n-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулерді жалпыланған Абель формуласын пайдаланып шешуді көрсету.
Жұмыстың міндеті: математикалық талдаумен пәнішілік байланысты көрсететін мысалдарға тоқталу.
1 ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР КЛАССИФИКАЦИЯСЫ
- Дифференциалдық теңдеулер. Негізгі ұғымдар
Бір немесе бірнеше айнымалылардың ізделінетін функциясын, осы айнымалыларды және функцияның әр түрлі дәрежелі туындыларын байланыстырып тұрған теңдеуді дифференциалдық теңдеу деп атайды.
Егер ізделінетін функция тек бір айнымалыға тәуелді болса, онда дифференциалды теңдеу қарапайым деп, ал егер ол бірнеше айнымалыға тәуелді болса, онда дифференциалды теңдеу дербес туындылы дифференциалдық теңдеу деп аталады.
Біз бұл тарауда тек қарапайым дифференциалдық тендеулерді қарастырамыз. Соңдықтан ендігәрі қарапайым деген сөзді қолданбаймыз.
Дифференциалдық теңдеудің ең жәй түрі - берілген
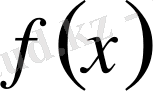 функциясының алғашқы функциясы
функциясының алғашқы функциясы
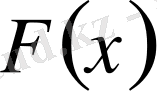 -ты табу есебін береді, өйткені
-ты табу есебін береді, өйткені
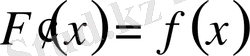 .
.
Дифференциалдық теңдеулерді жалпы түрде былай жазуға болады:
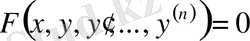 (1)
(1)
Мұнда
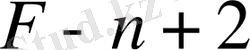 айнымалыға тәуелді функция,
айнымалыға тәуелді функция,
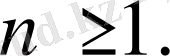
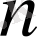 натурал саны (1) теңдеудің дәрежесі деп аталады. Мысалы, функцияның алғашқы функциясын табу есебі - бірінші дәрежелі теңдеуді береді,
натурал саны (1) теңдеудің дәрежесі деп аталады. Мысалы, функцияның алғашқы функциясын табу есебі - бірінші дәрежелі теңдеуді береді,
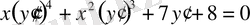
- екінші дәрежелі теңдеу [2] .
Егер
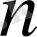 дәрежелі теңдеуді
дәрежелі теңдеуді
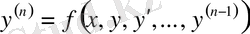
түрінде жазуға болса, онда оны жоғары дәрежелі туындысы бойынша шешілген теңдеу деп атайды. Мұнда
 айнымалыға тәуелді функция.
айнымалыға тәуелді функция.
Егер
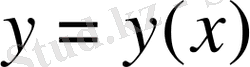 функциясын (1) теңдеуіне апарып қойғанда тепе-теңдік шығатын болса, онда оны (1) теңдеуінің шешімі деп атайды.
функциясын (1) теңдеуіне апарып қойғанда тепе-теңдік шығатын болса, онда оны (1) теңдеуінің шешімі деп атайды.
Мысалы,
у =
cos
2x
функциясы
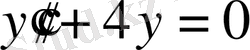 теңдеуінің шешімі балады, өйткені кезкелген
х
үшін
теңдеуінің шешімі балады, өйткені кезкелген
х
үшін
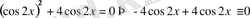
Дифференциалдық теңдеудің шешімін табуды оны интегралдау деп атайды.
Дифференциалдық теңдеу шешімінің графигі дифференциалдық теңдеудің интегралдық қисығы деп аталады [11] .
№19 есеп.
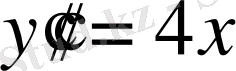 теңдеуінің шешімін табу керек.
теңдеуінің шешімін табу керек.
Шешуі.
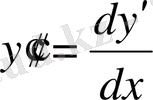 - болғандықтан берілген теңдеуге
- болғандықтан берілген теңдеуге
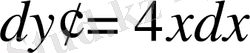 дифференциалдар теңдігі эквивалентті. Соңғы теңдікті ингегралдаймыз:
дифференциалдар теңдігі эквивалентті. Соңғы теңдікті ингегралдаймыз:
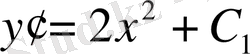
мұндағы
 -кезкелген тұрақты сан.
-кезкелген тұрақты сан.
Осы теңдіктен
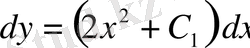 .
.
Олай болса
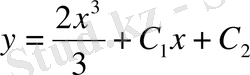 ,
,
мұндағы
 -тұрақты шама.
-тұрақты шама.
 мен
мен
 - тұрақты шамалар. Сондықтан
- тұрақты шамалар. Сондықтан
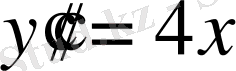 теңдеуінің жазықтықта интегралдық қисықтар үйірі бар. Осы үйірден бір интегралдық қисық бөліп алу үшін жазықтықта осы қисық өтетін нүкте және нүктеден өтердегі бағытын беруіміз керек. Бұл шарттар бастапқы шарттар деп аталады. Мысалы, қарастырылған теңдеуде
теңдеуінің жазықтықта интегралдық қисықтар үйірі бар. Осы үйірден бір интегралдық қисық бөліп алу үшін жазықтықта осы қисық өтетін нүкте және нүктеден өтердегі бағытын беруіміз керек. Бұл шарттар бастапқы шарттар деп аталады. Мысалы, қарастырылған теңдеуде
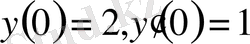 болса, онда
болса, онда
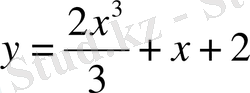
функциясы теңдеудің берілген шарттарды қанағаттандыратын шешімі болады.
(1)
п
дәрежелі дифференциалдық теңдеуін қанағаттаңдыратын,
х
айнымалысына және
 ,
,
 , . . . ,
, . . . ,
 -
п
кезкелген өзара тәуелсіз тұрақты шамаларға тәуелді
-
п
кезкелген өзара тәуелсіз тұрақты шамаларға тәуелді
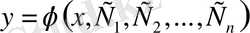 (2)
(2)
функциясын (1) теңдеуінің жалпы шешімі дейді [5] .
Тұрақты шамалардың өзара тәуелсіздігі деп олардың арасындағы ешқандай байланыстың жоқтығын айтамыз.
Жалпы шешімнен
 ,
,
 , . . . ,
, . . . ,
 тұрақты шамаларына нақты мәндер бергенде шығатын функцияны (1) теңдеуінің дербес шешімі дейді.
тұрақты шамаларына нақты мәндер бергенде шығатын функцияны (1) теңдеуінің дербес шешімі дейді.
Мысалы,
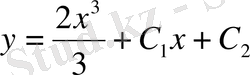 - жалпы шешім, ал
- жалпы шешім, ал
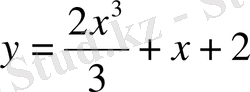 - дербес шешім.
- дербес шешім.
(2) қисықтар үйірін қанағаттаңдыратын дифференциалдық теңдеуді табу үшін оны
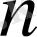 peт дифференциалдау керек.
peт дифференциалдау керек.
№20 есеп.
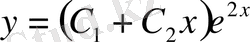 қисықтар үйірінің дифференциалдық теңдеуін табу керек.
қисықтар үйірінің дифференциалдық теңдеуін табу керек.
Шешуі. Берілген функцияны дифференциалдаймыз:
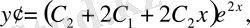
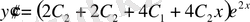
немесе
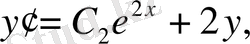
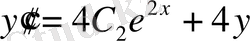 .
.
Осы екі теңдіктен
 -ні жоямыз:
-ні жоямыз:
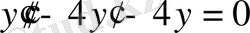 .
.
Дифференциалдық тендеулер экономика, физика, биология, экология сияқты ғалымдардың және тағы басқа салалардың көптеген есептерінен шығады. Бір мысал келтірейік.
№21 есеп.
Статистикалық мағлұматтардан белгілі бір регионда жаңа туған нәрестелермен өлген адамдардың саны бір уақыт бірлігінде барлық тұрғындардың санына пропорционал болатындығы және пропорционалдық коэффициенттердің
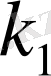 мен
мен
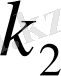 санына теңдігі белгілі болсын. Уақыттың өтуіне байланысты тұрғындар санының өзгеру заңдылығын табу керек.
санына теңдігі белгілі болсын. Уақыттың өтуіне байланысты тұрғындар санының өзгеру заңдылығын табу керек.
Шешуі.
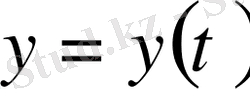 -
-
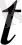 уақытындағы тұрғындардың саны болсын.
уақытындағы тұрғындардың саны болсын.
 мәні
мәні
 уақытындағы тұрғындардың есімі болса, онда
уақытындағы тұрғындардың есімі болса, онда
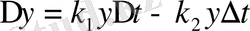 ,
,
яғни ол
 уақыт ішіндегі туғандар саны мен өлгендер санының айырымына тең. Осыдан
уақыт ішіндегі туғандар саны мен өлгендер санының айырымына тең. Осыдан
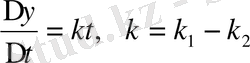 .
.
Осы теңдікте
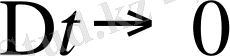 болғанда шекке көшеміз:
болғанда шекке көшеміз:
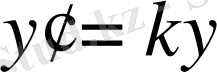 (3)
(3)
(3) теңдеуін шешейік. (3) теңдеуінен
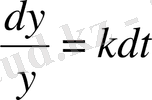 теңдеуі шығады. Олай болса
теңдеуі шығады. Олай болса
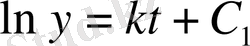 , яғни
, яғни
 , (4)
, (4)
мұндағы С -алғашқы шарттар бойынша анықталатын тұрақты шама. Алғашқы шарттар ретінде тұрғындардың бастапқы санын алуға болады.
- Тұрақты коэффициентті екінші ретті сызықтық
дифференцалдық теңдеулер
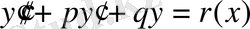 (5)
(5)
түріндегі теңдеу
р
мен
q
тұрақты шамалар болғанда тұрақты коэффициент екінші ретті сызықтық дифференциалдық теңдеу деп аталады. Мұндағы
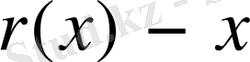 -ке тәуелді функция.
-ке тәуелді функция.
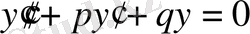 (6)
(6)
теңдеуі біртекті, ал (5)
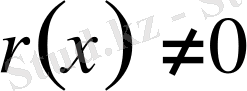 болғанда біртексіз теңдеу деп аталады [12] .
болғанда біртексіз теңдеу деп аталады [12] .
(5) теңдеуінің
 теңдіктерін қанағаттандыратын тек бір ғана шешімі бар.
теңдіктерін қанағаттандыратын тек бір ғана шешімі бар.
Егер
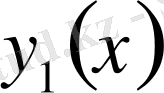 пен
пен
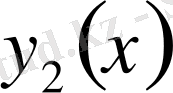 функцияларының сызықтық өрнегі
функцияларының сызықтық өрнегі
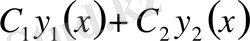 (мұндағы
(мұндағы
 мен
мен
 тұрақты шамалар) нөлге тең болу үшін
тұрақты шамалар) нөлге тең болу үшін
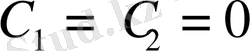 теңдіктері орындалса, онда осы функциялар өзара сызықтық тәуелсіз функциялар деп аталады, ал егер сызықтық өрнек
теңдіктері орындалса, онда осы функциялар өзара сызықтық тәуелсіз функциялар деп аталады, ал егер сызықтық өрнек
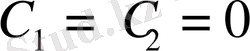 теңдіктері орындалмаған жағдайда да нөлге тең болса, онда
теңдіктері орындалмаған жағдайда да нөлге тең болса, онда
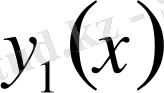 пен
пен
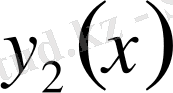 өзара сызықтық тәуелді функциялар деп аталады.
өзара сызықтық тәуелді функциялар деп аталады.
№22 есеп. Төмендегі функциялардың өзара сызықтық тәуелсіз екендігін көрсету керек:
1)
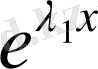 және
және
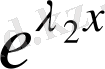 ,
,
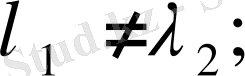
2)
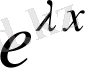 және
және
 ;
;
3)
 және
және
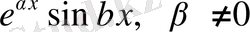 .
.
Шешуі.
1) Егер
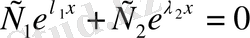 болса, онда
болса, онда
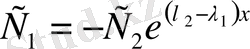 . Олай болса
. Олай болса
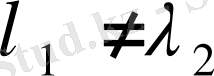 болғандықтан
болғандықтан
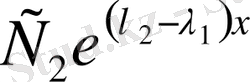 тұрақты шама болу үшін
тұрақты шама болу үшін
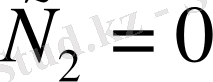 болу керек. Осыдан
болу керек. Осыдан
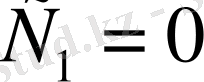 екендігі шығады;
екендігі шығады;
2)
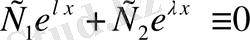 болу үшін
болу үшін
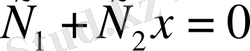 болу керек. Соңғы теңдіктен
болу керек. Соңғы теңдіктен
 болғанда
болғанда
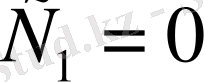 теңдігі шығады. Олай болса
теңдігі шығады. Олай болса
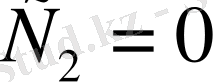 ;
;
3)
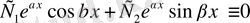 болсын. Онда
болсын. Онда
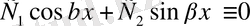
болады. Осы теңдіктен
 болғанда
болғанда
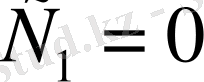 шығады. Соңдықтан
шығады. Соңдықтан
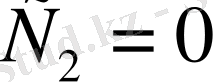 .
.
Егер
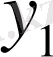 мен
мен
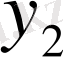 функциялары (6) теңдеуінің шешімдері болса, онда олардың сызықтық өрнегі
функциялары (6) теңдеуінің шешімдері болса, онда олардың сызықтық өрнегі
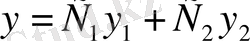 (7)
(7)
функциясы да (6) теңдеуінің шешімі болады.
Бұл тұжырымды (7) функциясын (6) -ге қою арқылы дәделдейміз:
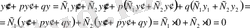
Осы тұжырымды пайдаланып төмендегі теорема дәлелденеді.
Теорема 7.
Егер
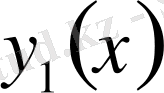 пен
пен
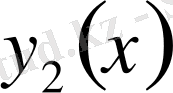 өзара сызықты тәуелсіз (6) теңдеуінің шешімдері болатын болca, онда (6) теңдеудің жалпы шешімі (7) формуласы бойынша табылады [13] .
өзара сызықты тәуелсіз (6) теңдеуінің шешімдері болатын болca, онда (6) теңдеудің жалпы шешімі (7) формуласы бойынша табылады [13] .
Сонымен (6) теңдеуінің жалпы шешімін табу үшін оның өзара сызықтық тәуелсіз екі шешімін білу керек.
(6) теңдеуінің шешімін
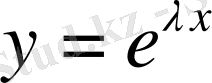 (8)
(8)
түрінде іздейміз. Мұндағы
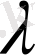 -нақты сан.
-нақты сан.
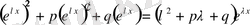
болғандықтан (8) функциясы (6) теңдеудің шешімі болу үшін
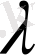 саны
саны
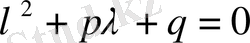 (9)
(9)
теңдеуінің түбірі болу керек.
(9) теңдеуі (6) теңдеуінің сипаттаушы теңдеуі деп аталады. (6) теңдеудің шешімдерінің бар болуы сипаттаушы теңдеудің түбірлерінің бар болуына байланысты. (6) теңдеуінің шешімдері үшін темендегі тұжырымдардың растығын дәлелдеуге болады.
Теорема 8.
а) Егер сипаттаушы теңдеудің екі нақты
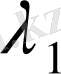 және
және
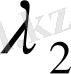 түбірлері бар болса, онда (6) теңдеудің жалпы шешімі
түбірлері бар болса, онда (6) теңдеудің жалпы шешімі
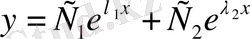 (10)
(10)
түрінде беріледі. Мұндағы
 мен
мен
 кезкелген тұрақты шамалар;
кезкелген тұрақты шамалар;
ә) егер сипаттаушы теңдеудің бір еселі
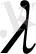 түбірі бар болса, онда (6) теңдеудің жалпы шешімі
түбірі бар болса, онда (6) теңдеудің жалпы шешімі
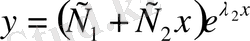 (11)
(11)
түрінде беріледі. Мұндағы
 мен
мен
 кезкелген тұрақта шамалар;
кезкелген тұрақта шамалар;
б) егер сипаттаушы теңдеудің нақты түбірлері болмаса, онда (6) теңдеудің жалпы шешімі
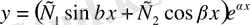 (12)
(12)
түрінде беріледі. Мұндағы
 мен
мен
 кезкелген тұрақты шамалар, ал
кезкелген тұрақты шамалар, ал
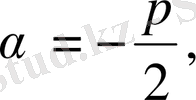
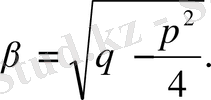
№23 есеп.
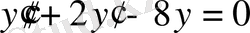 теңдеуінің жалпы шешімін табу керек.
теңдеуінің жалпы шешімін табу керек.
Шешуі.
Сипаттаушы теңдеуді жазамыз:
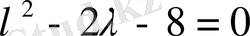 . Мұның түбірлері
. Мұның түбірлері
 және
және
 . Сондықтан (10) теңдеу бойынша
. Сондықтан (10) теңдеу бойынша
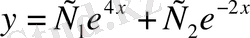
функциясы іздеп отырған жалпы шешім болады.
№24 есеп.
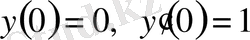 алғашқы шарттарын қанагаттандыратын
алғашқы шарттарын қанагаттандыратын
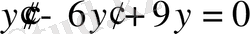 теңдеуінің шешімін табу керек.
теңдеуінің шешімін табу керек.
Шешуі.
Алдымен берілген теңдеудің жалпы шешімін табамыз. Ол үшін сипаттаушы теңдеуді құрамыз:
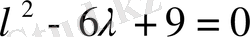 . Мұның еселік түбірі бар:
. Мұның еселік түбірі бар:
 . Сондықтан (11) формуласы бойынша
. Сондықтан (11) формуласы бойынша
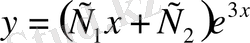 функциясы берілген теңдеудің жалпы шешімі болады. Енді осы жалпы шешімнен алғашқы шарттарды қанағаттандыратын дербес шешімді бөліп аламыз:
функциясы берілген теңдеудің жалпы шешімі болады. Енді осы жалпы шешімнен алғашқы шарттарды қанағаттандыратын дербес шешімді бөліп аламыз:
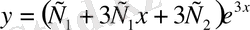
болғандақтан
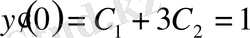 ,
,
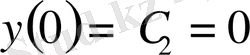 .
.
Сонымен
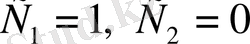 . Олай болса
. Олай болса
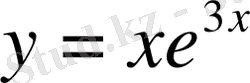 функциясы іздеп отарған шешім болады.
функциясы іздеп отарған шешім болады.
№25 есеп.
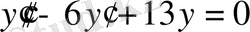 теңдеуінің жалпы шешімін табу керек.
теңдеуінің жалпы шешімін табу керек.
Шешуі. Сипаттаушы теңдеуді құрамыз:
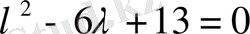 .
.
Бұл теңдеудің нақты түбірлері жоқ. Сондықтан (12) формуласы бойынша
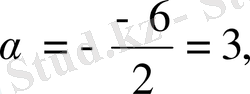
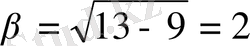 болғандықтан
болғандықтан
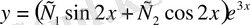
функциясы берілген теңдеудің жалпы шешуі болады.
Енді (5) теңдеуінің жалпы шешімін табуға көшейік. Оны тұрақтыны вариациялау әдісімен табуға болады. Ол үшін алдымен біртекті (6) теңдеуінің жалпы шешімін табады:
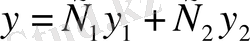 .
.
Содан соң (5) теңдеудің жалпы шешімі
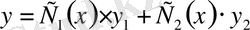
түрінде ізделінеді. Мұндағы
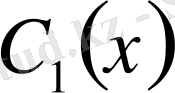 пен
пен
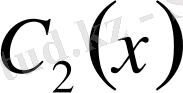 әзірше белгісіз функциялар. Оларды
әзірше белгісіз функциялар. Оларды
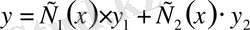
функциясы (5) теңдеуді қанағаттандыратындай етіп таңдап алады. Сондықтан олар
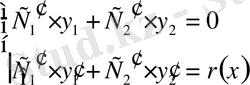 (13)
(13)
теңдеулер жүйесінің шешімдері ретінде табылады. Мұны біз мысалмен керсетелік.
№26 есеп.
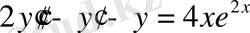 теңдеуінің жалпы шешімін табу керек.
теңдеуінің жалпы шешімін табу керек.
Шешуі. Теңдеуді (5) түріне келтіреміз:
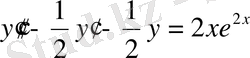 .
.
Сипаттаушы теңдеуді құрамыз:
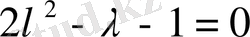 .
.
Мұның шешімдері
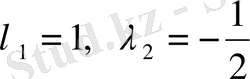 . Сондықтан
. Сондықтан
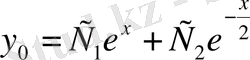
біртекті теңдеудің жалпы шешімі. Енді біртексіз теңдеудің жалпы шешімін
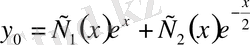
түрінде іздейміз. Ол үшін (13) жүйесін құрамыз:
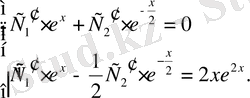
Осыдан
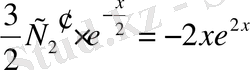
немесе
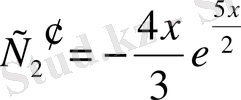 .
.
Олай болса
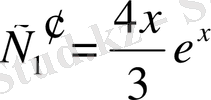 .
.
Сондықтан
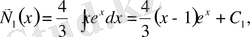
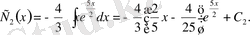
Сонымен
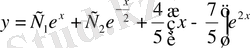
функциясы ізделіп отырған жалпы шешім болады. Табылған шешімнің құрамына назар аударатын болсақ, онда алғашқы екі мүшенің қосындысы
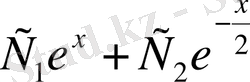
- біртекті теңдеудің жалпы шешімі, ал
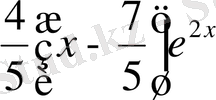
- біртексіз теңдеудің дербес шешімі екенін көреміз.
Осындай құбылыс кезкелген сызықтық біртекті емес теңдеу үшін байқалады, яғни мынандай тұжырым дұрыс болады:
Теорема 9. Біртексіз сызықты дифференциалдық теңдеудің жалпы шешімі осы тендеудің бір дербес шешімі мен сәйкес біртекті сызықты дифференциалдық теңдеудің жалпы шешімдерінің қосындысынан тұрады /3/.
1. 3 n-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулер
1. 3. 1 Жоғары ретті дифференциалдық теңдеулер
Анықтама.
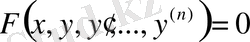 (17)
(17)
түріндегі теңдеу n -ретті дифференциалдық теңдеу деп аталады.
Егер (17) -ден n -і туынды табылатын болса, онда
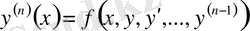 (18)
(18)
теңдеуі ең жоғарғы туындысы арқылы шешілген n -ретті дифферен-циалдық теңдеу деп аталады.
Коши есебі:
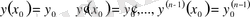 (19)
(19)
бастапқы шарттарды қанағаттандыратын (18) дифференциалдық теңдеудің шешімін табалық.
Теорема (Коши есебі шешімінің бар және оның жалғыз болуы туралы) .
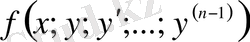 функциясы
функциясы
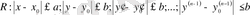
облысында мына екі шартты қанағаттандырсын делік:
1)
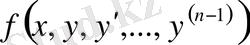 функциясы өздерінің аргументтері бойынша үзіліссіз және шенелген:
функциясы өздерінің аргументтері бойынша үзіліссіз және шенелген:
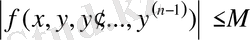 ;
;
2) функция үшін
 айнымалылары бойынша
айнымалылары бойынша
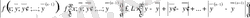
Липшиц шарты орындалады (Липшиц шарты функциядан
 айнымалылары бойынша алынған үзіліссіз дербес туындылары бар болғанда ғана орындалады), онда анықталған, өзінің
n
-і туындыларымен қоса үзіліссіз және (19) бастапқы шарттарды қанағаттандыратын жалғыз
айнымалылары бойынша алынған үзіліссіз дербес туындылары бар болғанда ғана орындалады), онда анықталған, өзінің
n
-і туындыларымен қоса үзіліссіз және (19) бастапқы шарттарды қанағаттандыратын жалғыз
 шешімі бар болады.
шешімі бар болады.
Бұл теореманы жеңілдеу тұжырымдауға болады.
Егер (18) дифференциалдық теңдеудің оң бөлігі үзіліссіз, шенелген және
 бойынша үзіліссіз дербес туындылары болса, онда Коши есебінің жалғыз шешімі бар болады.
бойынша үзіліссіз дербес туындылары болса, онда Коши есебінің жалғыз шешімі бар болады.
Анықтамалар.
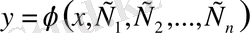
функциясы (18) дифференциалдық теңдеудің жалпы шешімі деп аталады, егер ол:
1)
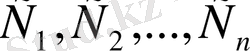 -дың кез келген мәндерінде (18) дифференциалдық теңдеуді қанағаттандырады;
-дың кез келген мәндерінде (18) дифференциалдық теңдеуді қанағаттандырады;
2) берілген (19) бастапқы шарттар бойынша
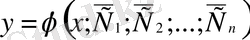 функциясы (19) бастапқы шарттарды қанағаттандыратын мынадай
функциясы (19) бастапқы шарттарды қанағаттандыратын мынадай
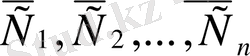 -і табуға болады.
-і табуға болады.
Егер жалпы шешімінде
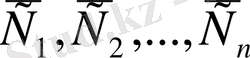 -ң нақты мәндері алынатын болса, онда функция дифференциалдық теңдеудің дербес шешімі деп аталады.
-ң нақты мәндері алынатын болса, онда функция дифференциалдық теңдеудің дербес шешімі деп аталады.
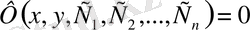
түріндегі қатысы, мұндағы
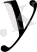 айқын берілмеген, (18) дифференциалдық теңдеудің жалпы интегралы деп аталады
айқын берілмеген, (18) дифференциалдық теңдеудің жалпы интегралы деп аталады
(18) теңдеуді интегралдау үшін бастапқы шарттарды қанағаттандыратын жалпы шешімін немесе дербес шешімін табу қажет.
1. 3. 2 Жоғары ретті дифференциалдық теңдеулерді интегралдаудың тәсілдері
I-класс . Тәуелсіз айнымалы және жоғарғы туындысы бар теңдеулер.
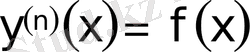
түріндегі теңдеуді қарастырамыз.
Екі бөлігін де
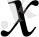 бойынша интегралдаймыз:
бойынша интегралдаймыз:
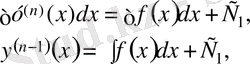
тағы да интегралдаймыз:
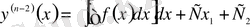 .
.
Осы тәсілмен n рет интегралдаймыз, сонда
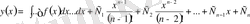 .
.
I-кластағы n -ретті ДТ тізбектей n рет интегралдау тәсілімен шешіледі.
Мысал.
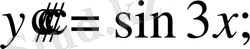 теңдеуін шешелік.
теңдеуін шешелік.
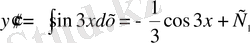 ;
;
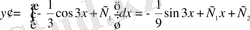 ;
;
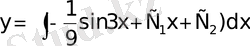
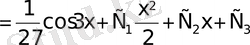 .
.
II-класс. у функциясы және оның (k-1) -і ретіне дейінгі туындылары жоқ теңдеулер.
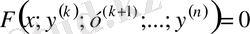
түріндегі ДТ қарастырамыз.
Жаңа айнымалы енгіземіз:
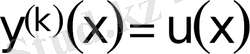 , (20)
, (20)
сонда
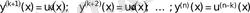 .
.
u(х) функциясы мен оның алынған туындыларын қарастырылатын теңдеуге қоямыз:
 .
.
Сонымен,
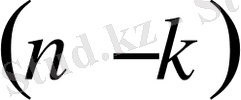 - ретті теңдеу алынды, яғни ДТ-ң реті төмендетілді. Жаңа ДТ-ң шешімі
- ретті теңдеу алынды, яғни ДТ-ң реті төмендетілді. Жаңа ДТ-ң шешімі
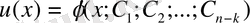
функциясы болсын делік. Мұны (20) теңдеуге қоямыз:
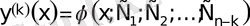
- k ретті дифференциалдық теңдеу аламыз, ал бұл k рет дифферен-циалдау арқылы шешіледі (1-класс) .
Мысалдар
.
1.
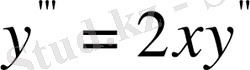 үшінші ретті ДТ шешелік.
үшінші ретті ДТ шешелік.
 ауыстыруын алайық,
ауыстыруын алайық,
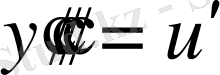 .
Бұларды теңдеуге қою арқылы
.
Бұларды теңдеуге қою арқылы
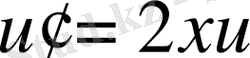 бірінші ретті ДТ-і аламыз. Айнымалыларын ажыратамыз:
бірінші ретті ДТ-і аламыз. Айнымалыларын ажыратамыз:
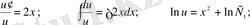
 ;
;
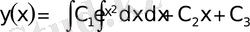 .
.
Бұл теңдеу квадратурада шешіледі.
2.
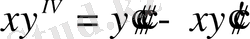 ;
;
 ;
;
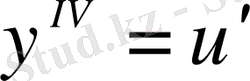 ;
;
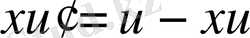 ;
;
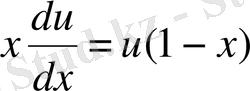 ;
;
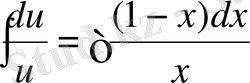 ;
;
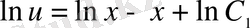 ;
;
 ;
;

бұл теңдеуді бөліктеп үш рет интегралдау арқылы шешу керек (1-класс)
III-класс . Тәуелсіз айнымалы х- і жоқ теңдеулер.
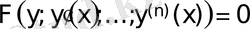
түріндегі теңдеуін қарастырамыз.
Тәуелсіз жаңа айнымалы үшін у- ті аламыз және ауыстыру орындаймыз:
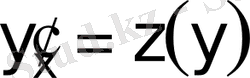 .
.
Екінші, үшінші және т. б. туындыларын алу үшін осы жаңа функциядан күрделі функция есебінде туынды табамыз:
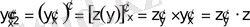 ;
;
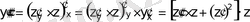
және т. б.
Табылған туындыларды теңдеуге қойып, реті бірге кеміген ДТ аламыз:
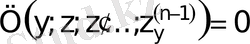 .
.
Шешімі мына түрде табылды делік:
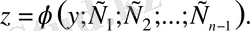
Енді ауыстыруға қайта оралып айнымалылары ажыратылған бірінші ретті ДТ аламыз:
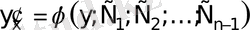 .
.
Мысал.
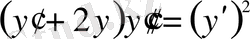 ДТ шешелік. Мұнда тәуелсіз айнымалы
х
жоқ.
ДТ шешелік. Мұнда тәуелсіз айнымалы
х
жоқ.
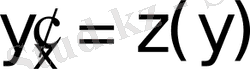 ауыстыруын орындаймыз.
ауыстыруын орындаймыз.
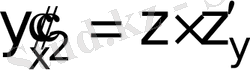 ;
;
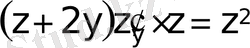 - бұл біртекті теңдеу.
- бұл біртекті теңдеу.
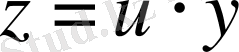 - ауыстыруын аламыз,
- ауыстыруын аламыз,
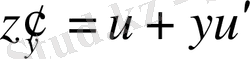 . Теңдеуге қоямыз:
. Теңдеуге қоямыз:
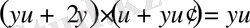 .
у-
і қысқартамыз:
.
у-
і қысқартамыз:
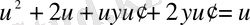 .
.
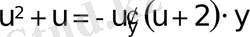 ;
;
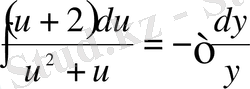 ;
;
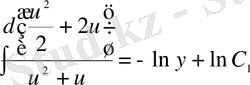 ;
;
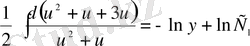 - біртекті теңдеудің шешімі
- біртекті теңдеудің шешімі
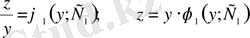 немесе
немесе
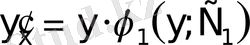 ,
,
ал бұл айнымалысы ажыратылған ДТ.
IV класс. Сол бөлігі толық туынды болып келген теңдеулер.
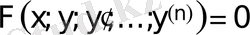
теңдеуін қарастырамыз және
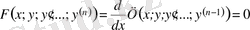
болсын делік. Жаңа дифференциалдық теңдеудің екі бөлігін де интегралдаймыз, сонда
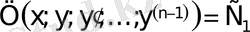 .
.
ДТ реті бірге төмендеді.
Мысалдар.
1.
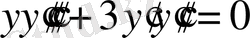 . Бұл III-кластың теңдеуі. IV-кластың тәсілімен шешіп көрелік.
. Бұл III-кластың теңдеуі. IV-кластың тәсілімен шешіп көрелік.
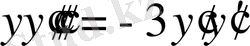 , екі бөлігін де
, екі бөлігін де
 -ке бөлеміз:
-ке бөлеміз:
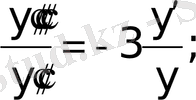 енді интегралдаймыз:
енді интегралдаймыз:
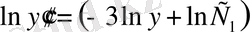 ;
;
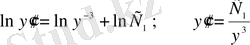 - теңдеудің
х-
і жоқ.
- теңдеудің
х-
і жоқ.
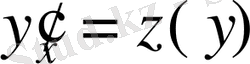 ;
;
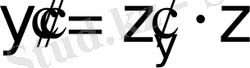 ;
;
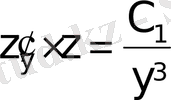 ;
;
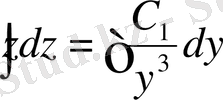 ;
;
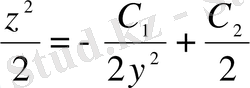 ;
;
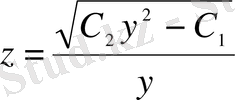 ;
;
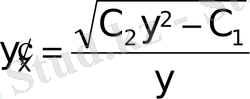 ;
;
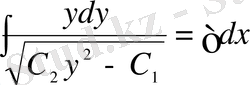 ;
;
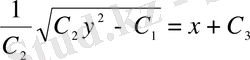
- бұл үшінші ретті ДТ жалпы интегралы, сондықтан оның үш еркін тұрақтысы бар.
2.
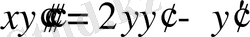 ;
;
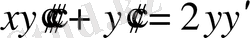 ;
;
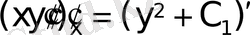 ;
;
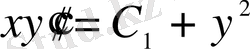 - бұл ДТ реті бірге төмендеді.
- бұл ДТ реті бірге төмендеді.
3.
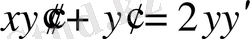 .
.
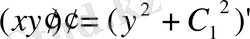 ;
;
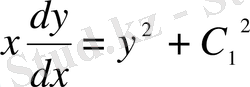 ;
;
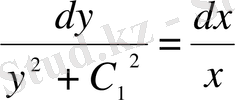 ;
;
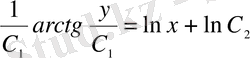 ;
;
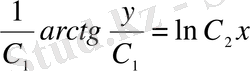 - бұл ДТ жалпы интегралы.
- бұл ДТ жалпы интегралы.
Сызықтық дифференциалдық теңдеулер
Анықтама.
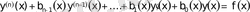 (21)
(21)
түріндегі дифференциалдық теңдеулер n -ретті сызықтық дифферен-циалдық теңдеулер (СДТ) деп аталады.
Бұл теңдеуде
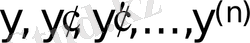 -лер бірінші дәрежелі.
-лер бірінші дәрежелі.
2 N-ШІ РЕТТІ, КОЭФФИЦИЕНТТЕРІ АЙНЫМАЛЫ БІРТЕКТІ СЫЗЫҚТЫҚ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІ ШЕШУ ӘДІСТЕРІ. АБЕЛЬ ФОРМУЛАСЫ
2. 1. 1 Абель Нильс Хенрик
Абель Нильс Хенрик (Niels Henrik Abel, 1802-1829) - Норвегияның атақты математигі, осы заман алгебрасының дамуындағы көшбасшысы. 1802 ж. 5-тамыз күні Финнейде шала сопы-пастор сурен Георт Абелдің семьясында дүниеге келген, 1829 ж. 6-сәуір күні Фолуланда қайтыс болған.
13 жасында Ослода діни мектепке түскен, математика мүғалімі Бернт Микель Хольмобое оның талантын байқап, оған жетекшілік еткен. Жас шағынан бастап Абель кейбір математикалық мәселелерге ой жүгірте бастайды. 1821 жылы бірнеше профессордың көмегімен Осло университетіне түседі. Ол университетте өздігінен оқыған, сонымен бірге көп уақытын зерттеуге жұмсаған. 1824 жылы, Абель 5-дәрежелі алгебралық теңдеудің шешуін әдеттегі түбір табу жолымен табуға болмайтынын дәлелдеу барысында, топтарға (Абел тобына) алмастыруға болады деген тұжырымды енгізеді. Мақаласы түсінікті болу үшін француз тілінде жарялайды және оны С. Ф. Гауссқа жіберіп береді. Бірақ шет ел математиктері ешқандай көмек көрсетпейді. 1825 жылы ол Берлинге барып, сол жерде А. Л. Креллемен (August Leopold Crelle 1780-1855) танысып дос болады.
Абель Нильс Хенрик-Норвегияның атақты математигі
2. 1. 2
2. 2
2. 3
2. 4
1 САНДЫҚ ЖӘНЕ ФУНКЦИОНАЛДЫҚ ҚАТАРЛАР
1. 1 Негізгі ұғымдар мен теоремалар
Айталық, шексіз сандық тізбек берілсін.
 (1)
(1)
Мына
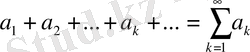 (2)
(2)
шексіз аналитикалық түрлендіру (1) сандық тізбектің қосындысын көрсетеді және сандық қатар деп аталады. Ал
 сандары қатардың мүшелері деп аталады. (2) қатар берілді деп санаймыз. Егер осы қатардың мүшелерінің берілу заңы белгілі болса, бұл жағдайда мынадай варианттар мүмкін:
сандары қатардың мүшелері деп аталады. (2) қатар берілді деп санаймыз. Егер осы қатардың мүшелерінің берілу заңы белгілі болса, бұл жағдайда мынадай варианттар мүмкін:
- қатардың алғашқы бірнеше мүшесі белгілі, осыдан барып қатардың жалпы мүшесін табуға болады. Мысалы,
1.
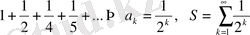 .
.
2.
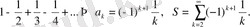
3.
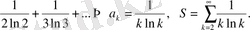
- қатардың жалпы мүшесі
 берілген, қатарды жазу керек. Мысалы,
берілген, қатарды жазу керек. Мысалы,
1.
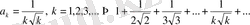
2.
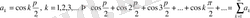
түрінде жазылған сиволикалық жазу осы қатардың қосындысы деп аталады. Ал бұны түсіндіру үшін қатардың n мүшесінен дербес қосынды деп аталатын қосындылар құрайық:
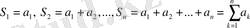
Нәтижесінде жаңа сандық тізбек аламыз:
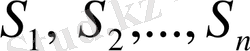 . (3)
. (3)
Егер
 ұмтылғанда (3) тізбектің шегі болса,
ұмтылғанда (3) тізбектің шегі болса,
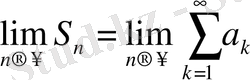 ,
,
онда (2) шексіз сандар қатар жинақты және қатардың қосындысы бар болады.
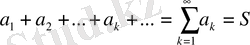 (4)
(4)
Егер
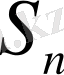 -нің шегі жоқ болса, онда (2) қатар жинақсыз және қосындысы жоқ дейміз.
-нің шегі жоқ болса, онда (2) қатар жинақсыз және қосындысы жоқ дейміз.
Егер
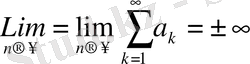
болса, онда (2) қатар жинақсыз деп аталады. Егер (4) қатар жинақты болса, онда жеткілікті үлкен
n
нөмірлі
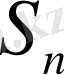 дербес қосынды қатардың
дербес қосынды қатардың
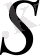 қосындысына жуық түрде тең болады.
қосындысына жуық түрде тең болады.
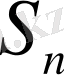 дербес қосынды мен қатардың қосындысы арасындағы
дербес қосынды мен қатардың қосындысы арасындағы
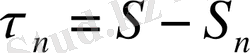 (5)
(5)
жуақтау қателігі (2) қатардың қалдығы деп аталады.
(5) қалдық
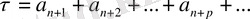
(2) қатардың алғашқы n мүшесін алып тастағаннан шығады [1], [2] .
Қатардың қалдығы туралы теорема
Егер (2) қатар беріліп, (5) қатар оның кез келген қалдығы болса, (2) қатардың жинақталуынан (5) қалдықтың дажнақталуы және керісінше, (5) қатардың жинақталуынан (2) қатардың жинақталатындығы шығады.
Қатардың жинақтылығының қажетті шарты
Теорема 1.
Егер кезкелген сандық қатар жинақты болса, онда оның жалпы мүшесінің шегі бар және нольге тең:
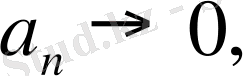 егер
егер
 .
.
Дәлелдеу
: Айталық, бізге
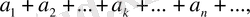 жинақты қатар берілсін, яғни
жинақты қатар берілсін, яғни
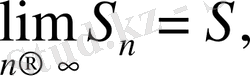
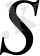 -қатардың қосындысы. Онда
-қатардың қосындысы. Онда
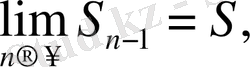 үшін де орынды. Ал,
үшін де орынды. Ал,
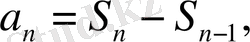
бұдан
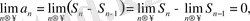
дәлелдеу керегі де осы.
Берілген шарт қажетті, бірақ жеткілікті емес, яғни ол орныдалады, бірақ бұл қатардың жинақты екенін көрсетпейді [2] .
№1 есеп.
а)
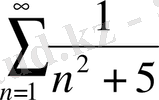 орындалады,
орындалады,
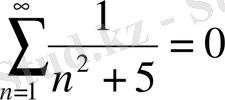
б)
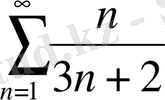 орындалмайды,
орындалмайды,
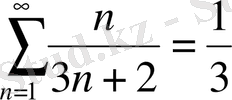 .
.
в)
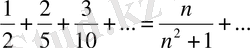 орындалады,
орындалады,
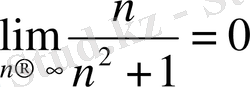 .
.
№2 есеп. Қатардың жинақтылығын зерттеу керек.
а)
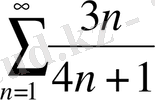 ;
;
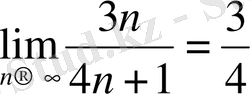 , қатар жинақсыз.
, қатар жинақсыз.
б)
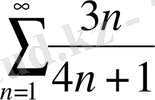 қажетті шартын тексереміз.
қажетті шартын тексереміз.
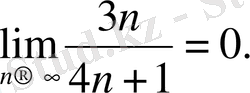 тізбек жазамыз:
тізбек жазамыз:
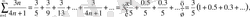
тізбек монотонды кемиді, ал
 , яғни қатар жинақсыз [3] .
, яғни қатар жинақсыз [3] .
Қатарларға амалдар қолдану
- Жинақты қатарды тұрақтыссанына көбейткенде жинақты қатар шығады. жинақты, яғни
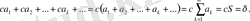
- Жинақты бірнеше қатардың қосындысы да жинақты.
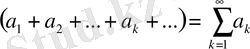
және
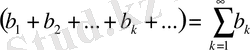
қатарлары жинақты болсын. Онда
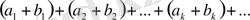
қатары да жинақты. Бұл крісінше болса, үнемі орындала бермейді.
Мысалы,
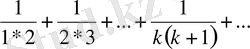 жинақты қатар. Бірақ бұл қатар екі жинақсыз қатардың қосындысы болып табылады.
жинақты қатар. Бірақ бұл қатар екі жинақсыз қатардың қосындысы болып табылады.
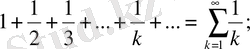
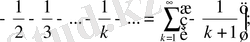
Мүшелері оң қатарлар
Мына түрде
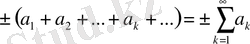 ,
,
берілген қатар біртаңбалы деп аталады. «Минус» таңбалы қатардың жинақтылығына әсер етпейтіндіктен, бұнда тек қана мүшелері оң қатармен ғана шектелеміз.
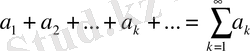 , (6)
, (6)
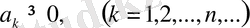 .
.
(6) қатардың дербес қосындылары
 монотонды өспелі сандық тізбекті береді. Бізге белгілі, бұндай тізбек шектелген немесе шексіз өспелі болады. Бұдан (6) қатар шексіздікте жинақты не жинақсыз болуы мүмкін [4] .
монотонды өспелі сандық тізбекті береді. Бізге белгілі, бұндай тізбек шектелген немесе шексіз өспелі болады. Бұдан (6) қатар шексіздікте жинақты не жинақсыз болуы мүмкін [4] .
Қатарларды салыстыру белгісі
Теорема 2.
Мүшелері оң
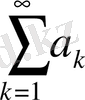 (А) мен
(А) мен
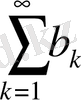 (В) қатарларының мүшелері (белгілі бір
(В) қатарларының мүшелері (белгілі бір
 -нен бастап)
-нен бастап)
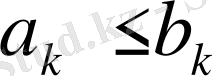 шартын қанағаттандырса, біріншіден, (А) қатардың жинақталмауынан (В) қатарының жинақталмайтындығы шығады; екіншіден, (В) қатардың жинақталуынан (А) қатарының жинақталатындығы шығады.
шартын қанағаттандырса, біріншіден, (А) қатардың жинақталмауынан (В) қатарының жинақталмайтындығы шығады; екіншіден, (В) қатардың жинақталуынан (А) қатарының жинақталатындығы шығады.
Салыстыру белгісін пайдаланып, қатардың жинақтылығын тексеру керек.
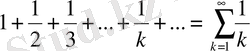 (7)
(7)
бұл қатар гормоникалық қатар деп аталады. Егер кезкелген қатар тұрған үш мүшесін алсақ,
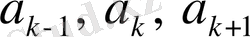 онда
онда
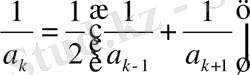 шартн қанағаттандыратынын көреміз. (7) гормоникалық қатар жинақтылықтың қажетті шартын қанағаттандырады.
шартн қанағаттандыратынын көреміз. (7) гормоникалық қатар жинақтылықтың қажетті шартын қанағаттандырады.
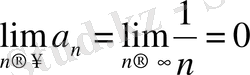 . Бірақ бұл қатардың
. Бірақ бұл қатардың
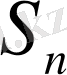 дербес қосындысын
дербес қосындысын
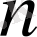 өскен сайын шексіз өсетінін көрсетуге болады. Бұл үшін қатардың екінші мүшесінен бастап қатар мүшелерін біріктіреміз.
өскен сайын шексіз өсетінін көрсетуге болады. Бұл үшін қатардың екінші мүшесінен бастап қатар мүшелерін біріктіреміз.
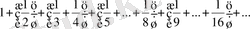
Егер группадаға әрбір қосылғышты соңғысымен ауыстырсақ,
 (8)
(8)
(8) қатардың мүшелері (7) қатардың сәйкес мүшелерінен асып кетпейді. Бірақ (8) қатардың әрбір дербес қосындысы
 -да
-да
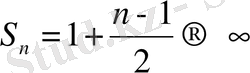 , яғни (8) қатар жинақсыз. Бұдан салыстыру белгісі бойынша (7) армоникалық қатар да жинақсыз болады.
, яғни (8) қатар жинақсыз. Бұдан салыстыру белгісі бойынша (7) армоникалық қатар да жинақсыз болады.
Даламбер белгісі
Егер мүшелері оң қатар үшін
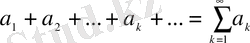 ,
,
шек бар болса,
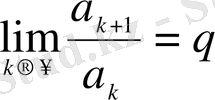 ,
,
1.
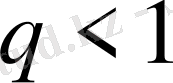 болғанда қатар жинақты.
болғанда қатар жинақты.
2.
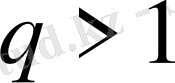 болғанда қатар жинақсыз.
болғанда қатар жинақсыз.
Дәлелдеу
:
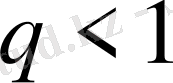 болсын. Онда қандай да бір
болсын. Онда қандай да бір
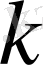 -дан бастап, мына шарт
-дан бастап, мына шарт
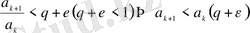 ,
,
орынды.
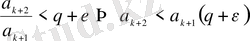 (9)
(9)
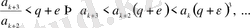
Негізгі қатарды жазамыз,
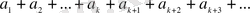 (10)
(10)
және көмекші қатарды жазамыз:
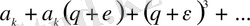 (11)
(11)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz