«Бөлшек сандары бір санау жүйесінен екінші санау жүйесіне ауыстыру»

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

Қазақстан Республикасы білім және ғылым министрлігі

Нұр-Мубарак Египет ислам мәдениеті университеті

РЕФЕРАТ

Тақырыбы :

«бөлшек сандары бір санау жүйесінен екінші санау жүйесіне ауыстыру»

Орындаған: Бексултанов Н.

Тексерген: Самат Сайлаубайулы

2013 жыл

Жоспар :

Бүтін ондық санды басқа позициялық санау жүйесіне ауыстыру.
Дұрыс ондық бөлшекті басқа позициялық санау жүйесіне ауыстыру.
Бүтін сандарды бір санау жүйесінен екінші санау жүйесіне

түрлендірудің жалпы тәртіптері.

Бүтін ондық санды басқа позициялық санау жүйесіне ауыстыру

Берілген бүтін N ондық санын негізі q болып келген санау жүйесіне ауыстыру үшін сол N- ді қалдығын таба отырып ("бүтін бөлінді" алу жолымен) q- ге ондық жүйеде бөлу керек. Сонан соң шыққан бүтін бөліндіні қайтадан қалдығын таба отырып q -ге бөлу қажет, т. с. ж., бөлу процесі бөлінді 0 -ге тең болған кезде тоқтатылады. N санының жаңа жүйедегі мәні - қалдықтарды ең соңғы қалдықтан бастап бөлуге кері бағытта жинай отырып q жүйесіндегі сан ретінде тізбектеп жазудан тұрады.

Мысал: 75 санын ондық жүйеден екілік, сегіздік және он алтылық жүйеге ауыстырайық:

Жауабы: 75 ₁₀ = 1 001 011 ₂ = 113 ₈ = 4B ₁₆ .

75 2 75 8 75 16

1 37 2 3 9 8 (В16) 11 4 16

1 18 2 1 1 8 ④ 0

0 9 2 ① 0

1 4 2

0 2 2

0 1 2

① 0

Дұрыс ондық бөлшекті басқа позициялық санау жүйесіне ауыстыру

Берілген дұрыс ондық бөлшек санды - F негізі q болып келген санау жүйесіне ауыстыру үшін сол F - ті q- ге ондық жүйеде көбейту керек. Сонан шыққан көбейтіндінің үтірден кейінгі бөлшегін қайтадан q -ге көбейту қажет, т. с. ж., көбейту процесі көбейтіндінің бөлшегі 0 -ге тең болған кезде немесе F санының q жүйесіндегі қажетті дәлдігі табылған кезде тоқтатылады. F санының жаңа жүйедегі бөлшек мәні - көбейтіндінің бүтін бөлігін оларды алу бағытында тізбектеп q -жүйесінде жазудан тұрады. Егер F санының k цифры табылған болса, онда оның абсолюттік қатесі q ^-(k+1) / 2 санына тең болады .

Мысал: 0, 36 ₁₀ санын ондық жүйеден сегіздік және он алтылық жүйеге ауыстырайық:

Бүтін және бөлшегі бар аралас сандарды ондық жүйеден басқа бір санау жүйесіне ауыстыру - оның бүтін бөлігі мен бөлшегі үшін жоғарыдағы ережелерге сәйкес жеке-жеке орындалады.

Мысалдар:

а) 181, 3125 ₁₀ → x ₈ : Бұл санның бүті бөлігі мен бөлшегін жеке-жеке сегіздік жүйеге түрлендіреміз де, шыққан сандарды біріктіріп жазамыз.

181 ₁₀ → x ₈ : 0, 3125 ₁₀ → x ₈ :

181: 181

8: 8

Жауабы18110= 2658:

Жауабы

181 ₁₀ = 265 ₈

0: 0

31258: 3125

Жауабы0, 312510=0, 248:

Жауабы

0, 3125 ₁₀ =0, 24 ₈

181: 176

8: 22

: 8

Жауабы18110= 2658: 2

0: 5000

181: 5

8: 16

: 2

Жауабы18110= 2658: 4

181:

8: 6

Жауабы18110= 2658:

Сонымен, толық жауабы: 181, 3125 ₁₀ → 265, 24 ₈

ә) 622, 45 ₁₀ → x ₁₆ : Бұл санның да бүтін бөлігі мен бөлшегін жеке-жеке он алтылық жүйеге түрлендіреміз де, шыққан сандарды біріктіріп жазамыз.

622 ₁₀ → x ₁₆ : 0, 45 ₁₀ → x ₁₆ :

622: 622

16: 16

Жауабы62210= 26Е16:

Жауабы

622 ₁₀ = 26Е ₁₆

0: 0

4516: 45

Жауабы0, 4510= 0, 2В3316:

Жауабы

0, 45 ₁₀ = 0, 2В33 ₁₆

622: 48

16: 38

: 16

Жауабы62210= 26Е16: 2

0: 70

622: 142

16: 32

: 2

Жауабы62210= 26Е16: 11

0: 2

622: 128

16: 6

Жауабы62210= 26Е16: 3

0: 2

622: 14

16:

Жауабы62210= 26Е16: 3

0: 2

Толық жауабы: 622, 45 ₁₀ → 26Е, 2В33 ₈

б) 23, 125 ₁₀ → x ₂

23 ₁₀ → x ₂ : 0, 125 ₁₀ → x ₂ :

23: 23

2: 2

23: 22

2: 11

: 2

23: 1

2: 10

: 5

: 2

23:

2: 1

: 4

: 2

23:

: 1

: 2

: 1

23:

: 0

23:

0: 0

1252: 125

0: 0

1252: 25

0: 0

1252: 5

0: 1

1252: 0

Жауабы: 23, 125 ₁₀ = 10111, 001 ₂ .

Екілік (сегіздік, он алтылық) санды ондық жүйеге ауыстыру

Негізі q ( q = 2, 8 немесе 16) болып келген х санын ондық санау жүйесіне ауыстырып, оны

x _q = (a _n a _n-1 . . . a ₀ , a _-1 a _-2 . . . a _-m ) _q

түрінде алу мынадай көпмүшелікті ондық арифметика көмегімен есептеуге келіп тіреледі:

x ₁₀ = a _n q ⁿ + a _n-1 q ^n-1 + . . . + a ₀ q ⁰ + a _-1 q ^-1 + a _-2 q ^-2 + . . . + a _-m q ^-m

Сандарды кез келген жүйеден ондық жүйеге ауыстыру үшін берілген жүйенің негізін қолдана отырып, дәрежелік қатар құрылады да, соның қосындысы есептеледі.

Мысалдар.

Бүтін сандарды бір санау жүйесінен екінші санау жүйесіне

түрлендірудің жалпы тәртіптері

Тек компьютерде қолданылатын санау жүйелерін - ондық, екілік, сегіздік және он алтылық сандарды қарастырамыз. Мысал ретінде кез келген ондық санды, мысалы: 46-ны алып, осы сан үшін барлық жүйелерге түрлендіру тәсілдерін қарастырайық. Түрлендіру тәртібін төмендегі сурет бойынша анықтаймыз:

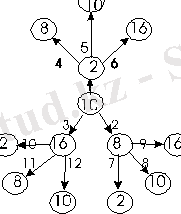
2. 2 сурет. Санау жүйелерін бірінен біріне түрлендіру тәртібі

Бұл суретте мынадай белгілеулер қолданылған:

дөңгелек ішінде санау жүйесінің негізі жазылған;
тілсызықтар түрлендіру бағытын көрсетеді;
тілсызық маңындағы нөмір 2. 3 кестедегі мысалдың сәйкес нөмірін көрсетеді.

Мысалы: 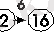белгісі сандарды екілік жүйеден он алтылық жүйеге ауыстырудың кестеде нөмірі 6-ға сәйкес екендігін көрсетеді.

2. 3 кесте

Бүтін сандарды түрлендіру кестесі

№

Түрлендіру

№

Түрлендіру

№: 1

Түрлендіру:

10 → 2

46 2

0 23 2

1 11 2

1 5 2

1 2 2

0 1

Жауабы: 101110 ₂

№: 4

Түрлендіру:

2 → 8

101110 ₂ = 101 110 = 56 ₈

5 6

Жауабы: 56 ₈

№: 2

Түрлендіру:

10 → 8

46 8

6 5

Жауабы: 56 ₈

№: 5

Түрлендіру:

2 → 10

5 4 3 2 1 0

1 0 1 1 1 0 ₂ = 2 ⁵ + 2 ³ + 2 ² + 2 ¹ = 46 ₁₀

Жауабы: 46 ₁₀

№: 3

Түрлендіру:

10 → 16

46 16

(Е ₁₆ ) 14 2

Жауабы: 2Е ₁₆

№: 6

Түрлендіру:

2 → 16

101110 ₂ = 10 1110 ₂ = 0010 1110 ₂ = 2E ₁₆

2 E

Жауабы: 2E ₁₆

8 → 2

56 ₈ = 101 110 ₂ = 101110 ₂

Жауабы: 101110 ₂

16 → 2

2E ₁₆ = 0010 1110 ₂ = 101110 ₂

2 E

Жауабы: 101110 ₂

7: 8

8 → 2568= 101 1102= 1011102Жауабы: 1011102:

8 → 10

1 0

5 6 ₈ = 5 ⋅ 8 ¹ + 6 ⋅ 8 ⁰ =

= 46 ₁₀

Жауабы: 46 ₁₀

10: 11

16 → 22E16= 0010 11102= 10111022 EЖауабы: 1011102:

16 → 8

2E ₁₆ = 0010 1110 ₂ = 101 110 ₂ = 56 ₈

2 E 5 6

Жауабы: 56 ₈

7: 9

8 → 2568= 101 1102= 1011102Жауабы: 1011102:

8 → 16

5 6 ₈ = 101110 ₂ = 10 1110 ₂ =

= 0010 1110 ₂ = 2E ₁₆

2 E

Жауабы: 2E ₁₆

10: 12

16 → 22E16= 0010 11102= 10111022 EЖауабы: 1011102:

16 → 10

1 0

2 E ₁₆ = 2 ⋅ 16 ¹ + E ⋅ 16 ⁰ = 32 + 14⋅ 1 =

= 46 ₁₀

Жауабы: 46 ₁₀

Аралас сандарды түрлендіруден тағы да бірсыпыра мысалдар келтірейік.

1) 703, 4 ₈ → х ₁₀ : 703, 4 ₈ = 7 ⋅ 8 ² + 0 ⋅ 8 ¹ + 3 ⋅ 8 ⁰ + 0 ⋅ 8 ^-1 + 4 ⋅ 8 ^-2 = 451, 0625 ₁₀

2) B2E, 4 ₁₆ → х ₁₀ : B2E, 4 ₁₆ = 11 ⋅ 16 ² + 2 ⋅ 16 ¹ + 14 ⋅ 16 ^-1 = 2862, 25 ₁₀

3) 110001, 1101 ₂ → х ₈ : 001 101 111 001, 110 100 = 1571, 64 ₈

1 5 7 1 6 4

4) 011, 100111 ₂ → х ₁₆ :

0111 1011, 1001 1100 = 7FB, 9 ₁₆

7 F B 9 C

5) 27, 333 ₁₀ → х ₂ : Жауабы: 11011, 0101 ₂

a) Бүтін бөлігі: ә) Бөлшегі:

27: 27

2: 2

27: 26

2: 13

: 2

27: 1

2: 12

: 6

: 2

27:

2: 1

: 6

: 3

: 2

27:

: 0

: 2

: 1

27:

: 1

0,: 0,

3332: 333

0,: 0

3332: 666

0,: 1

3332: 332

0,: 0

3332: 664

0,: 1

3332: 338

Сонымен 27 ₁₀ = 11011 ₁₀ ; 0, 333 ₁₀ = 0, 101 ₂ .

6) Сегіздік жүйеден оналтылық жүйеге сандарды түрлендіру екілік жүйе арқылы сан разрядтарын үшке (триада) және төртке (тетрада) бөліп қарастыру жолымен орындалады.

175, 24 ₈ → х ₁₆ :

1 7 5, 2 4 ₈ = 001 111 101, 010 100 = 1 111 101,

010 1 ₂ = 0111 1101, 0101 ₂ = 7D, 5 ₁₆

7) 10101101, 101 ₂ → х ₁₀ : 10101101, 101 ₂ = 1⋅ 2 ⁷ + 0⋅ 2 ⁶ + 1⋅ 2 ⁵ + 0⋅ 2 ⁴ + 1⋅ 2 ³ + 1⋅ 2 ² + 0⋅ 2 ¹ + 1⋅ 2 ⁰ +