Динамикалық қатардың түрлері

Динамикалық қатардың түрлері.

Бір қатарларда деңгейлер абсолютті көрсеткіштер мен (көмір өндірудің жылдық көрсеткіші), басқа орташалармен (ҚР дағы жылдық бидай өнімінің көрсеткіші) немесе қатыстылармен (жылдық рентабельділік деңгейі, пайызбен (%) көрсетіледі.

Түріне байланысты динамикалық қатар 3 түрге бөлінеді.

• абсолютті
• қатысты
• орташа

Динамиканың қатысты көрсеткішінің қатарлары белгілі-бір көрсеткіштің өсу деңгейлеріне анықтама бере алады.

Динамикалық көрсеткіштің қатарларының деңгейлері белгілі-бір уақытқа немесе кезеңге қатысты болады. Мысалы: жыл бойындағы шаруашылық фермерлердің сандары. Мысалы: жылдар бойы мұнай өндіру жыл соңында берілген қорытындының көрсеткіші болып табылады. Осыдан қатарлар моменттік және интервалдық болып бөлінеді.

Моменттік қатар дегеніміз-бұл көрсеткіштің мәні белгілі-бір уақыт аралығына байланысты болып келетін деңгей.

Интервалды қатар дегеніміз-бұл белгілі-бір кезең ішіндегі көрсеткіштің мәнін анықтайтын деңгей. Олардың деңгейлерін қосу және бөлу арқылы анықтаймыз. Мұнай өндірудің айлық көрсеткішін біле отырып, біз жыл бойындағы немесе тоқсан бойындағы мұнай көлемін таба аламыз. Мысалы:Бір күнде жөнделетін жол километрмен (км) берілген. Осы арқылы біз 1 ай бойындағы немесе 10 (он) күн ішіндегі жөнделген жол көлемін таба аламыз.

Деңгейлердің сәйкестігі мен динамика қатарларының беттесуі.

Динамика қатарына қойылатын талаптардың бірі - бұл сәйкестік.

Талаптары:

• мәліметтерді жинақтау әдістемесінің өзгеруі. Жыртылған жерден жиналған өнім көлемі, өндірістегі бір жұмысшының немесе жұмыскердің өндірген өнім көлемі.
• есепке алу уақытысын өзгерту. Бірінші қаңтардағы немесе бірінші қазандағы мал басының саны.
• өлшем бірліктерінің өзгеруі. Квадраттық метрлер және бағалар.
• бағаның бір бірлікке келтіру.

Динамикалық қатарындағы деңгейлерінің өзгеру көрсеткіштері.

Уақыт аралығындағы көрсеткіштің даму жылдамдығының анализі статистикалық көрсеткіштер көмегімен анықталады, бұл көрсеткіштер деңгейлерді бір-бірімен салыстыру арқылы анықталады. Бұларға абсолюттік өсімше, өсу қарқыны және өсімше қарқыны өсімшенің 1% -тік абсолюттік мәні жатады.

Абсолюттік өсімше -(∆у) қатардағы екі деңгейдің арасындағы айырмашылық болып табылады. Салыстыру базасына байланысты тізбектелген және базистік болуы мүмкін. ∆yi=Yi-Yi-k егер к =1 тең болса, абсолюттік өсімшенің өзгеруі тізбектелген болып табылады.

Өсу қарқыны-бұл қатысты көрсеткіш. Келесі мәліметтен алдыңғы мәліметтің қатынасына тең болады. Өсу коэфициенті арқылы берілген деңгей базистік деңгейден қанша есе үлкен екенін көрсетеді. Базистік деңгейдегі мақсатты анықтау үшін бәріне бірдей тұрақты бір деңгей берілуі мүмкін немесе сол деңгейдің алдындағы деңгейі берілуі мүмкін.

Тy1= $\frac{Yi}{Y1}$ $\frac{Yi}{Y1}$ 100 базистік өсу қарқыны немесе

Тyi-1= $\frac{Yi}{Yi - 1}$ $\frac{Yi}{Yi - 1}$ 100 тізбектік өсу қарқыны

Өсімше қарқыны-бұл қатысты көрсеткіш. Берілген деңгей басқа деңгейге қарағанда қанша пайызға көп екендігін көрсетеді, оны екі формуламен есептеуге болады.

Tnp=Tp-100% немесе Tnp= $\frac{\mathrm{\Delta}Y}{Yi - 1}$ $\frac{\mathrm{\Delta}Y}{Yi - 1}$ 100%

Динамикалық қатардағы орташа көрсеткіштің шегерімі.

Динамикалық қатардың жалпы мінездемесіне ең алдымен pY орташа деңгейін жатқызамыз ол орташа хронологиялық деп аталады. Динамикалық қатардың әр түріне орташа деңгей бірдей есептелмейді.

Интервалды қатардағы абсолюттік көлемі бар орташа деңгей арифметикалық әдіспен есептеледі. Мысалғы:

Y орт. = $\ \frac{\mathbb{∑}Уi}{n} = \frac{34 + 39 + 38 + 46 + 38 + 33 + 39}{7} = 38, 14$

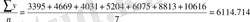
Қатардағы орташа көлемі бар орта деңгей басқа әдіспен есептеледі. Бұл қате болып саналады. Бұл қатар үшін орташа деңгей біршама басқа әдіспен есептеледі. Ол мына формула бойынша:

$\frac{\frac{Y1}{2} + Y2 + Y3 + \ldots + Yn/2}{n - 1}$ $\frac{\frac{Y1 + Yn}{2} + \sum_{i = 2}^{n - 1}{Yi}}{n - 1}$ Yорт. = $\frac{\frac{Y1}{2} + Y2 + Y3 + \ldots + Yn/2}{n - 1}$ = $\frac{\frac{Y1 + Yn}{2} + \sum_{i = 2}^{n - 1}{Yi}}{n - 1}$

Бұл формула статистикада орташа хронологиялық деген атпен танымал.

Егер орташа хронологиялық әдістегі уақыт мәліметтерінің ара- қашықтығы тең болмаса, онда оны орташа арифметикалық әдіспен есептеуге болады, уақыттағы арасындағы қашықтықты есепке ала отырып.

$\frac{\binom{Y1 + Y2}{2}t1 + \binom{Y2 + Y3}{2}t2 + \ldots + \binom{Yn - 1 + Yn}{2}tn - 1}{t1 + t2 + \ldots tn - 1}$ $\frac{\Sigma(Yi + Yi + 1) ti}{2\Sigma ti}$ Yорт. = $\frac{\binom{Y1 + Y2}{2}t1 + \binom{Y2 + Y3}{2}t2 + \ldots + \binom{Yn - 1 + Yn}{2}tn - 1}{t1 + t2 + \ldots tn - 1}$ = $\frac{\Sigma(Yi + Yi + 1) ti}{2\Sigma ti}$

Мысалғы: 2005 жылғы көмір өндіру туралы мәліметтер белгілі болсын.

Бұдан 2005 жылғы көмірдің айлық орташа қалдығы, тең:

$\frac{(34 + 38) *2 + (38 + 39) *2}{2*(2 + 2) } = 37, 25$ У =

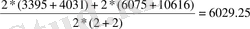
Деңгейдің орташа абсолюттік өсімшесі орташа арифметикалық жәй әдіспен есептелінеді, тізбектелген өсімше бойынша.

$\frac{Yn - Yo}{n} = \frac{39 - 34}{6} = 0, 83$ Δy=

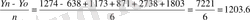
Уо- 2000 жылдан бастап өсімшені есептеудің базистік әдісі бойынша. Сондықтан кезең саны 6. Анализде динамикалық қатардағы орташа өсу қарқынын есептеуге ерекше көп көңіл бөлінеді. Орташа өсу қарқынын тізбегіндегі орташа геометриялық пен теңестіріп есептеу жиі кездеседі, әр кезеңдегі алдыңғы деңгейге қатыстығы бойынша.

$\sqrt[n] {k_{1\ }}k_{2\ldots}k_{n}$ Tp= $\sqrt[n] {k_{1\ }}k_{2\ldots}k_{n}$ *100%= 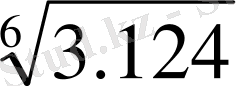= = 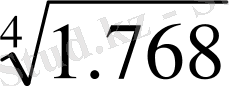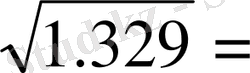1. 153 немесе 115. 3% немесе

Корт. = 1. 153

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс