Мектепте математикалық есептерді шешудің жалпы әдістерін оқытудың теориялық негіздері


ЖОСПАР
КІРІСПЕ3
1. ЕСЕПТЕР ШЫҒАРУДЫҢ ЖАЛПЫ ӘДІСТЕРІН ОҚЫТУДЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ5
1. 1. Оқыту процесіндегі есептердің ролі. 5
1. 2. Оқытуға арналған математикалық есептердің мәні. 9
1. 3. Есеп шығаруға қойылатын негізгі талаптар10
1. 4. Теориялық материалдарды игеруде шығармашылық тапсырмалар мен қызғылықты есептердің рөлі. 13
2. ЕСЕПТЕР ШЕШУДІҢ ЖАЛПЫ ӘДІСТЕРІ. 14
2. 1. Есептер шешудегі анализ бен синтез. 14
2. 2. Математика есептерін шығаруды үйретудің әдістері15
2. 2. 1. Синтетикалық әдіс15
2. 2. 2. Аналитикалық әдіс15
2. 2. 3. Салу есептеріндегі аналитикалық әдіс17
2. 2. 4. Алгебралық талдау18
2. 2. 5. Есеп шешудің арнаулы әдістері19
2. 3. Оқушыларды есеп шығаруға үйрету21
Қорытынды25
Пайдаланылған әдебиеттер27
КІРІСПЕ
Зерттеудің өзектілігі. ХХІ ғасырда әлемдік өркениет төрінен орын алып, Қазақстанның жан-жақты дамуының бірден-бір жолы білім мен ғылымды әр қырынан меңгеру қажет болып отырғаны белгілі. Елбасы Н. Назарбаев Білім мен Ғылым қызметкерлерінің ІІІ съезінде: «Құрылымдық өзгерістер мұғалім кадрларын одыра отырып, дамытумен қамтамасыз етілуі тиіс. Жаңа формацияның педагогы қажет. Мұғалімдердің жаңа ұрпағы білім деңгейі жөнінен әрдайым саналып келгеніндей біршама емес, әлдеқайда жоғары болуы тиіс, бұл уақыттың талабы» дей келе, өзінің Қазақстан халқына жолдауында болашақ, келесі ғасырға, жаңа мыңжылдыққа өтетін құндылықтар туралы былайша ой толғады: « . . . Біз өзіміздің болашағымызды және баларымызды қандай күйде көргіміз келеді, осыны айқындап алатын уақыт жетті. Біз ненің іргесін тұрғызғымыз келетінін, таңдап алған мақсатымызға алып келетін өз дамуымыздың траекториясы, даңғылы қандай болуы тиіс екенін анық білуге және ұғынуға тиіспіз». Білім беруді қоғамның әлеуметтік-экономикалық, мәдени құндылықтарынан, ұлттық дәстүр, рухани негізден бөле-жара қарауға болмайды, сонымен қатар онда ғылым мен техниканың, педагогиканың соңғы жаңалықтары да барынша ескрілуі тиіс. Сондықтан да қоғамда болып жатқан әртүрлі шаралардың негізгі мақсаты бір - ол заман ағымынан қалып қоймай, өркениетті мемлекет құруға ұмтылыс жасау. Үздіксіз өзгеріп тұрған заман адамнан сол заман талабына сай білім алып, жаңа істерді меңгеруді, оқу-тәрбие үрдістерін жаңаша дамытып, жаңа педагогикалық технологияларды жүйелі пайдалануды талап етеді. Бұл үрдіс - қазіргі қоғамдағы жалпы білім беру қызметіне жаңаша қарауды, қол жеткен табыстарды сын көзбен бағалай отырып саралауды, жасөспірімдердің шығармашылық қабілетін дамытуды, сабаққа деген қызығушылығын арттыруды, оқытудың озық технологияларын меңгеруді талап етеді. Қазіргі білім беру саласында оқытудың технологияларын меңгермейінше сауатты, жан-жақты маман болуы мүмкін емес. Педагог білім беру іс-әрекетінің субъектісі ретінде оқытудың небір жаңа әдіс-тәсілдерін, формаларын жүзеге асырушы басты тұрға, сондықтан білім берудің барлық оңды өзгерістер мұғалімнің жаңаша ойлау тәсілімен, жаңа шығармашылық іс-әрекеттірімен, өзіне және балаларға деген жаңа қатынасымен, жаңаша педагогикалық гуманистік құндылықтарымен тікелей байланысты болады.
Бәсекеге қабілетті жеке тұлға тәрбиелеудің негізгі тиімді жолы жеткіншектерге білім берудің әрбір сатысындағы пәндік білім беру мазмұны мен әдістемесін жетілдіру жолдарын жан-жақты дамыту деп есептейміз. Мектеп пәндерінің ішінде математикалық білімнің орны ерекше.
Математиканы оқыту процесін ұйымдастыруда мазмұнды есептердің ішінде экономикалық мазмұнды есептер шығару негізінде оқушылардың экономикалық ойлауын қалыптастыру бүгінгі өмір талабына сай азамат тәрбиелеудің негізгі жолдарының бірі деуге болады. Себебі мектеп оқушыларының болашақ өміріндегі өндірістік қарым-қатынастардың әрекет ету зандылықтары олардың жеке қызметіне тікелей байланысты
Оқыту әдістері, тәсілдері және құралдары туралы ұғым.
Әдіс - оқу-тәрбие жұмыстарының алдында тұрған міндеттерді дұрыс орындау үшін мұғалім мен оқушылардың бірлесіп жұмыс істеу үшін қолданатын тәсілдері. Әдіс арқылы мақсатқа жету үшін істелетін жұмыстар ретке келтіріледі. Оқыту әдістері танымға қызығушылық туғызып, оқушының ақыл-ойын дамытады, ізденуге, жаңа білімді түсінуге ықпал етеді. Оқытуда ең басты нәрсе - оқушылардың танымдық жұмыстары. Оқыту әдістері ең анық фактілерді білуді қамтамасыз етеді, теория мен тәжірибенің арасын жақындатады.
Тәсіл - оқыту әдісінің элементі. Жоспарды хабарлау, оқушылардың зейінін сабаққа аудару, оқушылардың мұғалім көрсеткен іс-қимылдарды қайталауы, ақыл-ой жұмыстары тәсілге жатады. Тәсіл оқу материалын түсінуге үлес қосады.
Зерттеу мақсаты: Есептер шығарудың жалпы әдістерін оқытуда теориялық тұрғыдан негіздеу.
Зерттеу міндеттері:
- мектепте есептер шығарудың жалпы әдістерін оқытудың мүмкіндіктерін анықтау;
- мектепте есептер шығарудың жалпы әдістерін оқытуда пайдалану, жетілдіру және соның негізінде әдістемелік ұсыныстар беру.
Жұмыстың құрылымы мен көлемі:
Курстық жұмыс кіріспеден, екі тараудан, қорытыныдан және пайдаланған әдебиеттер тізімінен тұрады.
1. ЕСЕПТЕР ШЫҒАРУДЫҢ ЖАЛПЫ ӘДІСТЕРІН ОҚЫТУДЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ
1. 1. Оқыту процесіндегі есептердің ролі.
Әрбір нақты математикалық есеп бірнеше педагогикалық, дидактикалық, оқытудың мақсаттарының іске асуын, олардың дамуына ықпал ету мақсатын алға қояды. Бұл мақсаттар есептің мазмұны, не қолданылуы арқылы іске асады. Мұғалім есептер арқылы дидактикалық талаптар қойғанда есептің оқыту процесіндегі мәнін көрсетеді.
Есеп мазмұнынан және оны қолданудың дидактикалық талаптарынан мыналарды бөліп алуға болады.
2. 1. Математикалық есептердің оқытудағы ролі (білім, білік, дағды) .
1. Математикалық ұғымдарды меңгеру үшін есептер шешіледі.
Математикалық ұғым қалыптастыру ұғыммен оның анықтамасы мен қасиетімен көп жұмыс жүргізу керек. Бұларды құрғақ жаттаудан ұғым қалыптаспайды. Көптеген жаттығулар орындап есептер шешкенде ұғым қалыптастырғанда оқушының нақты білімі болады. Мысалы, логарифм ұғымын меңгеруде көрсеткіштік функция мен оның мәндерін логарифмдік формада жазу және керісінше, сондай-ақ белгісізді логарифмге тәуелді жай логарифмдік теңдеулер шешу, бұлардың негізінде нақты мысалдар арқылы логарифмнің анықтамасын қалыптастыру,
а logx =x, a>0, a≠1, x>0.
Бұл арада мынадай есептер шешу пайдалы:
1) Мынадай анықтама дұрыс бола ма?
а x =x теңдігін қанағаттандыратын дәреже көрсеткіш а негіздегі в санының логарифмі деп аталады.
2) Келесі тұжырымды талдаңдар: “Берілген санның берілген негіздегі логарифмі дәреже көрсеткіш болып табылады”. Осы сөйлем логарифмнің анықтамасы болу үшін мұны қалай анықтайды.
2. Математикалық символиканы меңгерудегі есептердің ролі.
Математиканы оқытудың бір мақсаты математиканың тілін, символикасын білу. Жай таңбалар, символдар бастауышта және IV-V сыныпта (амал таңбалары, теңдік, теңсіздік, жақша, бұрын белгісі және оның шамасы, параллелдік т. б. ) Үйрететін символдарды дұрыс қолдану үшін есептер шешіледі. Есептердің мағынасы мен шығару жолы жақшаны дұрыс қолдануға үйретеді.
Мына есептерде жақша қандай роль атқарып тұр, қандай өрнектерде жақша қандай роль атқарып тұр, қандай өрнектерде жақша амалдардың орындалу ретін өзгертпейді.
(1)
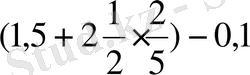 (2)
(2)
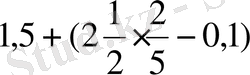
(3)
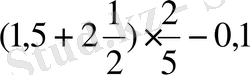 (4)
(4)
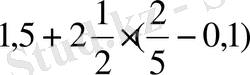
(5)
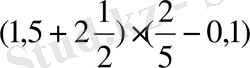
- Амалдардың орындалу ретін түсіндіріңіздер және жақша қандай роль атқарады.
(1)

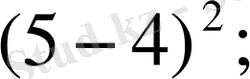
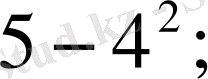
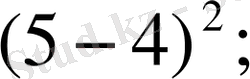
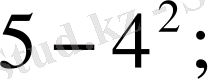

(2)
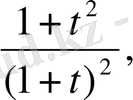 t=-8, (3)
t=-8, (3)
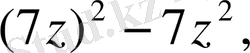 мұндағы
мұндағы
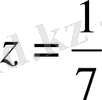 .
.
Символиканы үйренуде басты мәселе есептер шешу барысында оны дұрыс қолдану.
3) Дәлелдеуді оқытуға қажетті есептер.
Математиканы оқытудың маңызды міндеттерінің бірі оқушыларға дәлелдеуді үйрету. Жай есептердің өзі дәлелдеуден басталады. Элементар есептер сұрақтар зерттеуді қажетсінеді. Мұндай есептердің жауабын іздеу олардың шындығын іздеуге келеді.
Есептер мен сұрақтар өзінің шешімін берілгеннен дәлелдеуге тиісті ұғымға логикалық қадам жасап ілгерілеу б. т. Күрделі есептер бірнеше логикалық тізбектен тұрады. Есептер шешудің мақсаты - үйреніп отырған ұғымды нақтылау, соның табиғатын түсіну, оның әртүрлі байланыстарын қарау . . . есептер мен сұрақтар символика мен математика тілін меңгеру үшін керек. Есептер - сұрақтар.
2. x>y, бұдан міндетті түрде х 2 >y 2 бола ма?
3. Екі биссектриса перпендикуляр бола ма? Екі биіктік ше?
Дәлелдеу кезінде есеп желісінен сөзбен символды, олардың бірігуінен тұратын кейбір элементтерді қалдырып кетуге негізделіп құрастырылған жаттығулардың маңызы зор. Осындай жаттығулар тіл сабақтарында көп қолданылады.
4. Тік бұрышты үшбұрышта гипотенузаның ұзындығы оның катетінен ұзын болатынын дәлелдейік.
∆ΑΒС - тік бұрышты үшбұрышын қарастырамыз:
∠C=90 0 , АС және . . . - оның катеттері, . . . - гипотенуза. С нүктесі . . . деп аталады.
В
С А
В нүктесі . . . жатқандықтан ВС . . . СА
Перпендикулярлық теорема бойынша және . . . ВС . . . АВ.
Дәл осылайша, нүкте . . . деп аталады, . . . А нүктесінің ВС түзуінің. Демек, . . . перпендикуляр . . .
Сондықтан . . . < … ( … теореманың негізінде) .
4-5 сыныпта математикадан дәлелдеу есептері мүлдем жоқ.
5. а≠0, в≠0 болсын. Ал а+в≠0 дұрыс па?
6. Рационал сандардың көбейту ережесі және оң сандарды көбейтудің ауыстырымдылық заңын қолданып кез келген екі рационал сан үшін осы заңның орындалатынын дәлелдеу керек.
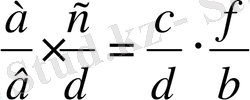 .
.
4-5 сыныптар алгебрасында теңбе-теңдіктер мен теңсіздіктерді функциялардың қасиеттеріне сүйеніп дәлелдеу есептері өте жиі қолданылады.
7. Егер х 2 +px+q=(x+x 2 ) теңдігі ақиқат болса, онда p 2 -4q=0 теңдігі ақиқат екенін дәлелдеңдер. Бұл сөйлемге кері сөйлемді тұжырымдаңдар.
4-5 сыныптар геометриясында дайын сызбаларды қолданып дәлелдеу практикасы бар. Бұл да дәлелдеуді оқытуға аса қажетті.
8.
1) Берілген BD⊥AC, AB=BC. Дәлелдеу керек: AD=DC?
2) Берілгені: BD⊥AC, AD=DC; Дәлелдеу керек: AB=BC?
В
Кейбір геометриялық теңдіктерді
дәлелдеуде ұсынылады. Стереометрияда да
көптеген теңдіктер бар.
А D C
9-11 сыныптарда математиканың барлық тарауларын қарастыратын теңдіктер оқытылады.
9. Рационал сандар арасынан квадраттары
1) 3; 2) 5; 3) 6; 4) 7; 5) 10 сандарына тең болатын сандар болмайтынын дәлелдеңдер.
10. Ғ(х) =cos 2 x және Ғ(х) =-sin 2 x функциялары f(х) =-sin2x функциясының алғашқы образы екенін дәлелдеңдер.
Мұндағы Ғ(х) =Ғ(х) +1.
4) Математикалық білік және дағды қалыптастыруға арналған есептер (§4. 3 айтылады) .
5) Математикалық жаңа фактілерді үйренуге қажетті идеялар мен методтар жаңа ұғымдармен методтарды ендіруге керекті есептер, проблемалық ситуация туғызуға арналған есептер - оқыту ролін атқарады. Есептер бұл арада күрделі теореманы дәлелдеуге дайындық ролін атқарады.
Квадрат теңдеулерді шешу тәсілдерін үйрену үшін проблемалық жағдай туғызуда есептерді пайдаланады. Мысалы,
11. Теплоход өзен ағысы бойынша 48 км жүрсіп кейін қайтты, бүкіл жолға 5 сағ уақыт жіберді. Өзен ағысының жылдамдығы 4 км/сағ. Теплоходтың меншікті жылдамдығын табыңдар.
Егер теплоходтың меншікті жылдамдығын V км/сағ десек,
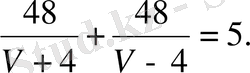 5V
2
-96V-20, V≠±4.
5V
2
-96V-20, V≠±4.
Квадрат теңдеуді шешу тәсілдері осылайша проблемалық жағдайда қарастырылады.
12. алғашқы бағасы 1 теңге бұйым 4 жыл ішінде әр жылы 5% арзандаған болса, оның бағасы енді қанша болды?
1(
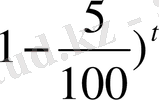 , t=4. A=1(
, t=4. A=1(
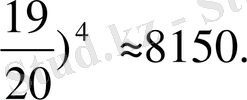
13. Берілгені AB=BC, AM //BN, BM//CN. Д/к. ∆ABM=∆BCN
Бұл есепті шешу Фалер теоремасын
жеңілдетеді.
Есептер шешу арқылы оқушының ойын дамыту.
1) Есеп шығару кезіндегі ойша орындау мен қабылдау, еске түсіру.
Математикалық есептерді шығару кезінде көптеген ойша орындалатын дағдылар қажет болады.
Есептің берілгендеріне талдау жасау, ізделінді мен берілгендерді, бұрын өтілген есептермен салыстыру берілген жағдайдағы қасиеттерді анықтау, қарапайым модельдерді құрастыру, ойша экспериментті іске асыру, синтездеу, есеп шығаруға қажетті информацияны таңдау, оны бір жүйеге келтіру, бұл информацияны қысқаша текст, символика, график түрінде тұжырымдап есеп шығаруға қолдану. Есеп шешімін жалпылау, берілгендер арасындағы ерекше жағдайды зерттеу. Есеп шығару кезінде осы заманғы психологияның жетістіктерін пайдалану. Психологтары есептерді бір сыныптың әр оқушылары әр түрлі формада түсінеді. Математикаға қабілетті оқушы есептердің дербес элементтерін, бір тұтас комплекстегі өзара байланысты элементтерді, комплекстегі әрбір элементтердің ролін түсінеді. Орташа оқушы есептің дербес элементтерін ғана түсіне алады. Сондықтан есептерді шешуді үйреткен кезде есеп элементтердің арасындағы қатысты арнайы талдау керек. Бұл есептер шартын талдауға қажетті тәсілдерді таңдап алуға мүмкіндік береді. Есеп шығару кезінде көбінесе бұрын өтілгендерді еске түсіруге тура келеді. Қабілетті оқушы ең қажетті информацияны «жалпыланған, структурасы қабаттасқан» информацияны есінде қалдырады. Есте сақталған информация мида асып төгіледі, есте қалғандары пайдалануға оңай, оңай есте қалады. Есептер шешу кезіндегі жалпылау тек ойды дамытып қана қоймай, еске сақтауды да және «жалпыланған ассоциацияны» қалыптастырады. Есеп шығару кезінде осылардың бәрін ескеру керек.
2) Ойлауды оқыту.
Математикалық есептер мен жаттығулардың тиімділігі көбінесе оқушылардың есептер шешу кезіндегі творчестволық белсенділігінің дәрежесіне тікелей байланысты. Есеп оқушылардың сабақтағы ойлау қызметін белсенді қалыпқа келтіреді. Есептер оқушылардың ойын оятып, оны жұмыс істеуге ойлануға мәжбүр етеді, сол арқылы дамып жетіледі.
Оқушылардың ойын дамытқанда - салу, түрлендіру, тұжырымдарды еске сақтау арқылы дәл ойлауға, талқылай білуге, фактілерді қарастыра білуді, жалпы және әр түрлі ой қорытындысын жасауды үйренеді.
1. 2. Оқытуға арналған математикалық есептердің мәні.
Математиканы оқыту процесінде есептердің сан қырлы және зор мәні бар.
- (а) Математикалық есептердің білім берерлік мәні.
Математикалық есептерді шеше отырып, оқушылар көптеген жаңа мәселелерді таниды: есеп шартында жазылған жаңа жағдайлармен танысады, математикалық теорияның есептер шешуге қолданылуын, есептер шешудің жаңа әдістерін танымдық немесе есептер шешуге қажетті математиканың жаңа бір саласымен танысады, т. б. Басқа сөзбен айтқанда оқушы математикалық есептерді шешу барысында тереңдетеді. Белгілі бір класқа жататын есептер тобын шешудің әдісін игеру арқылы оқушыларда есептер шеше білу, яғни жеткілікті түрде жаттығу арқылы дағды қалыптастырып, математикалық білімін көтереді.
1. 2 (б) Математикалық есептердің практикалық мәні.
Математикалық есептерді шешу барысында оқушы математикалық білімдерін практикалық қажеттіліктерге пайдаланады, өзінің болашақтағы практикалық қызметіне (қажетті) керекті істермен айналысады. Практикалық қажеттілігі бар барлық конструкторлық есептерде математикалық есептер шешуге тура келеді. Процестерді сипаттап жазумен зерттеу математикалық аппаратты қолданбай, яғни математикалық есептеулерсіз мүмкін емес. Математикалық есептер физикада, химияда, биологияда, электротехника мен радиотехникада, ең алдымен олардың теориялық негіздерін түсіндіруге қажет. Бұл есептерді шешкенде көбінесе физикалық, химиялық, географиялық және техникалық-практикалық мәні бар есептер қарастыру қажетсінеді.
1. 3 (в) Оқушылардың ойлана білу дағдысын дамытудағы математикалық есептердің мәні.
Математикалық есептер шешу оның шартында берілгендер мен іздендіні салыстыруға, әсіресе берілгендерді, фактілерді керісінше салыстыруға, проблемалар мен қорытынды бір-бірінен ажыратыға мүмкіндік береді. А. Я. Хинчиннің айтуынша математикалық есептер оқушыларды дәлелді дұрыс ойлауға үйретеді. Есептер толығынан дәлелді, белгілі заңдар негізінде жалпы қорытындылар жасайды, дәлелді аналогияға сүйеніп, барлық жағдайларды қарастырады.
1. 4 Математикалық есептерді шешу арқылы ерекше ойлау стилі, ойымыздың формальді-логикалық схемасы, ойдың орнықтылығы, ойлау жолының дәлдігі, символиканы қолдана білу, еске сақтау, көз алдына келтірудің дәлдігіне үйретеді.
Математикалық есептердің тәрбиелік мәні
Есептер өзінің мазмұны арқылы тәрбиелейді. Қоғам дамуына қарай есеп мазмұны да өзгереді. Россияның революциядан бұрынғы есептер жинақтарында және қазіргі капиталистік елдерде сатып алу, сатып беру кезінде табыс табу, азартты ойындар туралы есептер бар.
1. 3. Есеп шығаруға қойылатын негізгі талаптар
Есеп шығаруға төмендегідей талаптар қойылады:
а) Қатесіз шығару; ә) негіздеу (дәлелдеу) ; б) толық шығару; в) мүмкіндігінше тиімді жолмен шығару; г) есепті қаттау (оформление) .
а) «Есеп қатесіз шығарылу керек».
Бұл негізгі талап. Оқушылар есеп шығару кезінде алгоритмдік, логикалық, сызбалық, терминологиялық, шындықты бұрмалау сияқты қателер жібермеу. Енді оқушылар жиі жіберетін қателік.
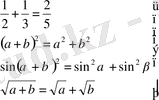 - алгоритмдік қателер.
- алгоритмдік қателер.
5=-5 екендігін дәлелдеу. Екі жағын квадраттаймыз, сонда 25=25
немесе
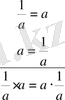
1 = 1 - логикалық қателік.
«Бүйір жағының апофемасы», «шеңбердің ауданы» т. с. с. - терминологиялық қателіктер.
Есеп: «Моторлы қайық өзен ағысымен 42 км және ағысқа қарсы 20км жол жүріп және оған 5сағ уақыт жұмсады. Егер өзен ағысының жылдамдығы 2 км/сағ болса, қайықтың өз жылдамдығы қандай?».
Есеп
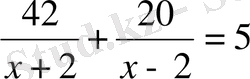 теңдеуін құру арқылы шығарылады. Теңдеу түбірлері 2/5 және 12 есеп жауабы ретінде алынса, онда шындықты бұрмалау қателігі жіберілгені. Себебі, қайықжылдамдығы өзен жылдамдығынан артық болуы тиіс, яғни 2/5 есеп шартын қанағаттандырмайды.
Жауабы:
12 км/сағ.
теңдеуін құру арқылы шығарылады. Теңдеу түбірлері 2/5 және 12 есеп жауабы ретінде алынса, онда шындықты бұрмалау қателігі жіберілгені. Себебі, қайықжылдамдығы өзен жылдамдығынан артық болуы тиіс, яғни 2/5 есеп шартын қанағаттандырмайды.
Жауабы:
12 км/сағ.
ә) Есеп шығару кезеңінің әр сатысы міндетті түрде негізделіп, дәлелденіп отыруы қажет. Яғни әрбір жаңа ой қорытындысы қандай тұжырымнан туындалады, не себепті олай деп пайымдауға хақымыз бар деген сұрақтарға мұхият жауап берілуі керек.
Мысал. Қыры а -ға тең кубтың төменгі табанының іргелес қабырғаларының ортасынан және жоғарғы табанының олармен бір жағында жатпайтын екі іргелес қабырғаларының орталары арқылы жазықтық жүргізілген. Қиманың ауданын тап.
Шешуі:
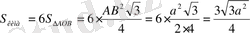
шешуі дұрыс болғанымен, қимадағы алты бұрыш неге дұрыс екендігін дәлелдеп көрсету керектігі туындайды. (1-сурет) .
б) Теңдеудің бір шешімі дұрыс табылды делік, ал оның әлі екі шешімі бар. Бірден түсінікті, есеп толық шығарылған жоқ, немесе кейде иррационал теңдеулерді шешкенде бөгде түбірлер пайда болуы мүмкін. Егер табылған шешімдердің бәрін теңдеу түбірі десек, есеп толық шығарылмағаны. Зерттеулерге арналған есептерде (әсіресе, геометриялық) мүмкін болатын барлық жағдайлар қарастырылғанда ғана, есеп толық шығарылды деп айта аламыз.
в) Есеп мүмкіндігінше тиімді, ұтымды жолмен шығарылғаны жөн. Мысал, «Үшбұрышты пирамиданың бүйір қырлары өзара перпендикуляр, олардың әрқайсысы b -ға тең. Пирамида көлемін табыңдар» (2-сурет) .
Б е р і л г е н і:
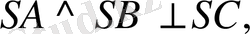
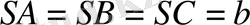 .
.
Т а б у к е р е к:
Пирамиданы аударып, табаны ретінде SBC үшбұрышын қарастырсақ, есеп әлдеқайда оңай шығарылады:
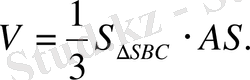
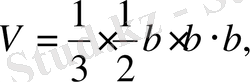
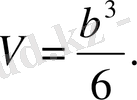
г) Есеп шығару кезеңдерін дұрыс қаттау да есепке жүктелетін талаптардың бірі болып саналады. Есеп шығару кезңдері қысқа да нұсқалы, түсінікті, сызбалар қатесіз, дәл т. б. болуы қажет. Геометриялық есептерді шығаруда есеп мазмұнына сәйкес сызба салынуы керек. Есеп шарттары, талабы айқын көрсетілуі тиіс. Шығару жолдары қысқа түрде, қажет символикаларды пайдаланып жазылуы керек. Әр жаңа тақырыпқа есептер шығарылғанда, мүмкін болатын жазу үлгісі беріліп, ілгеріде соның мұқият сақталуын қадалаған жөн. Логарифмдік теңдеуді шығару кезеңднрі:
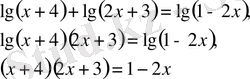
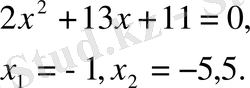
Тексеру
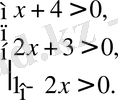 (1)
(1)
(1) -ге қойсақ, 1)

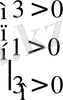 - шын
- шын
2)

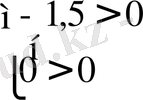 - жалған
- жалған
Жауабы:
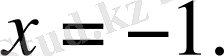
1. 4. Теориялық материалдарды игеруде шығармашылық тапсырмалар мен қызғылықты есептердің рөлі.
Оқушылар геометрия пәнін А. В. Погореловтың оқулығы бойынша бастап оқығанда көптеген қиындықтарға кездеседі. Мәселен, аксиомалардың шамадан тыс берілуі оқушыларды қатты қиналтады. Басынан № бастап пәнді түсінбегенннен кейін оқушыларға пәнге деген енжарлық, немқұрайлылық пайда болып, кейінірек геометрияны түсінбеушілікке әкеп соғады. Бірінші сабақтардан бастап оқушылар әр түрлі қарапайым фигуралармен, олардың ара-қатынастарымен танысады, жаңа терминалогия пайда болады. Алғашқы күннен бастап жаңа түсініктерді ұғындыру методикасы дұрыс ұйымдастырылса, бұл бара-бара оқушыларға қиындық келтіретіні сөзсіз. Сондықтан бірінші сабақтан бастап мұғалім әрбір жаңа түсініктің енгізу әдісін ойластыруы керек. Жетінші сынып оқушылары геометрияның негізгі түсініктері мен төменгі сыныптан таныс. Сондықтан негізгі геометрия курсын игеруге көмектесетін, бастапқы түсініктерге сүйенетін жаттығулар, тапсырмалар берілуі керек.
Бұл тапсырмалар материалды түсіндіріп жатқанда берілуі керек. Мұны оқушылар өздігінен орындайды. Мұғалім тек қана оқушылардың жұмыстарын қорытындылап, содан кейін ғана жаңа материалды түсіндіруге көшеді. Осындай жұмыстың методикалық тиімділігі мол, себебі суретті сипаттауға бүкіл сынып қатысады, осыдан оқушылардың математикалық тұрғыда сөйлей білу қабілеті қалыптасады. Оқушыларға сурет ойлап тауып, оған өзің сипаттама бер деп үйге шығармашылық тапсырма да берген жөн. Үй жаттығуларының мазмұны теориялық материалды игеруге бағытталуы қажет. Өткен сыныптардағы тақырыптардан алған білімдерін пайдаланып, оқушылар берілген фигураларға белгілер қояды, оларды орналастырады. Ал сабақтан сабаққа көшкенде суреттер күрделене түсуі қажет. Бұл жаттығулар қызықты болған жағдайда жаңа тақырып пен онда берілген ұғым оңай игеріледі. Жаттығуларға қойылатын негізгі талап - өткен сыныптарда алған білімдері негізінде оқушыларды жаңа түсініктермен тереңірек таныстырып, геометрияның жүйелілік курсына көшулеріне жол ашу.
2. ЕСЕПТЕР ШЕШУДІҢ ЖАЛПЫ ӘДІСТЕРІ.
2. 1. Есептер шешудегі анализ бен синтез.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz