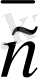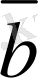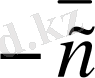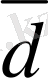Matlab-та векторлармен жұмыс және векторлық алгебра


Мазмұны
Кіріспе3
1 Matlab-та векторлармен жұмыс . . . . . . 5
1. 1 Векторларды Matlab -та енгізу . . . . . . 5
1. 2 Векторларды құру . . . . . . 5
1. 3 Векторларға матеметикалық және матеметикалық емес операциялар жасау . . . 6
1. 3. 1 Векторлық әрекет . . . . . . 7
1. 3. 2 Вектордың әрбір элементімен жұмыс. . ……8
2 Векторлық алгебра 11
2. 1. Вектор………. . . . 11
2. 2. Векторларды қосу . 12
2. 3. Векторлардың айырымы . . 14
2. 4 Векторларды санға көбейту . . . . 14
2. 5. Коллинеар және компланар векторлар . . …. . . . 15
2. 6. Базис . . . . . 16
3 Мысалдар . . . 29
Қорытынды . . . 34
Қолданылған әдебиеттер тізімі . . . 35
КІРІСПЕ
Matlab жүйесі (MATrix LABortory - Матрица лабораториясы) мәліметтер мапссивімен жұмысқа негізделген инженерлік және ғылыми есептеулерге арналған интерактивті жүйе. Matlab жүйесі дамыған математикалық және комплекстік арифметикадан тұрады.
Бұл жүйе векторлармен, матрицалармен және массивтермен операцияларды қолдайды, сингулярлы және спектралды айырылуды (разложение) іске асырады, матрица рангтарын есептейді, алгебралық полиномдармен, сызықтық емес теңдеулермен, дифференциалдық теңдеулермен және оптимизация есептерімен жұмыс жасайды, әртүрлі графиктермен тұрғызады.
2 Векторлық алгебра
2. 1. Вектор
Mатематикада, физикада, механикада кез келген құбылыс екi шамамен анықталады. Егер кез келген шама оң немесе терiс санмен анықталса, онда ол скаляр шама деп аталады. Мысалы, көлем, масса, аудан, уақыт, температура - скаляр шама. Кейбiр шамаларды анықтау үшiн олардың сандық мәнiмен қоса, бағытын да бiлу қажет, олар - векторлық шама деп аталады. Мысалы үдеу, жылдамдық, күш - векторлық шама болып табылады.
Анықтама. Вектор дегенiмiз - бағытталған кесiндi.
Берiлген вектор үлкен екi латын әрiпiмен немесе кiшi бiр латын әрiптерiмен белгiленедi. Егер вектор екi әрiппен белгiленсе, онда бiрiншi әрiп вектордың
бастапқы нүктесi
, ал екiншiсi -
соңғы нүктесi
деп аталады. Мысалы
 - вектор, A нүктесi осы вектордың бастапқы нүктесi, ал B - соңғы нүктесi, стрелка
- вектор, A нүктесi осы вектордың бастапқы нүктесi, ал B - соңғы нүктесi, стрелка
 вектордың бағытын сипаттайды, яғни вектордың бағыты A нүктеден A нүктеге бағытталған (1-сурет) . Егер вектор кiшi бiр әрiппен белгiленсе, онда сол әрiптiң төбесiне тек сызықша ғана қойылады. Мысалы,
вектордың бағытын сипаттайды, яғни вектордың бағыты A нүктеден A нүктеге бағытталған (1-сурет) . Егер вектор кiшi бiр әрiппен белгiленсе, онда сол әрiптiң төбесiне тек сызықша ғана қойылады. Мысалы,
 векторын
векторын
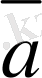 деп те белгiлеуге болады. Берiлген
деп те белгiлеуге болады. Берiлген
 векторының
үзындығы
немесе
модулi
деп, AB кесiндiсiнiң ұзындығын айтамыз және ол былай белгiленедi:
векторының
үзындығы
немесе
модулi
деп, AB кесiндiсiнiң ұзындығын айтамыз және ол былай белгiленедi:
 немесе
немесе
 .
.
E
F
B
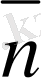
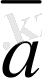 . 3
. 3
A
1-сурет
Модулдерi бiрге тең векторлар
бiрлiк
немесе
орт
векторлар
деп аталады. Берiлген
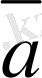 векторының орт векторы
векторының орт векторы
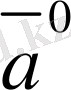 деп белгiленедi және оның бағыты
деп белгiленедi және оның бағыты
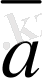 векторының бағытымен бағыттас. Жалпы
векторының бағытымен бағыттас. Жалпы
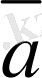 векторының орт векторын
векторының орт векторын
 деп те белгiлейдi (2-сурет) .
деп те белгiлейдi (2-сурет) .
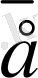
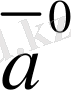

2-сурет
Аны қ тама. Екi вектор тең деп аталады, егер:
1. Oлар параллель болса (параллель түзулердiң бойында немесе бiр түзудiң бойында жатса) ;
2. Олардың бағыттары бағыттас болса;
3. Олардың модульдерi тең болса.
Екi
 мен
мен
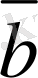 векторларының теңдiгiн былай белгiлеймiз:
векторларының теңдiгiн былай белгiлеймiз:
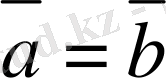 .
.
Анықтама. Егер екi вектор бiр түзудiң бойында немесе параллель түзулердiң бойында жатса, онда мұндай векторлар коллинеар векторлар деп аталады (3-сурет) .
3-сурет
Егер вектордың бас нүктесiмен соңғы нүктесi бiр нүктеде үйлессе, онда мұндай вектор
нөл вектор
деп аталады да, былай белгiленедi:
 немесе
немесе
 ,
,
 . Нөл векторлардың бағыттары анықталмаған, модульдерi нөлге тең және олар өзара тең.
. Нөл векторлардың бағыттары анықталмаған, модульдерi нөлге тең және олар өзара тең.
 нөл векторы
нөл векторы
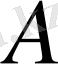 нүктесiнен өтетiн кез келген түзулердiң бойында жатады, сондықтан нөл вектор - кез келген вектормен коллинеар деп айтуға болады. Кез келген вектор өзiне-өзi коллинеар бола алады.
нүктесiнен өтетiн кез келген түзулердiң бойында жатады, сондықтан нөл вектор - кез келген вектормен коллинеар деп айтуға болады. Кез келген вектор өзiне-өзi коллинеар бола алады.
Егер
 мен
мен
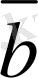 векторлары параллель және модулдерi тең, ал бағыттары қарама-қарсы болса, онда мұндай векторлар
қарама-қарсы
векторлар
деп аталады (4-сурет) .
векторлары параллель және модулдерi тең, ал бағыттары қарама-қарсы болса, онда мұндай векторлар
қарама-қарсы
векторлар
деп аталады (4-сурет) .
4-сурет
Қарама-қарсы векторлардың байланысын былай көрсетемiз
 .
.
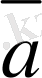 векторының қарама-қарсы векторын
векторының қарама-қарсы векторын
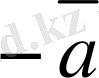 деп белгiлеуге болады. Егер
деп белгiлеуге болады. Егер
 мен
мен
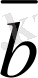 векторларының модулдерi ғана тең болса, онда бұл векторлардың өзара теңдiгi туралы ешқан-дай тұжырым айтуға болмай-ды, яғни олар жалпы жағдай-да тең немесе тең емес болуы да мүмкiн.
векторларының модулдерi ғана тең болса, онда бұл векторлардың өзара теңдiгi туралы ешқан-дай тұжырым айтуға болмай-ды, яғни олар жалпы жағдай-да тең немесе тең емес болуы да мүмкiн.
2. 2. Векторларды қосу
Берiлген
 ,
,
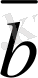 ,
,
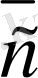 , . . . ,
, . . . ,
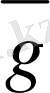 коллинеар емес векторларын былай орналастырайық:
коллинеар емес векторларын былай орналастырайық:
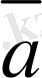 векторының соңғы нүктесi
векторының соңғы нүктесi
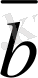 векторының бас нүктесiмен,
векторының бас нүктесiмен,
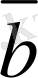 векторының соңғы нүктесi
векторының соңғы нүктесi
 векторының бас нүктесiмен үйлестiрейiк, ал қалғандарында осылай тiзбектеп орналастырайық.
векторының бас нүктесiмен үйлестiрейiк, ал қалғандарында осылай тiзбектеп орналастырайық.
Анықтама.
Берiлген
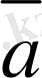 ,
,
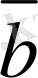 ,
,
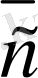 , . . . ,
, . . . ,
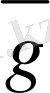 векторларының
қосындысы
деп бас нүктесi
векторларының
қосындысы
деп бас нүктесi
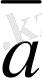 векторының бас нүктесiмен үйлесетiн, ал соңғы нүктесi
векторының бас нүктесiмен үйлесетiн, ал соңғы нүктесi
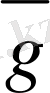 векторының соңғы нүктесiмен үйлесетiн
векторының соңғы нүктесiмен үйлесетiн
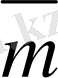 векторын айтамыз (5-сурет) .
векторын айтамыз (5-сурет) .
Осы векторлардың қосындысы былай белгiленедi:
+
+
+
+ . . . +
=
.
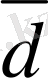
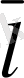
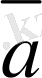
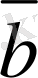
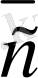
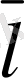
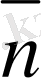
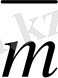
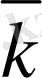
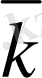
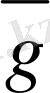
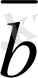
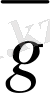
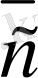
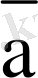
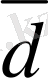
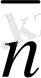
5-сурет
Жоғарыдағы анықтаманы пайдаланып, коллинеар емес
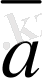 мен
мен
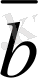 век-торларының қосындысын анықтайық. Ол үшiн
век-торларының қосындысын анықтайық. Ол үшiн
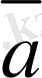 векторының соңғы нүкте-сiн
векторының соңғы нүкте-сiн
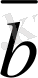 векторының бас нүктесiмен үйлестiрейiк, сонда
векторының бас нүктесiмен үйлестiрейiк, сонда
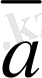 мен
мен
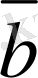 векторларының қосындысы
деп - бас нүктесi
векторларының қосындысы
деп - бас нүктесi
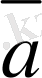 векторының бас нүктесiмен, ал соңғы нүктесi
векторының бас нүктесiмен, ал соңғы нүктесi
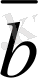 векторының соңғы нүктесiмен үйлесетiн
векторының соңғы нүктесiмен үйлесетiн
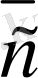 векторын айтады, яғни
векторын айтады, яғни
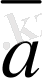 +
+
 =
=
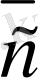 (6-сурет) .
(6-сурет) .
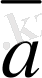 A
A
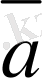 O
O
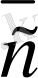
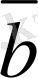
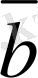
B
C
6-сурет
Берiлген
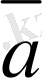 мен
мен
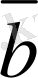 векторларының қосындысын табу үшiн
параллелограмм ережесiн
пайдаланып табуға да болады. Ол үшiн жа-зықтықтағы 0 нүктесiн берiлген
векторларының қосындысын табу үшiн
параллелограмм ережесiн
пайдаланып табуға да болады. Ол үшiн жа-зықтықтағы 0 нүктесiн берiлген
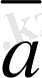 мен
мен
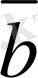 векторларының бас нүктесi етiп аламыз да, осы нүктеден
векторларының бас нүктесi етiп аламыз да, осы нүктеден
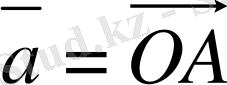 мен
мен
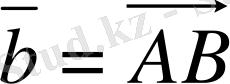 векторларын тұрғызамыз. Осы тұрғызылған векторлар арқылы
векторларын тұрғызамыз. Осы тұрғызылған векторлар арқылы
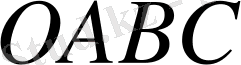 параллелограмын саламыз. Параллелограмның
параллелограмын саламыз. Параллелограмның
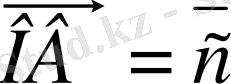 диагоналы, берiлген векторлардың қосындысы болады, яғни
диагоналы, берiлген векторлардың қосындысы болады, яғни
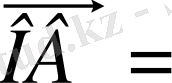
 +
+
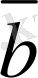 .
.
Жоғарыда берiлген анықтамадан, векторларды қосу амалына мына қасиеттер орындалады:
- - ауыстырымдылық заңы;
- - терiмдiлiк заңы;
- ;
- Кез келгенвекторына қарама-қарсывекторы табылып, теңдiгi орындалады.
2. 3. Векторлардың айырымы
Анықтама.
Берiлген
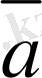 мен
мен
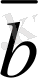 векторларының
айырымы
деп - үшiншi
векторларының
айырымы
деп - үшiншi
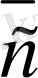 векторын айтамыз, егер
векторын айтамыз, егер
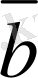 мен
мен
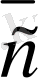 векторларының қосын-дысы
векторларының қосын-дысы
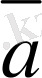 векторына тең болса
векторына тең болса
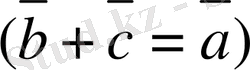 ол былай белгiленедi:
ол былай белгiленедi:
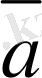 -
-
 =
=
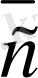 .
.
Осы анықтаманы пайдаланып, берiлген
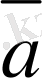 мен
мен
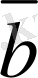 векторларының
векторларының
 -
-
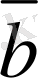 айырымын табайық. Ол үшiн
айырымын табайық. Ол үшiн
 мен
мен
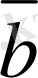 вектор-ларын ортақ бас О нүктесiмен үйлестiрелiк (7-сурет), яғни
вектор-ларын ортақ бас О нүктесiмен үйлестiрелiк (7-сурет), яғни
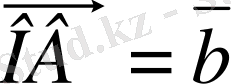 ,
,
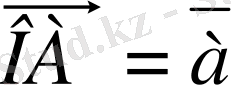 .
.
 -дан және жоғарыдағы анықтамадан мына теңдiктi аламыз:
-дан және жоғарыдағы анықтамадан мына теңдiктi аламыз:
 немесе
немесе
 .
.
Сонда,
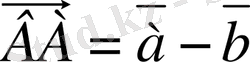 болады. Сонымен, берiлген
болады. Сонымен, берiлген
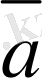 мен
мен
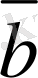 векторларының айырымын табу үшiн (7-сурет),
векторларының айырымын табу үшiн (7-сурет),

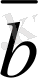

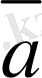

7-сурет
алдымен осы векторларды ортақ бас О нүктесiне үйлестiремiз де, бастапқы нүкте
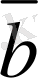 векторының соңғы нүктесiмен үйлесетiн, ал соңғы нүкте
векторының соңғы нүктесiмен үйлесетiн, ал соңғы нүкте
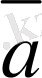 векторының соңғы нүктесiмен үйлесетiн
векторының соңғы нүктесiмен үйлесетiн
 векторын тұрғызамыз. Сонда, осы
векторын тұрғызамыз. Сонда, осы
 векторы
векторы
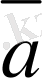 мен
мен
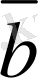 векторларының айырымы болады. Осы векторлардың айырымын қосу амалын пайдаланып та табуға болады. Ол үшiн
векторларының айырымы болады. Осы векторлардың айырымын қосу амалын пайдаланып та табуға болады. Ол үшiн
 мен
мен
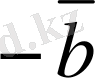 векторларының қосындысын анықтасақ жеткiлiктi,
векторларының қосындысын анықтасақ жеткiлiктi,
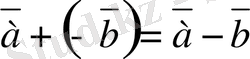 (8-сурет) .
(8-сурет) .
0
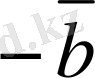
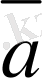
8-сурет
2. 1-теорема. Берiлген екi вектордың айырымы әрқашанда бар және ол тек бiреу ғана.
2. 4 Векторларды санға көбейту
Анықтама.
Берiлген
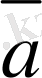 векторын скаляр
векторын скаляр
 санына көбейту
деп, мына үш шартты қанағаттандыратын
санына көбейту
деп, мына үш шартты қанағаттандыратын
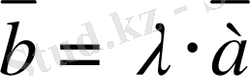 векторын айтамыз:
векторын айтамыз:
- ;
- . 3 мен. 3 векторлары коллинеар;
- Егер. 3 болса, онда. 3 мен. 3 векторларының бағыттары бiр бағыттас; егер. 3 болса, онда олардың бағыттары қарама-қарсы бағыттас.
Осы анықтамадан мынадай тұжырымдар аламыз:
егер
 немесе
немесе
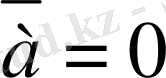 болса, онда
болса, онда
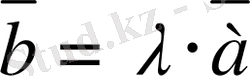 - нөл вектор;
- нөл вектор;
егер
 болса, онда
болса, онда
 . 3 мен
. 3 мен
 . 3 векторлары беттеседi;
. 3 векторлары беттеседi;
кез келген
 . 3 векторы үшiн
. 3 векторы үшiн
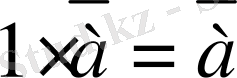 . 3 теңдiгi орындалады;
. 3 теңдiгi орындалады;
кез келген
 . 3 вектор мен
. 3 вектор мен
 . 3 саны үшiн тек бiр ғана
. 3 саны үшiн тек бiр ғана
 векторы анықталады.
векторы анықталады.
Векторларды скаляр санға көбейту амалына мына қасиеттер орындалады (
 скаляр шама) :
скаляр шама) :
- ;
- ;
- .
2. 5. Коллинеар және компланар векторлар
2. 2-теорема.
Берiлген
 . 3 мен
. 3 мен
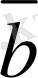 . 3 векторлары сызықты тәуелдi болу үшiн олардың өзара коллинеарлығы қажеттi, әрi жеткiлiктi.
. 3 векторлары сызықты тәуелдi болу үшiн олардың өзара коллинеарлығы қажеттi, әрi жеткiлiктi.
қажеттiлiгi.
Берiлген
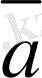 . 3 мен
. 3 мен
 . 3 векторлары сызықты тәуелдi деп ұйғаралық та, олардың коллинеар екендiгiн дәлелдейiк. Ұйғаруымыз бойынша
. 3 векторлары сызықты тәуелдi деп ұйғаралық та, олардың коллинеар екендiгiн дәлелдейiк. Ұйғаруымыз бойынша
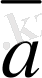 . 3 мен
. 3 мен
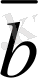 . 3 сызықты тәуелдi векторлар, сондықтан анықтама бойынша
. 3 сызықты тәуелдi векторлар, сондықтан анықтама бойынша
 . 3 мен
. 3 мен
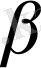 нақты сандары табылып,
нақты сандары табылып,
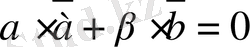 (2. 3)
(2. 3)
теңдiгi орындалады.
Ендi
 мен
мен
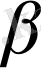 сандарының бiрiн, яғни
сандарының бiрiн, яғни
 болсын дейiк, олай болса, (2. 3) теңдiктен мына теңдiктi аламыз:
болсын дейiк, олай болса, (2. 3) теңдiктен мына теңдiктi аламыз:
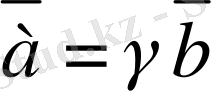 ,
,
мұндағы
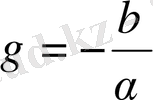 .
.
Соңғы теңдiктен және векторды скаляр санға көбейту анықтамасын еске түсiрсек, онда
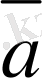 мен
мен
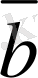 векторларының
коллинеар
екендiгi шығады.
векторларының
коллинеар
екендiгi шығады.
Жеткiлiктiлiгi.
Ендi
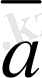 мен
мен
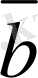 векторларын коллинеар деп үйғаралық та, олардың сызықты тәуелдi векторлар екендiгiн дәлелдейiк. Ол үшiн екi жағдайды қарастырамыз.
векторларын коллинеар деп үйғаралық та, олардың сызықты тәуелдi векторлар екендiгiн дәлелдейiк. Ол үшiн екi жағдайды қарастырамыз.
Бiрiншi жағдай. Берiлген векторлардың бiрi нөл вектор болсын делiк. Онда, бұл векторлардың сызықты тәуелдiлiгi бiрiншi қасиеттен алынады.
Екiншi жағдай.
Берiлген
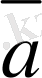 мен
мен
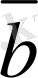 векторларының екеуi де нөл емес вектор делiк. Онда,
векторларының екеуi де нөл емес вектор делiк. Онда,
 . 3 нақты саны табылып, мына теңдiк орындалады:
. 3 нақты саны табылып, мына теңдiк орындалады:
 немесе
немесе
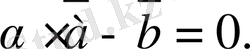 (2. 4)
(2. 4)
Соңғы теңдiкте, мынадай екi жағдай болуы мүмкiн
 . 3 немесе
. 3 немесе
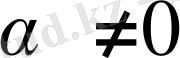 . 3. Екi жағдайда да
. 3. Екi жағдайда да
 болғандықтан, (2. 4) теңдiгi
болғандықтан, (2. 4) теңдiгi
 . 3 мен
. 3 мен
 . 3 векторларының сызықты тәуелдiлiгiн анықтайды. Теорема дәлелдендi.
. 3 векторларының сызықты тәуелдiлiгiн анықтайды. Теорема дәлелдендi.
Анықтама. Бiр жазықтықтың бойында жатқан немесе бiр жазықтыққа параллел болатын векторларды - компланар векторлар деймiз.
Осы анықтамадан, кез келген екi вектор - компланар болады.
2. 3-теорема.
Кез келген үш
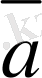 . 3,
. 3,
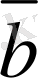 . 3,
. 3,
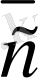 векторлар сызықты тәуелдi болу үшiн, олардың компланарлығы қажеттi, әрi жеткiлiктi.
векторлар сызықты тәуелдi болу үшiн, олардың компланарлығы қажеттi, әрi жеткiлiктi.
Осы теоремадан мынадай салдар аламыз.
Салдар.
Егер
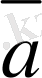 . 3,
. 3,
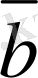 . 3,
. 3,
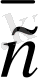 компланар емес векторлар болса, онда олар сызықты тәуелсiз.
компланар емес векторлар болса, онда олар сызықты тәуелсiз.
2. 6. Базис
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz