Туынды және дифференциалдық теңдеулер: өрнектерді ықшамдау мен жаратылыстану ғылымдарындағы модельдеу


Туындыны қолданып өрнекті ықшамдау
Туынды мектепте негізінен функцияларды зерттеуде қолданылады. Функцияны туынды арқылы зерттеу тақырыбынан басқа да есептерді туынды ұғымын қолданып шығаруға болады.
Туынды арқылы алгебралық және тригонометриялық теңдеулерді түрлендіруге, яғни өрнектерді көбейткіштерге жіктеуге болады.
Мысал 1: Мына өрнекті
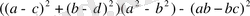 көбейткіштерге жіктейік.
көбейткіштерге жіктейік.
С-ны айнымалы деп алып өрнекті f(c) функциялдық деп алып туындыны табамыз.
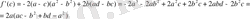
Сондықтан
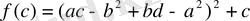
Мұнда c, a, b, d параметрлерімен берілген өрнек, бұдан
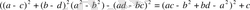 c=0 деп алып
c=0 деп алып
 онда
онда
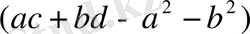 өрнекті алғашқы өрнкетің шешімі болып табылады.
өрнекті алғашқы өрнкетің шешімі болып табылады.
2.
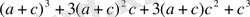
өрнегін көбейткіштерге жіктеп c-ны айнымалы деп алып, туындыны табамыз.
 Equation. 3 онда с=0 деп алсақ, с=0, онда
Equation. 3 онда с=0 деп алсақ, с=0, онда
 Equation. 3
Equation. 3
 өрнегі берілген функцияның шешімі болады.
өрнегі берілген функцияның шешімі болады.
3.
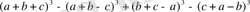
өрнекті f(a) деп белгілей отырып
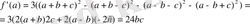 Equation. 3
Equation. 3
 Equation. 3
Equation. 3

Сонымен берілген өрнектің шешімі 24авс .
4. өрнекті ықшамдау.
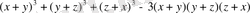
өрнекті f(x) белгілеп туындысын табайық.

Бұдан егер
х=0
деп алсақ
 онда өрнектің шешімі
онда өрнектің шешімі
 тең болады.
тең болады.
Дифференциалдық теңдеулер арқылы
пәнаралық байланыстарды жүзеге асыру
Дифференциалдық теңдеулер курсы студенттердің белгілі бір математикалық мәдени немесе олардың ғылыми, әсіресе математиканы оқыту практикалық және қолданбалы бағыттардың мәнін түсіну, сол сияқты математикалық модельдеудің әсерін меңгеру мен пәнаралық байланыстарды жүзеге асыру іскерлігі сияқты көзғарастарын қалыптастырады. Оның пәнаралық байланыстары жүзеге асыру жолдарын көрсетейік.
Дүниеге нақты процестердің ең қарапрйымы - бір қалыпты процестер. Бұл процестер тұрақты жылдамдық арқылы туындайды. Күрделілігі жағынан келесі процесс - ол үдеулері тұрақты жылдамдық арқылы туындайды. Күрделелігі жағынан келесі процесс - ол үдеулері тұрақты, жылдамдықтары бірқалыпты өзгеретін процестер. Осы екі жағдайда жылдамдық айнымалы шамалардың мәндерінен тәуелсіз. Алайда, көбінесе, шаманың өзгеру жылдамдығының мәні сол шаманың мәніне байланысты. Мысал, жинақ кассаларына саланатын ақша көп болған сайын, оның жылдық өнімі арта түседі. Сондықтан көп жағдайда t мезгілдері шаманың өзгеру жылдамдығымен осы шаманың дәл сол мезгілі ішіндегі мәні пропорционал деп қарастыруға болады. Осы айтылғандардан келесі түрде тұжырмдалатын математикалық есепке келеміз: t мезгілдегі у шаманың мәні у 0 -ге тең болса, онда t мезгілдегі у-тің мәнін табамыз.
Есептің шарты бойынша
 , ал
, ал
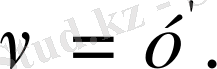 олай болса
олай болса
 дифференциалдық теңдеуін аламыз. Тікелей тексеру арқылы
дифференциалдық теңдеуін аламыз. Тікелей тексеру арқылы
 функцияның осы теңдеуді қанағаттандыратынын көз жеткізу қиын емес, яғни ол теңдеудің шешуі болып табылады және басқа шешу жоқ. Шынында, айталық
функцияның осы теңдеуді қанағаттандыратынын көз жеткізу қиын емес, яғни ол теңдеудің шешуі болып табылады және басқа шешу жоқ. Шынында, айталық
 болсын.
болсын.

Сөйтіп
 осыдан
осыдан
 яғни
яғни
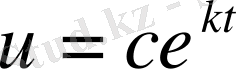
Сонымен
 функциясы да
функциясы да
 теңдеудің шешуі екен. Шарт бойынша
у=у
0
,
яғни
теңдеудің шешуі екен. Шарт бойынша
у=у
0
,
яғни
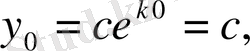 олай болса
олай болса
 Сөйтіп іздеп отырған мәніміз
Сөйтіп іздеп отырған мәніміз
 болады екен.
болады екен.
Осы қарастырған математикалық моделіміз көптеген физикавлық, химиялық, биологиялық т. б. процестерді айқындауға мүмкіндік береді.
Мысал. 1 Саны ашытуға қажет ферменттердің өсу жылдамдығы оның х санына пропорционал. Алғашқы бір сағатта ферменттердіңсаны екі есе өссе, үш сағаттан кейін ол қанша есе өседі?
Шешуі. Есептің шарты бойынша оның дифференциалдық теңдеуі
 болады. Мұндағы
к
-пропорционалдық коэффицент. Бұл теңдеудің шешуі
болады. Мұндағы
к
-пропорционалдық коэффицент. Бұл теңдеудің шешуі
 Пропорционалдық коэффиценттерін бастапқы шарт арқылы анықтаймыз. Яғни
t=1
болғанда
x=2a
болады. Олай болса
Пропорционалдық коэффиценттерін бастапқы шарт арқылы анықтаймыз. Яғни
t=1
болғанда
x=2a
болады. Олай болса
 немесе
е
к
=2
. Осы өрнекті теңдеуіне шешуіне қойып, қарастырып отырған процестің заңдылығын
немесе
е
к
=2
. Осы өрнекті теңдеуіне шешуіне қойып, қарастырып отырған процестің заңдылығын
 теңдеудегі түрінде аламыз. Осыдан, егер
t=3
болса, онда
x=8a,
яғни үш сағат өткеннен кейін ферменттердің саны 8есе өседіекен.
теңдеудегі түрінде аламыз. Осыдан, егер
t=3
болса, онда
x=8a,
яғни үш сағат өткеннен кейін ферменттердің саны 8есе өседіекен.
Мысал. 2 Металл пластинканы суыту үшін ол белгілі бір температурада суы бар үлкен ваннаның ішіне салынсын. Температураның өзгеру жылдамдығы денемен оны қоршаған ортаның температурасының айырымына процестің оның температурасына ешқандай әсер болмасын, сол сияқты салынған дененің температурасы барлық жерінде бірдей болсын деп жори отырып, дененің суу заңдылығын табалық.
Шешуі. Уақыты t, ал денемен ортаның температурасының айырымын
 арқылы белгілесек, онда суу заңдылығы
арқылы белгілесек, онда суу заңдылығы
 теңдеуімен өрнектеледі. Мұндағы
к
- материалға тәуелді тұрақты шама. Осы дифференциалдық теңдеуді шеше отырып
теңдеуімен өрнектеледі. Мұндағы
к
- материалға тәуелді тұрақты шама. Осы дифференциалдық теңдеуді шеше отырып
 заңдылығын аламыз.
заңдылығын аламыз.

Дифференциалдық теңдеуді биологиялық процестерде қолдану
Математиканың көптеген австрактілі теориялары мен негізгі принциптерінің жаратылыстану ғылымдарының маңызды мәселелерін шешуге қолдану жолдары математикалық бір ірі бөлігі - дифференциалдық теңдеулер арқылы жүзеге асады. Дифференциалдық теңдеулердің көмегімен жаратылыстану ғылымдарындағы ең негізгі проблеманың бірі өзімізді қоршап тұрған табиғат құбылыстарының кейбір жасырын сырының қалай ашылған, оның өмірде қалай пайдаланылатынын көрсетуге болады.
Соның бір мысалы дифференциалдық теңдеулерді популяцияны (мекендес өсіп-өну) санының қарапайым моделі ретінде көрсету жатады. Популяция саны - қоршаған ортаны қорғаудың, яғни биоэкологияның ең маңызды мәселесі болып табылады. Популяцияның математикалық моделін құру биологиялық түрдің сан жағынан өсуінің жылдамдығын анықтайтын есеп ретінде қарастырылады.
Егер популяцияны жекеленген (оңашаланған), қоректік қоры шектеусіз, өсім басы ересек особьтардың санына пропорционал деп есептесек, онда популяция санының динамикасы мынандай қарапайым дифференциалдық теңдеумен анықталады:
 (1)
(1)
Мұндағы x=x(t) - кез-келген t уақыт моментіндегі популяция саны. Алғашқы t=t 0 моментінде популяция саны x=x 0 болсын. (1) теңдеу бірінші ретті сызықты біртекті дифференциалдық теңдеу болғандықтан оның шешімі мына түрде болады:
 (2)
(2)
(2) теңдеу популяцияның өсуінің экспоненциалдық формуласы деп аталады.
Пропорционалдық коэффицент y-ның қабылдайтын мәнінің әр түрлі жағдайына байланысты популяция санының динамикасы да әр түрлі болады. Егер y>0 болса, онда уақыт өткен сайын популяция өседі; егер y=0 болса, онда ол бастапқы x=x 0 қалпында қалады; егер y<0 болса, онда уақыт өткен сайын популяция нольге дейін кемиді, яғни қарастырылып отырған түр жойылып кетеді. Осы үш жағдай 1-суретте көрсетілген.
Популяция динамикасының дәл сипаттамасын 1845 жылы алынған Ферхюльст-Перл теңдеуі береді. Ол теңдеуде популяцияның «Өзін-өзі уландыру» немесе «популяциядағы түр ішіндегі тіршілік үшін күрес» факторы ескерілген. Популяцияның өсу жылдамдығын тежейтін бұл фактор көптеген себептермен түсіндіріледі: мысалы, мекен ететін жер мен қорек үшін күрес, тығыз орналасуға байланысты инфекцияның таралуы т. с. с.
Осы факторлардың әсерін ескере отырып, популяцияның, ∆x өсімшесін есептегенде yx∆t шамасынан қандай да бір h(x, ∆t) шамасын шегеруіміз керек: ∆x=yx∆t-h(x, ∆t)
h(x, ∆t) функциясы көптеген популяция үшін мынандай көбейтінді түрінде болады:
h(x, ∆t) =δx 2 ∆t (3)
 Мұндағы,
Мұндағы,
 - өзін-өзі улау (немесе популяциядағы ішкі күрес) коэффиценті. (3) теңдеудегі х
2
функциясының алынуы былайша негізделеді. h(x, ∆t) шамасы түр ішіндегі тіршілік үшін күрестен популяция санының өсу жылдамдығының төмендеуін көрсетеді. Особьтар арасындағы кездесу неғұрлым көп болса конкуренция соғұрлым көп болады, ал олардың түр ішіндегі кездесу саны x*x=x
2
- өзін-өзі улау (немесе популяциядағы ішкі күрес) коэффиценті. (3) теңдеудегі х
2
функциясының алынуы былайша негізделеді. h(x, ∆t) шамасы түр ішіндегі тіршілік үшін күрестен популяция санының өсу жылдамдығының төмендеуін көрсетеді. Особьтар арасындағы кездесу неғұрлым көп болса конкуренция соғұрлым көп болады, ал олардың түр ішіндегі кездесу саны x*x=x
2
Сонымен,
 (4)
(4)
(4) теңдеуді мүшелеп ∆t-ға бөлеміз:
 (5)
(5)
∆t→0-да шекке көшсек, мынандай дифференциалдық теңдеу аламыз:
 (5)
(5)
Бұл Ферхюльс-Перл теңдеуі деп аталады. (5) теңдеуді көбінесе мына түрде жазады.
 немесе
немесе

Егер
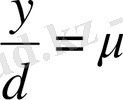 белгілеуін енгізсек, (5) теңдеуі былайша жазылады:
белгілеуін енгізсек, (5) теңдеуі былайша жазылады:
 (6)
(6)
Егер
 болса, уақыттың барлық моментінде
t>t
0
болады. Шынында да, x(t) - дифференциалданатын функция. (6) теңдеуден
болса, уақыттың барлық моментінде
t>t
0
болады. Шынында да, x(t) - дифференциалданатын функция. (6) теңдеуден
 болғанда ғана
болғанда ғана
 туындысының оң болатынын көреміз, яғни
x(t)
функциясы өседі. Бұдан x(t) функциясы
туындысының оң болатынын көреміз, яғни
x(t)
функциясы өседі. Бұдан x(t) функциясы
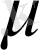 -ге мәнді өспелі бола отырып,
-ге мәнді өспелі бола отырып,
 түзуін қиғанда немесе оған жанасқанда қабылдайтын болады.
түзуін қиғанда немесе оған жанасқанда қабылдайтын болады.
Бірінші жағдайда (2-сурет) қиылысу нүктесінің оң жағында
 және
және
 . Бұл арақатынастар (6) теңдеуге қайшы келеді. Екінші жағдайда (3-сурет) жанасу нүктесінің оң жағында
. Бұл арақатынастар (6) теңдеуге қайшы келеді. Екінші жағдайда (3-сурет) жанасу нүктесінің оң жағында
 және
және
 . Бұл да (6) теңдеуге қайшы келеді.
. Бұл да (6) теңдеуге қайшы келеді.
Сонымен,
 болғанда
x(t)
функциясы
болғанда
x(t)
функциясы
 -ге тең мәнді қабылдайды.
-ге тең мәнді қабылдайды.
х х
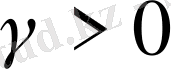



х 0 х 0

t t 0 t
1-сурет 2-сурет
x

x 0
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz