Дифференциалдық теңдеулерді шешу алгоритмін құру және сол теңдеулерді Matlab жүйесінде көрсету

КІРІСПЕ 4
1 Негізгі бөлім 6
1.1 Математикада диффиренциалдық теңдеулерді шешудің
әдістері: Эйлер, Рунге.Кутт және Адамс 7
1.2 Қолмен есептеудегі мысалдар 13
1.3 Matlab көмегімен есептерді шығару әдістері 15
1.4 Matlab.та есептеулерді жүргізу 22
ҚОРЫТЫНДЫ 34
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ 35

Көптеген инженерлік есептеулер әртүрлі интерпретаторлар көмегімен шығарылады. Олардың түрлері және мүмкіндіктері бар. Солардың көмегімен инженерлер және программистер күрделі есепеулерді бір минуттың ішінде шығару мүмкіндіктері бар. Осы интерпретаторлардың ішінде қазіргі кезде көптеген жерлерде қолданылатын Matlab жүйесі де бар.
Matlab жүйесінің операциялық жүйесі – бұл осы жүйенің сыртқы дүниемен байланысты қолдайтын күрделі интерфейс. Себебі MatLab көптеген математикалық жүйелерге қарағанда ашық жүйе болып табылады, яғни бұл MatLab-тың барлық процедуралары мен функциялары тек қана пайдалануға ғана емес, сонымен қатар коррекция мен модификация үшін де жарамды. MatLab – қолданушының өзі жазған программа мен процедуралар арқасында өз қалауынша кеңейтілетін жүйе. Оны керекті есептер класына оңай ыңғайластыруға болады.
Зерттеуге көп қолдану және мықты ғылыми калькулятор режимінде жұмыс атқаратын барлық жүйенің есептеу мүмкіндіктерін көру мақсатында өзіңнің бөлек программаңды жазуға өте ыңғайлы. Бұл MatLab-ты ғылыми есептік зерттеулерді жүргізуде теңдесі жоқ жүйе екенін көрсетеді.
Программа дамытуда программалаудың түрлі әмбебап тілдері қолданды. 90-жылдың басында олардың орнын компьютерлік математиканың арнаулы жүйелері басты. Олардың қатарында MATLAB-тың өзіндік орны бар. Ол арнаулы материялық программалау модулінен бастап компьютерлік математиканың әмбебап жүйелеріне дейінгі даму кезеңінен өтті. MATLAB ең күрделі математикалық есептеулерді әмбебап материялық түрде келтірілген мәліметтерді қолдана отырып шешуге арналған.

Самарский А.А. Численные методы/-М.:Наука, 1989.
Лазарев Ю. MatLab 5.0/К.:Ирина, 2000.
www.matlab.com
Бахвалов Н.С. Численные методы. - М.: Наука, 1989
Демидович Б.П. Численные методы анализа. – М.: Наука, 1989
Турчак Л.И. Основы численных методов: Учеб. Пособие. – М.: Наука.

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 26 бет
Таңдаулыға:

МАЗМҰНЫ

Кіріспе 4
1. Негізгі бөлім 6
1.1 Математикада диффиренциалдық теңдеулерді шешудің
әдістері: Эйлер, Рунге-Кутт және Адамс 7
1.2 Қолмен есептеудегі мысалдар 13
1.3 Matlab көмегімен есептерді шығару әдістері 15
1.4 Matlab-та есептеулерді жүргізу 22
Қорытынды 34
Қолданылған Әдебиеттер тізімі 35

КІРІСПЕ

Көптеген инженерлік есептеулер әртүрлі интерпретаторлар көмегімен
шығарылады. Олардың түрлері және мүмкіндіктері бар. Солардың көмегімен
инженерлер және программистер күрделі есепеулерді бір минуттың ішінде
шығару мүмкіндіктері бар. Осы интерпретаторлардың ішінде қазіргі кезде
көптеген жерлерде қолданылатын Matlab жүйесі де бар.
Matlab жүйесінің операциялық жүйесі – бұл осы жүйенің сыртқы
дүниемен байланысты қолдайтын күрделі интерфейс. Себебі MatLab көптеген
математикалық жүйелерге қарағанда ашық жүйе болып табылады, яғни бұл MatLab-
тың барлық процедуралары мен функциялары тек қана пайдалануға ғана емес,
сонымен қатар коррекция мен модификация үшін де жарамды. MatLab –
қолданушының өзі жазған программа мен процедуралар арқасында өз қалауынша
кеңейтілетін жүйе. Оны керекті есептер класына оңай ыңғайластыруға болады.
Зерттеуге көп қолдану және мықты ғылыми калькулятор режимінде жұмыс
атқаратын барлық жүйенің есептеу мүмкіндіктерін көру мақсатында өзіңнің
бөлек программаңды жазуға өте ыңғайлы. Бұл MatLab-ты ғылыми есептік
зерттеулерді жүргізуде теңдесі жоқ жүйе екенін көрсетеді.
Программа дамытуда программалаудың түрлі әмбебап тілдері қолданды. 90-
жылдың басында олардың орнын компьютерлік математиканың арнаулы жүйелері
басты. Олардың қатарында MATLAB-тың өзіндік орны бар. Ол арнаулы материялық
программалау модулінен бастап компьютерлік математиканың әмбебап жүйелеріне
дейінгі даму кезеңінен өтті. MATLAB ең күрделі математикалық есептеулерді
әмбебап материялық түрде келтірілген мәліметтерді қолдана отырып шешуге
арналған.
MATLAB жүйесі әскери өндірістік кешенде, агрокосмостық салада
стандартты пакеттер мен қолданбалы программалардың көп мәліметтері мен
техникалық есептеулерге арналған жоғары деңгейдегі программалау тілі болып
табылады.
Курстық жұмыстың негізгі мақсаты – дифференциалдық теңдеулерді шешу
алгоритмін құру және сол теңдеулерді Matlab жүйесінде көрсету.

Негізгі бөлім

Бір немесе бірнеше бастапқы функцияның у=у(х) туындысынан тұратын
теңдеулерді кәдімгі дифференциалды теңдеулер деп айтады. Оларды мына түрде
жазуға болады

F(x, y,y` ,...y(n))=0 (1)

мұндағы х – тәуелсіз айнымалы.
Дифференциалды теңдеудің реті деп (1) теңдеуге кіретін туындың ең
жоғарғы ретін айтамыз.
Сызықты дифференциалды теңдеу деп ізделінетін функцияға және оның
туындысына қатысты сызықты болатын теңдеуді айтады.
у=(x) функциясын (1) дифференциалды теңдеудің жауабы болады, егер
берілген теңдеуге у=(x) функцияны қойғаннан кейін бұл теңдеуде тепе-
теңдік орындалса.
n-ші ретті кәдімгі дифференциалды теңдеудің жалпы шешімі n еркін
тұрақтылар С1, С2 ,..., Сn құрайды. Яғни теңдеудің жалпы шешімінің түрі
мынадай

у=(х, С1, С2 ,..., Сn ) (2)

Егер еркін тұрақтыларға анықталған мәндер берілетін болса, жалпы
теңдеуден дифференциалды теңдеудің дербес шешімі шығады. Бірінші ретті
теңдеудің жалпы шешімі бір еркін тұрақтыға тәуелді.

у=(x, С) (3)

Егер тұрақтыға анықталған мән С= С0 берілетін болса, онда дербес
шешімді аламыз.

у=(х, С0) (4)

Дифференциалды теңдеудің шешімін табу үшін, берілген қосымша
шарттарына байланысты есеп екі әртүрлі түрі бар: Кошидың есебі және шеткі
есеп.
Егер бұл шарттар бір нүктеде берілсе, онда мұндай есеп Коши есебі деп
аталады. Кошидың есебінде берілген қосымша шарттар бастапқы шарттар, ал
х=х0 нүктесі бастапқы нүкте деп аталады.

Мысалы:

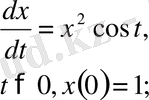
1.1 Математикада диффиренциалдық теңдеулерді шешудің әдістері

Кәдімгі дифференциалды теңдеудің шешу әдістерін келесі топтарға бөлуге
болады: графикалық, аналитикалық, жуықталған және сандық. Қазіргі уақытта
дифференциалды теңдеуімен берілетін ғылыми техникалық есептерді зерттеу
кезінде дифференциалды теңдеуді шешудің сандық әдістері негізгі құрал болып
саналады. Сонымен қатар бұл әдістер тез жұмыс істейтін, жедел жадысының
үлкен көлемі бар ЭВМ-мен бірге қолданғанда өте тиімді болады..

Эйлер әдісі

Дифференциалды теңдеулер үшін Коши есебін шешудің қарапайым сандық
әдісі – Эйлердің әдісі. Ол у(х) бастапқы функцияның х=хi (i=0.1,...,)
буындардың айналасында Тейлор қатарына жіктелуіне негізделген. Мұнда екінші
немесе одан да жоғары ретті туындылары бар барлық мүшелер лақтырылады. Бұл
жіктеуді мына түрде жазамыз

у(хi +xi)=y(x1)xi+0(xi2) (5)

Сонымен қатар 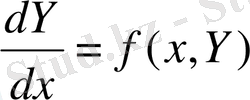теңдеуді қолдана отырып

У(хi)=f(xi, y(xi))-f(xi, yi) (6)

Қарапайымдылық үшін буындарды тұрақты деп санаймыз, яғни хi=xi+1-
xi=h=const (i=0.1...). Енгізілген көрсетулерді ескере отырып және 0(h2)
ретті мүшелерін ескермей (5) теңділіктен мынаны аламыз.

yi+1 =yi+hf(xi, yi), i=0,1... , (7)

i=0 деп, (6) арақатынасы көмегімен торлы функцияның у1 мәнін х=х1
мәнінде табамыз:

у=у0+hf(x0,у0) ()

Мұндағы сұранатын у0 мәні бастапқы шарттар, яғни у0=У(х0)=У0 . Тура
осылай торлы функцияның мәндері басқа да буындарда табылуы мүмкін.

у2 =y1+hf(x1, y1),
... ... ... ... ... ... ... .. (8)
уn =yn-1+hf(xn-1, yn-1)

Құрылған алгоритм Эйлер әдісі деп аталады.
Эйлердың әдісінің қателігі мынаған әкеліп соғады, әрбір қадам сайын
шешім басқа интегралдың қисыққа өтіп кете береді. Эйлердің әдісінің
қателігі туралы сұрағын нақтырақ қарастырайық. еi қателігі xi нүктесінде
торлы функция уi мәні мен бастапқы функция у(х1) нақты мәні арасындағы
айырмасына тең: еi=yi-У(xi). Бұл қателік екі бөліктен тұрады: еi=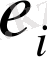+ei .
ei=e–ң құрайтыны алғашқы мәнінің қателігі e0=y0-y(x0) анықталады. Әдетте,
бастапқы мәні тура беріледі, яғни у0=у(х0) және онда еi=0. еi қателігі
Тейлор қатарына жіктеуде лақтырылған мүшелеріне байланысты. Әрбір қадамда
бұл қателік 0(h2) ретті. Өйткені (5)-де осы ретті мүшелер лақтырылған.
хn нүктесінде шешімді тапқан кезде, х0 нүктесінен L соңғы
арақашықтықта жататын қателік қосылады. Қосылған қателік шамасымен n0(h2)-
ке тең болады. Егере h=Ln екенін ескерсек, онда қосылған қателік үшін
мынадай өрнек аламыз:

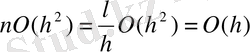(9)

Модификацияланған Эйлер әдісі

Эйлер әдісінің тағы бір схемасын берейік. f(x, У) теңдеудің оң жақ
бөлігінің (6) схемасындағы мәнін f(xi ,yi) арасында f(xi+1 ,yi+1)
арифметикалық орта мәніне тең етіп аламыз, яғни (6) айырмалар схемалардың
орнына

уi+1=yi+h2[f(xi,yi)+f(xi+1-yi+1)], i=0.1...,
(10)

алынған схема айқын емес, себебі ізделінетін Yi+1 мәні ара қатнастың
екі жағына да кіреді.

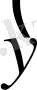i+1=yi+hf(xi,yi) (11)

жаңа мәнді 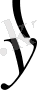i+1 мына 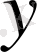i+1 орнына (10) оң жағына қоямыз және
шешуші мәнді табамыз.

yi+1=yi+h2[f(xi,yi)+f(xi+1,yi+1)] (12)

(11) алгоритмі (12) – ді бір арақатынас ретінде жазуға болады.

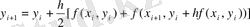(121)
i=0,1,...

Осы рекурректтік арақатнастар жаңа әртүрлік схеманы баяндайды. Бұл
Эйлердің әдісінің модификациясы болып келеді. Сөйтіп, Эйлердің
модификацияланған әдісі немесе Эйлер-Коши әдісі деп аталады.
Тейлор қатарына жіктеуді пайдалана отырып, осы әдіс екінші ретті
дәлдікті беретінін көрсетуге болады. Кошидың есебіне шығаруға қолданылуы
қателік мәнін 0(h2) көлеміне дейін кішірейтеді.
Модификацияланған Эйлер әдісін басқа түрдеде табуға болады. Функцияны
Тейлор қатарына жіктеуді қолданып, бұл жіктеуді мына түрде жазамыз:

уi+1=yi+hyi +h22yi+o(h3) (13)

Бұл схемада h2 мүшесі сақталуы керек. Бұл үшін екінші туындыны соңғы
айырымдық қатнастар көмегімен аппроксимациялаймыз:

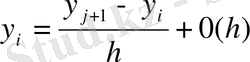(14)

осы арақатынасты (13) теңдеуіне қоямыз:

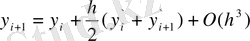
Туындық мәндерімен ауыстыра отырып

уi=f(xi,yi)Yi+1 =f(xi+1yi+1) (15)

Мұнда 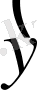i+1 (8) формуладан Эйлер әдісімен табылған,
модификацияланған Эйлер әдісінің айырымдық схемасына (12) қайта келеміз.
Мұндай (12) формуласын шығару әдістің қателігін бағалауға мүмкіндік берді.
(14) сәйкес әрбір қадамдағы (локальды) қателік h3 ретті, ал қателік
қосындысы - h2 ретті.
Эйлердің модификацияланған әдісі көмегімен i+1 ,Yi+1 мәндерін
салыстыру арқылы дәл шешуді бақылауға болады және осының негізінде әр
буында h қадамының мәнін таңдап алуға болады. Нақты айтқанда егер де
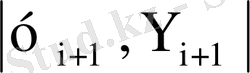мәні есептеу қателіктерімен салыстырмалы болса, онда қадамды үлкейтеміз,
әйтпесе бұл айырмашылық өте үлкен (мысалы, 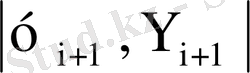0,01 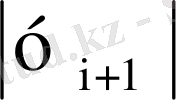) болса, онда h
мәнін азайту керек.

Рунге-Кутт әдісі

Басқа да нақты бір қадамдық әдістер бар. Соның ішінде көп тарағаны
Рунге-Кутт әдісі. Бұның негізінде әртүрлі реттік дәлдіктегі әртүрлілік
схемалар құрастыралуы мүмкін.
Рунге-Кутт схемасының төртінші реттігін келтірейік. Бұл әдістің
алгоритмін мына түрде жазайық:

уi+1=yi+h6(к0 +2к1 +2к2+к3) i=0,1,...
(16)

K0=f(xi,yi),
K1 =f(xi h2, yi +K02) (17)
K2=f(xi,h2,yi+ K12),
K3 =f(xi+ hi, yi +K2)

Сөйтіп, Ренге-Кутт әдісі әрбір қадамда f(x,y) теңдеудің оң жағын төрт
еселік есептеуді қажет етеді.
Эйлер әдісі (8) және оның модификацияланған нұсқауы (121) Рунге-Кутт
әдісінің бірінші және екінші ретті әдістері сияқты қарастырылуы мүмкін.
Рунге-Кутт әдісі (17) көп есептеуді қажет етеді, дегенмен бұл жоғары
дәлдікті береді. Бұл үлкен қадамды есептеуді жүргізуге мүмкіндік береді.
Басқа сөзбен айтқанда, Эйлер әдісінде бірдей дәлдікті нәтижелерін алу үшін,
әлде қайта аз қадам сұрайды.

Адамс әдісі

Рунге-Кутт әдісіне қарағанда кең тараған, көп қадамды әдістердің
әулеті болып Адамс әдісі саналады. Соның ішіндегі ең қарапайым к=1 болғанда
алынатын мән, Эйлердің алғашқы әдісі бірінші ретті дәлдікті
қарастырылғанмен сәйкес келеді. Іс жүзіндегі есептерлерде жиі кездерде
Адамс әдісінің нұсқауы пайдаланады, ол төртінші реттік дәлдікті беретін
және де әрбір қадамда алғашқы есептелген төрт нәтижелерді пайдаланады.
Осыны Адамс әдісі деп атайды. Бірінен кейін бірі орналасқан төрт буын
мәндері уі-3, уі-2, уі-1, уі табылсын. Сонымен қатар алдында есептелген оң
жағының мәндері 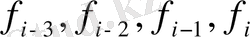бар болсын. Интерполяциялық көпмүшелік Р3 (х) ретінде
Ньютонның көпмүшелігін алуға болады. Тұрақты h қадамда соңғы айырмалар xi
буының оң жағы мынадай түрде болады:

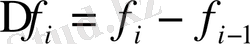
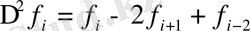(18)

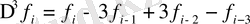
онда Адамс әдісінің 4-ші реттік әртүрлілік схемасы мына түрде
жазылады:
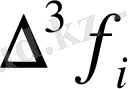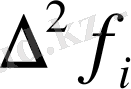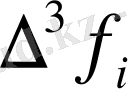уi+1=yi+hfi +h22 +5h312 +3h48 (19)

Адамс әдісін Рунге-Кутт әдісімен осындай дәлдікпен пен салыстыра
отырып, оның экономдылы екенін анықтаймыз. Себебі ол тек бір ғана мәннің
әрбір қадамдағы оң жағын есептеп шығаруын талап етеді. (Рунге –Кутт әдісі
төрт рет), бірақ Адамс әдісінің кемшілігі, ол белгілі бір ғана у0 мәнімен
есептеуді бастау мүмкін емес. у1, у2, у3 мәндері у3 есептеп шығару үшін
керек және оны басқа әдіспен алу қажет. Осының нәтижесінде әдіс алгоритмі
қиындай түседі. Одан басқа Адамс әдісінде h қадамын өзгертуге болмайды.
Нәтиже дәлдігін жоғарлату. Сандық есептеудің дәлдігін әртүрлі
жолдармен жоғарлатуға болады. Мысалға оны әртүрлілік схемалардың жоғарғы
ретті дәлдігін пайдалана отырып табуға болады. Бірақ мұндай схемалар тек
қана коэффиценттері тұрақты теңдеулерге құру ыңғайлы, ал егер коэффиценттер
айнымалылар болса, онда жоғарға ретті схемалар қиындыққа әкеп соғады.
h қадамының мәнін азайту арқылы да дәлдікті жоғарлатуға болады. Бірақ
бұл әдіс те үнемді емес.
Іс жүзінде сандық есептеудің дәлдігін жоғарлатып, машина уақытын
ұлғайтпай-ақ Рунге әдісі қолданылады. Оның мәні, бір айырымды схема
бойынша әртүрлі қадамдармен қайтадан жүргізіледі.
Рунге әдісімен сәйкес торлы функцияның торлы буындарында h қадамымен
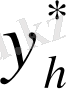нақты мәні мына формула бойынша есептеледі:

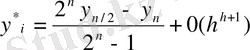(20)

Бұл есептеудің дәлдік реті k+1-ге тең.
Сөйтіп екі торда шешілетін есептер бір реттік нәтиженің дәлдігін
жоғарлатуға ықпал етеді. Эйлердің бірінші реттік дәлдігінің схемасына
арналған (К=1) Рунге формуласы мына түрде болады:

y* n=2yh2-yn+0(h2) (21)
1.2 Қолмен есептеудегі мысалдары

Мысал 1. Коши есебін шығар

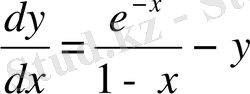
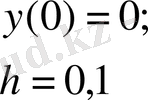
Негізгі әдістермен жуықталған мәндерін есептеп, 1-кестеге жаздым.

1-кесте
уі Эйлер әдісі Модификацияланған ЭйлерРунге-КутАдамс Нақты
әдісі т әдісі әдісі шешімі
0 0 0 0 0 0
1 0 0 0,0626 0,0626 0,0626
2 0,1005 0,0964 0,1221 0,1221 0,1221
3 0,1928 0,1947 0,1796 0,1796 0,1796
4 0,2793 0,2797 0,2673 0,2673 0,2673
5 0,3631 0,3641 0,3521 0,3521 0,3521
6 0,4481 0,4527 0,4383 0,4383 0,4383
7 0,5405 0,5542 0,5321 0,5321 0,5321
8 0,6520 0,6884 0,6454 0,6454 0,6454
9 0,8115 - 0,8081 0,8081 0,8081
10 1,1369 - 1,1424 1,1424 1,1424

Мысал 2. Коши есебін шығар

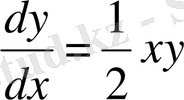
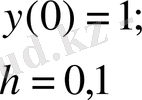
Бұл есепті жоғарыдағы әдістермен шығарып, 2-кестеге жаздым.

2-кесте
уі Эйлер әдісі Модификацияланған ЭйлерРунге-КутАдамс Нақты
әдісі т әдісі әдісі шешімі
0 1,0000 1,0000 1,0000 - 1,0000
1 1,0000 1,0025 1,0025 - 1,0025
2 1,0050 1,0100 1,0100 - 1,0100
3 1,0151 1,0227 1,0227 - 1,0227
4 1,0303 1,0408 1,0408 1,0408 1,0408
5 1,0509 1,0645 1,0645 1,0645 1,0645
6 1,0772 1,0942 1,0942 1,0942 1,0942
7 1,1095 1,1303 1,1303 1,1303 1,1303
8 1,1487 1,1735 1,1735 1,1735 1,1735
9 1,1946 1,2244 1,2244 1,2244 1,2244
10 1,2484 1,2839 1,2840 1,2840 1,2840

1.3 Matlab көмегімен есепті шығару әдістері

Көптеген жүйелердің және динамикадағы құрылыстардың жұмыс тәртібінің
анализін, сонымен бірге тербеліс теориясына және серпінді қабықтардың мінез-
құлқы деген тақырыптарға байланысты көптеген есептер кәдімгі
дифференциалдық теңдеулердің жүйесін шешу тақырыбына арналған. Оларды Коши
формадағы бірінші ретті дифференциалдық теңдеулерден құралған жүйе түрінде
береді:

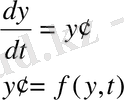
Шекті шарттар y(t0 tend, p)=b, мұндағы tend, t0 - интервалдың бастапқы және
соңғы нүктелері. Дифференциалдық теңдеулердің шешімдері уақыттық ауданда
ізделінсе де, мұндғы t параметрі уақытты білдірмейді. B векторы бастапқы
және соңғы шарттарын белгілейді.
Төменде кәдімгі дифференциалдық теңдеулерді шешуге арналған сандық әдістер
баяндалған, сонымен бірге дифференциалдық теңдеулердің жүйесін шешу үшін
көмекші функциялар қарастырылған.

жәй дифференциалдық теңдеулерді шығару

Matlab-тағы кәдімгі дифференциалдық теңдеулердің жүйесін шешу үшін
әртүрлі әдістер көрсетілген. Олар төменде көрсетілген:

• ode45 – Рунге-Куттың 4-ші және 5-ші ретті бірқадамды әдісі. Бұл
шешудің бастапқы сынауға арналған классикалық әдіс. Көптеген жағдайда
ол жақсы нәтиже береді.
• оde23 - Рунге-Куттың 2-ші және 4-ші ретті бірқадамды әдісі. Бұл әдісті
пайдалана отырып, дифференциалдық теңдеулерді шешудегі жылдамдығын
күшейтетін мүмкіндік пайда болады.
• оde113 – Адамс – Башфорт – Мултондарының айнымалы тізбегіндегі
көпқадамды әдісі. Бұл шешімнің жоғары нақтылығын бере алатын,
адаптерленген әдіс.
• ode23tb – Рунге – Куттың айқын емес әдісі, бұл әдіс екінші ретті
дифференциалдаудың кері формулаларын қолданады. Нәтиженің төмен
нақтылығына қарамасақ, бұл әдіс ode15s әдісінен эффектілі болады.
• ode15s – айнымалы тізбектің көпқадамды әдіс (1-ден 5-ке дейін, келісім
бойынша 5). Бұл әдіс сандық дифференциалдаудың формулаларын қолданады.
Бұл әдісті ode45 әдісі дұрыс шешімін бермесе қолдануға болады.
• оde23s – Розенброктың екінші ретті модификацияланған формуласын
қолданатын бірқадамды әдіс. Дифференциалдық теңдеулердің жүйесін
шешкендегі тез жылдамдықпен, бірақ төмен нақтылы шешімін қайтарады.
• оde23t – интерполяциядағы трапеция әдісі. Бұл әдіс гармоникалық шығыс
сигналымен тербелісті жүйелерін баяндайтын есептерді шешкенде нақты
да, жақсы нәтиже бере алады.
• bvp4c - y' =f(t,y), F(y(a), y(b), p)=0 (шекті есеп) типті шекті мәнді
дифференциалдық теңдеулер жүйесін шештін функция.
• Pdepe – жеке туындыларындағы параболалық ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.