Симплекс әдісімен параметрлік сызықты программалауды шешу және кестелік итерациялар


КІРІСПЕ
Симплекс әдісі . Бұл әдістің мағынасы мынада әуелі 2, 3 шарттарды қанағаттандыратын қандай да бір шешімді табамыз. Одан кейін белгілі тиімділік критериді пайдаланып, берілген есептің тиімді шешімін табамыз. Басқаша айтқанда есеп итерациялық әдіспен шешіледі. Яғни бір итерациядан 2-ші итерацияға көшкенде функцияның мәні кішірейе береді. Нәтижесінде есептің тиімді шешімі алынады. Шешімнің тиімділігі симплекс кесте арқылы тексеріледі.
Жүйелер теориясы әдістері-халық шаруашылығын тиімді басқару қажеттілігінен туған түрлі экономикалық, инженерлік есептерді шешуге бейімделген курс.
Әдетте экономикалық есептер қандай да болмасын кейбір өнімдерді, шикізаттарды үлестірумен байланысты болып келеді. Өнімдерді түрлі әдістермен бөлуге болады. Әдістер бір-бірінен тиімділігімен ажыратылады. Сондықтан экономикалық есептердің көп шешімдерінің ішінен жақсысын таңдау проблемалары туады. Үлестірудің ең жақсы варианты- тиімді аталады.
Осы сияқты есептер халық шаруашылығының әр саласында көптеп кездеседі. Химиялық өндіріс қалдықтарын тиімді пайдалану, өндіріс материалдарын тиімді шешу, кадрлары дайындау мен оларды орналастырудың тиімді жоспары және т. б.
Экономикалық есептерді экстремум анықтайтын математикалық есептермен байланыстыруға болады. Математикалық есептің шешімі- экономикалық есептің шешімі болады. 1Қоғамдағы экономикалық процестердің математикалық аппарат (теңдеулер, теңсіздіктер) арқылы сипатталуы-экономика-математикалық модель деп аталады. Экономикалық процестерді сипаттайтын математикалық есептердің шешіміне талдау арқылы біз экономикалық жүйені зерттейміз.
Есептің шарттарын өзгерте отырып, экономикалық жүйенің түрлі шешімдерін алып, олардың ішінен ең пайдалысын таңдаймыз.
Экстременальды есептер мен оның шығару әдістері қолданбалы математиканың “математикалық программалау” деп аталатын саласында қарастырылады.
1 Сызықты программалау есебін сиплекс әдісімен шешу.
Сызықты программалау есебінің тиімді шешімі шешімдер көп жағынының бұрыштық нүктелерімен, яғни әр қайсысы А
 …А
…А
- Тірек жоспарлар құру: симплексті программалау есебі берілсін.
Z = C
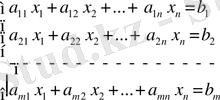 (2)
(2)
Табу керек ең кіші ең үлкен мәнін.
Шектеулер жүйесінің алдыңғы m векторын бірлік векторлар деп есептейміз, одан сызықты функцияны
Табу керек ең кіші ең үлкен мәнін.
(4) - і формуланың векторлық түрде жазылуы.
мұндағы:
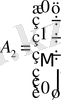 ,
,
жоспарын аламыз. Бұл жоспарға
жіктеуі сәйкес. Мұндағы сызықты тәуелсіз демек құрылған алғашқы жоспар тірек жоспар болып саналады. Алғашқы (6) жоспары екінші тірек жоспарға өтетіндігін тексереміз
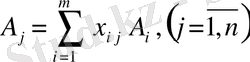 (8)
(8)
Базиске кірмейтін
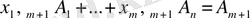 (9)
(9)
Жіктеудегі
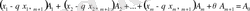 (10)
(10)
Егер ком - рі теріс болмаса
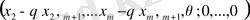 векторлары жоспар болып құрамына
векторлары жоспар болып құрамына
(11) =>
- Тиімді жоспар іздеу тиімділік шарты
Сызықты программалау есебі (1) - (5) жоспарлары бар және оның әр жоспары тәуелсіз онда (6) тірек жоспары үшін
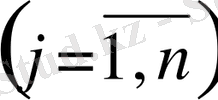
Мұндағы
Теорема : Егер кез келген
Теорема : Егер кез келген
- Симплекс әдісінің алгоритмі
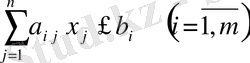 (2)
(2)
С
базис
- Бастапқы тірек (немесе базистік) жоспарын құрамыз қосымша теріс емес айнымалылар енгізіп, теңсіздіктер жүйесіне теңдіктер жүйесіне көшеміз.
Қосымша теріс емес
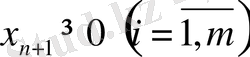 айнымалылары базистік болып табылады, себебі (4), (5) теңдеулер жүйесінің коэффициентін құрылған мақсаттық соңғы М бағанда сызықты тәуелсіз бірлік матрица демек осы бағандарға сәйкес келетін теріс емес айнымалыларда
айнымалылары базистік болып табылады, себебі (4), (5) теңдеулер жүйесінің коэффициентін құрылған мақсаттық соңғы М бағанда сызықты тәуелсіз бірлік матрица демек осы бағандарға сәйкес келетін теріс емес айнымалыларда
- Құрылған жоспарға тиімділік шартының орындалуын тексереміз. жоспары тиімді болу үшін индекстік жолдың барлық коэффициенті (- н басқалары ) сызықты программалау есебінmaxшешкенде теріс емесminоң емес болса жеткілікті. Егер тиімділік шарты орындалса есеп шешіледі. Базистік айнымалылар және бос мүшелер бағандарында сәйкесінше құрылған тиімді жоспарлар компоненттері, индекстік жолмен бос мүшелер бағанының қиылысындасызықты формуланың экстрималды мәні орналасқан.
- Егер тиімділік шарты орындалса онда есептімахшешкенде индекстік жолдың теріс коэффициенттік обсолюттік шамаларының үлкенін, алminиндекс жолдың оң коэффициент ең кішісін таңдаймыз. Таңдалған ең үлкен коэффициент сәйкес бағанда шешуші деп аталады. Шешуші баған қандай айнымалының базиске кіретінін көрсетеді.
- Бос мүшелер бағана элементтерінің шешуші бағанының тек оң элементіне қатнасын есептейді. Егер ондай элементтер жоқ болса сызықты программалау есебінің шешімі жоқ және олардыбағанына жазады. бағанының барлық элементтер ішінен ең кішісін таңдайды. - ң ең кіші мәніні ие симплекс кестенің жолын шешуші деп айтады. Шешуші жол қандай айнымалының базистен шығатынын көрсетеді. Шешуші баған мен жол қиылысқан жерде бас элемент тұрады.
- Сиплекс кестесін келесі тәртібіне толтырамыз:
а) Шешуші бағанға сәйкес бос айнымалыны базистік айнымалыға енгіземіз АМ шешуші жолға сәйкес базистік айнымалыны бос айнымалыларға ауыстырамыз.
б) Жаңа кестенің бағыттауыш жолын толтырамыз, ол алдыңғы кестенің шешуші жолының элементтерін бас элементке бөлу арқылы құралады.
в) Шешуші бағанға сәйкес бос айнымалыны базиске көшіру үшін оны бағыттаушы жолдан басқа барлық жолдардан алып тастау қажет. Ол үшін алдынғы кестені шешуші бағанына сәйкес бағанның қалған барлық ұяшықтарына Гаус әдісімен 0 - дер жинаймыз. Симплекс кестелерінде есептеулерді симплекс белгісі орындалғанша жалғастырамыз.
2 Есептің қойылымы
Параметрлік программалау есебін Cимплекс әдісі бойынша шешу.
F=(2+t) x
1
-(3-t) x
2
+3(2+4t) x
5
 max
max
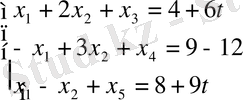
x 1 , x 2 , …, x 5
Шешімі: есепті стандарты түрде келтіреміз:
F=(2+t) x 1 -(3-t) x 2 +3(2+4t) x 5
x 1 , x 2
1-ші симплекс таблицаны құрамыз:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz