Екілік, сегіздік, ондық және оналтылық санақ жүйелері: түрлендіру әдістері мен арифметикалық амалдар


Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 19 бет
Таңдаулыға:
Жоспар
Кіріспе
Cанақ жуйелері.
Негізгі бөлім:
1. Сегіздік және екілік жуйелердің арасындағы байланыс.
2. Екілік жуйедегі арифметикалық операциялар.
3. Әр түрлі жүйеде берілген сандарға арифметикалық амалдар қолдану
4. Практикалың жұмыстар. Жаттығулар
5. Дұрыс бөлшектерді бір санау жүйесінен екінші санау жүйесіне көшіру.
Кіріспе
Cанақ жуйелері.
Берілген санды көрсету үшін қолданылатын белгілер және ережелер жиыны санақ жуйесі деп аталады.
Санақ жүйелері тұрған орнына байланысты мағынасын өзгертетіндер (позициялықтар) және өзгертпейтіндер (позициялық еместер) болып екіге бөлінеді.
Өзгеретін санау жүйесінде цифрдың мағынасы оның орналасқан позициясына байланысты өзгереді. Мысалы, 555. 5 қай позицияда тұруына байланысты 5 цифрдың мағынасы өзгеруде.
Өзгермейтін сандар жүйесінде цифрдың тұрған орны оның мағынасын өзгертпейді. Мысалы, римдік сандық жүйелер. XXX санында X -ондық санның белгісі және оның мағынасы тұрған орнына байланысты өзгермейді.
Компьютерлерде санды жазу басқа жүйелерге; арағанда жинақы және есептеуге ыңғайлы позициялық сандық жүйе қолданылады.
Тарихи деректер бойынша ондық санау жүйесі ең көп тараған жүйе болса да, онымен қатар көптеген сандық жүйелер осы күнге дейін адам өмірінде қолданылып келеді. Мысалға, индейцтер - бестік- ондық, Европада - он екілік (дюжина), ал Қытайда - бестік жүйелерді қолданады.
Негізгі бөлім
Негізінде кез келген сандық жүйе құруға болады. Сандык жүйенің негізі ретінде кез келген бүтін санды, мысалы, 2, 3, S және т. б. қабылдап, соларға сәйкес екілік, үштік, сегіздік және басқа да сандық жүйе-лер құруға болады.
Өзгеретін сандық жүйеде кез келген негізге мынадай қағида дұрыс келеді қарастырылып отырған разрядтағы бірлікте о алдыңғы разрядтың бірліктерінен қанша есе көп екенін көрсететін сан, сол сандық жүйенің негізі болып есептеледі. Сондықган кез келген позициялық сандық жүйеде тұрған санды төмендегідей түрде жазуға болады:
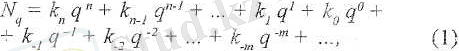
Мұндағы N - q - сандық жүйеде тұрған сан;
q - жүйенің негізі;
п - разрядтың немері;
к п - қарастырылып отырған разрядты ң бірлік санына тең.
коэффициент.
К і - ондық санақ жүйесінде қабылдайі ын мәндері 0, 1, 2,
3, 4, 5, 6, 7, 8, 9, яғни кез келген жүйеде Ц қабылдайтын
мәні 0, 1 . . . q-1.
Мысалы, 35. 72 - саны үшін, Бұл коэффициент осы санның бір-бірінен кейінгі цифрларының мэні, яғни 3, 5, 7, 2.
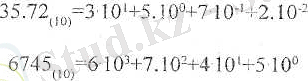
немесе
Ондық санақ жүйесінде компьютерде иыформацияны өндеу ыңғайсыз, себебі есептеу машиналардың негізгі жұмысшы элементтері екі позицияда ғана болады: "Қосылған", "Айырылған" және т. б.
Компьютерде мәліметтерді екілік жұйеде өңдеу өте ыңғайлы. Екілік жүйеде санның кез келген разряды тек 0 және 1 цифрларының тізбегімен өрнектеледі, ал мұндай цифрлардың физикалық моделін құру техникалык тұрғыдан қарағанда өте оңай. Техникада көптеген тетіктер екі тиянақты жағдайда болуы мүмкін. Мысалға, реле: контактылар қосылған - модель - 1, айырылған - модель - 0.
Екілік санақ жұйесінің негізін 1850 ж. ағылшын ғалымы, математик Дж. Буль ойлап тапқан. Бұл жүйе екі цифрмен 0 және 1 өрнектеледі. Бұл жүйенің түбірі - 2.
100100 екілік санын мынадай түрде жазуға болады:
100100 2 = 1 -2 5 +02 4 +02 3 +1 2 2 +02 : +0-2°.
Екінші буынға жататын компьютерлерде сегіздік сандық жүйе де қолданылды. Бұл сегіздік санақ жүйе, машинаға есепті бағдарламалауға дайындағанда, команданы жазу, машинаға енгізу үшін қолданылады.
Сегіздік сандық жүйеде тек 0-ден 7 дейінгі цифрлар қолданылады.
2. 8. Берілген санды әртүрлі санақ жүйелерінде өрнектеу.
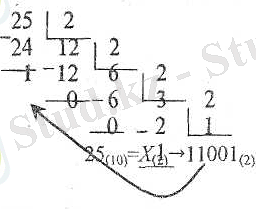
а) Бутін санды көшіру ережесі. Ондық санды басқа санақ жүйеге көшіру үшін оны жаңа жүйенің түбіріне рет-ретімен бөліп, қалған қал-дықтарды ақырғысымен қоса, алынған тәртібіне керісінше жазу керек.
Мысалы, 25 екілік сандық жүйеге көшір
б) Бөлшек санды баска жүйеге көшіру ережесі. Санньщ бөлшегі жаңа жүйенің түбіріне көбейтіледі. Көіліру процесі үтірден кейін Kan-
ma разрядқа дейін жүргізілу керек болса, сонша разрядқа дейін жүргізіледі.
Мысалы, 0. 3125 (10) Х Х (2) Х0. 0101 (2)

в) Аралас бөлшек санды басқа жүйеге көшіру. Аралас бөлшек сандарды басқа жүйеге көшіру үшін алдымен бүтін сан, сонан кейін бөлшек сан, жоғарыдағы көрсетілген ереже бойынша жаңа жуйеде өрнектеліп, нәтижелер бірге жазылады.
Мысалы, 25. 5 (10) Х Х (2) Х11001. 1 (2)
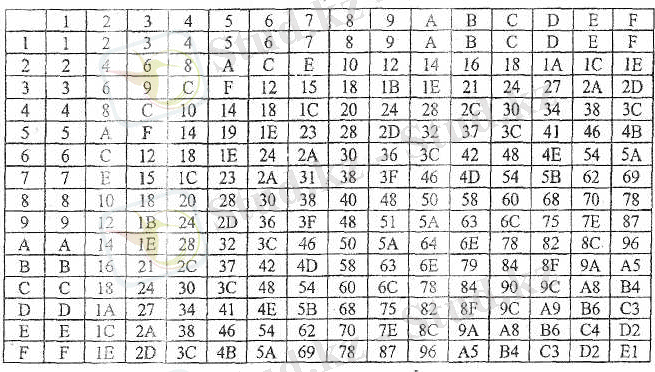
Кесте 1
Әр түрлі өзгеретін сандықжуйеде сандарды жазу
16-лық
q =16
10-дық
q =10
8-дік
q =8
2-лік
q =2
0
1
2
3
4
5
6
7
8
9
А
В
С
D
E
F
10
11
12
13
14
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
0
1
2
3
4
5
6
7
10
11
12
13
14
15
16
17
20
21
22
23
24
0
1
10
11
100
101
110
111
1000
1001
1010
1011
1100
1101
1110
1
10001
10010
10011
10100
Сегіздік және екілік жуйелердің арасындағы байланыс. Прак-тикада, бағдарлама кұрғанда (үшінші буынды машиналарға дейін) ко-манданың нөмірі, санның адресін, операцияның кодын, алғашқы мәліметтерді және т. б. сегіздік жүйеде өрнектеледі. Бірақ, компьютерлердегі барлық ақпарат тек екілік жүйеде ғана жазылды. Сондыктан, компьютерлерде арнайы құрал арқылы "триад" таблицасының көмегімен информацияны сегіздік жүйеден екілік жуйеге ауыстырады. Үлкен сандарды екілік жүйеге ауыстыру өте үлкен есептеуді қажет ететіндіктен, оларды алдымен сегіздік жүйеге, содан кейін "триад" таблицасын қолданып екілік жүйеге ауыстырған жөн.
Кез келген сегіздік жүйеде өрнектелген санды "триад" таблицасын қодданып оңай екілік жүйеге кешіруге болады.
Кесте 2
Екілік "триад"

Санды екілік жүйеден сегіздік жүйеге көшіру үшін, оны үш-үш цифрдан топ-топқа бөледі, әр бүтін санды топ-топқа бөлу үтірден солға қарай басталады да, ал бөлшек жағы үтірден оңға қарай жүреді.
Бірінші және ең ақырғы санды, үш цифрға толғаиша нольмен тол- тырады да, әр үш цифрдағы топты сегіздік жұйенің цифрларына ауыс-тырады, Мысалы, 11011101. 1011 (2) -»Х (8)

Осындай бірінен-біріне механикалык көшіру ретімен, клавиш (тетік) құрылысы арқылы перфоратор сегіздік жүйеде жазылған бағдарламаны екілік жүйеге ауыстырып компьютерге енгізеді.
Екілік-ондык кодтар (жуйелер) . Екілік-ощ. ық кодтар аралык жүйе болып есептелінеді. "Тетрада" таблицасынық көмегімен, арнайы құрылыстар, ондык сандарды клавиатурамен терген кезде екілік-он-дық кодтарға айналдырады да, ал машинаыың өзі бұл кодттарды екілік жүйедегі сандарға көшіреді.
Машина есептік қорытындысын екілік жүйеде а лады да, оны екілік- ондык кодтарға көшіреді. Бұдан ісейін арнайы құрылыс аяқкы қоры-тындыны кэдімгі ондық жүйеге көшіреді. Мысальі, мына санды:
2795 (21) ->Х (2-10) , екілік ондық кодта жазайык.
Кесте 3
Екілік тетряд
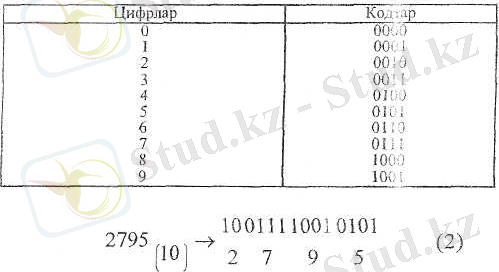
Екілік-ондық кодтағы орнек екілік жүйедегі сандарға сәйкес емес. Санды екілік-ондық кодтан ондық жүйеге көшіру жоғарыдағы тәртіпке сәйкес.
Мысалы,

Екілік жуйедегі арифметикалық операциялар. ЭСЕМ-де ариф-метикалық әрекеттер қалай жүргізіледі? Бұл сұраққа жауапқа беру үшін, екілік жүйеде арифметикалық операциялар қалай жүретінімен танысайық. Себебі компьютерде арифметикалық әрекеті ер негізінде екілік жүйеде жүреді.
ЭСЕМ жасалмай тұрып, 1850 ж. ағылшын математигі Дж. Буль екілік алгебраны сұрастырып шықты (Қазіргі кезде бұл алгебраны, математикалық логика деп атайды) .
Кесте 4
Екілік сандардың арифметикасы
0+0=0
0+1=1
1+0=1
1+1=10
0-0=0
1-0=1
1-1=0
10-1=1
0х0=0
0х1=0
1х0=0
1х1=1
Сегіздік савдардын арифметикасы Қосу кестесі
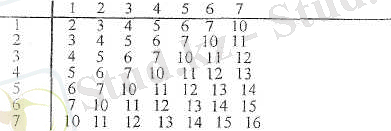
Кебейту кестесі

Екілік жүйеде әр тұрлі арифметикалық операцияларды орындау үшін мына ережелерді білу керек.
Ескерту: бірнеше қатар сандарды косу тәсілі кебейту амалын орындау үшін қажет.
Азайту амалын орындағанда, көрші разрядтан қарызға алынған бір кіші разрядта екі бір болып ауыстырылатынын әрқашан еске алу керек.
Егер көрші разрядттарда нөлдер болса, онда, көптеген. жоғарғы нөлдік разрядттан кейін, бірді карызға алуғатура келеді. Мұндай уақытта барлык жоғарғы нөль разрядтарда бір-бірден бір болады да, ал көрші ең кіші разрядта екі бір болады.
Мысалы:

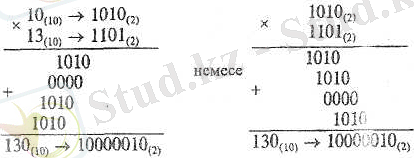
Көбейту ережесі бойынша, нөлые көбейткенде әрқашанда нөль береді де, ал бірге көбейткенде сан өзгермейді. Сондықтан да, көп орынды санды екілік жуйесінде көбейту тек сан қатарын оңға немесе солға жылжытып, бір қатарға сатылай жазып, қосу амалын орындаса болғаны.
Мысалға, 10қ13=130.
Бөлу амалын орындауда көбейту және алу ережесі қолданылады.
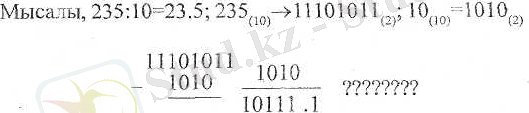
Бөлу амалының дұрыс орындалғанын тексерейік:
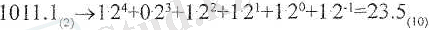
Қазіргі кезде барлық халық шаруашылығы салаларында дербес компыотерді кең қолдануға байланысты компьютерлерде есеп шығару жұмысында жаңаша езгерістер пайда болды. Бұрынғы буындағы ком-пьютерлерге кажетті кейбір дайындық жұмыстары, атап айтқанда: мәліметтерді өңдеуге дайындау, оларды тасығыштарға (перфокартарларда, перфоленталарда, оперативтік жадыда т. б. с. с. ) калай жазылатын, қалай оқылатын, машинаның информацияны калай ұғатын, информацияны кодтау; "тура", "керісінше" және "косымша" кодтау жолдары, машинада кодтармен арифметикалық амалдарды орындау тәсілдері, компьютердің физикалык жұмыс істеу принциптері т. б. с. с. тақырыптар кітапта әдейі карастырылмайды. Себебі, бүгінгі компьютер пайдаланушыларға, оның ішінде ауыл шаруашылығы мамандарына, бұл тақырыптарды оқудың келешек жұмыстарына қажеті шамалы.
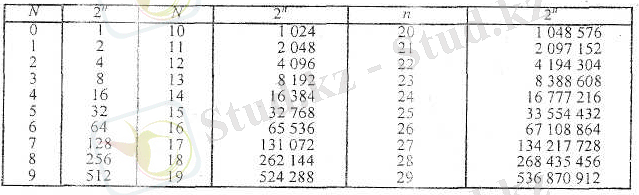
Кесте 5
2 санының дәрежелері
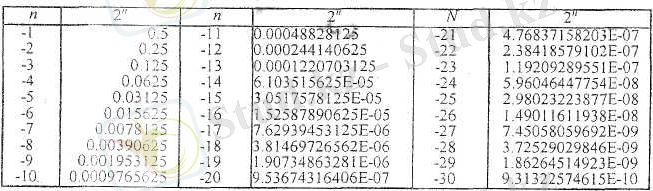
Кесте 6
2 санының дәрежелері
Кесте 7
8 санының дәрежелері
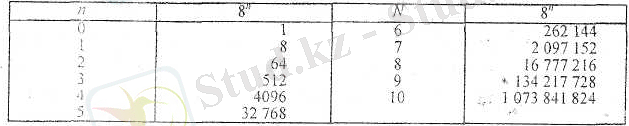
Кесте 8
8 санының дәрежелері

Кесте 9
16 санының дәрежелері

Кесте 10
16 санының дәрежелері

Кесте 11
Қосу кестесі
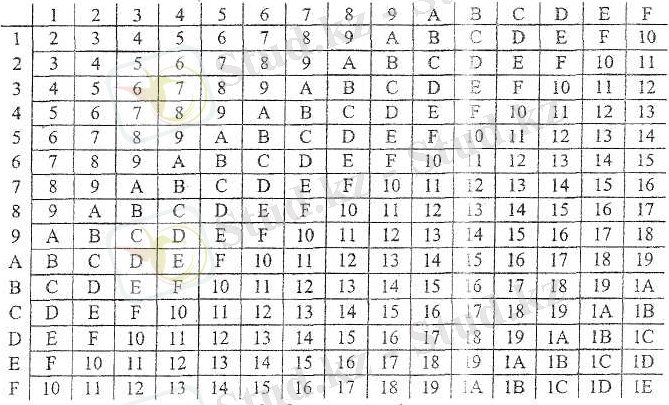
Кесте 12
Көбейту кестесі
2. 9. Әр түрлі жүйеде берілген сандарға арифметикалық
амалдар қолдану
Әр түрлі жүйелердегі сандарға арифметикалық амалдар қолдану ережесі ондық сандарға амалдар қолдану ережелерімен бірдей.
17. 1011, 1 + 101, 01 амалын орындаңдар.
Шешуі.


Барлық амалдарды ондық жүйеде орындауға қалыптасып қалғандықтан, сегіздік жүйедегі сандарға арифметикалық амалдар қоддану қиынға түседі. Мұнда амалдар сегіздік жұйеде жүргізілуі тиіс, сондықтан сегіздік жүйеде кестені пайдалану ыңғайлы.

25. Бөлшександарды бір негізден екінші негізге көшіру әдісін пай-даланып, 0, 752 8 санын ондық негізде өрнектеңдер.
Шешуі. Арифметикалық амалдарды тек бір негіздегі сандарға ғана пайдалануға болады, яғни 10 10 = 12 8 .

26. Сегіздік негіздегі сандарға косу және азайту амалдарын колданыңдар:

27. Сегіздік негіздегі сандарға көбейту және бөлу амалдарын колданыңдар:
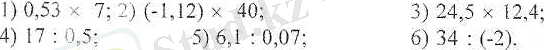
Шешуі.
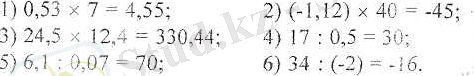
Практикалың жұмыстар
Жаттығулар
1. Екілік негізде берілген:
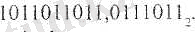
сандарын 16-лық және 8-дік жуйелерде калай жазады?
Шешуі. а) екілік жүйедегі санды 16-лық жүйеге аудару үшін төрт-төрттен бөліп, әрбір төрт разрядка сәйкес 16-лық цифрды (символды) жазу жеткілікті. Төрт орынға толмаған жағдайда бөлшектің соңында және бүтін бөліктің алдында нөлдер бар деп есептелінеді
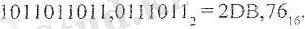
б) осы санды 8-дік жүйеге көшіріп жазу үшін де жоғарыдағы ереже пайдаланылады, бірак онда үш-үш орыннан бөлінеді:
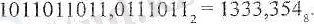
2. 16-лық негіздегі 6А7, 8 және 765, 45 сандарын екілік жүйеде өрнектеңіз.
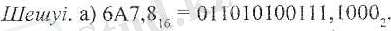
Мұнда санның басынан бастап әрбір цифрын екілік жүйеде жазып шығамыз, жоғарыда айтылған ережеге сүйенсек, санның алдындағы, соңындағы нөлдерді жазбауға болады, ендеше,
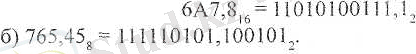
3. Ондык санау жүйесінде (р = 10) берілгенN 10 = 557 санды. сегіздік
(q = 8) жүйеде жазыңдар (р > q) .
Ереже бойынша бөлу былайша орындалады:
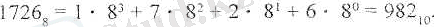
Сонымен, N 8 . = 1221 8 . болып шықты.
4. Сегіздік санау жүйесінде берілген N 8 = 1726 8 санды ондық санау жүйесіне көшіріңдер. Мұнда р = 8, q = 10, яғни р < q. Бұл есепті шығару үшін мына екі жолдын, біреуін пайдалану керек:
1) Жоғарыдағы (1) формула бойынша есептеу:
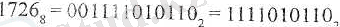
Яғни: 1726 8 = 982 10 .
2) Бүтін сандарды бір негізден екінші негізге көшіру. Бұл есепте р < q, ендеше ең алдымен q-ді р санау негізіне көшіру ушін жоғарыдағы ережені пайдалану керек, есептеулер р негізінде жүргізілуге тиіс.
.

11 8 , 10 8 , 2 8 - цифрлары 8-дік негіздегі цифрлар, олардың ондық жүйедегі мәндері мынадай:
2 8 , = 2 8 , = 10 8 = 8 10 , ендеше: 1726 8 = 982 10 .
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz