Операцияны зерттеу процесі

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:

Кіріспе

Операцияны зерттеу дегеніміз автоматты басқару жүйесін басқару есептерін шешуге қолданған ғылыми тәсіл.

Операцияны зерттеу процесі кезіндегі мақсат: механикалық - экономикалық немесе басқа да сипаттағы шектеулерге ие, ұйымдастырылған басқару есептерін шешудің ең тиімді әдісін қолдану. Жүйелердің моделін құру және олардың сипатамаларын анализдеу кезінде математикалық әдістердің қолдануын операцияны зерттеу деп түсінуге болады. Операцияны зерттеу дегеніміз - белгілі мақсатқа жеткізетін және нақты ниетпен біріктірілген шаралар жиынтығы.

Операцияны зерттеуді ұйымдасқан басқару есептерін шешудің құралы деп - есептей отырып, ғылым және өнер ретінде де қарастыруға болады. Әр сала құрылымы жағынан ұқсас, бір қатар ұқсас белгілері бар. Ұқсас әдістермен шешілетін операцияны зерттеудің есептері деп атауға болатын есептер жиі кездеседі. Осы есептердің шешіміне қол жеткізу үшін операцияны зерттеудің математикалық, сандық әдістері қолданылады. Операцияны зерттеу процесін келесі этаптарға бөлуге болады:

Мәселелерді сұрыптау;
Модель құру;
Модель қолдану арқылы есепті шешу;
Модельдің адекваттылығын тексеру;
Зерттеу нәтижелерін іске асыру.

Операцияны зерттеудің маңызды моделі болып математикалық модель табылады. Бул моделден басқа операцияны зерттеуде имитациялық және эвристикалық модельдері қолданылады.

Операцияны зерттеу негіздерінің негізгі әдістері болып келесілер табылады: сызықтық бағдарламалау әдістері болып келесілер табылады:сызықтық бағдарламалау әдістері, транспорт әдісі, бейсызықты бағдарламалау әдістері, әдістері, ойындар теориясының әдістері.

Материалдарды оптималді пішімдеу.

Математикалық бағдарламалар есептерінің ішінде ең қарапайым болып сызықтық бағдарламалау есептері табылады.

Сызықтық бағдарламалау тиімділіктің W сызықтық көрсеткіші x ₁ , x ₂ , . . . x _n элементтерінің шешімінің байланысынан және x ₁ , x ₂ , . . . x _n сызықтық теңдігі немесе теңдіктерінен тұратын элементтердің шешімінен құралған шектеулерден тұрады. Бұндай есептер практика екзінде жиі кездеседі, мысалы, өндірісті жоспарлау, оптималды ассортиментті анықтау, резисторды реттеу және тағы басқа.

Сызықты бағдарламалаудың негізгі есебі мынандай түрде жазылады.

Z=p ₁ x ₁ +px+…+p ₂ x ₂

Осы тапсырмаға байланысты m>n сызықтық теңсіздігі берілген.

a _i1 x ₁ +a _i2 x _i2 +… a _i , I=1, m

Бұл берілген теңсіздікті келесі түрде жазамыз:

Y _i =-a _i1 x ₁ -a _i2 x ₂ -…-a _in x _n +a _in 0

Берілген сызықтық бағдарламалаудың есебін шешудің негізгі әдісінің бірі болып Данцигтің симплекс әдісі табылады.

Симплекс әдісінің аморифмі сызықтық теңсіздіктер жүйесінен тіректі шешім табудан тұрады. Симплекс әдісін қолдану арқылы оптималды ассортиментті анықтауды келесі мысалда көруге болады.

Мысалы а ₁ , …а _i , . . . а _p мөлшерден Р түрлі ресурстар о түрлі бұйымдарды қолданылады.

А=// а _ik // матрицасы берілген, мұндағы а _ik бұйымның бірлігіне кететін к- ші ресурстың шығынының нормасын сипаттайды. (к= 1, 2, …, q) к-ші бұйымның шығарылу бірлігінің тиімділігі с _к көрсеткішімен сипатталады. ‘сызықтық’ шартын қанағаттандыратын α ₁ бұйымының с ₁ көрсеткіші және α ₂ бұйымының с ₂ көрсеткіші с ₁ α ₁ + с ₂ α ₂ теңдеуіне тең. Өнеркәсіптің шығарған к бұйымының бірлік мөлшері х _к ≥ 0 деп белгілейміз.

Осы сияқты түрде берілген мысалдарды оптимальді ассортиментті анықтауға жатқызуға болады. Бұл мысалдың шешімін табу үшін, бұның математикалық моделі максимальді түрдегі мына формулаға тең болады:

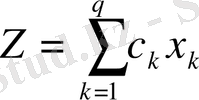
Бұл формуланы алу үшін, ең алдымен мынадай шарт болуы керек:

(I=1, 2, …; p)

Есептің математикалық моделінде бұл шарттың басқа да көптеген шарттар мен шектеулер де болуы мүмкін. Осындай түрде берілген есептреді өте тиімді жолмен шығарудың бірден-бір жолы болып симплекс әдісі табылады. Оптималды ассортиментті анықтау үшін тиімді, әрі қолайлы әдістерді пайдаланған жөн.

2. Есептің математикалық моделі

Математикалық модель - есептеулер жүргізуге мүмкіндік беретін операцияның қызметінің сипаттамалық заңдылықтары. Зерттелінетін операция туралы ақпарат аз болған жағдайда қарапайым сызықтық модельді құрудан бастаған дұрыс.

Модель дегеніміз - ақиқатты, нақты белгілеу. Модельдің көмегімен есептеуге және болжауға болады. Модельді тұрғызу үшін тәуелсіз және тәуелді айнымалыларды енгізу қажет.

Модель құру этапы екі ішкі этаптан тұрады:

айнымалыларды енгізу;

Модель құру айнымалыларды анықтау мен енгізуден басталады. Тәуелсіз айнымалылар деп - есептің шарты бойынша анықталатын белгісіз жоспар немесе басқару әрекеті айтылады.

шектеулерді және мақсатты функцияны құру;

Есепті бір немесе бірнеше шектеулер болуы мүмкін. Мақсатты функцияны құру үшін осы шектеулерді қолданамыз.

Берілген есептің математикалық модель келесідей болады.

Айнымалылар: x ₁ , x ₂ , x ₃ , x ₄ ;

Оптималды ассортиментті есептеуге керекті қосымша шарттар: x ₁ 5;

x ₂ 8; x ₃ / x ₄ =1/2; 2x ₃ =x ₄ ;

x _j _{Equation. 3} 0, (i=1, 2, 3, 4) -I қасиетпен бөлінетін өнім саны.

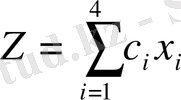→ max - мақсатты функция.

Y ₁ =3x ₁ +5x ₂ +2x ₃ +4x ₄ 60

Y ₂ =22x ₁ +14x ₂ +18x ₃ +30x ₄ 400

Y ₃ =10x ₁ +14x ₂ +8x ₃ +16x ₄ 128

Y ₄ =x ₁ 5

Y ₅ =x ₂ 8

=2x3-x4

y ₁ =-3x ₁ -5x ₂ -2x ₃ -4x ₄ +60 0

y ₂ =-22x ₁ -14x ₂ -18x ₃ -30x ₄ +400 0

y ₃ =-10x ₁ -14x ₂ -8x ₃ -16x ₄ +128 0

y ₄ =-x ₁ +5 0

y ₅ =x ₂ -8 0

0=2x ₃ -x ₄

Есептің шығару әдісінің теориясы.

Сызықтық бағдарламалаудың 2 айнымалысы бар есепті шығару барысында алгебралық аппаратты қолдану қажет. Сонымен қатар сызықтық бағдарламалаудың жалпы есеп шығару әдісінің бірі симплекс әдісін қолдану өте тиімді.

Симплекс әдісінің көмегімен алыған ақпарат айнымалылардың оптималды мәнімен ғана шектелмейді. Симплекс әдісі - бұл көптеген оптималдық есептерде қолданатын итерациялық есептеулермен сипатталады. Симплекс әдісін қолдану барысында итерацияның максималды саны сызықты бағдарламалау есебінің базистік шешімінің максималды санына тең болады. Бұл дегеніміз симплекс әдісінің итерациясының саны C Equation. 3 =n ! /[(n-m) !m! ] мәнінен аспайды.

Симплек әдісінің есептеу схемасының негізін түрлендірілген жордан шығарулары құрайды rs-ші а-шешуші элементі бар түрлендірумен жордан шығаруының бір қадамы алғашқы кестені жаңа кестеге 5

ережемен аударады.

Шешуші элемент бірлікке ауыстырылады.
Шешуші жолдың қалған элементі сол күйінде қалады.
Шешуші бағанның қалған элементінің таңбасын ауыстырады.
Қалған элемент мына өрнекпен табылады: aEquation. 3 =aijars-aisarj
Жаңа кестенің барлық элементі шешуші элементке бөлінеді.

Симплекс әдісінің 2 түрі бар:

Тіке симплекс әдісі.
Қос мағыналы симплекс әдісі.

Бұл екі түрінің айырмашылығы мынада;

Тіке симплекс әдісінде 2 бөлім бар:

Тіректі шешімді табу.
Оптималді шешімді табу,

Ал қос мағыналы симплекс әдісі керісінше шығарылады: 1. Оптималді шешімді табу. 2. Тіректі шешімді табу.

Тіке симплекс әдісінің алгоритмі.

І Симплекс кестені толтыру.

-x ₁ -x ₂ -x _n 1

y ₁ a ₁₁ a ₁₂ a _1n a ₁

y ₂ a ₂₁ a ₂₂ a _2m a ₂

y _n a _m1 a _m2 a _mn a _m

-p ₁ -p ₂ -p _n 0

II. Еркін айнымалыларды шығарып тастау. Мысалы, барлық х _j - шілер еркін айнымалылар болсын, онда түрлендірілген жордан шығарылулары n-рет қолданып, 2-ші кестені табамыз.

-y ₁ - y ₂ -y _n

x ₁ b ₁₁ b ₁₂ b _1n

x _n b _n1 b _n2 b _nn

y _n+1 b _{n+1, 1} b _{n+1, 2} b _{n+1, n}

y _m

z=p ₁ x ₁ +p ₂ x ₂ +…+p _n x _n max

әрбір x _j -ң сәйкес өрнегін жазып, оларды кестеден сызып тастаймыз.

X ₁ =-(b ₁₁ y ₁ +b ₁₂ y ₂ +…+b _1n y _n ) +b ₁

X _n =-(b _n1 y ₁ +b _n2 y ₂ +…+b _nn y _n ) +b _n

Жұмысты 3-ші кестемен жалғастырамыз.

-y ₁ -y ₂ -y _n 1

y _n+1 b _{n+1, 1} b _{n+1, 2} b _{n+1, n} b _n+1

y _m b _m1 b _m2 b _mn b _m

z q ₁ q ₂ q _n Q

ІІІ. Кестедегі о-ші жолды шығарып тастау. Шешуші элементті таңдаудың ережесі:

Шешуші баған ретінде кестенің bkl>0 оң мағыналы баған таңдалынады.
Оң мағыналы еркін мүшелердің шешуші баған кооэфицентіне қатынасы есептеледі. Олардың ішінен ең кішісі таңдалынады. Сөйтіп шешуші элемент табылады. Түрлендірілген жордан шығарулары бір рет орындалады.

IV. Тіректі шешімді табу.

Егер барлық бос мүшелер оң мағыналы болса, онда тіректі шешім табылады.

Y ₁ = y ₂ =…=y _n =0

Y _n+1 =b _n+1

Y _m =b _m

Z _T =Q _(T)

X _n {x ₁ , x , …, x }

Егер бос мүшелер арасында теріс мағыналы мүшелер болса, онда тіректі шешімді табатын, келесі шешуші элементті таңдаудың ережесін қолданамыз.

Теріс мағыналы мүшесі бар жолды таңдаймыз.
Осы жолдың коэфицентінің арасында теріс мағыналы коэфициенттер бар болса, арасынан біреуін таңдаймыз да сол коефициентті бар бағанды шешуші баған деп есептейміз.
Бос мүшелердің бағанының коэфициентерінің оң мағыналы қатынастарын есептейміз де, арасынан ең кішісін таңдаймыз. Түрлендірген жордан шығаруларын бір рет жүргіземіз

V Оптималды шешімді табу.

Егер Z-ші жолдың барлық коэфициенті оң мағыналы болса, онда есептің оптималды шешімі бар деп есептейміз.

Y = y =…=y =0

Y =b _n+1

Y =b _m

Z ^* Q

X ^* {x , x , …, x }

Егер Z-ші жолдың коэфициентінің арасында теріс мағыналы коэффициенті болса, онда оптималды шешімді табатын шешуші элементінің ережесінқолданамыз.

Теріс мағыналы коэффициенті бар бағанды шешуші баған ретінде қарастырамыз. Егер теріс мағыналы коэффициенттері көп болса, онда арасынан абсалюттік шамада ең үлкенін аламыз.
Осы бағанның барлық оң мағыналы коэффициентін аламыз, сәйкес бос мушелерді оларға бөлемізде арасынан ең кішісін таңдаймыз да, түрлендірілген жордан шығаруларын бір рет қолданамыз.

Тіке симплекс әдісі бойынша есепті шығарған кезде, біз көп жағдайда сызықты фунцияның максималдық белгісін аламыз. Алегерде минимум формасында берілсе келесідей жазамыз:

Z=-z=-p ₁ x ₁ -…-p _n x _n

Min z=-max z

Сызықтық бағдарламалауда шектеулер теңсіздік күйде және теңдікпен, кей кезде аралас түрде беріледі. Симплекс әдісінің алгорифмі біртипті алгорифмге жатады.