Итерациялық тәсілдер

Пән: Автоматтандыру, Техника
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 12 бет
Таңдаулыға:

Кіріспе

Көптеген практикалық есептер сызықты теңдеулер жүесі арқылы шешіледі. Сызықты теңдеулер жоғарғы математикада ең көп таралған, әрі маңызды есептер ретінде қолдануы ешбір туғызбайдыю

Онда n сызықты алгебралық теңдеулер мен n белгісіздері бар жүені жазайық:

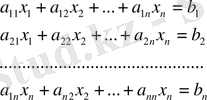
Осы жүйе коэффиценттерінің жиынын таблица түрінде жазып алайық:

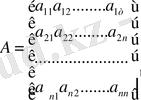
Бұл элементтер таблицасы, ол n қатарлар мен n бағандардан тұрады, n ретті квадраттық матрица деп аталады. Егер осындай матрица mn эллементтерден құралса, m қатар мен n бағандардан құралса, онда ол тікбұрышты матрица деп аталады.

Екеуінен басқа симетриялық матрица ; диогальынан төмен жатқан, нөлге тең элементтерден құралған матрица жоғары үшбұрыштық; клеткалық, ленталық матрецалар және бірлік пен нөлдік матрецалар деген түрлері жетіп жатыр. Сызықты теңдеулер жүелерін шешу көптеген тәсірдер орындалады. Олар екі группаға бөлінеді: тура және итерациялық. Иерациялық тәсілдер - бұл біртіндеп жақындату тәсілдері болып табылады. Бұларда алғаш бастапқы деп аталатын бірінші жақындауды беру қажет. Осыдан кейін кейбір алгоритм арқылы бір цикл есептеулер өткізіледі, ол итерация деп аталады. Бұл итерациядан жаңа жақындауды табады. Осылай итерацияларды қажетті дәлдікке жеткенше орындайды.

Итерация әдісі

Тура тәсілдер белгісіздерді табу үшін формулаларды пайдалынады. Оларды жауапты алдын ала белгілі операциялар орындағынан кейін береді. Бұл тәсілдер қолдануға жеңіл әрі унересальды болып келеді, яғни сызықты жүйелер шешүде жүелердің кен класына жарамды.

Сонымен қатар, тура тәсілднрдің бірқатар жетіспеушіліктері де бар. Әдетте, ЭВМ - де жұмыс істегенде барлық матрицаны есте сақтауды талап етеді. n- нің үлкен мәндерінде жадыда көп орын алынады. Тура тәсілдер матрицаның структурасына көңіл бөлмейді, нөлдік элементтердің коп болған жағдайында, мысалы торлық не ленталық матрицаларда, оларға арифметикалық элемент амалдар орындалып, машина жадысында көп орын алатын болған. Тура тәсілдердің негізгі жетіспеушілігі ондағы есептеу процссінде жиналатын қателік. Бұл әсіресе операциялардың жалпы саны өскенде үлкен жүйелерге, қателіктерге өте сезімтал болып келген жаман шартталған жүелерге қалыпты. Осыған орай тура тәсілде тек тығыс толтырылған матрицасы және нөлге жақын емес анықтауышы бар жүйелерде қолданады.

Атап кететін жай m, сызықты теңдеулер жүесін шешудегі тура төсілдер кейде нақты деп аталады, өйткені шешуі нақты формулалар түрінде жүйенің коэффиценттері арқылы өтеді. Практикада ЭВМ - ді қолданғанда, оған байланысты шығарулар таңбалардың шектеулі саны арқылы жүзеге асады.

Ал итерациялық тәсілдер - бұл біртіндеп жақындату тәсілдері болып табылады. Бұларда алғаш бастапқы деп аталатын бірінші жақындауды беру қажет. Осыдан кейін кейбір алгоритм арқылы бір цикл есептеулер өткізіледі, ол итерация деп аталады. Бұл итерациядан жаңа жақындауды табады. Осылай итерацияларды қажетті дәлдікке жеткенше орындайды. Әдетте, сызықты жүйелерді шешуде итерациялық тәсілдерді алгоритмдері тура тәсілдердікіне қарағанда, қиынырық болып келеді. Есептеулердің қөлемін алдын ала білу қиын.

Осыған қарамастан, итерациялық тәсілдер бірқатар жағдайларда көбірек қолданылады. Олар машиналық жадысында жүйенің бүккіл матрецасы есте сақтауды қажет етудің орнына, тек n компоненттері бар бірнеше векторды есте сақтатқызады. Кейде матрица элементтерін мүлде сақтамай - ақ, керек кезде ғана шығарып есептеуге болады. Әр - бір итерация есептелуін дәлдігі алдында орындалған итерация жауабымен анақталандықтан және алғашқыда орындалған есептеулерге тәуелді болмағандықтан, итерация тәсілдерін қолданғанда жауптар қателіктері жиналмайды. Итерациялық тәсілдердің бұл артылықшылықтары теңдеулердің көптеп жиналған жүесімен кездескенде олрдың өте пайдалы екенін дәлелдейді. Айта кететін жайт, итерацияладың өтуі өте баяу өтеді, сондықтан оны тездету бағытында тиімді жолдар ізестіруде.

Сонымен қатар итерациялық тәсілдер тура тәсілдер арқылы алынған жауаптарды тексеру үшін де қолданылуы мүмкін. Мұндай араласып келген алгоритмдар әдетте тиімді болып келеді. Соңғы жағдайда регуляризация тәсілдері де пайдална береді.

Жоғарыда айтып кеткендей, тура тәсілдер арқылы алынаты жауаптарда қателіктер болады. Бірқатар жағдайлардабұл кателіктерді ескермеуге болмайды, сондықтан оларды ағайтудың әдісін табу қажет. Тура тәсіл арқылы алынған жауапты нақтылау үшін қолданған бір әдісті қарастырайық.

Мына сызықты теңдеулер жүйенің жаубын табайық:

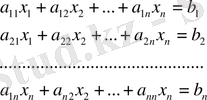(1)

Бір кез - келген тура тәсіл арқылы белгісіздердің жуық мәндері 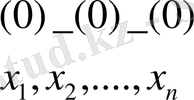табылсын дейік. Осы жауаптарды (1) жүйенің сол жағына қоя отырып, 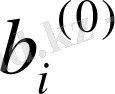- дің 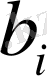- ге тең болмағындағы мәндерің табамыз. (i=1, 2, ……., n) :

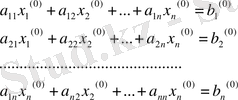(2)

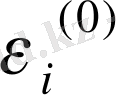- белгісіздердің қателігі, 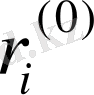- байланыстырушықдеген белгісіздер енгізейік. Яғни:

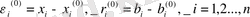(3)

(3) - белгілеулерді ескеріп, (2) тендеулер жүйесінен (1) теңдеулер жүйесін алып, (4) - ті аламыз:

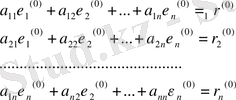(4)

Бүл жүйені шеше отырып, 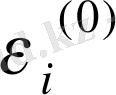қателіктердің мәнін табамыз. Кейін оларды жауапты дұрыстауда қолданамыз. Белгісіздердің келесі жақындытулары мына түрде болып келеді.

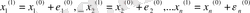Дәл осындай әдіспен 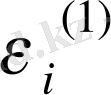- дің жауабына дұрыстаулар, 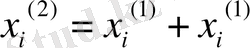Equation. 3 және тағы басқаға жақындауларды табуға болады. Бұл процесс кезекті қателіктердің 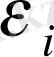мәндері жетерліктей кішірейгенге дейін өтеді.

Жауапты нақтылаудың қарастырылған процессі сызықты теңделер жүйесін шешудің итерациялық тәсілі болып табылады. Кезкті жақындауларды табу үшін, яғни әрбір итерацияда (4) теңдеулер жүйелері (1) теңдеулер жүесінің оң жақтары әртүрлі болған жағдайдағы бірдей матрицалары шығарылатынын ытып өткен жөн. Бұл экономиялық алгоритмдерді құруға өз үлесін қосады. Мысалы, Гаусс әдісін қолданғанда тура қадам этапында есептеу көлемі азаяды.

Қарастырылған әдіс пен итерациялық әдістерінің басқа түрлерін қолданып теңдеулер жүйесін шешу 1 - суретте көрсетілген схемадай өтеді. Бастапқы берілгендер енгізіледі, мысалы, теңдеулер коэфиценттері мен қателіктің мүмкін болатын мәні. Белгісіздердің алғашқы жуық мәнін беру керек. Олар не ЭЕМ- ге енгізіледі, не тура тәсіл арқылы шығарылады. Кейін цікілдік есептеу процессі басталып, әр - бір цикл итерацияны құрайды. Әр итерациядан белгісіздердіңжаңа мәндеріалынады. Қатарынан келген екі итерациядан алынған бұл мәндердің, берілген мүмкін болатын қателіктей, өзгеруі өте аз болған жағдайда, пройесс аяқталады да, соңғы итерациядан алынған белгісіздердің мәндерін шығару өтеді.

Бұл схемада жараудың жағдайы жоқтығы қарастырмаған екенін байқауға болады. Қатарымсыз машинаның уақытын үнемдеу үшін, алгоритмге итерация санын байқап отыратын счетчик енгізіледі. Ол белгіленген мәнге жеткенде есептеуді аяқтайды.

Гаус - Зейдел әдісі

Программаға сағандағы өзінің оңайлығымен ерекшенетін, итерациялық тәсілдердің ең көп таралғандардың бірі Гаусс - Зейдел әдісі болып табылады.

Бұл әдісті (5) жүйені шешумен көрсетейк:

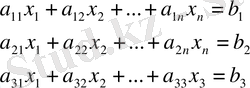(5)

Диагонал 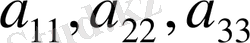Equation. 3 элеметтерді нөлге тең емес деп алып, осы үш теңдеуден сәкесінше 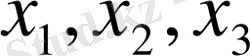Equation. 3 белгісіздерін белгілеп аламыз:

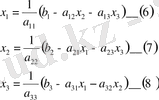Equation. 3

Белгісіздер мәндеріне алғашқы (нөлдік) жақындаулар береміз: 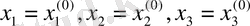Equation. 3 . Осы мәндерді (6) теңтудің оң жағына қоя отырып, 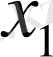Equation. 3 үшін жаңа жақындау аламыз: .

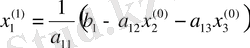Бұл мәнді 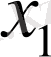үшін, 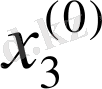жақындауын 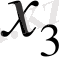үщін қолданып, (7) теңдеудер - ге бірінші жақындауды табамыз: 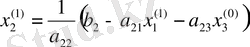. Осыдан Equation. 3 қолданып, (8) теңдеуден үшін бірінші жақындауды табамыз: .

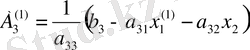Осымен, (6) - (8) жүйенің шешуінің бірінші итерациясы бітеді. Енді 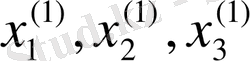Equation. 3 мәндерін қолданып, дәл осы әдіспен екінші итерация жүргізүге болады. Оның нәтижесінде 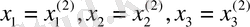Equation. 3 белгісіздер екінші жақындаулары табылады әрі тағы басқа нөмірі бар жақындауды мыны түде корсетүге болады:

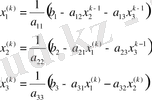Equation. 3

Итерациялық процесс 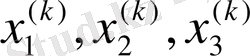Equation. 3 мәндері 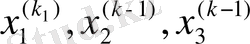Equation. 3 мәндеріне берілген қателіктіктегідей жақын болғанша жалғаса берді. Сонымен қатар итерациялық әдістерді сызықты емес теңдеулер шешуде пайдалануға болады.

Белгісіздің жуық мәнін түрлі әдістер жолымен табуға болады: физикалық қасиеттеріне басқа берілгені бар есепті шешкеніне, графикалық тәсілдеріне байланысты. Егнр бастапқы жақындаудың осындай априорлық бағаларын жүргізү болмайжатса сонда бір - біріне жақын орналасқан a мен b нүктелерінің арасындағы құрамында оң және теріс таңбалары бар үзіліссіз F(x) функциясын аламыз. Яғни F(a) F(b) < 0. бұл жағдайда a мен b нүктелерінің арасында ең болмағанда F(x) = 0 функциясы орындалатын нүкте болуы айқын. 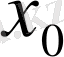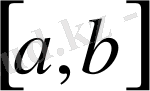Сонда бастапқы жақындау -ді кесіндісінің ортасы етіп аламыз: 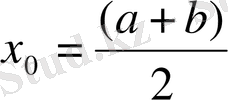итерация нәтижесінде 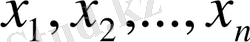Equation. 3 белгісіздер жуық мәндері табылады.

Сызықты емес теңдеулерді шешуде итерацияны қолданудың кейбір әдістерін қарастырайық.

Қақ бөлу әдісі ( бисекция әдісі )

Сызықты емес теңдеулерді түбірлерін табуда жеңіл әдістерінің бірі кесідіні қақ бөлу “ бислекция” болып табылады, оның мәні мынада тұр: 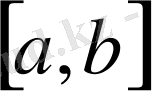Equation. 3 кесіндісін алайық және ізделінді түбір 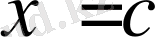Equation. 3 деп белгілейік. Түбірдің бастапқы жақындау ретінде кесіндінің ортасы еті аломыз, яғни 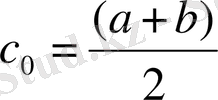Equation. 3 . Енді 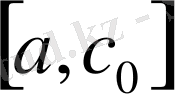Equation. 3 және 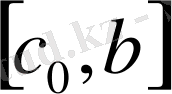Equation. 3 кесінділердегі F(x) функциясының мәндерін зерттейміз. F(x) екі түрлі таңбасы бар кесіндіде ізделінді түбір жатқандықтан, оны жаңа кесінді ретінде аламыз. Бірінші итерация ретінде жаңа кесіндінің ортасын аламыз және тағы сол сияқты кете береді. Осылай әр итерация нәтижесінді түбірі бар кесінді екіге азаяды, яғни n итерациядан кейін ол 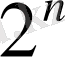Equation. 3 есе азаяды. ( 2 - сурет ) .

F(x) функуиясының мәні n итерациядан кейін кейбір берілген кіші сан - нан модуль бойыншакем болғанға дейін итерациялық процесс жалсады, яғни 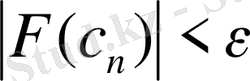Equation. 3 . Сонымен қатар алынған кесіндінің ұзындығы да ескеріледі: оның мүмкін бл\олатын қателіктен кіші болған жағдайында, есептеу бітеді.

3 - суретте F(x) =0 теңдеу түбірін табуының кесіндіні қақ бөлу әдісіндегі итерациялық процесстің блок - схемасы көрсетілген.

Кесіндіні қақ бөлу әдісі көп уақыт қажет ететін әдістердің бірі. Осыған қарамастан оны қолданудың себебі, бұл әдістің, есептің шешімін әрқашанда шығара алатындығында.

Хорд әдісі

Сызықты емес теңдеулерді шешудегі тағы қарастыратын әдісіміз - хордалар әдісі. F(x) функциясының таңбасын ауыстыратын 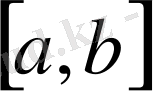Equation. 3 кесіндісін таптық дейік. 4 - суретте көрсетілгендей F(a) > 0, F(b) < 0. Әдістің итерациялық процессі хордалардың абцисса осімен қиылысу нүктелерінің Equation. 3, Equation. 3, . . . F(x) =0 теңдеуінің түбіріне жақындауларынын тұрады.

АВ хорданың теңдеуін табамыз:

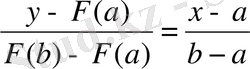Equation. 3

Оның абцисса осімен қиылысу нүктесі үшін мына теңдеу аламыз:

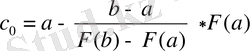Equation. 3 (9)

F(a) мен 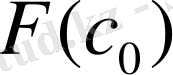Equation. 3 таңбаларын саластыра отырып, F(a) 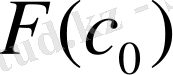Equation. 3 <0 болғандықтан ізделінді түбір (а, Equation. 3 ) интервалында орналасқанын білеміз. 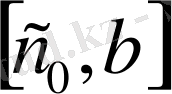Equation. 3 кесіндісін алып тастаймаз. Келесі итерация жаңа Equation. 3 жақындауын ( 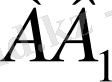Equation. 3 хордасымен абцисса өсінің қиылысу нүктесі ) анықтаудан тұрады және тағы басқа. Итерациялық процесс 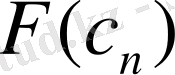Equation. 3 модуль мәні берілген 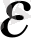Equation. 3 санынв аз болғанға дейін жалғаса береді.

Формуласындағы айырмашылықты санамасақ, екі әдістің де блок - схемасы бірдей болып келеді. Және де блок схемаға жаңа кесінділердің шекарасындағы Ғ(х) мәндерінің есептеу операторларын енгізу қажет.

Көріп отырғанымыздай, қақ бөлу әдісімен хордалар әдісінің алгоритмдері бірдей болып келген. Алайда екіншісінде бірқатар жағдайларда итерациялық процесс тезірек жүреді. Осыған қоса қақ бөлу әдісіндегідей есептің жауабы болады.

Ньютон әдісі

Ал Ньютон әдісінде k - лық итерацияда Equation. 3 болғандағы y=F(x) қисығына жанама жүргізіледі. Мұнда, жанама мен абцисса осімен қиылысу нүктесі ізделінеді. Кесінді 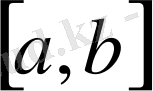Equation. 3 орнына Equation. 3 болатын бастапқы жақындауды тапқан жеткілікті. (5-сурет) .

y=F(x) қисығына Equation. 3 және 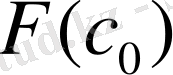Equation. 3 координаттары бар 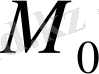Equation. 3 нүктесінде жүргізілген жанаманың теңдеуі мына түрде болып келеді: 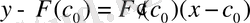Equation. 3

Осыдан келесі Equation. 3 жақындауын табамыз: 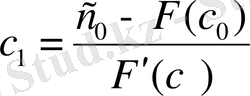Equation. 3 . Сондай етіп 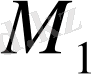Equation. 3, 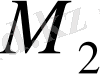Equation. 3 және тағы басқа нүктелеріне жүргізілген жанамалар мен абцисса осімен қиылысу нүктелері болып, келесі жақындаулары табылады. n+1 жақындауының формуласы мынандай болып келеді:

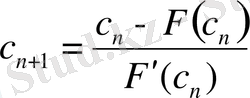Equation. 3 (10)

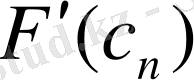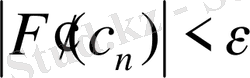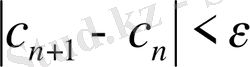нөлге тең болмауы керек. Итерациялық процесстің аяқталуы үшін екі шарттардыңбірі орындалуы керек, не не 7

(10) формуладан Ньютон әдісінде әрбір итерацияда есептеудің көлемі басқа әдістерге қарағанда әлде қайда көп. Осыған қарамастан келісу жылдамдығы үлкенірек болады.

Ньютон әдісінің келісуі мен оның қолдануы жайлы сұрақтарға келсек, мына теореманы айта кеткен жөн болар.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.