ЭЕМ-де сызықтық теңдеулер жүйелерін шешудің сандық және итерациялық әдістері: Гаусс-Зейдель әдісі және бағдарламалық іске асыру


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 29 бет
Таңдаулыға:
КІРІСПЕ
ЭЕМ - нің пайда болуы әртүрлі мамандықтағы мамандардың есептеу техникасын қолдана алуын талап етеді. Жоғары оқу орындарындағы студент-
тердің дайындық деңгейі көтерілді. Студенттер бірінші курстан бастап ЭЕМ -
ді және қарапайым сандық әдістерді қолдануды үйренеді. Сонымен қатар дипломдық, курстық, семестлік жұмыстарды жасағанда да есептеу техникасын қолдану күнделікті жағдайға айналып отыр.
Есептеу техникасы қазіргі уақытта тек инженерлік және экономикалық ғылымдарда ғана емес, сол сияқты медицина, лингвистика, психология және
тағы сол сияқты математикалық емес мамандықтарда да қолданылады. Осыған орай ЭЕМ - нің бүкіләлемдік сипат алғанын көруге болады. ЭЕМ қолданатын мамандардың көптеген категориялары пайда бола бастады.
Осындай негізгі пәндердің бірі есептеу математикасы болып табылады. Ол математикалық әдістерді шешудің сандық әдістерін құру және зерттеу амалдарын оқытады. Есептеу техникасы өзінің негізгі қолданылуын ғылыми зерттеулердегі қиын есептеулерді жүргізуде тапты.
Солай бола тұра есептерді шешуде негізгі қызмет адамға жүктеледі. Ал машина оның құрған программаларын орындайды.
ЭЕМ тек қарапайым операцияларды орындайтындықтан, ол математикалық тұрғыда тұрған есептерді ″түсінбейді″. Бұл жағдайды шешу үшін есепті кейбір есептеу алгоритміне келтіретін сандық әдіс құру керек. Сандық әдістерді есептеу математикасы аймағында жұмыс ісиейтін мамандар құрады.
ЭЕМ - да есеп шығару процесіндегі бір аса қажетті жағдайды айта кеткен жөн. Ол - есепті шығару амалының, сандық әдістің, ЭЕМ моделінің үнемділігі.
ЭЕМ түрлерінің көбеюіне және олардың мүмкіндіктерінің жоғарылауына байланысты математикалық моделдеугежәне сандық әдістерді құруға қызуғышылық артып барады.
Математикалық моедельдеудің көмегімен ғылыми-техникалық есептердің шығарылуы математикалық есептердің шығарылуына келтіріледі. Математикалық есептерді шығару келесі негізгі әдістер қолданылады: графикалық, аналитикалық және сандық.
Графикалық әдістер кей жағдайларда ізделінетін көлемп тізімін бағалау мүмкіндігін береді. Бұл әдістердің негізгі мақсаты - ізделінетін шешімдерді аналитикалық тұрғыда шешу. Мысалы, f(x) =0 теңдеуінің түбірлерін табу үшін y=f(x) функциясының графигі тұрғызылады. Бұл графиктің абцисса осімен қиылысу нүктелері ізделініп отырған түбірлер болып табылады.
Аналитикалық әдістерді қолдану кезінде есептердің шығарылуын формулалардың көмегімен көрсетуге болады. Жеке жағдайда, егер математи-
калық есеп қарапайым алгебралық немесе трансценденттік теңдеулерді, дифференциалдық теңдеулерді шешуден тұрса, онда матеметикалық курсынан белгілі формулаларды қолдануға болады. Өкінішке орай бұл әдіс практика жүзінде өте сирек қолданылады.
Қазіргі кезде қиын математикалық есептерді шығарудағы ең ыңғайлы әдіс сандық әдіс болып табылады.
ЭЕМ - нің пайда болуына байланысты сандық әдістердің күнделікті өмірде қолданылуы да жиілей бастады. Сандық әдістердің есептік мәнін алумен қатар тағы да бір үлкен қасиеті болу керек - есептеу процесінде аса үлкен қателіктер жсамау.
- Есептің берілуі.
n сызықты теңдеулерден тұратын жүйенің жауабын табатын программа
құру.
- Сызықты теңдеулер жүйесі. Негізгі түсініктер.
Сызықтық жүйелер сызықтық теңдецлер жүйесінің шешіміне көптеген практикалық есептер келтіріледі. Сол себептен сызықтық жүйелерді шешу
есептеу математикасының кең таралған және маңызды қызметтерінің бірі деп атаса да болады.
n белгісізі бар n сызықтық алгебралық теңдеулер жүйесін жазайық.
a 11 x i + a 12 x 2 +…+a 1n x n = b 1
a 11 x 1 +a 22 x 2 +…+a 2n x n = b 2
- - - - - - - - - -
a n1 x 1 +a n2 x 2 +…+a nn x n = b n
Бұл жүйенің коэффиценттерін таблица түрінде жазайық:
А=
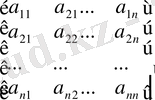
Бұл n2 элементті таблица, n жолдан және n бағыттан тұрады, ол n-ретті квадрат матрица таблица mn элементтерден тұрса, яғни m жолдан және n бағаннан тұрса, онда ол тікбұрышты матрица деп атайды.
А матрицасын қолданып (1) теңдеулер жүйесін матрицалық түрде жазуға болады:
АХ=В,
мұнда Х және В - белгісіздер вектор бағаны және оң жақ бөлігінің вектор баға
 ны.
ны.
Х=
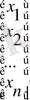 , В=
, В=
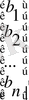
Кей жағдайларда ерекше түрдегі матрицалы теңдеулер жүйесі болады. Осындай матрицалардың кейбір түрлері:
А=
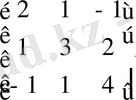 , В=
, В=

С=
 , D=
, D=

E=
 Equation. 3, O=
Equation. 3, O=
 Equation. 3
Equation. 3
Мұнда, А - симметриялы матрица (барлық элементтері бас диагональға симметриялы орналасқан (a ij =a ji ) ) ; B - диагональдің төменгі жағындағы элементтері нольге тең жоғарғы үшбұрышты матрица; С - клеткалы матрица (оның нольге тең емес элементтері бөлек топтар (клетка) құрап тұр) ; D - ленталы матрица (оның нольдік элементтері диагональға параллель ″лента″ құрап тұр) ; Е - бірлік матрица (диагональдардың жеке жағдайы) ; О - нольдік матрица.
n - ретті А матрицасының анықтауышы (детерминаторы) деп D(detA) саны аталады. Ол мынаған тең:
D=
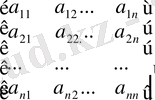 =∑(-1)
k
a
1α
a
2β
… a
nω
(4)
=∑(-1)
k
a
1α
a
2β
… a
nω
(4)
Мұнда, α, β . . . ω - 1, 2, . . . , n номерлерінің барлық мүмкін болатын n! мәндерін қарастырады; К - берілген матрицаның инверсия саны.
D≠0 теңсіздігі сызықтық теңдеулер жүйесін шешудің қажетті және жеткілікті шарты болып табылады. Анықтауышы нольге тең болған жағдайда матрица туынды матрица деп аталады. ; Бұл кезде (1) сызықтық теңдеулер жүйесінің шешімі болмайды немесе оның мәні сансыз көп болады:
a 1 x + b 1 y = c 1 , (5)
a 2 x + b 2 y = c 2 .
Әр теңдеу жазықтықтағы түзуді суреттейді; берілген түзулердің қиылысу нүктелерінің координаттары осы (5) жүйенің шешімі болып келеді.
Екі түзудің жазықтықтағы орналасуының үш мүмкін болатын жағдайын қарастырайық:
- Түзулер қиылысады - (5) жүйенің коэфиценттері пропорционалды емес:(6)
- Түзулер параллель - (5) жүйенің коэффиценттері мына шарттарға бағынады:(7)
- Түзулер сәйкес келеді - барлық коэффиценттері пропорционалды: (8)
(5) жүйесінің D анықтауышын мына түрде жазайық:
D =
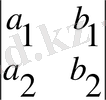
(6) D≠0 шарты орындалса, (5) жүйенің бір ғана шешімі болады. Жүйенің шешімі жоқ немесе сансыз көп болса, (7) немесе (8) қатынастар орын алады. Олардан D=0 аламыз.
Практика жүзінде, әсіресе ЭЕМ - да есептеген кезде, сандарды дөңгелектеген кезде немесе санның кіші разрядтарын алып тастаған кезде анықтауыштың нольге нақты теңдігін алу барлық кезде орындала бермейді. D≈0 болған кезде түзулер бір-біріне параллельге жуық болуы мүмкін (екі теңдеулі жүйе болған кезде) . Бұл түзулердің қиылысу нүктелерінің координаттары жүйенің коэффиценттерінің өзгеруіне жуық болып келеді.
Сол себепті есептеулермен алғашқы мәліметтердің кішкене қателіктері есептің шығарылуында үлкен қателіктерге әкеп соғуы мүмкін. Мұндай теңдеулер жүйесі жаман шартты деп аталады.
2. 1. 2. Сызықтық теңдеулер жүйесін шешу әдістері екі топқа бөлінеді - нақты және итерациялы. Нақты әдістер белгісіздерді табу үшін формуланың соңғы қатынастарын қолданады. Олар есептің мәнін алдын - ала белгілі саны бар операциялар орындалғаннан кейін шығарады. Бұл әдістер салыстырмалы оңай және ыңғайлы, яғни кең көлемді сызықтық жүйелерді шешуге қолайлы.
Сонымен қатар нақты әдістердің бірқатар кемшіліктері бар. Олар ЭЕМ - нің оперативті жадысында матрицаның толығымен сақталуын қажет етеді. Ал n - нің үлкен мәндерінде ол жадыда көп орын алады. Сонымен қатар нақты матрицалар матрицаның құрылымын ескермейді, яғни нольдік элементтері көп болған жағдайда да олар жадыда орын алады және оларға да арифметикалық амалдар орындалады. Нақты әдістердің және бір үлкен кемшіліктерінің бірі - есепті шығару барысында қателіктері топталып жиналуы. Себебі кез-келген этаптағы есептеулерде алдыңғы операциялардың мәні қолданылады. Бұл әсіресе үлкен жүйелер үшін өте қолайсыз. Өйткені операциялардың жалпы саны көп болса, жіберілетін қателіктер де үлкен болып кетеді. Сондықтан нақты әдістерде салыстырмалы кіші (n‹200) жүйелерді есептеуде қолданады.
Итерациялық әдістер - бұл жалғасқан жақындасу әдістері. Бұл әдістерде бір-біріне жақын бір мән - бастапқы жақындасуды беру керек. Бұдан кейін белгілі бір алгоритмнің көмегімен есептеудің бір циклы орындалады. Ол итерация деп аталады. Итерация арқылы жаңа жақындасудың мәнін табады. Итерациялар қажетті дәлдіктей шешім табылғанша орындала береді. Итерациялық әдістермен сызықтық жүйелерді шешу алгоритмі әдетте нақты әдістерге қарағанда күрделірек болып келеді. Есептеулер көлемін алдын-ала анықтау қиын. Сонда да итерациялық әдістер кей жағдайларда қолайлырақ болып келеді. Олар жадыда матрицаның толығымен сақталуын қажет етпейді. Тек n компонентті бірнеше вектор ғана сақталады. Кейде матрица элементтерін мүлдем сақтамаса да болады, сөйтіп қажетті мөлшерде ғана есептейді. Итерациялық әдістерді қолдануда соңғы мәндерінің қателіктері жиналмайды. Итерациялық әдістердің бұл қасиеттері көп теңдеулерді есептегенде өте қолайлы болып келеді. Итерациялық әдістер нақты әдістер арқылы алынған мәндерді дәлдеу үшін де қолданылады.
- Сызықтық алгебраның басқа амалдары
Сызықтық алгебраның сызықтық теңдеулер жүйесін шешуден басқа амалдары бар: анықтауышты, кері матрицаны, матрицаның жеке мәнін есептеу. Тек төменгі ретті анықтауыштар мен анықтауыштардың кейбір ерекше типтері ғана оңай есептеледі. Жеке жағдайда екінші және үшінші ретті анықтауыштар үшін мына есептеулер орындалады:
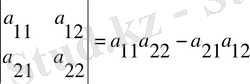

Үшбұрышты матрицаның анықтауышын бас диагональда орналасқа элементтердің көбейтіндісіне тең:
D=a 11 a 22 … a nn . Бұдан бірлік матрицаның анықтауышы бірге, ал нольдік матрицаның анықтауышы нольге тең деген тұжырымға келеміз:
detE = 1, detO = 0.
Жалпы жағдайда анықтауышты есептеу әлдеқайда қиын болып келеді.
n - ретті D анықтауышы мына түрде өрнектеледі:
D =
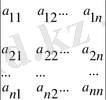 = ∑(-1)
k
a
1α
a
β
… a
nω
= ∑(-1)
k
a
1α
a
β
… a
nω
Осыдан анықтауыш n! қосылғыштарының қосындысына тең екенін көреміз. Ол қосылғыштардың әрқайсысы n элементтер көбейтіндісі болып келеді. Сол себептен n ретті анықтауышты есептеу үшін (n-1) n! көбейту және n!-1 қосу амалдары қажет, яғни арифметикалық операциялардың жалпы саны мынаған тең:
N = n * n! - 1 ≈ n * n!. (9)
Анықтауыштың ретіне байланысты N - нің бағалайық:
ЭЕМ - да мұндай анықтауыштардың есептелу уақытын да табуға болады. ЭЕМ жылдамдығы 1 операциялар секундына деп берілсін.
Сонда 10 - ші ретті анықтауышты есептеу үшін 6 минут, ал 20 - ретті анықтауышты есептеуге 1, 4*10 11 сағат, яғни 5*10 9 тәуліктен астам уақыт керек. Келтірілген мысалдар үнемді сандық әдістерді қолдануды қажет ететінін көрсетеді. Сандық әдістер анықтауыштарды есептеуді тиімді жүргізу мүмкіндігін береді.
Егер көбейтінділері бірге тең болса (АА -1 =A -1 A=E), онда А -1 матрицасы А квадрат матрицасына қатысты кері матрица деп аталады. Сызықтық алгебрада D анықтауышы нольден басқа болатын кез-келген А матрицасының кері матрицасы болатыны дәлелденген.
DetA -1 =1/D
Бастапқы матрицаны мына түрде жазайық:
А =

а ij элементінің миноры деп n - 1 ретті анықтауыш деп аталады.
а ij элементінің Аij алгебралық толықтауышы деп оң таңбамен алынған оның миноры деп аталады.
А
ij
= (-1)
i+j
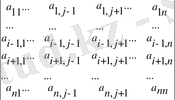
В = А -1 кері матрицасының әрбір b ij (i, j =1, …, n ) элементі A ij алгебралық толықтауышының D анықтауышының мәніне қатынасына тең:
В = А
-1
=
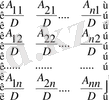 (10)
(10)
Мұнда да жоғарыдағы сияқты кері матрицаны есептеуге қажетті операциялар санын анықтауға болады. Сонымен кері матрицаны есептеуге арналған операциялардың жалпы саны мынаған тең:
N = [(n-1) *(n-1) !-1] *n 2 +n 2 +n*n!-1=n 2 *n!-1 (11)
Сызықтық алгебраның тағы бір маңызды мәснлнсі матрицаның өзіндік мәнін есептеу болып табылады.
2. 2. Итерациялық әдістер.
2. 2. 1. Есептеуді анықтау.
Тура әдістердің көмегімен алынатын мәндердің көптеген қателіктері болады. Кей жағдайларда бұл қателіктер үлкен болып келеді. Сондықтан оларды азайту амалдарын табу керек.
Төменде тура әдістің көмегімен алынған мәндерді нақтылайтын кейбір әдістерді қарастырайық .
- сызықтық теңдеулер жүйесінің шешімін табайық:
a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1
a 11 x 1 +a 2 2x 2 +…+a 2n x n =b 2
- - - - - - - - - -
a n1 x 1 +a n2 x 2 +…+a nn x n =b n
Кез-келген юір тура әдістің көмегімен х 1 (0) , х 2 (0) , . . . , х n (0) белгісіздерінің шешімі табылсын делік. Бұл шешімдерді (1) жүйенің сол жағына қойып, b 1 (i=1, 2, …, n ) бөлек b i (0) мәндерін табамыз:
a 11 x 1 (0) +a 12 x 2 (0) +…+a 1n x n (0) =b 1 (0)
a 11 x 1 (0) +a 22 x 2 (0) +…+a 2n x n (0) =b 2 (0) (12)
- - - - - - - - -
a n1 x 1 (0) +a n2 x 2 (0) +…+a nn x n (0) =b n (0)
Белгілеулерді енгізейік: ε i (0) - белгісіздер шешімдерінің қателіктері, Γ i (0) - байланыссыздықтар, яғни
ε i (0) =x i - x i (0) , Γ i = b i - b i (0) , i = 1, 2, …, n (13)
белгілеулерді ескере отырып (12) жүйенің әр теңдеуін (1) жүйенің сәйкес теңдеулерінен алған кезде келесі жүйені аламыз:
a 11 ε i (0) +a 12 ε 2 (0) +…+a 1n ε n (0) = Γ i (0)
a 11 ε 1 (0) +a 22 ε 2 (0) +…+a 2n ε n (0) = Γ i (0) (14)
- - - - - - - - - -
a n1 ε 1 (0) +a n2 ε 2 (0) +…+a nn ε n (0) = Γ i (0)
Жүйені шеше отырып ε i (0) қателіктерінің мәндерін табамыз. Оларды шешімдерге түзетулер ретінде қолданамыз. Белгісіздердің келесі жуықтаулары мына түрде болады:
x i (1) = x i (0) + ε i (0) , x 2 (0) = x 2 (0) + ε 2 (0) , …, x n (1) = x n (0) + ε n (0)
Осындай әдіспен шешімге жаңа түзетулер және айнымалылардың келесі жуықтауларын табуға болады. Бұл процесс қателіктердің (түзетулердің) барлық келесі мәндері мүмкіндігінше аз болғанға дейін қайталанады.
Қарастырылған шешімді нақтылау процессі сызықтық теңдеулер жүйесін шешудің итерациялық әдісі деп аталады. Келесі жуықтауды, яғни итерацияны табу үшін (14) түріндегі теңдеулер жүйесі шешіледі. Бұл экономикалық алгоритмдерді құру мүмкіндігін береді. Мысалы, Гаусс әдісін қолданғанда есептеулер көлемі қысқарады.
Қарастырылған әдістің, сонымен қатар басқа да әдістердің көмегімен теңдеулер жүйесін шешу келесі амалдарға әкеп соғады. Алғашқы мәліметтер енгізіледі, мысалы, теңдеулер коэффиценті және қателіктердің ескерілмейтін ең үлкен мәні енгізіледі.
Сонымен қатар белгісіздер мәндерінің бастапқы жуықтауларын беру керек. Олар не ЭЕМ - ға енгізіледі, не басқа бір амалмен есептеледі. Содан соң циклдық есептеу процессі құрылады. Мұндағы әр цикл бір итерацияны береді. әрбір итерацияның орындау барысында белгісіздердің жаңа мәндері алынады. Бірінен кейін бірі орындалатын екі итерацияда бұл мәндер кіші болс, процесс тоқтатылады және соңғы итерацияда алынған белгісіздер шешімі шығарылады.
Теңдеулер жүйесін итерациялар әдісімен шешу
- Гаусс - Зейдель әдісі.
Қарапайымдылығымен және оңай программалаулығымен ерекшелене -
тін, кең таралған итерациялық әдістердің бірі болып Гаусс - Гейдель әдісі табылады. Алдымен бұл әдісті жүйені шешу үлгісінде көрсетейік:
a 11 x 1 +a 12 x 2 +a 13 x 3 =b 1
a 21 x 1 +a 22 x 2 +a 23 x 2 =b 2 (15)
a 31 x 1 +a 32 x 2 +a 33 x 3 =b 3
Бұл матрицаның диагональдағы a 11 , a 22, a 33 элементтері нольден бөлек деп алайық. х 1 , x 2 , x 3 белгісіздерін сәйкесінше бірінші, екінші, үшінші теңдеулерден табайық.
х
1
=
 ( b
1
-a
12
x
2
- a
13
x
3
) (16)
( b
1
-a
12
x
2
- a
13
x
3
) (16)
x
2
=
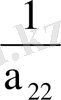 ( b
2
- a
21
x
1
- a
23
x
3
) (17)
( b
2
- a
21
x
1
- a
23
x
3
) (17)
x 3 =
( b 3 - a 31 x 1 - a 32 x 2 ) (18)
Белгісіздердің мәндерінің бастапқы ( нольдік ) жуықтауларын берейік: x 1 = x 1 (0) , x 2 = x 2 (0) , x 3 = x 3 (0) . осы мәндерді (16) теңдеудің оң жағына қойып x 1 үшін жаңа (бірінші) мәнді аламыз.
х
1
(0)
=
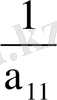 ( b
1
-a
12
x
2
(0)
- a
13
x
3
(0)
)
( b
1
-a
12
x
2
(0)
- a
13
x
3
(0)
)
Бұл мәнді x 1 үшін қолданып x 2 үшін (17) теңдеуден бірінші жуықтау табамыз:
x
2
(1)
=
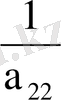 ( b
2
- a
21
x
1
(1)
- a
23
x
3
(0)
)
( b
2
- a
21
x
1
(1)
- a
23
x
3
(0)
)
Сол сияқты алғашқы екі белгісіздің мәндерін қолданып (18) теңдеуден x 3 үшін бірінші жуықтауды табамыз:
x
3
(1)
=
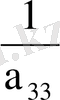 ( b
3
- a
31
x
1
(1)
- a
32
x
2
(1)
)
( b
3
- a
31
x
1
(1)
- a
32
x
2
(1)
)
Осымен (16) - (18) жүйелерді шешудің бірінші итерациясы аяқталады. Бірінші итерацияда алынған мәндерді қолдана отырып екінші итерацияны шығаруға болады және тағы сол сияқты жалғасып жүре береді. k нөмерлі жуықтауды мына түрде жазуға болады:
х
1
(k)
=
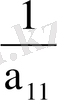 ( b
1
-a
12
x
2
(k-1)
- a
13
x
3
(k-1)
)
( b
1
-a
12
x
2
(k-1)
- a
13
x
3
(k-1)
)
x 2 (k) =
( b 2 - a 21 x 1 (k) - a 23 x 3 (k-1) )
x 3 (k) =
( b 3 - a 31 x 1 (k) - a 32 x 2 (k) )
Итерациялық процесс k - ші итерацияның мәні (k-1) итерацияның мәніне мүмкіндігінше жуықтағанша жалғаса береді.
Мысал. Гаусс - Зейдель әдісі бойынша келесі теңдеулерді жүйесін шешу.
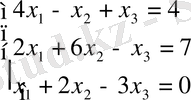
Бұл жүйенің шешімдері х 1 =1, х 2 =1, х 3 =1 болатынын оңай анықтауға болады.
Шешуі: х 1, х 2, х 3 белгісіздерін сәйкесінше бірінші, екінші, үшінші теңдеулерден өрнектейік
х 1 = 1/4 (4+ х 2 - х 3 )
х 2 = 1/6 (7-2х 2 +х 3 )
х 3 =1/3 (x 1 +2х 2 )
Бастапқы жуықтауларды x 1 = x 1 (0) , x 2 = x 2 (0) , x 3 = x 3 (0) деп алайық. Белгісіздердің жаңа жуықтауларын табамыз:
x 1 (1) = 1/4(4+0+0) =1
x 2 (1) = 1/6(7-2*1+0) =5/6
x 3 (1) = 1/3(1+2*5/6) =8/9
Сәйкесінше келесі есептеулерді есептеп аламыз.
x 1 (0) = 1/4(4+5/6-8/9) = 71/72
x 2 (0) =1/6(7-2*71/72+8/9) = 71/72
x 3 (0) = 1/3(71/72+2*71/72) = 71/72
Итерациялық процесті қатар орындалған екі итерацияның белгісіздері -
нің мәндерінің арасындағы жуықтық ең кіші болғанша жалғастыра беруге болады.
Енді n белгісізі бар n сызықтық теңдеулер жүйесін қарастырайық. Оны мына түрде жазайық.
a i1 +…a i, i-1 x i-1 +a ii x i +a i , a i+1 +…a in x n = b i i =1, 2, …, n.
Мұнда барлық диагональдық элементтер нольден өзгеше алайық. Сонда Гаусс - Зейдель әдісіне сәйкес шешімнің k - ші жуықтауын мына түрде көрсетуге болады:
x i (0) = 1/a ii (b i - a i1 x 1 (k) - … -a i, i- 1x i-1 k -a i, i+1 x i+1 (k-1) -… - a in x n (k-1) )
i=1, 2, …, n.
итерациялық процесс k - ші итерацияның мәні (k -1) - ші итерацияның мәніне ең жуық шешімді қабылдағанша жалғаса береді. Бұл шешімдердің жуықтығын олардың δ түрлілігінің максималды абсолют өлшемімен өрнектеуге болады. Сонда итерациялық процесс соңының критериін мына түрде жазуға болады:
δ = max
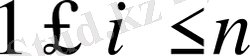 x
i
(k)
- x
i
(k-1)
< ε (20)
x
i
(k)
- x
i
(k-1)
< ε (20)
Бұл абсолютті ауытқу критериі. Итерациялық процесс аяқталуын мына түрде ( x i >> 1 болғанда ) жазуға болады:
max
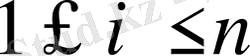
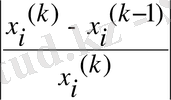 <
ε (21)
<
ε (21)
(20) немесе (21) шарттары орындалған жағдайда Гаусс - Гейдель итерация -
лық процессі жуықтамалары деп аталады.
Итерациялық процесстің жуықтауы үшін диагональді коэффиценттер -
дің модулі басқа теңдеулердің коэффиценттерінің қосындысынан кем болмауы керек:
a
ij
≥
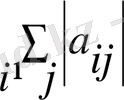 , i=1, 2, …, n. (22)
, i=1, 2, …, n. (22)
Бұл жағдайда ең болмағанда бір теңдеу үшін теңсіздік міндетті түрде орындалу керек.
n сызықтық теңдеулер жүйесін Гаусс - Зейдель әдісімен шешу алгоритмнің блок - схемасы. Блок - схеманы оқу ыңғайлырақ болу үшін кейбір белгілеулердің түсініктемелерін келтіріп қояйық: k - итерациясының реттік
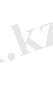 номері; і - берілген циклда есептелетін айнымалының және теңдеудің номері; j - (19) қатынастық оң жағындағы a
ij
x
j
(k)
түріндегі мүшенің номері; итерация (20) шарты орындалған кезде немесе k = - 4 болғанда аяқталады. Соңғы жағдайда итерациялар жуымайды.
номері; і - берілген циклда есептелетін айнымалының және теңдеудің номері; j - (19) қатынастық оң жағындағы a
ij
x
j
(k)
түріндегі мүшенің номері; итерация (20) шарты орындалған кезде немесе k = - 4 болғанда аяқталады. Соңғы жағдайда итерациялар жуымайды.
- Жалпы мағлұматтар.
Прогараммалар Gauss. exe ( cpp, pas ) деп аталады. Программаны функциялау үшін қажетті программалық қамтамалар: OC DOS / WINDOWS. Программалар Turbo Pascal 7. 0, Turbo C++ 3. 0 тілдерінде жазылған.
4. 2. Программаның логикалық құрылымы.
- Программаның аты және комментарий.
- Crt модулін қосу.
- Константалар бөлімі.
4 - 8. Айнымалыларды баяндау бөлімі
4. а - квадрат матрица.
5. х - белгісіздер болатын массив.
b - теңдеулердің бос мүшелері болатын массив.
6. n - теңдеулер саны.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz