Изотермиялық диффузиялық бароэффектіні өлшеу: құрылғы, эксперименттік әдістер және кинетикалық теория


Кіріспе
1. Диффузиялық бароэффект шамасын өлшеуге арналған құрылғының сипаттамасы
Изотермиялық диффузия бароэффектісінің кинетикалық энергиясы
2. 1. Диффузиялық бароэффектінің зерттелу әдісі
2. 2 Диффузиялық бароэффектінің табиғаты
2. 3. Диффузиялық бароэффектінің санақ жүйесіне байланысы
2. 4 Л. Больцман теориясындағы диффузиялық бароэффект
2. 5 Диффузиялық бароэффектінің кинетикалық теориясы
3. Дөңгелек цилиндрлік капиллярда диффузиялық бароэффектті зерттеу
3. 1. Центро масс санақ жүйесіндегі диффузиялық бароэффектіні зерттеу
4. Жазық параллель саңылаудағы изотермиялық диффузиялық бароэффектіні зерттеу
4. 1. Центра масс санақ жүйесіндегі бинарлық қоспалардағы диффузиялық бароэффектіні зерттеу
4. 2 Бароэффект әдісімен бинарлық қоспалардың диффузиялық сырғанау коэффициентін зерттеу
ҚОРЫТЫНДЫ
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР
Кіріспе
Кез келген қайтымсыз процесс тепе-теңсіздік күйлердегі денелерде пайда болады. Егер процестің өтуі уақытқа тәуелді өзгермесе, ол стационар процеске жатады. Ал, керісінше, процестің өтуі уақытқа тәуелді өзгермелі болса - ол стационар емес процесс.
Кез келген оқшауланған термодинамикалық жүйедегі қайтымсыз процестер әрқашан стационар емес болып табылады. Олар жүйенің бастапқы күйі тепе-тең емес жағдайда пайда болып, сол тепе-теңдің жағдайына өту бағытында жүреді. Өз еркіне берілген мұндай жүйелер белгілі бір уақыттан кейін (релаксация уақыты) тепе-теңдік жағдайына келеді.
Газ молекулалары бейберекет қозғала отырып, өзара ретсіз соқтығысады және осы газ орналасқан кеңістікті өз бетімен шарлап жүреді. Кеңістіктің бір жерінен екіншісіне ауысқанда молекулалар өзімен бірге әр түрлі физикалық қасиеттерді, мысалы, массаны, импульстерді, энергияны ала кетеді. Егер кеңістікте қандай да бір физикалық қасиеттің таралуы біртекті болмаса, онда молекулалар бейберекет қозғалысымен осы қасиеттің көп жерінен аз жеріне тасиды. Бұл қасиетті тасу процесі оның таралуы кеңістікте біркелкі болғанша тиылмайды.
Кеңістіктің бір жерінен екіншісіне қандай болса да физикалық қасиеттің молекулалардың жылулық қозғалысымен тасылуы ғылымда тасымалдау құбылыстары деп аталады.
Диффузия. Тепе-теңдік жағдайында фазаның барлық бөлігінде қоспаның әрбір құраушысының тығыздығы бірдей. Тығыздық тепе-теңдік мәнінен ауытқығанда, жүйенің белгілі бір бөлігінде қоспа құраушыларының қозғалысы басталады. Бұл қозғалыс әрбір құраушының тығыздығы барлық көлемде бірдей болатындай бағытта жүреді. Осындай қозғалыспен байланысты зат құраушыларының тасымалдануын диффузия деп түсінеміз.
Зат тасымалдануы концентрация, температура, қысым және сыртқы күштер градиенттері бар ортада жүретін қайтымсыз процесс. Аталған градиенттердің қайсысы қозғаушы күш ретінде болатынына байланысты мұндай тасымалдауларды кәдімгі немесе концентрациялық диффузия, термодиффузия, бародиффузия, сыртқы күштер диффузиясы деп бөлінеді.
1. Диффузиялық бароэффект шамасын өлшеуге арналған құрылғының сипаттамасы
Диффузиялық бароэффектті эксперименттік зерттеу оның шамасы кішкентай болғандықтан, үлкен қиындық тудырады. Сондықтан барлық зерттеулер әдетте төмендетілген қысымдар кезінде жүргізіледі, өйткені қысымның төмендеуімен бароэффект шамасы өседі. Негізгі қиындық қысымның өзгеруін сезгіш индикаторды таңдауымен байланысты. Кейбір зерттеушілер индикатор ретінде мембраналы микромонометрді [2, 6, 7] пайдаланған, оны пайдаланған кезде мембрананың иілулеріне, сонымен қоса мембрананың екі жағындағы гидростатикалық қысымның айырмасына да түзетулер енгізу қажет болды. Диффузиялық бароэффектінің температуралық тәуелділігін зерттеу кезінде осы түзетулерді есепке алу үлкен қиындық көрсетеді.
Құрылғы сызба нұсқасы 1-суретте келтірілген. Капиллярлар жиынының шектеріне арнайы түтікшелер арқылы аз тұтқырлы силиконды май тамшысы бар көлденең түтік 7 жалғанған. Тамшы жағдайы
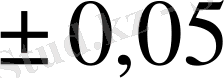 мм дәлдікті жиырма краттық үлкейтуі бар оптикалық түтікпен фиксирленген. Тәжірибе келесі параметрлерге ие болатын құрылғыда жүргізілген: монометрлік түтікше диаметрі 2, 78 мм, ұзындығы -90 мм, кран 5 тесігінің диаметрі 10 мм-ге тең, кран диаметрі 8-6 мм, келтірілетін түтікше диаметрі 4-15 мм. Түгел құрылғы шыныдан пісірілген және 2-суретте бейнеленген, арнайы үс; fps0елшеге бекітілген. Үстелше көлденең негізгі екі аяқпен бекітілген және суреттен көрініп тұрғандай, нүктелерде 3 шаршылы қосылыстар бар. Келесі соңындағы тірек негізге орнықтандырылған және арнайы құралға бекітілген микрометр болып табылады. 6. Серіппелер, сонымен қоса аяқтардың қатты қосылысы бароэффектті өлшеу кезінде көлденең жазықтықта үстелшенің ығысуын болдыртпайды. Өлшеу басына дейін түгел құрылғы ұзақ уақыт бойы зерттелетін газдармен жуылады. Содан кейін микрометрдің көмегімен, монометрлік түтікшенің қатаң көлденеңдігіне қол жеткізуге тырысады, яғни ашық кран 5 кезінде және жабық кран 8 кезінде тамшының тепе-теңдігіне. Диффузиялық ұяшықта белгілі есептеу жүйесі шығарылған кезде, мысалы, орташа сандық жылдамдық жүйесі, бароэффект шамасын өлшейтін құрылғы қосылады, яғни 5 кран жабылып, 8 кран ашылады. Осы кезде тамшы жеңіл газға қарай бағытта тұрақты жылдамдықпен қозғалатын сияқты, өйткені орташа сандық жылдамдықтың жүйесінде артық қысым ауыр компонентасы бар құбырларда пайда болады.
мм дәлдікті жиырма краттық үлкейтуі бар оптикалық түтікпен фиксирленген. Тәжірибе келесі параметрлерге ие болатын құрылғыда жүргізілген: монометрлік түтікше диаметрі 2, 78 мм, ұзындығы -90 мм, кран 5 тесігінің диаметрі 10 мм-ге тең, кран диаметрі 8-6 мм, келтірілетін түтікше диаметрі 4-15 мм. Түгел құрылғы шыныдан пісірілген және 2-суретте бейнеленген, арнайы үс; fps0елшеге бекітілген. Үстелше көлденең негізгі екі аяқпен бекітілген және суреттен көрініп тұрғандай, нүктелерде 3 шаршылы қосылыстар бар. Келесі соңындағы тірек негізге орнықтандырылған және арнайы құралға бекітілген микрометр болып табылады. 6. Серіппелер, сонымен қоса аяқтардың қатты қосылысы бароэффектті өлшеу кезінде көлденең жазықтықта үстелшенің ығысуын болдыртпайды. Өлшеу басына дейін түгел құрылғы ұзақ уақыт бойы зерттелетін газдармен жуылады. Содан кейін микрометрдің көмегімен, монометрлік түтікшенің қатаң көлденеңдігіне қол жеткізуге тырысады, яғни ашық кран 5 кезінде және жабық кран 8 кезінде тамшының тепе-теңдігіне. Диффузиялық ұяшықта белгілі есептеу жүйесі шығарылған кезде, мысалы, орташа сандық жылдамдық жүйесі, бароэффект шамасын өлшейтін құрылғы қосылады, яғни 5 кран жабылып, 8 кран ашылады. Осы кезде тамшы жеңіл газға қарай бағытта тұрақты жылдамдықпен қозғалатын сияқты, өйткені орташа сандық жылдамдықтың жүйесінде артық қысым ауыр компонентасы бар құбырларда пайда болады.
Микрометрдің көмегімен көлбеу бұрышы сырғанау күштеуі қысым күшінен асып кеткенше өзгереді, оның шамасы келесі формуламен анықталады:
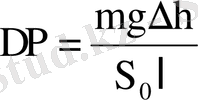 (1. 1)
(1. 1)
мұндағы
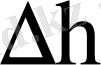 -болат үстелшенің бір шетінің көтерілуі (немесе түсу) биіктігі;
-болат үстелшенің бір шетінің көтерілуі (немесе түсу) биіктігі;
m-тамшы массасы;
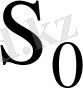 - монометриялық түтікшенің бойлық қимасының ауданы. l- үстелшенің көлбеу бұрышын өзгертетін микрометриялық винттің осінен шариир өсіне дейінгі ара қашықтық
- монометриялық түтікшенің бойлық қимасының ауданы. l- үстелшенің көлбеу бұрышын өзгертетін микрометриялық винттің осінен шариир өсіне дейінгі ара қашықтық
Әрбір температура өлшеу 3-5 рет қайталанды. Силиконды май тамшысын бақылау үздіксіз жүргізілді. Тәжірибе ұзақтығы (көлбеу бұрышының 3-5 есепке алынуымен) 10-нан 14 сағатқа дейін тербелген.
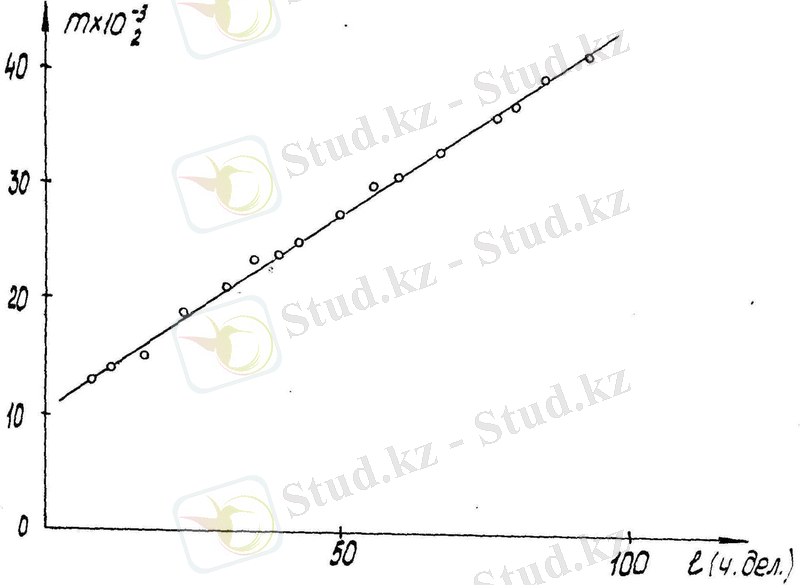
Тамшы массасы тура өлшеумен анықталды. Ол үшін монометрлік түтіктің 7 арнайы кесілген бөлігінде тәжірибеде болған майдың тамшысы енгізілген. Тура өлшеулермен тамшы массасы анықталды, ал оның ұзындығы есептеуіш түтікше көмегімен өлшенген. Алынған мәліметтер ең аз квадраттар әдісімен өңделген және тамшы массасының оның ұзындығынан тәуелділігін байланыстыратын түзу теңдеуі табылған. Одан кейін құрылғыдағы тамшының ұзындығын өлшеп, осы теңдеу бойынша (жұмыстың ыңғайлылығы үшін осы формула бойынша градуирлеу графигі құрылған) тамшы массасы табылады. 3-суретте иллюстрация үшін тамшы массасының оның монометрлік түтікшедегі ұзындығынан тәуелділік графигі келтірілген.
3-сурет. Тамшы массасының ұзындықтан тәуелділік графигі.
Тамшының қозғалысына құрылғы бөлшектерінің әртүрлі конструктивті ерекшеліктері әсер етуі мүмкін: көлденең түтікшенің көлбеуінің мүмкін болуы, оның конустығы, гидростатикалық қысымның мүмкін болу айырымы, мениск температурасының мүмкін болу айырымынан майдың беттік тартылуының айырымы, және т. б. Сондықтан, жоғарыда көрсетілген параметрлермен шарттардан ауытқулардың шығуынан құтылу үшін микроскоптың көмегімен нақтылап барлық ұзындық бойынша бірдей ішкілік диаметрі бар манометрлік түтікті таңдайды. Температуралық әсерлерден құтылу үшін тамшысы бар манометрлік түтікше, сонымен қоса электр пештен газдың шығысы мен кірістері термостаттанған және
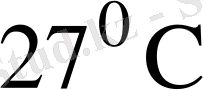 температура кезінде ұстап тұрылған болады. Бақылау тәжірибелерде ауыр және жеңіл компоненттер орындарымен алмастырылады, осы кезде көлбеу бұрышының шамасы өзгермей, көлденеңнен ауытқу бағыты өзгерген. Бұл түтікшенің ерекше конустығының куәсі болады. Сырғанау күштеуін тексеру үшін қажет көлбеу бұрышы, тамшының түтікшеде 7 орналасуынан тәуелді емес, бұл менисктердің беттік керілуінің айырмашылығы орын алмағаны жайлы айтады. Бақылау тәжірибелер сонымен бірге гидростатикалық қысымның мүмкін болу айырымы жайлы күдікпен айырады. Үстелшенің көлденең жағдайдан 0, 05 мм-ге ауытқуы тамшының байқалатын қозғалысын тудырады (m=25, 52 мм және l=2, 78 мм болғанда) -5 минутта 2 бөлік 0, 05
температура кезінде ұстап тұрылған болады. Бақылау тәжірибелерде ауыр және жеңіл компоненттер орындарымен алмастырылады, осы кезде көлбеу бұрышының шамасы өзгермей, көлденеңнен ауытқу бағыты өзгерген. Бұл түтікшенің ерекше конустығының куәсі болады. Сырғанау күштеуін тексеру үшін қажет көлбеу бұрышы, тамшының түтікшеде 7 орналасуынан тәуелді емес, бұл менисктердің беттік керілуінің айырмашылығы орын алмағаны жайлы айтады. Бақылау тәжірибелер сонымен бірге гидростатикалық қысымның мүмкін болу айырымы жайлы күдікпен айырады. Үстелшенің көлденең жағдайдан 0, 05 мм-ге ауытқуы тамшының байқалатын қозғалысын тудырады (m=25, 52 мм және l=2, 78 мм болғанда) -5 минутта 2 бөлік 0, 05
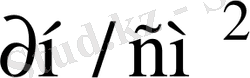
 -ғы қысым айырымына сәйкес келеді. Сонда тамшының орын ауыстыру жылдамдығы көлбеу бұрышының өзгеруінен тәуелсіз болады (яғни, 2-сурет, үстелшенің сол жақ шетінің түсуі немесе көтерілуінен) . Индикатордың қысым өзгеруін сезгіштігі тамшы массасы азайған сайын көбейеді. Бароэффекттінің ең кіші шамасы бөлме температурасына сәйкес келеді, сондықтан біздің тәжірибемізде тамшы ұзындығы 1. 16 мм тең, ал массасы - 15. 88 мг.
-ғы қысым айырымына сәйкес келеді. Сонда тамшының орын ауыстыру жылдамдығы көлбеу бұрышының өзгеруінен тәуелсіз болады (яғни, 2-сурет, үстелшенің сол жақ шетінің түсуі немесе көтерілуінен) . Индикатордың қысым өзгеруін сезгіштігі тамшы массасы азайған сайын көбейеді. Бароэффекттінің ең кіші шамасы бөлме температурасына сәйкес келеді, сондықтан біздің тәжірибемізде тамшы ұзындығы 1. 16 мм тең, ал массасы - 15. 88 мг.
Диффузиялық ұяшық пен құбырлардан газдардың кірісі мен шығысының арасында температуралық айырым құрылғандықтан, зерттелетін бинарлы қоспа үшін формула бойынша термодиффузиялық бароэффекттің әсері анықталған:
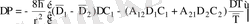 (1. 2)
(1. 2)
мұндағы
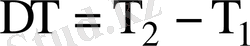 ;
;
r-келтірілген түтікшелер радиусы, 2 мм-ге тең. .
Диффузиялық бароэффекттің газдардың әртүрлі жүйелері үшін бақылау өлшеулері, сондай-ақ ИПЕ (сыйымдылықтың өсуін өлшегіш) қондырғысына қосылған МБС-7 дифференциалды сыйымдылықты электронды микромонометрмен жүргізілген. Алынатын қысымның айырымдарын тіркегіш 0, 006 mV бағалау бөлімі бар шамды электронды микровольтметр болып табылады. Температураның тербелістерінің әсерінен құтылу үшін, микромонометрдің мембраналары ауалық термостатта орнатылған.
Электронды микромонометрдің градуирлеуін келесі екі әдіспен жүзеге асырылды: І-таза газ ағымын пульсирлемейтін гидростатикалық қысымның өзгеруі бойынша, мұнда газдың шығу деңгейінің h әрбір белгілі жағдайына
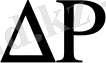 -ның белгілі мәні сәйкес келеді, ол келесі формуламен өрнектеледі:
-ның белгілі мәні сәйкес келеді, ол келесі формуламен өрнектеледі:
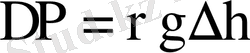 (1. 3)
(1. 3)
мұндағы
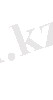
 -градуирлеу температурасы кезінде газ тығыздығы
-градуирлеу температурасы кезінде газ тығыздығы
g- ауырлық күшінің үдеуі
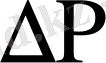 -ның тіркегіштің көрсеткішінен тәуелсілігін жазып, градуирлеу (үлгілеу) графигі құрылған болатын (градуирлеу газ ретінде таза гелий қолданылды) градуирлеудің екінші әдісінде микромонометрдің шығысына параллель, диффузиялық бароэффектіні өлшеу үшін қызмет атқаратын құрылғы қосылды. Көлденең түтікшенің көлбеу бұрышын өзгертумен қысымның
-ның тіркегіштің көрсеткішінен тәуелсілігін жазып, градуирлеу (үлгілеу) графигі құрылған болатын (градуирлеу газ ретінде таза гелий қолданылды) градуирлеудің екінші әдісінде микромонометрдің шығысына параллель, диффузиялық бароэффектіні өлшеу үшін қызмет атқаратын құрылғы қосылды. Көлденең түтікшенің көлбеу бұрышын өзгертумен қысымның
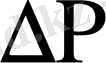 белгілі айырымын тудыра тіркегіштің көрсеткішін жазамыз. Градуирлеудің бұл тәсілі
белгілі айырымын тудыра тіркегіштің көрсеткішін жазамыз. Градуирлеудің бұл тәсілі
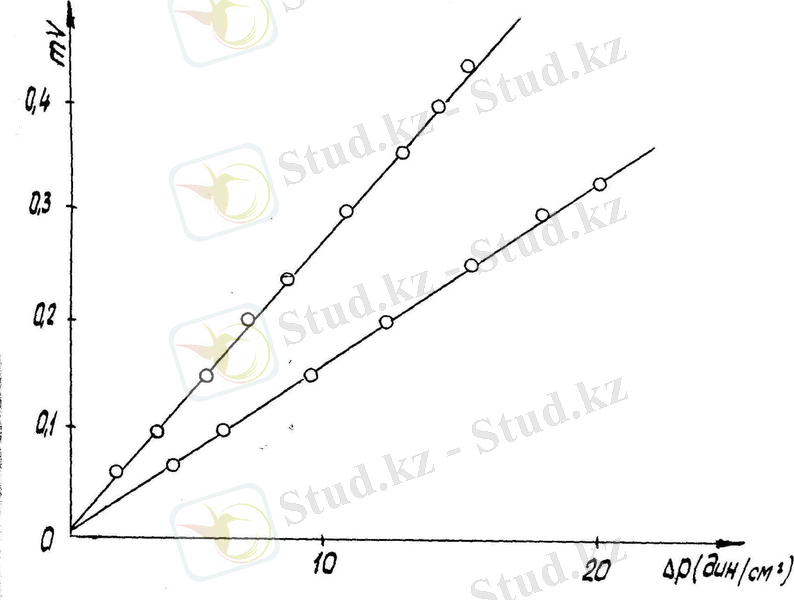
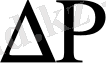 әсерімен мембрананың иілуін тікелей өлшеуге рұқсат етеді. Екінші әдіспен градуирлеу қисығы (мембрананың иілуі есепке алынған) 4-суретте келтірілген. Градуирлеудің максимал қателігі 2%-тен аспайды.
әсерімен мембрананың иілуін тікелей өлшеуге рұқсат етеді. Екінші әдіспен градуирлеу қисығы (мембрананың иілуі есепке алынған) 4-суретте келтірілген. Градуирлеудің максимал қателігі 2%-тен аспайды.
4-сурет. Электронды микромонометрдің МБС -7 градуирлеу графигі.
Жоғарыда көрсетілген екі әдістің сезгіштігінің әртүрлі шектерінде жүргізілген МБС-7 электронды микромонометрдің градуировкасы сәйкес келеді. Бұл, көлденең түтікте силиконды май тамшысы бар монометрлік құрылғы жұмысының сенімділігі жайлы айтады.
Изотермиялық диффузия бароэффектісінің кинетикалық энергиясы
2. 1. Диффузиялық бароэффектінің зерттелу әдісі
Өзара диффузиялық газдардың бароэффектісінің бар болуы Больцман және Максвелл [1] кезеңінде айтылған. Бірақ, диффундирлейтін газбен екі көлемді байланыстыратын каппиляр түбіне өте аз қысымның түсуіне байланысты, диффузиялық бароэффект эксперименталды түрде кейіннен зерттеле басталды. Ауада цилиндрлік капилляр арқылы судың стационарлы диффузиясын зертегенде, Крамерс және Кистемакер [2] сандық өлшемді диффузиялық бароэффектіні ойлап шығарды.
Миллер және Кармен [3, 4] тәжірибелерінде Лошмид ұяшығы қолданылды. Ол гетеродиффузия (
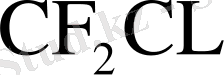 және сутегі ) коэфициентімен көп ерекшеленетін газдармен толтырылған екі шыны цилиндрден тұрады. Шекара бөлімінің қозғалысының индикаторы ретінде аммоний хлорының түтіні алынды. Камераларды біріктіргеннен кейін төменгі цилиндрде сутегі жылдам диффундиурленеді. Онда қысымы көтеріліп, нәтежиесінде қосымша ағын пайда болады да, өзімен қоса түтіннің бөлшегін жұтып алады. Түтін бөлшегінің қозғалысы диффундирлейтін газ қоспасында ақиқат индикатор ретінде қызмет атқара алмайды және бөлшек алмасуының жылдамдығы оның диаметрі мен молекулалардың жолының еркін ұзындығының қатынасына тәуелді. Тәжірибе шарттарында мүмкін болмайтын, бөлшекті тұндыруда міндетті түрде түзетулер енгізу керек.
және сутегі ) коэфициентімен көп ерекшеленетін газдармен толтырылған екі шыны цилиндрден тұрады. Шекара бөлімінің қозғалысының индикаторы ретінде аммоний хлорының түтіні алынды. Камераларды біріктіргеннен кейін төменгі цилиндрде сутегі жылдам диффундиурленеді. Онда қысымы көтеріліп, нәтежиесінде қосымша ағын пайда болады да, өзімен қоса түтіннің бөлшегін жұтып алады. Түтін бөлшегінің қозғалысы диффундирлейтін газ қоспасында ақиқат индикатор ретінде қызмет атқара алмайды және бөлшек алмасуының жылдамдығы оның диаметрі мен молекулалардың жолының еркін ұзындығының қатынасына тәуелді. Тәжірибе шарттарында мүмкін болмайтын, бөлшекті тұндыруда міндетті түрде түзетулер енгізу керек.
Газдардағы диффузиялық бароэффекті қатты денелердегі Киркендала эффектісінің аналогы есебінде Маккарти және Масонмен бірге зерттелді [5] . Қысым төмендеуін тіркеу үшін алғаш рет сапфирлі шаригі бар горизонталды таяқша қолданылды. Ол силиконды маймен жағылған газдар диффузиясында капилляр арқылы индикатор ауыр газдардан жеңілге қарасты қозғалады және ығысу жылдамдығы арқылы ыдыстағы газ көлемінің жылдамдығы және әртүрлі қысымдағы шамалары анықталады. Осыдан, индикатордың алмасу жылдамдығының абсолютті қысымнан және капилляр диаметрінен тәуелділігі анықталды. Алынған бірнеше тәжірибелер нәтижелерінің айырмашылығы және поршендік-тамшылардың екі жағындағы беттік керілу эффектісі әртүрлі. Алғаш рет бароэффект әдісімен өзара диффузиялық коэффициенті өлшенді.
Зерттеу нәтижесінде Маккарти және Масон мынадай қорытынды жасады: Даркеннің феноменологиялық теориясы газдардағы аналогиялық эффектіні сипаттауда қолданылмайды, ал қатаң кинетикалық теория қарастырып отырған эффектіні сапалы түрде сипаттауға мүмкіндік береді. Маккарти және Масон эффектіні кинетикалық сипаттауда шексіз ортадағы диффузиялық ағын мәнін қолданады, яғни газдардың өзара әсерлесу салдарын пренебрленген сондықтан Kn < 1 болғанда бұл әсер өте аз болады.
Диффузияланатын газ қоспаларында диффузиялардың бароэффектісі суспенциялық бөлшек қозғалысымен тығыз байланысты. Теория жүзінде бұл қозғалыс тәжірибедегі сияқты төменгі және жоғарғы сандық қысымда зерттелді. Зерттеу нәтижесінен кейбір жағдайда өлшенген бөлшектің қозғалысы төменгі қысым да жоғарғы қысым қозғалысының бағытына кері болады. Вальдман мен Шмидтың [6] жұмыстарының мақсаты - капилляр арқылы өтетін диффузия кезінде қысым төмендегенде таңбаның ауысуын түсіндіру. Диффузиялық бароэффект манометрмен өлшенеді: ол силиконды маймен толтырылған (горизонталь иіннің барлығы) . Микроскоптың көмегімен есептеулер жүргізілді. Көлемдері шыны таяқшадан жасалған. Қатаң изометрияны жоқ деп санап, екі капиллярда 20
 С температурада зерттеу жүргізілді.
С температурада зерттеу жүргізілді.
Жұмыста диффузиялық бароэффекттің уақытқа тәуелділігі және оның абсолют қысымына тәуелділігі зерттелді. Бұдан, тәжірибенің нәтижесі теориялық формулаға сәйкес келмейді, себебі оның негізі диффузиялық сырғанау коэффициенті болды. Вальдман мен Шмид диффузиялық бароэффектіні өлшегенде силиконды маймен толтырылған монометрді қолданды.
Суетин П. Е. бастаған топ диффузиялық бароэффектіні түрлі жағынан зерттеуде үлкен үлес қосты. [7] . Диффузиялық бароэффектіні зертеуде жоғары сезгіш сыйымдылықты диффузиялық микроманометр құрастырылды. Онда негізгі элемент болып бериллий қоладан жасалған, диаметрі 64мм., қалыңдығы 0, 1 мм., болатын, вертикаль орналасқан екі гофрирлы мембрана қызмет етеді. Өлшеу кезінде қысымның төмендеу әсерінен мембраналардың біреуі ауысады да, араларындағы сыйымдылығын өзгерте отырып, екінші өлшеуіш - құрал ретінде өсіру сыйымдылығы тіркелді. Гидростатикалық қысым үшін диффузияланатын газдардың әртүрлі жазықтықта болуы, капилляр таяқша, камералардағы қысымды теңестіру және микроманометрлер бір горизонталь жазықтықта құралған. Температура айырымын алып тастау мақсатында камералар массивты орындалады және барлық құрылғы аллюминдік жәшікте орналастырады. Ал, ол ауа толтырылған термостатпен жалғанған. Құрылғының эксперименттік сипаттамадағы және өлшеу әдістемесі [7] жұмыста келтірілген. Осы жерде бароэффектіні бинарлық қоспа үшін уақытқа тәуелділігін зертелді:
 атмосфералық қысымда және 20
атмосфералық қысымда және 20
 С температурада.
С температурада.
Бароэффектінің максималды мағынасы есептеулермен берілген. Осыдан өзара диффузиялық коэффициенті өлшеулерден және тәжірибиелік шарты үшін есептелген формуладан алынды:
(2. 1)
T және Р- тәжірибенің температурасы мен қысымы.
Диффузиялық сырғанау кең диапазонды атмосфералық қысымнан қысымға дейінгі бароэффект әдісімен зерттеуде газ қоспасының молекулалық ағысына сәйкес келетін :
 алынды, бұдан Кнудсеннің сырғанау диффузия коэффициентінің мағынасы нөлге жақын,
алынды, бұдан Кнудсеннің сырғанау диффузия коэффициентінің мағынасы нөлге жақын,
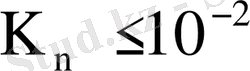 және 100 мм. сын. бағ. қысымда және одан аз кезде болады деген қорытынды шықты. Волобуев және Суетиннің [8] жұмысында қатаң кинетикалық теория әдісімен алынған бароэффекттің максималды мәнінің формуласы тексерілді. Алынған формула, авторларды айтуынша, қиын интегралдарға жатпайды және диффузия бароэффектісінің шамасының капилляр ұзындығына тәуелсіз екені анықталды.
және 100 мм. сын. бағ. қысымда және одан аз кезде болады деген қорытынды шықты. Волобуев және Суетиннің [8] жұмысында қатаң кинетикалық теория әдісімен алынған бароэффекттің максималды мәнінің формуласы тексерілді. Алынған формула, авторларды айтуынша, қиын интегралдарға жатпайды және диффузия бароэффектісінің шамасының капилляр ұзындығына тәуелсіз екені анықталды.
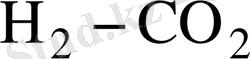 бинарлық қоспалары үшін масса және эффективтік диаметрлер бірдей екені және бароэффекттің жоқтығы анықталды. [9] жұмыста бароэффект әдісімен өлшенген бірнеше бинарлық жүйелердегі өзара диффузия коэффициентінің өлшеу нәтижесі көрсетілген. Мұндай өлшемдерді атмосфералық қысымда және жоғары қабырғалы құбылыстарда жасау қажет, П. Е. Суетин және оның әріптестері шекаралық эффектті инертті газдардың бөлінуі кезінде шыны капилляр жинағында бароэффект шамасының капилляр санына тәуелділігін және жоғары қысымдағы бароэффект шамасын өлшеді. Бірінші жуықтауда толық момент әдісімен келесі иттерациалық мәндерінен жазық каналды бароэффекті зертелді. Бұл зерттеулердің барлығы бөлме температурасында және орташа сандық санақ жүйесінде жасалды. Диффузиялық бароэффектіні өлшеуде мембрана иілуі ескеріледі, бірақ мембрананың екі жағындағы гидростатикалық қысымға түзету енгізілгені немесе енгізілмегені түсініксіз болып қалады. Егерде мембарана диаметрі d = 64 мм болатынын ескерсек, онда бұл эффекттің әсері нақты болады.
бинарлық қоспалары үшін масса және эффективтік диаметрлер бірдей екені және бароэффекттің жоқтығы анықталды. [9] жұмыста бароэффект әдісімен өлшенген бірнеше бинарлық жүйелердегі өзара диффузия коэффициентінің өлшеу нәтижесі көрсетілген. Мұндай өлшемдерді атмосфералық қысымда және жоғары қабырғалы құбылыстарда жасау қажет, П. Е. Суетин және оның әріптестері шекаралық эффектті инертті газдардың бөлінуі кезінде шыны капилляр жинағында бароэффект шамасының капилляр санына тәуелділігін және жоғары қысымдағы бароэффект шамасын өлшеді. Бірінші жуықтауда толық момент әдісімен келесі иттерациалық мәндерінен жазық каналды бароэффекті зертелді. Бұл зерттеулердің барлығы бөлме температурасында және орташа сандық санақ жүйесінде жасалды. Диффузиялық бароэффектіні өлшеуде мембрана иілуі ескеріледі, бірақ мембрананың екі жағындағы гидростатикалық қысымға түзету енгізілгені немесе енгізілмегені түсініксіз болып қалады. Егерде мембарана диаметрі d = 64 мм болатынын ескерсек, онда бұл эффекттің әсері нақты болады.
[28] жұмыста Л. С. Котоусов мына формулаға экспериментальды тексеру жүргізді:
(2. 2)
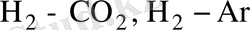 қоспалары үшін орташа сандық санақ жүйесінде бөлме температурасында жасалды. Бұл өлшеулер біздің ойымызша жартылай сандық сипаттамаға ие. Бароэффектіні төмен қысымдар үшін зерттеу [10] жұмыста көрсетілген. Мақсаты:Сырғанау диффузиясының біртексіз газ қоспасының ағысына әсерін анықтау. Диффузиялық бароэффектіні алғашқы рет әскери дәрігер Ф. В. Шмилдовский газдардың өзара диффузиясын саңылаудан өтуі кезінде байқаған, қысымның төмендеуін диффузиялық жылдамдық компоненттерінің бірдей еместігін, деп түсіндіре отырып, автор бұл эффект ауа ылғалдылығын өлшеу үшін қолданады. Бірақ, ол бароэффектінің өлшенген шамасын ауадағы будың серпімділігі мен байланыстыра алмады. Диффузиялық бароэффектінің техникада қолданылуы Б. В. Дерягиннің жетекшілігімен шешілді. Диффузиялық бароэффектінің үш қоспалы баллансты газдардың компоненттерінің ауысуына ықпалын зерттеу Н. Д. Косов пен З. И. Ловосада жұмыстарында көрсетілген. Бароэффектіден алынған гидродинамикалық ауысу, молекулалық сияқты қатарларға ие. Олар компонентті қоспаның, Тур [12] “эффекттісінің” пайда болуын бароэффект әсерінен деп түсіндірді.
қоспалары үшін орташа сандық санақ жүйесінде бөлме температурасында жасалды. Бұл өлшеулер біздің ойымызша жартылай сандық сипаттамаға ие. Бароэффектіні төмен қысымдар үшін зерттеу [10] жұмыста көрсетілген. Мақсаты:Сырғанау диффузиясының біртексіз газ қоспасының ағысына әсерін анықтау. Диффузиялық бароэффектіні алғашқы рет әскери дәрігер Ф. В. Шмилдовский газдардың өзара диффузиясын саңылаудан өтуі кезінде байқаған, қысымның төмендеуін диффузиялық жылдамдық компоненттерінің бірдей еместігін, деп түсіндіре отырып, автор бұл эффект ауа ылғалдылығын өлшеу үшін қолданады. Бірақ, ол бароэффектінің өлшенген шамасын ауадағы будың серпімділігі мен байланыстыра алмады. Диффузиялық бароэффектінің техникада қолданылуы Б. В. Дерягиннің жетекшілігімен шешілді. Диффузиялық бароэффектінің үш қоспалы баллансты газдардың компоненттерінің ауысуына ықпалын зерттеу Н. Д. Косов пен З. И. Ловосада жұмыстарында көрсетілген. Бароэффектіден алынған гидродинамикалық ауысу, молекулалық сияқты қатарларға ие. Олар компонентті қоспаның, Тур [12] “эффекттісінің” пайда болуын бароэффект әсерінен деп түсіндірді.
Компонентті жүйеде диффузиялық бароэффектінің концентрациялық тәуелділігі [12] жұмыстарда көрсетілген.
Бароэффектінің эксперименталды мәні бинарлық қоспаның
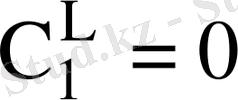 және
және
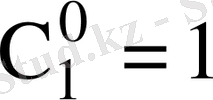 соңғы концентрациялары үшін сәйкессіздігін автор теорияда өзара диффузия коэффициентінің дәл өлшенбеуінен деп түсіндіреді.
соңғы концентрациялары үшін сәйкессіздігін автор теорияда өзара диффузия коэффициентінің дәл өлшенбеуінен деп түсіндіреді.
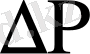 -ның қысымнан тәуелділігі зерттеліп,
-ның қысымнан тәуелділігі зерттеліп,
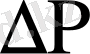 -ның қысымнан кері пропорционалдылығы 140-220 мм сынап бағанасы аралығында бақыланды. Бұл шамадан төмен қарай
-ның қысымнан кері пропорционалдылығы 140-220 мм сынап бағанасы аралығында бақыланды. Бұл шамадан төмен қарай
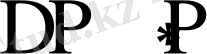 туындысының экспоненциалдық құлауы байқалады.
туындысының экспоненциалдық құлауы байқалады.
Бароэффектіні есептеуде, диффузиялық капиллярдағы айналмалы қиылысу радиусы r пуазейлдік ағысында орынға ие болады деп есептеді. Онда көп компонентті қоспа үшін диффузиялық бароэффекттінің диференциалды теңдеуін алуға болады.
(2. 3)
Мұндағы,
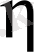 -қарастырылып отырған капилляр ағысындағы динамикалық қоспаның тұтқырлығы;
-қарастырылып отырған капилляр ағысындағы динамикалық қоспаның тұтқырлығы;
 - i және n компоненттерінің ақиқат диффузиялық коэффициенті.
- i және n компоненттерінің ақиқат диффузиялық коэффициенті.
[12] жұмыстан диффузиялық бароэффект үшін капиллярдағы концентрацияның сызықтық таралу ұзындығы L арқылы ақиқат диффузия коэффициентінің өрнегі алынды. Формулаларды эксперименталды мәндермен салыстыру жүргізілді. [13] жұмыста өзара диффузия коэффициентін қолданып үшкомпонентті жүйеде қысымның төмендеуінің есептеу өрнегі берілген.
Диффузиялық бароэффектіні түрлендірудің механизмін диффузиялық бароэффект шамасы және диффузиялық коэффициентке санақ жүйесіне және әртүрлі термодинамикалық параметрлеріне тәуелділігі [15-17, 24-25] жұмыстарда көрсетілген.
2. 2 Диффузиялық бароэффектінің табиғаты
[28] жұмыста көрсетілгендей диффузиялық бароэффект табиғатына екі түрлі көзқарас бар. Біріншісі, [3, 4, 5] келісетін болсақ, бароэффектінің туындауы болып диффузиялық жылдамдықтың компоненттерінің әртүрлілігі жатады. Яғни, кері нәтижелі ағынды мынадай жылдамдықпен тудырады:
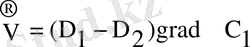 (2. 4)
(2. 4)
мұндағы,
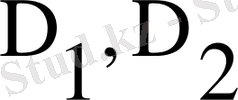 -бірінші және екінші диффузиялық газдардың “ішкі” коэффициенті;
-бірінші және екінші диффузиялық газдардың “ішкі” коэффициенті;
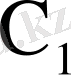 -жеңіл компоненттердің салысырмалы көлемдік концентрациясы.
-жеңіл компоненттердің салысырмалы көлемдік концентрациясы.
Бұл жұмыстарда диффузиялық бароэффект қатты денедегі Киркендалла эффектісінің аналогі ретінде қарастырылады. Эксперимент нәтижесі жай феноменологиялық теория мен газдардың қатаң кинетикалық теориясымен айтылады.
Қысымның төмендеу шамасы тамшы поршенінің қозғалысымен және тамшы жылдамдығы нөлге тең жағдайда анықталады.
(2. 5)
мұндағы
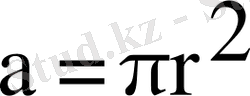 -капиллярдың қиылысу ауданы;
-капиллярдың қиылысу ауданы;
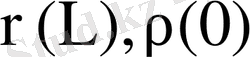 -капиллярдың соңғы компонентінің парциалды тығыздығы, мына шартта, егер
-капиллярдың соңғы компонентінің парциалды тығыздығы, мына шартта, егер
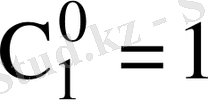 және
және
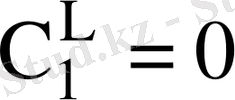 , онда таза массаның компонентін аламыз.
, онда таза массаның компонентін аламыз.
[2. 4] теңдеу өзара диффузияның мейерлік көрінісін білдіреді де, былай анықталады:
(2. 6)
Л. С. Котоусов (2. 6) формуламен анықталатын өзара диффузиялық коэффициент эксперименталды мағынасымен қанағаттандырмайды, - деп есептейді, және өте жылдам
 коэффициентінің концентрацияға тәуелділігін білдіреді.
коэффициентінің концентрацияға тәуелділігін білдіреді.
Екінші көзқарастағылар былай дейді: Бастапқы уақыт моментінде, яғни
 болғанда, орташамассалық жылдамдықта нөлге тең. Бұл екі компоненттің молекулярлық ағынының айырмашылығының бар екендігіне әкеп соқтырады, яғни диффузиялық бароэффектінің енгізілгеніне де көп зерттеушілер осы қағиданы ұстанды. [2, 8, 9] жұмыстарда квазистационар жағдайдағы диффузиялық бароэффект шамаларының формулалары келтірілген. Онда ортақ молекулалардың ауысуы болмайды.
болғанда, орташамассалық жылдамдықта нөлге тең. Бұл екі компоненттің молекулярлық ағынының айырмашылығының бар екендігіне әкеп соқтырады, яғни диффузиялық бароэффектінің енгізілгеніне де көп зерттеушілер осы қағиданы ұстанды. [2, 8, 9] жұмыстарда квазистационар жағдайдағы диффузиялық бароэффект шамаларының формулалары келтірілген. Онда ортақ молекулалардың ауысуы болмайды.
Тұйық диффузиялық аспаптарда, біруақытта концентрация мен қысым градиенттері болатын және орташа жылдамдық компоненттерінің әртүрлілігі мынадай түрде жазылады :
(2. 7)
мұндағы,
 және
және
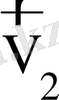 - бірінші, екінші сортты газдардың орташа жылдамдығы.
- бірінші, екінші сортты газдардың орташа жылдамдығы.
[2. 7] формуладан молекула ағынының векторының тығыздығы мынадай түрде алынады:
Equation. 3 (2. 8)
Equation. 3 (2. 9)
мұндағы,
- қоспа молекулаларының орташа массасы.
Егерде қоспаның диффузиялық сырғанауының жылдамдығы қабырғада нөлге тең болса, онда гидродинамикалық ағын Пуазейлдің теңдеуімен анықталады:
(2. 10)
мұндағы
-гидродинамикалық ағынның жылдамдығы.
Квазистационарлы жағдайдағы шартты қолдана отырып және бародиффузиялық ауысуды оның аздығымен [2. 7, 2. 8, 2. 9] теңдеулерінен анықталды:
(2. 11)
(2. 11) -теңдеуді капилляр ұзындығы бойынша интегралдасақ, бароэффект шамасына байланысты диффузиялық сырғанау коэффициентін есепке алмай бароэффект шамасының теңдеуін аламыз:
(2. 12)
мұндағы,
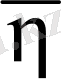 - қоспаның капилляр ұзындығы бойынша орташаланған тұтқырлық коэффициенті.
- қоспаның капилляр ұзындығы бойынша орташаланған тұтқырлық коэффициенті.
-капилляр соңындағы бірінші компоненттің концентрациясы.
Шарт бойынша, капилляр соңында таза газдар болады, яғни
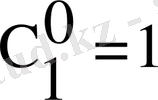 ,
,
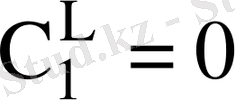 болғанда (1. 12) -теңдеуі мына түрде жазылады:
болғанда (1. 12) -теңдеуі мына түрде жазылады:
(2. 13)
(2. 13) теңдеуден алынатын диффузиялық бароэффект шамалары тәжірибеге сәйкес келмейді және оларды екі есе үлкейтеді. Мұндай сәйкеспеушілік кейбір автор жұмыстарында [2, 8, 9, 17, 18] диффузиялық сырғанау деп аталатын көрініспен түсіндіріледі. Гред әдісінің “13-моменттік” жуықтауын қолдансақ, сырғанау жылдамдығы мына түрде жазылады:
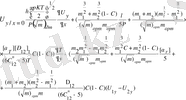
(2. 14)
Мұндағы,
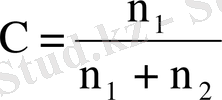 - молекуланың 1 компонентінің қоспадағы салыстырмалы концентрациясы.
- молекуланың 1 компонентінің қоспадағы салыстырмалы концентрациясы.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz