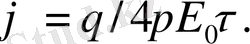Электростатика: электр зарядтарының қасиеттері, Кулон заңы, өріс пен потенциал, диэлектриктер, өткізгіштер және конденсаторлар


Электростатика.
Электр заряды және оның қасиеттері.
Электр заряды дегеніміз - денелердің немесе бөлшектердің электромагниттик әсерлесу қасиетін сипаттайтын шама.
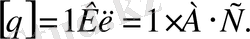
1 Кл дегеніміз - өткізгіштің көлденең қимасы арқылы 1с ішінде 1А ток күшіне тең болатындай электр зарядының шамасы.
Элементар электр заряды
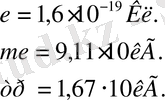
Элементар электр зарядының негізгі қасиеттері:
- 2 түрде - оң және теріс
Әр аттас зарядтар тартылады
біртектес зарядтар тебіледі.
- Электр зарядыинварианттыяғни оның шамасы санақ жүйесіне байланысты болмайды.
- Электр зарядыдискренттіяғни кез келген дененің заряды е-н бүтін санын құрайды, е жарылысы болуы мүмкін емес.
- Электр зарядыактивтіяғни кез келген жүйенің заряды сол жүйеге кіретін зарядтардың қосындысына тең.
- Электр заряды сақталу заңына бағынады. Зарядтың сақталу заңы: кез келген тұйық жүйенің электр зарядтарының алгебралық қосындысы сол жүйенің ішінде қандай процестер болып жатса да өзгеріссіз қалады.
Тұйық жүйе дегеніміз (электростатикада) - сыртқы денелермен заряд алмаспайтын жүйе.
Кулан заңы.
Қозғалмайтын 2 нүктелік зарядтардың әсерлесу күші q 1 , q 2 - тура пропорционал, ал олардың ара қашықтығының квадратына кері пропорционал.
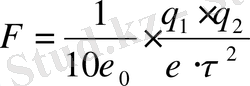 Е
-
ортаның диэлектр сиымдылығы.
Е
-
ортаның диэлектр сиымдылығы.
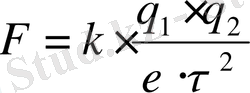
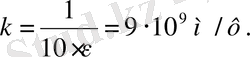
Ортаның диэлектрик сиымдылығы - ортаның зарядтарының арасындағы әсерлесу күші вакуумдағы әсерлесу күшінен қанша есе аз екенін көрсететін шама.
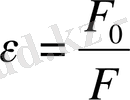
Электростатикалық өрістің кернеулігі
Электростатикалық өріс дегеніміз - қозғалмайтын электр зарядтарын тудыратын өріс.
Электростатикалық өрісті сипаттайтын шама электр өрісінің кернеулігі - бірлік оң зарядта әсер ететін күш пен анықталатын физикалық шама
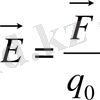
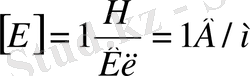
Электр өрісінің кернеулігі - электр өрісінің күштік (векторлық) сипаттамасы.
1Н/Кл дегеніміз - нүктелік 1 Кл зарядқа 1 Н күш әсер ететіндей өрістің кернеулігі.
Вакуумдегі нүктелік зарядтың өріс кернеулігі.
модуль векторлық
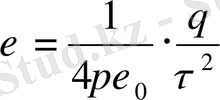
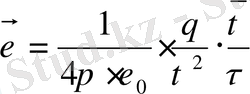
 - өрістің қарастырылып отырған өрістің нүктенің зарядты қосатын радиус вектор.
- өрістің қарастырылып отырған өрістің нүктенің зарядты қосатын радиус вектор.
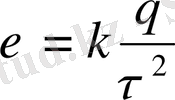 скалярлық түрде
скалярлық түрде
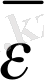 векторының бағыты оң зарядқа әсер ететін күштің бағытымен бағыттас болады.
векторының бағыты оң зарядқа әсер ететін күштің бағытымен бағыттас болады.
Егер өріс оң зарядтан радиус вектор бағытымен сол зарядтан сыртқы кеңістікке кетіп бара жатқандай болады.
егер өріс нүктелік зарядтан пайда болса онда кернеулік сызықтары сол зарядтан (оң болса) шығып жатқан болады, (теріс болса) кіріп жатқандай болады.

 ағыны.
ағыны.
Егер кернеулік сызықтарының көмегімен электр өрісінің кернеулігінің бағыты ғана емес сонымен қатар мәнін де сипаттайтын болсақ, онда ол сызықтарды белгілі бір сызықтар жиі орналасады.
Кернеулік сызықтарының бірлік ауданды қиып өтетін саны модулі бойынша кернеулік модулінің шамасына тең болады.
dS ауданды қиып өтетін сызықтар саны былай анықталады:
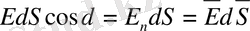
dS
 Equation. 3
Equation. 3
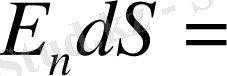 кернеулік векторының ағыны.
кернеулік векторының ағыны.
d
 Equation. 3
Equation. 3
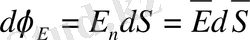
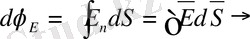 егер күш сызықтар тұйық ретте.
егер күш сызықтар тұйық ретте.
Электростатикалық өрістің суперпозиция принципі.
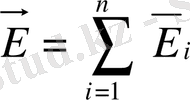
Өрістің қорытқы кернеулігі сол нүктедегі әрбір зарядтардың жеке-жеке тудырған өріс кернеулігінің геометриялық қосындысына тең.
Электрлік диполь деп - шамалары жағынан тең, система өрісі анықталатын нүктеге қарағанда ара қашықтығы е едәуір аз әр текші екі, +q және -q нүктелік зарядтан құрылған системаны айтамыз.
 диполь моменті
диполь моменті
Вакуумдағы электростатикалық өріс үшін Гаусс теоремасы
Радиусы
 сфералық бет арқылы өтетін Е векторының ағыны.
сфералық бет арқылы өтетін Е векторының ағыны.
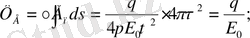
Бұл нәтиже әртүрлі пішінді тұйық бет үшін дұрыс болады.
N зарядты қоршап тұрған кез келген таңдап алынған жағдай үшін кернеулік векторының ағыны.
Суперпозиция принципі сәйкес өрістің кернеулігі барлық зарядтардың тудыратын кернеуліктерінің шамасына тең.
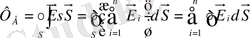
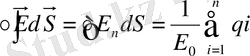 (1)
(1)
1 формула вакуумдағы өріс үшін Гаусс теоремасы деп атаймыз.
Бұл теорема бойынша вакуумдағы тұйық бет арқылы өтетін электростатикалық өрістің кернеулік векторының ағыны сол беттің ішіндегі зарядтардың алгебралық қосындысын Е 0 бөлгенге тең.
Егер заряд кеңістікте көлемдік тығыздық арқылы орналасса, онда Гаусс теоремасын мына түрде жазуға болады:
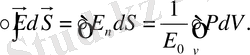
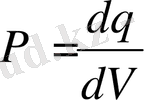
Гаусс теоремасын вакуумдағы өрістерге қолдану.
- Біркелкі зарядталған шексіз жазықтық өрісі.
Шексіз жазықтық тұрақты беттік тығыздық арқылы зарядталған.
+ Б
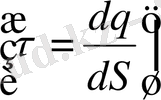 беттік тығыздық.
беттік тығыздық.
Тұйық бет ретінде ойша цилиндр тұрғызамыз оның табаны зарядталған жазықтыққа 11, ал осі оған
 болады.
болады.
Цилиндр арқылы өтетін барлық ағын оның табаны арқылы өтетін ағындардың қосындысына тең.
2ЕS Сонда Гаусс m-сы бойынша электрлік кернеудің өрісі.
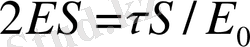
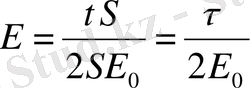 өріс кернеулігі
өріс кернеулігі
- Біртекті зарядтанған сфералық беттің өрісі.
Радиусы R сфералық бет беттік тығыздықпен
 біркелкі зарядталған. Зарядтар біркелкі орналасқандықтан олардың тудыратын өрісі
сфералық симметриялы
болады.
біркелкі зарядталған. Зарядтар біркелкі орналасқандықтан олардың тудыратын өрісі
сфералық симметриялы
болады.
Ойша центрі зарядталған сфера болатын радиусы
 тағы бір сфера тұрғызамыз. Егер
тағы бір сфера тұрғызамыз. Егер
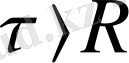 болса онда тұрғызылған бет ішінде барлық зарядтар болады. Гаусс теоремасы бойынша:
болса онда тұрғызылған бет ішінде барлық зарядтар болады. Гаусс теоремасы бойынша:
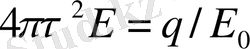
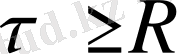 болса.
болса.
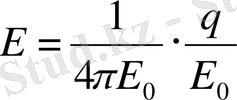
Бұл жағдайда нүктелік заряд сияқты өріс қашықтыққа байланысты азаяды.
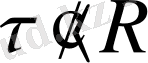 болса, онда тұйық беттің ішінде заряд болмайды. Сондықтан біркелкі зарядталған сфералық беттің ішінде өріс кернеулігі жоқ, ол 0-ге тең болады.
болса, онда тұйық беттің ішінде заряд болмайды. Сондықтан біркелкі зарядталған сфералық беттің ішінде өріс кернеулігі жоқ, ол 0-ге тең болады.
- Көлемдік зарядталған шар өрісі. Жалпы q зарядпен зарядталған шар (радиусы R ) көлемдік тығыздықпен зарядталған.
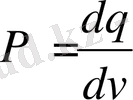
Сонда
Симметриялықты ескере отырып шардың сыртындағы кернеулік сфералық бет жағдайда мынадай болады:
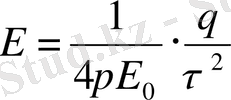
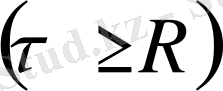

Бірақ шардың ішіндегі кернеулік басқаша, себебі:
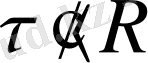 болса, онда
болса, онда
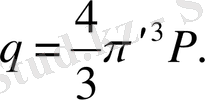
Ал өрісі Гаусс m-на байланысты
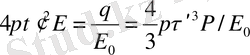
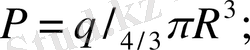
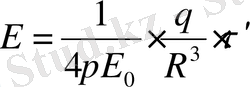
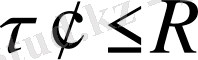
Біркелкі зарядталған шексіз цилиндр (жіп) өрісі.
Радиусы R шексіз цилиндр сызықтық тығыздықпен
зарядталған біркелкі
Гаусс Т-сы бойынша
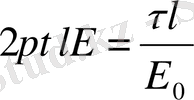
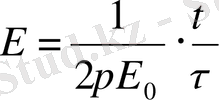
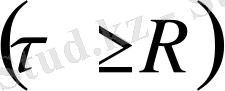
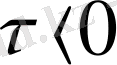

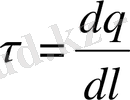
Өрістегі зарядтың орын ауыстыру жұмысы.
q 0 заряд q зарядының өрісінде орын ауыстырады, сонда оның жұмысы
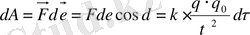
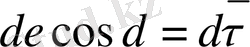
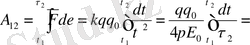
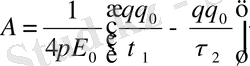 (1)
(1)
А 12 - орын ауыстыру орнына (траяк-на) ба йланысты емес тек бастапқы орны мен соңғы орнына байланысты, яғни нүктелік зарядтың электрлік өрісі потенциял өріс, ал электрлік күштер концервативті күштер деп атайды.
Егер заряд сыртқы электростатикалық өрісте тұйық контур бойынша орын ауыстырса онда оның жұмысы 0-ге тең болады.
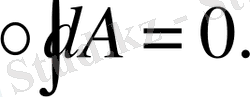 1
1
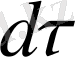
 2
2
q
 Equation. 3
Equation. 3
 Equation. 3
Equation. 3
 Equation. 3
Equation. 3
q +
Е векторының циркуляциясы.
Егер тасымалданатын заряд бірлік заряд болса онда de жолдағы күштің элементар жұмысы мынаған тең болады:
(2)
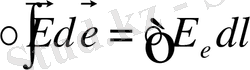
 циркуляциясы
циркуляциясы
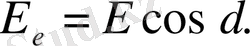
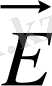 циркуляциясы туралы теорема.
циркуляциясы туралы теорема.
2 - формуланы мына түрде жазуға болады.
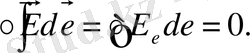 (3)
(3)
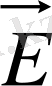 циркуляциялық туралы теорема.
циркуляциялық туралы теорема.
Осындай қасиетке ие күш өрісі потенциалдық өріс деп атайды.
Зарядтың потенциалдық энергиясы.
Консервативті күштің жұмысы потенциалдық энергияның азаю есебінен болады, яғни:
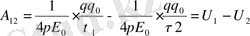
(4)
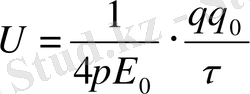 q зарядының өрісіндегі одан
q зарядының өрісіндегі одан
 қашықтығы
қашықтығы
q 0 зарядының потенциалдық энергиясы.
Егер өріс N нүктелік зарядтар жүйесінен пайда болса онда q 0 зарядтың потенциалдық энергиясы әр зарядтардың тудыратын энергияларының қосындысына тең.
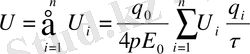
Потенциал
Электростатикалық өрісінің кез келген өрісіндегі потенциалы бірлік оң зарядтың сол нүтеге орналасқан потенциалдық энергиясымен анықталатын физикалық шама.
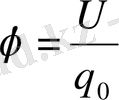
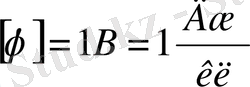
Нүктелік зарядтың потенциалы
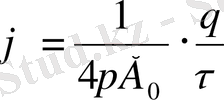
Өрістегі зарядтың орын ауыстыру жұмысы.
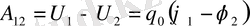 (1)
(1)
q 0 зарядты бір нүткеден екінші нүктеге ауыстырғандағы жұмыс мына формуламен анықталуы мүмкін:
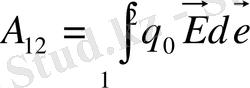 (2)
(2)
Потенциалдар айырымы
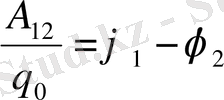
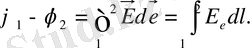
Егер q 0 зарядты өрістен алып шықсақ, яғни шексіздікке алып шықсақ онда шарт бойынша потенциал 0-ге тең болады.
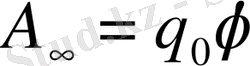
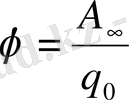
Потенциал дегеніміз - бірлік оң зарядты берілген нүктеден шексіздікке қарай алыстату жұмысымен анықталатын физикалық шама.
Электростатикалық өрістің суперпозиция принципі
Егер өріс бірнеше зарядтардан пайда болса онда зарядтар жүйесінің өріс потенциалы осы зарядтардың өріс потенциалдарының алгебралық қосындысына тең.
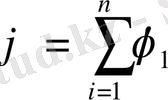
Кренеулік пен потенциал арасындағы байланыс.
Эквипотенциал беттер
Бірлік нүктелік зарядты бір нүктеден екінші нүктеге х өсі бойымен орын ауыстырғанда х
1
, х
2
нүктелер арасы өте жақын болғанда х
2
- х
1
= dx E
x
dx
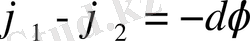
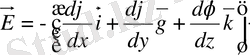
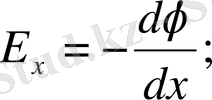
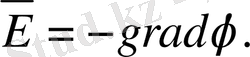
Эквипотенциал беттер дегеніміз - барлық нүктелерінде потенциалдың мәні бірдей болатын беттер.
Потенциалдың таралуын графикалық түрде көрсетуге болады.
Сонда
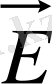 векторы эквипотенциал беттерге
векторы эквипотенциал беттерге
 болады және
болады және
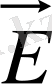 әрқашан потенциалдың азаюына қарай бағытталады.
әрқашан потенциалдың азаюына қарай бағытталады.
Потенциалдар айырымын яғни өріс кернеулігі бойынша есептеу
- Біртекті зарядталған шексіз жазықтық өрісі.
Сонда екі нүктенің арасындағы потенциалдың айырымы жазықтықтың х 1 және х 2 қашанда жатады.
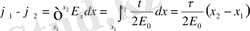
- Біртекті зарядталған сфералық беттің өрісі.
R - радиус
.
q - заряд
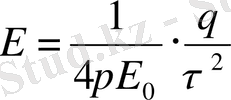
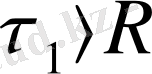
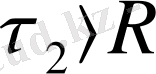
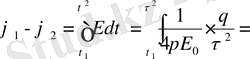
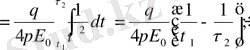 (1) фор.
(1) фор.
- Көлемдік зарядталған шардың өрісі.
R ; q.
(шар. сырт)
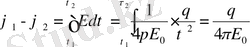
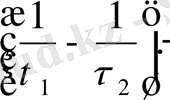
Шардың ішіндегі кез келген нүкте үшін
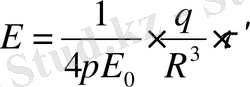
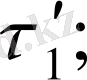
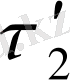 дейінгі арасындағы потенциал айырымы.
дейінгі арасындағы потенциал айырымы.
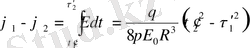
- Біртекті зарядталған шексіз цилиндр өрісі. (R) цилиндр сызықтың тығыздықпен зарядталған. (Цилиндр сыртында) яғнижәнеарасындағы потенциалдар айырымы.
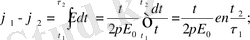
Диэлектрик түрлері.
Полярсыз молекулалы диэлектриктер.
N 2 , H 2 , O 2 , CO 2 .
Диэлектриктер дегеніміз - молекулалары симметриялы орналасқан, яғни оң және теріс зарядтардың ауырлық центрлері сыртқы электр өрісі жоқ кезде бір-бірімен сәйкес келетін және молекулалардың дипольдік моменті 0-ге тең болатын диэлектритер.
Полярлы молекулалы диэлектриктер.
H 2 O, NH 3 , SO 2 , CO.
Молекулалары сыртқы электр өрісі жоқ кезде дипольдік моментке ие болатын диэлектриктер.
Сыртқы өріс жоқ кезде полярлық молекулалардың дипольдік моменті жылдық қозғалыс әсерінен кеңістікте бейберекет орналасқан ал олардың қорытқы моменті 0-ге тең болады.
Ионды диэлектриктер.
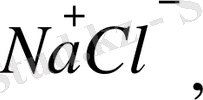
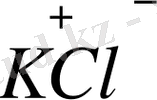
Иондық кристалдары кеңістіктегі торды беретін және әртүрлі таңбадағы иондар дұрыс немесе міндетті түрде қайталанып отыратын диэлектриктер.
Диэлектриктердің поляризациясы дегеніміз - дипольдардың бағытталуы немесе электр өрісі әсерінен дипольдардың пайда болуы.
- Электрондынемесе диформацияланған поляризация.
- Бағытталған яғни дипольді поляризация.
- Иондық поляризация.
Полярлану дегеніміз - бірлік көлемдегі диэлектриктің диполь моментімен анықталатын шама.
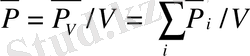

Н - диэлектрикті қабылдағыш.
Диэлектрикті сыртқы электр өрісіне енгізген кезде полярланады, оң жағында оң зарядтар болады. Оның беттік тығыздығы
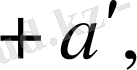 ал сол жағында теріс зарядтар болады, оның беттік тығыздығы
ал сол жағында теріс зарядтар болады, оның беттік тығыздығы
 бұл бір - бірімен нейтралданбаған зарядтар диэлектрик поляризация әсерінен болады, сонда байланысқан зарядтардың өріс кернеулігі
бұл бір - бірімен нейтралданбаған зарядтар диэлектрик поляризация әсерінен болады, сонда байланысқан зарядтардың өріс кернеулігі
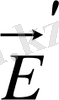 нейтралданған зарядтар өріс кернеулігі
нейтралданған зарядтар өріс кернеулігі
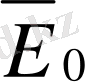 диэлектрик ішіндегі қорытқы кернеулігі мынаған тең:
диэлектрик ішіндегі қорытқы кернеулігі мынаған тең:

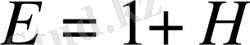
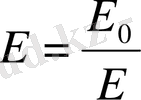
Ортаның диэлектрик өтімділігі дегеніміз ортаның өрісі диэлектрик қаншалықты әлсірейтінін көрсететін физикалық шама.
Электрлік ығысу
Электр өрісінің кернеулігі ортаның қасиеттеріне байланысты. Е векторы диэлектриктіктің шекарасынан өткен кезде секнске ұшырайды.
Сондықтан Электрлік ығысу деген шама енгіземіз.
Д - электрлік ығысу.
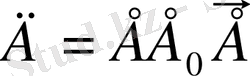 біртекті орта үшін.
біртекті орта үшін.

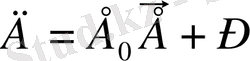
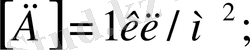
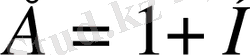
Қорытқы өріс диэлектриктері Е векторымен сипатталады. Ал Д векторы еркін зарядтарды тудыратын электростатикалық өрісті сипаттайды.
Диэлектрикте пайда болатын байланысқан зарядтар еркін зарядтардың бөлінуіне әсер етеді (тудырады) .
Бірақ, диэлектрик бар кезде еркін зарядтардың кеңістікте таралуы диэлектриктің бар болуына байланысты.
Электрлік ығысудың сызықтары дегеніміз кез келген нүктеде жанамалары Д векторының бағытымен сәйкес келетін сызықтар. Олардың бағыты және қоюлығы Е векторының сызықтары сияқты.
Байланысқан зарядтар бар жердегі Д векторының сызықтары үздіксіз болады.
Электр ығысуының вектор ағыны
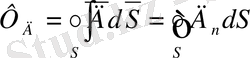
Диэлектриктегі электростатикалық өріс үшін Гаусс теоремасы
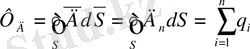
Екі диэлектриктік ортаның шекарасындағы шарттар
Е 1
Е 2 Д
Біртекті изотропты екі диэлектрик шекарасындағы Е және Д векторлары арасындағы байланысты қарастырамыз, бұл жағдайда шекарада еркін зарядтар жоқ. 1 және 2 диэлектриктің шекарасының айналасында АВСДА деген тікбұрышты контур тұрғызамыз.
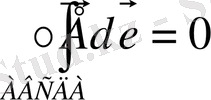


Екі диэлектриктің шекарасына биіктігі өте аз тік цилиндр тұрғызамыз. Оның бір табаны 1-ші диэлектрикте тұрады, екінші табаны 2-ші диэлектрикте тұрады.
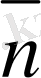 Д S
Д S
E 1 1
E 2 2
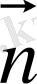
Сонда Гаусс теоремасы: Олардың әрқайсысында Д векторы бірдей болатындай аз.
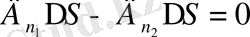

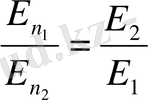
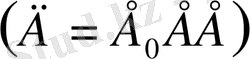
Осылайша екі диэлектриктің шекарасынан өткен кезде Е векторының
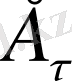 құраушысы Д
n
құраушысы үздіксіз өзгереді ал Е
n
құраушысы
құраушысы Д
n
құраушысы үздіксіз өзгереді ал Е
n
құраушысы
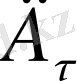 құраушысы секнске ұшырайды.
құраушысы секнске ұшырайды.
Өткізгіштердегі электр өрісі
Өткізгіштің ішіндегі өріс кернеулігі
Егер өткізгішті сыртқы электростатикалық өріске орналастырсақ немесе оны зарядтасақ онда өткізгіштің зарядтарына электростатикалық өріс әсер етеді де олар зарядтар тепе-теңдікке түскенше қозғалады. Ал тепе-теңдікке келген кезде өткізгіштегі электростатикалық өріс 0-ге тең болады.
Өткізгіштің ішіндегі кернеулік 0-ге тең.
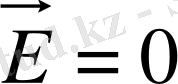
Зарядтар тек қана өткізгіштің бетінде ғана орналасады.
Өткізгіштің эквипотенциал беттер
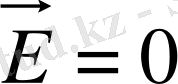 тең болғандықтан
тең болғандықтан
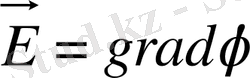 болса, өткізгіштің ішіндегі барлық нүктедегі потенциал бірдей.
болса, өткізгіштің ішіндегі барлық нүктедегі потенциал бірдей.
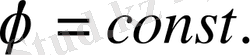 Сонда электрикалық өрістегі өткізгіштің беті эквипотенциал болады. Е векторы өткізгіштің бетіне тұрғызылған әр бір нүктеге тұрғызылған нормаль бойынша бағытталады.
Сонда электрикалық өрістегі өткізгіштің беті эквипотенциал болады. Е векторы өткізгіштің бетіне тұрғызылған әр бір нүктеге тұрғызылған нормаль бойынша бағытталады.
Өткізгішке жақын жердегі Е және
 арасындағы байланыс
арасындағы байланыс
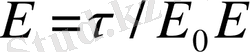
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz