Коммерциялық негізде жұмыс істейтін шаруашылық жүргізуші субъектілердің қаржысы
Қазақстан Республикасының Білім және Ғылым министрлігі
Әл-Фараби атындағы Қазақ ұлттық университеті
Экономика және бизнес факультеті
Қаржы кафедрасы
Курстық жұмыс
Тақырыбы: КОММЕРЦИЯЛЫҚ НЕГІЗДЕ ЖҰМЫС ІСТЕЙТІН ШАРУАШЫЛЫҚ ЖҮРГІЗУШІ СУБЪЕКТІЛЕРДІҢ ҚАРЖЫСЫ
Орындаған:ЕштайбековН. Ж.
Тобы: Ф08К4
Тексерген:Керімбекова Н. Н.
Алматы 2010
Жоспар:
- Кіріспе
- Теориялық негіздер
- Лабораториялық жұмыстың орындалуын сипаттау
Пайдаланылған әдебиеттер
Кіріспе
Лабораториялық жұмыстың мақсаты - эконометрика пәні бойынша алған теориялық білімдерді практика жүзінде көрсету.
Кредит беруші 10 компания көрсеткіштері негізінде көптік сызықтық регрессия теңдеуін құру.
Құрылған теңдеу үшін мыналарды есептеп табу қажет:
- корреляция коэффициенті
- детерминация коэффициенті
- регрессия коэффициенттерінің сенімділік интервалы
- Фишер статикасы
- икемділік коэффициенті
- апроксимацияның орташа қатесі
- гипотезаны тексеру.
Құрылған модельдің регрессия коэффициенттеріне интерпретация беру. Барлық есептеулерді Excel-де формулаларды және «Талдау пакетін» қолдана отырып жүзеге асыру. Формулалар және «Талдау пакеті» арқылы алынған нәтижелерді өзара салыстыру.
Теориялық негіздер
Регрессия терминін 19 ғасырдың соңында ата-аналары мен балаларының арасындағы бой өсуін бақылау барысында Фрэнсис Галтон енгізген болатын. Галтон өте ұзын ата-анадан сол екеуінің орташа бойынан ұзынырақ бала болады деп көрсетіп кетіпті. Ал балалардың бойы сол аумақта тұратын адамдардың орташа бойына теңеседі. Осыдан, осы тәуелділікті көрсететін термин пайда болса керек.
Қазіргі кезде регрессия термині түсіндірме шартты математикалық күтім мен соған тәуелді түсіндірілетін ауыспалы арасындағы байланысты көрсету ( Яғни Х өзгеруі У өзгерісіне қалай әсер етеді дегендей) дегенді білдіреді.
Көп жағдайларда біз регрессия моделін құрған кезде айнымалыларға әсер ететін көптеген факторларды елемеуіміз мүмкін. Сондықтан да кез келген модельде ауытқу пайда болады. Ал эмпирикалық мәліметтерге және зерттеу мақсаттарымен сай үйлесетін сапалы регрессия теңдеуін құру күрделі әрі сатылы құбылыс. Оны 3 кезеңге бөлуге болады. :1
- Регрессия теңдеуінің формуласын таңдап алу;
- Таңдап алынған теңдеудің параметрлерін анықтау;
- Теңдеудің анализінің сапасын анықтау және теңдеуді жетілдіру
Көптік сызықтық регрессия
Экономикалық көрсеткіштердің арасындағы өзара байланыстарды анықтау - экономикадағы негізгі проблемалардың бірі. Кез келген экономикалық политиканың негізі - ол экономикалық айнымалыларды реттеү, демек, бұл айнымалылардың басқа айнымалыларға қалай әсер етүін білүдің маңызы өте зор.
Анықтама: екі айнымалы арасындағы статистикалық байланыс формуласы жұптық регрессия , ал көп айнымалылар арасындағы формула көптік регрессия болады.
S(a, b) =∑Ei = ∑(yi - yxi) ² →min
Мұндағы yxi=a+bxi регрессия теңдеүі бойыеша есептелген мәндер; xi, yi - бақылау деректері; a, b - белгісіз параметрлер.
S(a, b) функциясы үздіксіз, дөнес және төменгі жағынан нөлмен шектелген, яғни минимумы бар функция түрінде көрсетілген әдісті ең кіші квадраттар әдісі деп атайды.
Кез келген экономикалық көрсеткішке бір ғана емес, көбінесе бірнеше факторлар әсер етеді. Мысалы кейбір тауарға сураныс тауар бағасымен ғана емес, басқа оны алмастыратын және толықтыратын тауарлармен, тутынушы табысымен және көптеген басқа факторлармен анықталады.
Бұл жағдайда екі айнымалының сызықтық регрессияның заңды жалғасы - көптік регрессия моделі қарастырылады:
yi=β 0 +β 1 x i1 +β 2 x i2 +…. +β j x ji +…β m x mi +£
y i - тәуелді айнымалы (предикатор) - і -ші бақылаудың қорытынды белгісінің мәні.
х jі - і-ші бақылауға сәйкес j-ші фактордың мәні.
£ I - i-ші бақылауға сәйкес қорытынды белгінің кездейсоқ құраушысы.
β 0 - бос мүше, ол х 1 =х2= . . . =хп=0 болғандағы у-тің формальді мәнін көрсетеді.
- Теңдеуі:;
ỹ = a + b 1 x 1 +b 2 x 2
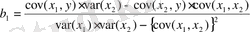
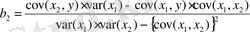
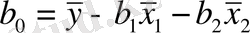
- Кіші квадраттар әдісі. Сызықтық регрессия теңдеуін бағалау үшін осы әдіс қолданылады.
3) Гаусс-Марковтың шарттары Кіші квадраттар әдісіне негізделген регрессиялық талдау ең жақсы нәтиже беру үшін Гаусс Марковтың келесідей төрт шарттары орындалуы керек. Себебі, регрессия коэффициенттерінің қасиеттері кездейсоқ құраушы коэффициентіне тікелей байлан ысты.
І. Е
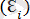=0. Кез келген байқау үшін кездейсоқ мүшенің математикалық күтімі Оге тең.
II. D
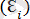=σ² . Дисперсия тұрақты.
III. cov(
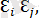) =0. Е(
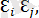) =0
IV. cov(
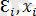) =0. E(
) =0. Кездейсоқ мүше түсіндіруші айнымалыдан тәуелсіз таралады.
Егерде төрт шарт орындалған жағдайда теңдеудің дұрыс шешім қабылдағанын көреміз. Гаусс Марков шарттары орындалса, а және в жұптық сызықтық регрессия коэффициентінің бағалары ығыспаған және тиімді болады. Яғни сызықтық ығыспаған бағалар ішінде ең кіші дисперсияға ие болады.
4) Гипотезанытексеру:
Регрессия коэффициенттеріне қатысты гипотезаны тексеру
Коэффициенттер мен оның бағасы b -ны қарастырайық. 2 гипотезаны ұсынуға болады:
- нольдік гипотезаН0: b=β0
- альтернативті гипотезаH1: b≠ β0
Егер Н 0 ақиқат болса b~N (β 0 ;
) орындалады. Яғни, қалыпты үлестіруінің ықтимал тығыздығының графигі
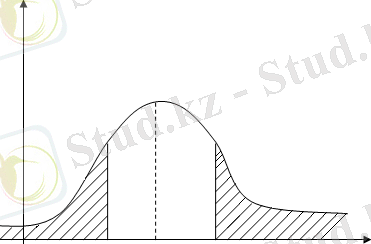
β 1 β 0 β 2
γ мәнділік деңгейін беріп, оның мәні β 1 -ң сол жағында, β 2 -ң оң жағында жату ықтималдығы γ болатындай β 0 - ге қатысты симметриялы [β 1 ; β 2 ] интервалды құрайды.
γ әдетте 1% және 5% мәндер деңгейіне сәйкес 0, 01 және 0, 05 деп алынады.
2 жағдай мүмкін болады:
1) Бағаланған b [β 1 ; β 2 ] интервалдан тыс жатуы мүмкін, оның ықтималдығы γ. Н 0 бағалау нәтижесіне қайшы, Н 0 қабылданбайды.
2)
b
[β
1
; β
2
]
жатса,
Н
0
қабылданады.
Бұл гипотезаны тексеру үшін Стьюденттің t -статистикасын қолданамыз:
Н 0 : b=β 0
t
b
=
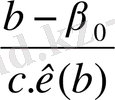
t b < t кр Н 0 қабылданады
t b > t кр Н 0 қабылданбайды
Коэффициенттердің мәндерін бағалау
;
;
;
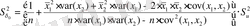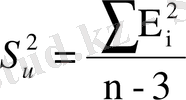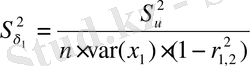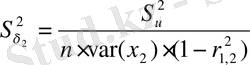
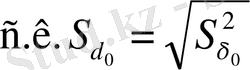
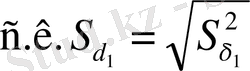
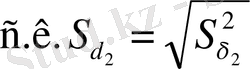
Коэффициенттер мәндерін тексеру:
1) H 0 : b i =0 i = 0, k
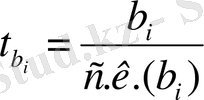
Жұптық регрессиядан айырмашылығы - еркіндік дәрежесі саны n-k-1-мен анықталады.
t bi < t кр болса, H 0 қабылданады, коэффициенттері сәйкес, мәнсіз
t bi > t кр болса, H 0 қабылданбайды, коэффициенттері сәйкес емес, мәнді
- Сенімділік интервалдары
b 0 : [b 0 -c. k(b 0 ) *tkr; b 0 +c. k(b 0 ) *tkr]
b 1 : [b 1 -c. k(b 1 ) *tkr; b 1 +c. k(b 1 ) *tkr]
b 2 : [b 2 -c. k(b 2 ) *tkr; b 2 +c. k(b 2 ) *tkr]
6) Детерминация коэффиценті
;
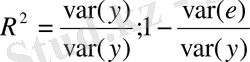Equation. 3
7) Фишер статистикасы
Жалпы сапасын тексеру үшін:
H 0 : R 2 =0
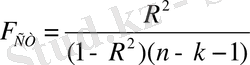
k 1 - тәуелсіз айнымалылар саны.
k 2 - еркіндік дәрежелік саны.
R 1 = k 1 - жалпы жағдайда
F кр = (k 1 , n-k-1)
Қорытынды:
F ст < F кр болса, H 0 қабылданады, R 2 - статистикалық мәнсіз, теңдеу сапасы нашар
F ст > F кр болса, H 0 қабылданбайды, R 2 - статистикалық мәнді, теңдеу сапасы жақсы.
8) Икемділік
деп у тәуелді және х факторлық белгілерінің ара-қтынасының өсу қарқынын көрсететін аналитикалық сипаттамасын айтады.
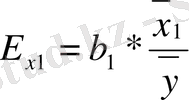
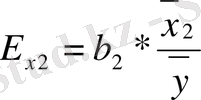
9) Апроксимация
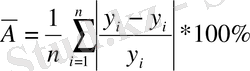
- 1-8 өте жақсы
- 8-10 жақсы
- 10-20 қанағаттандыралық
- 20 дан жоғары нашар.
Лабораториялық жұмыстың орындалуын сипаттау
Жай акциялар бағасы мен дивидендтері, компанияның табыстылығы туралы келесідей мәліметтер бар.
Көптік регрессияның сызықтық теңдеуін құру және оның параметрлерінің экономикалық мағынасын түсіндіру көзделеді.
Осы мәліметтер бойынша есептеулер кестесін құрамыз.
2-кесте
Нәтижелік көрсеткіштің оны анықтайтын факторлар арасындағы байланысты көптік регрессия теңдеуі арқылы көрстеуге болады. Сызықтық көптік регрессия теңдеуі мына жолмен анықталады:
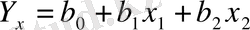
Теңдеу (
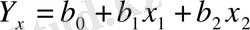) құру үшін алдымен b0, b1 және b2 параметрлерін анықтау қажет. Бұл көрсеткіштерді төмендегі теңдеулер арқылы есептеуге болады:
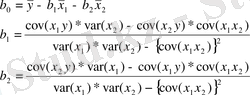
2-кестедегі есептелген мәліметтер бойынша көптік сызықтық регрессия теңдеуі мынадай түрде болады:
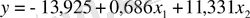
b 1 және b 2 коэффициенттерінің экономикалық мәні - байланыс күшінің көрсеткіштері, яғни қандай да бір факторлық белгінің өзгерісі нәтижесінде акция бағасының өзгерісін көрсетеді. Капитал табыстылығы бір пайыздық пунктке өзгерсе, акция бағасы сол бағытта 0, 686 АҚШ долларына өзгереді. Сонымен қатар, дивидендтер деңгейі бір пайыздық пунктке өзгерсе, акциялар бағасы сол бағытта 11, 311 АҚШ долларына өзгереді.
Ковариация - бұл екі кездейсоқ шамалар арасындағы сызықтық байланысының өлшемі болып табылады.
Егер ковариация оң мәнді болса, онда кездейсоқ шаманың біреуінің өсуі кезінде екінші кездейсоқ шаманың өсуі байқалады. Ал егер мәні теріс болса, яғни алдында «минус» таңбасы болса, онда керісінше кему тенденциясы байқалады.
Алайда, ковариацияның абсолютті мәні бойынша шамалар өзара қаншалықты байланысты екені туралы жорамалдауға болмайды, себебі ковариация масштабы олардың дисперсияларына тікелей байланысты.
Бұл масштабты ковариацияның мәнін стандартты ауытқу туындысына бөлу арқылы нормалауға болады. Бұның нәтижесінде біз әрқашан -1 және 1 сандар аралығында жататын Пирсонның корреляция коэффициентін аламыз.
Факторлық және нәтижелік көрсеткіштер арасындағы тығыздықты өлшеу үшін корреляция коэффициенті есетелінеді. Мынадай формула арқылы есептеуге болады:
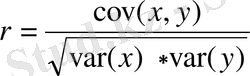
R xy мәні [-1, 0; + 1, 0] сандар аралығында жату керек. 1-ге санның мәні жақын болған сайын зерттелініп отырған құбылыстар арасындағы байланыстың тығыз болғандығын көрсетеді, және керісінше. Біздің мысалымызда R xy =-0, 029 тең болды.
Сызықтық регрессияны бағалау үшін кіші квадраттар әдісі қолданылады. Мақсаты - ауытқуды минималдау болып табылады.
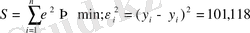
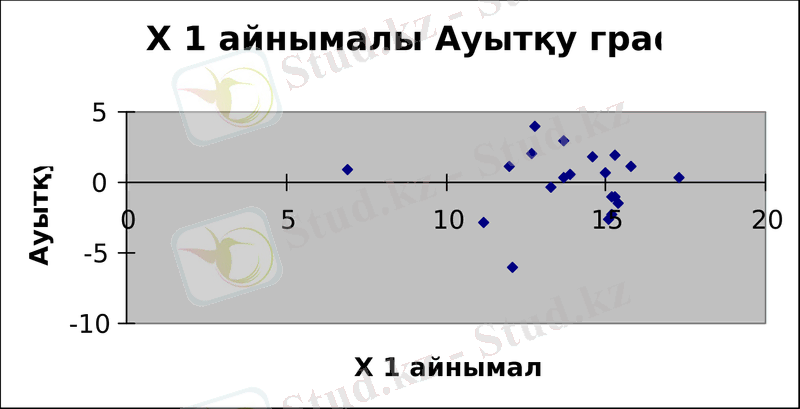
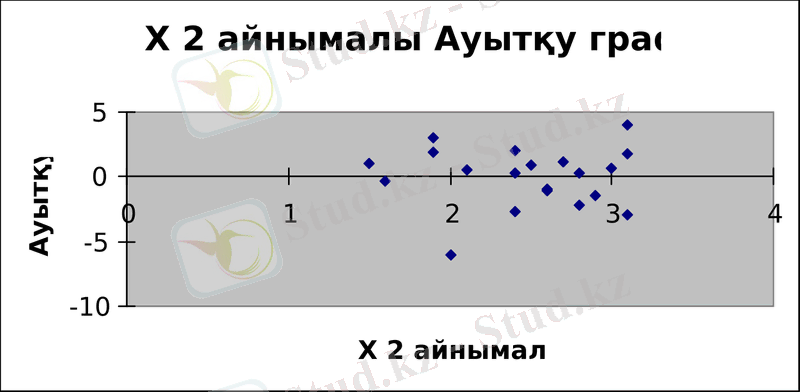
Гипотезаны тексеру үшін Стьюденттің t-статистикасын қолданамыз. Гипотезаны тексеру мақсаты - бұл таңдамалық бақылау мағлұматтары ұсынылған гипотезаға қарсы келетінін не келмейтінін анықтау болып табылады. Бұл тексеру арнайы құрылған критерийлер арқылы анықталады.
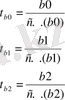
Бөліміндегі стандартты қате мынадай жолмен есептелінеді:
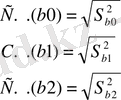
Мұндағы:
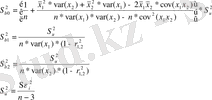
t-критикалық мән еркіндік дәреженің саны мен мәнділік деңгейіне байланысты болады. Мәнділік деңгейі әдетте 1%, 5% деп алынады. Еркіндік дәреженің саны жұптық регрессия үшін (n-3) -ке тең болады. t кр =n-3
Гипотезаны тексеру кезінде мынадай нәтижеге келдік:
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.
Ақпарат
Қосымша
Email: info@stud.kz