Леонтьев моделі мен салааралық баланстың математикалық негіздері


ӘЛ - ФАРАБИ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ УНИВЕРСИТЕТІ
Экономика және бизнес факультеті
Макро-микроэкономика кафедрасы
БАЯНДАМА
Тақырыбы: Леонтьев моделі
Орындаған:
Ғылыми жетекші:
АЛМАТЫ 2008ж.
Салааралық баланстың математикалық моделін американ экономисті В. Леонтьев жасап шығарған. Кейін ол әлемнің көптеген елдерінде, оның ішінде АҚШ пен КСРО-да кеңінен қолданған
Экономикалық өсім мен даму мәселелерін зерттеу мақсатында Леонтьев түпкілікті сұраныс тізіміне капиталға қажеттілік көрсеткіштерін қосу арқылы кезіндегі статикалық «шығындар-шығару» модель анализінің динамикалық нұсқасын әзірледі. Құрама штаттардың сауда министрлігі шахматтық баланстарды кейбір американ қалалары үшін әр бесжылдық ішінде жасап отырған. Біріккен Ұлттар Ұйымы, Әлемдік Банк және Советтер Кеңесінің Үкіметі экономикалық жоспарлау мен үкіметтің бюджеттік саясаты мен экономикалық жоспарлау саласында «шығындар-шығару» әдісі маңызды құрал ретінде қолданылды. «Шығындар-шығару» экономикалық моделін қолданудағы табысқа жетуінің басты себебі - халықаралық сауда, монополия теориясы, эконометрика сияқты ғылымдарды зерттеген кең салалы экономистің болуы.
Леонтьев 1973 ж. «Шығындар-шығару әдісін дамыту мен оның маңызды экономикалық мәселелерге қолдануына байланысты» экономика бойынша Нобель сыйлығының иегері болды. Экономикалық белсенділіктің қоршаған ортаға әсерін зерттеу мақсатында әлемдік экологияға қатысты қарапайым «шығындар-шығару» моделін құрған, онда қоршаған ортаны ластау дербес сектор ретінде көрсетілген
Экономикадағы салааралық баланс - бұл экономикалық жүйенің әртүрлі секторлары арасындағы байланыстарды анықтау анализінің әдісі.
Белгілі бір экономикалық жүйені белгілі тауарлар мен қызметтерді өндіруші бірнеше салаға бөлеміз деп тұжырымдайық. Бұл тауарлар мен қызметтерді өндіру кезінде әр сала басқа салалармен қатар, өзінің ресурстарын тұтынады. Яғни әр сала салааралық байланыстар экономикасында бір уақытта өндіруші және тұтынушы болады.
Баланстық анализдің мақсаты - экономикалық жүйенің оның өніміндегі барлық қажеттілігін қамтамасыз ету үшін әр сала қанша өнім өндіру керектігін білу.
Салаарлық байланыстардың ашық жүйесін қарастырамыз. Ондағы өндірілген барлық өнім (жалпы өнім) екі бөлікке бөлінеді: өнімнің бір бөлігі (аралық өнім) өндіруші салалардағы тұтынуға жұмсалады, ал басқа бөлігі (түпкілікті өнім) материалды өндіріс саласынан тыс түпкілікті сұраныс секторында тұтынылады. Сонымен қатар түпкілікті сұраныс секторындағы тұтыну өзгеруі мүмкін.
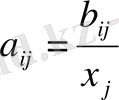 -
j
секторы өнімінің бір бірлігін өндіру кезінде шығындалатын
i
секторының өнім көлемі (
тікелей шығындар коэффициенттері
) ;
-
j
секторы өнімінің бір бірлігін өндіру кезінде шығындалатын
i
секторының өнім көлемі (
тікелей шығындар коэффициенттері
) ;
Салаарлық баланс - әр өндіруші сектор шығару көлемінің өндірістік секторлар мен түпкілікті сұраныс секторы тұтынатын өнімнің сомалық
көлеміне тең болуы керек
Соңғы теңдіктер өндіріс технологиясы мен экономикалық байланыстар құрылымын сипаттайды. Олар өндіруші секторлар қажеттіліктерін қамтамасыз етілгеннен кейін қалған өндірілген өнім бөлігі түпкілікті тұтыну секторына түседі. Егер шығару векторын Х, сұраныс векторын (түпкілікті өнім векторын) - У, ал элементтері тікелей шығындар коэффициенттері a ij болатын құрылымдық матрицаны А арқылы белгілейтін болсақ, баланс қатынасы матрицалық түрде келесідей болады:
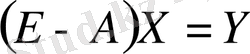
мұндағы Е- бірлік матрица .
Салааралық баланстың негізгі мақсаты - экономикалық жүйенің балансы жағдайындағы берілген құрылымдық А матрицасымен У берілген сұранысты қамтамасыз ету үшін Х жалпы шығарылым көлемін анықтау.
Егер матрица қайтарымды болса, онда бұл есептің шешімі келесідей болады:
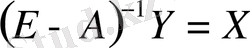 (24)
(24)
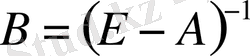 матрицасы толық шығындар матрицасы деп аталады.
матрицасы толық шығындар матрицасы деп аталады.
Көп салалы экономиканың статистикалық сызықтық моделін қарастырайық. Модельдің негізінде келесі тұжырымдар жатады:
- экономикалық жүйеде n өнімдер өндіріледі, сатылады, сатып алынады, тұтынылады және инвестицияланады;
- әрбір сала «таза» болып келеді, сондай-ақ тек бір өнім өндіреді, әртүрлі өнімдерді бірігіп өндіру болмайды. Әртүрлі сала әртүрлі өнімдер өндіріп шығарады;
- әр саланың өндірістік процесі ретінде кейбір (мүмкін барлық) өнім түрлерінің нақты бір өнімге айналуы болып табылады. Шығарылған және жұмсалған өнім қатынасы тұрақты деп болжамданды. Сонда, егер j-өнім бірлігін өндіру өндіру үшін i-ші өнімнің aij бірлігін жұмсау керек болса, онда j-өнімнің λ бірлігін шығару дегеніміз i-өнімнің λaij бірлігін қажет етеді деген сөз.
Xi жылда i-өнімнің жалпы шығарылымы 2 бөлікке бөлінеді: барлық салада өндірістік тұтынуға және соңғы тұтынуға (өндірістік емес) .
Алдыңғы айтылған үш тұжырымда барлық салаларда i-өнімді өндірістік тұтыну ∑aijxj тең, сондықтан i-өнімнің таза шығарылымы мынаған тең:
Xi-∑aijxj; j=1, …, n
Егер әрбір і-өнімнің таза шығарылымы мен оған деген соңғы сұранысты yi теңестірсек, онда
Xi-∑aijxj=yi, j=1, …, n
Бұл Леонтьев моделі.
Технологиялық матрица арқылы.

Әр сала үшін a ij (1) технологиялық коэффициенттерін қою арқылы келесі баланстық қатынасты аламыз:
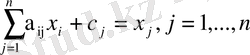
Бұл теңдеулер жүйесін векторлы түрде жазуға болады:
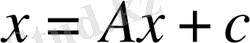 (1)
(1)
А- тұрақты технологиялық матрица;
с = (c 1 , . . . , c n ) - сұраныстың белгілі векторы;
x = (x 1 , . . . , x n ) - шығарудың белгісіз векторы
Бұл теңдеу Леонтьев моделі деп аталады.
Анықтама 1. Егер (1) жүйесінің x 1 ≥ 0, i = 1, . . . , n теріс емес шешімі болса, онда Леонтьев моделі өнімді деп аталады.
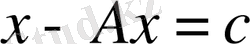
Сонда
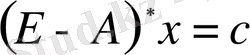 немесе
немесе
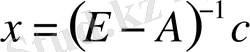
мұндағы Е- бірлік матрицасы.
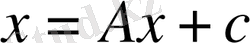 жүйесінің теріс емес шешімінің болуы (E - A)
-1
, яғни (E - A) матрицасына кері матрицаның бар болуымен түсіндіріледі. Сондай ақ, (E - A) теріс емес қайтарымды матрица болуы қажет, яғни (E - A) матрицасы анықталмаған (│A│≠ 0) (E - A)
-1
кері матрицасы теріс болмауы керек.
жүйесінің теріс емес шешімінің болуы (E - A)
-1
, яғни (E - A) матрицасына кері матрицаның бар болуымен түсіндіріледі. Сондай ақ, (E - A) теріс емес қайтарымды матрица болуы қажет, яғни (E - A) матрицасы анықталмаған (│A│≠ 0) (E - A)
-1
кері матрицасы теріс болмауы керек.
Леонтьев моделінің маңызды салдары болып оған екі нақты модельді қолдану арқылы алынатын нәтижелер табылады
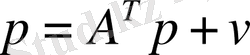 Equation. 3
(2)
Equation. 3
(2)
мұндағы A T - А транспонирленген матрицасы;
Бұл теңдеуді құндық мағына жағынан қарастыратын болсақ.
p = (p 1 , …, p n ) - салалардың өнімдерінің бағаларының векторы;
ν = (ν 1 , …, ν n ) - өнімнің бірлігіне қосылған құнның векторы (яғни тауарды өндіргеннен кейін оның құнына қосылуы) ;
A T p - өндіріс бірлігіне шығындар сомасының векторы ретінде көрсетуге болады;
p - A T p айырмасы өндіріс бірлігіне келетін шығындар векторы болып табылады. Осы таза табыс ν қосылған құнға теңестіріледі.
(2) теңдеуінің теріс емес p = (p 1 , …, p n ) шешімі бар болса, онда Леонтьевтің екі жақты моделі өнімді деп аталады. Бұл (1) және (2) екі жақты теңдеулерінің арасында тығыз математикалық байланыстың бар болуымен түсіндіріледі.
Теорема 1. Леонтьев моделі (1) өнімді болу үшін оған екі жақты (2) моделінің өнімді болуы қажетті және жеткілікті.
Леонтьев моделі әртүрлі экономикалық мақсаттарды анықтау үшін және түрлі ортақтылауларды жүзеге асыру үшін бастапқы нүкте болып табылады. Дәлелдеуі ретінде (1) теңдеуінің халықаралық сауда моделі ретінде және Леонтьев моделінің модификациясын оптимизациялау мақсаты ретінде көрсетеміз.
(1) теңдеуін сауда моделі ретінде көрсеткен кезде, n - өзара сауда жүргізетін елдер саны, x i - i елінің ұлттық табысы, c i - i елінің ұлттық шығындары, a ij - j елінің ұлттық табысының бірлігіне келетін i елінен j еліне импорттың көлемі. a ij элементіне i елінің өз өнімін ішкі тұтынуының коэффициенті мағынасы беріледі.
Бұл жағдайда Леонтьев моделінің барлық элементтері теріс емес болуы керек, өйткені ұлттық табыс пен ұлттық шығындар әрқашан оң шамалар болып табылады. Бұл жағдайда (1) моделі келесі сұраққа жауап береді: ұлттық шығындар мен елдер арасындағы тауарлар айырбасының тұрақты деңгейін қамтамасыз ететін елдің ұлттық табысының деңгейі қандай болуы керек?
Xi-∑aijxj=yi, j=1, …, n Бұл жүйенің екіжақтылығы деп өнімнің pj бағасы үшін сызықтық теңдеудің жүйесін айтамыз.
pj-∑aijpi=νj, i=1, …, n (3)
мұндағы, νj≥0 - j- сала шығарылымының бірлігіне қосылған құн.
∑aijpi - j- саланың шығарылымының бір бірлігіне кеткен шығын сомасы, (3) теңдеуінің сол жақ бөлігінде j- сала бірлік шығындарынан түскен таза табыс, ол қосылған құнға νj - ға тең.
Теорема 2. (3) жүйе табысты деп аталады, егер ол теріс емес pj≥0, j=1, …, n үшін орынды болса. Өнімділік пен табыстылық эквивалент, (1) өнімділіктен (3) табыстылық шығады, немесе керісінше.
«Шығындар - шығару» салааралық моделі
«Шығындар - шығару» салааралық моделінің шахматты таблицасы - өнім өндірудегі шығындар көлемінің арасындағы байланыстарды көрсетеді, әсіресе өндіруші салалардағы өнім көлемімен байланысты. «Шығындар - шығару» салааралық моделінің экономикалық математикалық негізін A(a ij ) тікелей материалдық шығындар коэффициенттері бар технологиялық матрица құрайды:
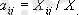 ,
i, j
= 1, 2, …,
n.
,
i, j
= 1, 2, …,
n.
(3) және (1) формула мынадай түрге келтіріледі:
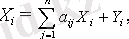
Немесе матрицалық түрде:
X = AX + Y.
Осы формулаға сәйкес келесі есептемелерді жүргіземіз:
1. Жалпы өнім арқылы ( X i ) әр сала үшін соңғы өнім көлемін анықтауға болады ( Y i ) :
2 i - саланың соңғы өнім шамасын бере отырып ( Y i ), әр саланың жалпы өнімінің шамасын анықтауға болады ( X i ) :
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz