Математикалық функциялар

Жоспар
Кіріспе

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
1 бөлім.Теориялық бөлім.
1.1.Функция ұғымы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
1.2.Функцияның берілу тәсілдері ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
2.1.Функцияның графиктік әдіспен берілуі ... ... ... ... ... ... ... ... ... ... ..
1.3.Элементар функциялар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
1.4.Шектелген функциялар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
1.5.Функцияның анықталу облыстарын табу жолдары ... ... ... ... ... ... ... ..
1.6.Монотонды функциялар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
1.7.Периодты функциялар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
1.8.Тақ және жұп функциялар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
2 бөлім.Функция тақырыбының оқыту әдістемесі.
2.1.Функцияның формуламен берілуі ... ... ... ... ... ... ... ... ... ... ... ... ... .
2.2.Функцияның кестемен берілуі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
2.3.Квадраттық функция және оның графигі ... ... ... ... ... ... ... ... ... ... .
3 бөлім.Практикалық бөлім.
Қорытынды
Қолданылған әдебиеттер

Функция (cәйкестік) анықтамасы: X және Y жиындары берiлсiн. Егер X және Y жиындарының арасындағы f сәйкестiгi бойынша X жиынының әрбiр элементiне Y жиынының бiр ғана элементi сәйкес қойылса, f сәйкестiгiн X жиынынанY жиынына бейнелеу деп аталады. Белгiлеуi: f: X→Y. Егер y элементi f бейнелеуi бойынша x элементiнiң бейнесi болса, оны f(x) = y теңдiгi арқылы жазамыз. Мұндағы x элементi y элементiнiң f бейнелеуі бойынша алғашқы бейнесi, ал y элементi x элементiнiң бейнесi деп аталады.
Егер X мүмкін мәндер жиынтығынан алынған х-тің әрбір мәніне айнымалы Y жиынының белгілі бір мәні у сәйкес келсе, онда у айнымалы шамасы х айнымалы шамасының функциясы деп аталады. Мұндай тәуелділік у=f(х) түрінде жазылады. f әрпінің орнына басқа әріптер де (мыс., F, т.б.) қолданылады. Мұндағы х-ті тәуелсіз айнымалы (кейде аргумент) деп, ал оның өзгеру облысы (жиыны) у-тің анықталу облысы деп аталады. х-тің өзгеруіне байланысты айнымалы у-тің қабылдайтын мәндерінің жиынын у функциясының өзгеру облысы деп атайды. Функцияның жоғарыда берілген анықтамасында назар аударатын екі жағдай бар: біріншісі — аргумент х-тің өзгеру облысын көрсету, екіншісі — х пен у мәндерінің арасындағы сәйкестік ережені немесе заңды тағайындау. Егер х-тің бір мәніне у-тің бір ғана мәні сәйкес келсе, онда у-ті х-тің бір мәнді Функциясы деп, ал егер х-тің бір мәніне у-тің бірнеше мәні сәйкес келсе, онда у-ті х-тің көп мәнді Функциясы деп атайды.
Айнымалы шамалар (х пен у) мәндерінің арасындағы сәйкестік ережені немесе заңды функц. тәуелділік дейді. Функция көбінесе аналитикалық тәсіл немесе формула арқылы (мысалы, , т.б.), кейде графиктік және таблицалық (дәл не жуық формулалармен есептелген) тәсілдерімен де беріледі. Математиканың одан әрі дамуы нәтижесінде Функция табиғаты кез келген айнымалы математикалық объектілер арасындағы сәйкестік ретінде жалпыланды. Математиканың басқа ұғымдары тәрізді Функция ұғымы да бірден қалыптасқан жоқ. Ол дамудың ұзақ жолынан өтті. “Функция” термині алғаш рет 1692 ж.Г.Лейбництің еңбектерінде кездесті. Функцияның қазіргі ұғымға жақын алғашқы анықтамасын И.Бернулли (1718) берген, ал бұл ұғымды Д.Бернулли, Л.Эйлер, Ж.Фурье, П.Дирихле, Н.И. Лобачевский, т.б. одан әрі дамытты.

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 26 бет
Таңдаулыға:

Мазмұны
Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
1 бөлім.Теориялық бөлім.
1.1.Функция ұғымы ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ...
1.2.Функцияның берілу тәсілдері ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... .
2.1.Функцияның графиктік әдіспен берілуі ... ... ... ... ... ... ... ... ... ... ..
1.3.Элементар функциялар ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... .
1.4.Шектелген функциялар ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... .
1.5.Функцияның анықталу облыстарын табу жолдары ... ... ... ... ... ... ... ..
1.6.Монотонды функциялар ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ...
1.7.Периодты функциялар ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ..
1.8.Тақ және жұп функциялар ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ...
2 бөлім.Функция тақырыбының оқыту әдістемесі.
2.1.Функцияның формуламен берілуі ... ... ... ... ... ... ... ... ... ... ... ... ... .
2.2.Функцияның кестемен берілуі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
2.3.Квадраттық функция және оның графигі ... ... ... ... ... ... ... ... ... ... .
3 бөлім.Практикалық бөлім.
Қорытынды
Қолданылған әдебиеттер

Кіріспе
Функция (cәйкестік) анықтамасы: X және Y жиындары берiлсiн. Егер X және Y жиындарының арасындағы f сәйкестiгi бойынша X жиынының әрбiр элементiне Y жиынының бiр ғана элементi сәйкес қойылса, f сәйкестiгiн X жиынынанY жиынына бейнелеу деп аталады. Белгiлеуi: f: X--Y. Егер y элементi f бейнелеуi бойынша x элементiнiң бейнесi болса, оны f(x) = y теңдiгi арқылы жазамыз. Мұндағы x элементi y элементiнiң f бейнелеуі бойынша алғашқы бейнесi, ал y элементi x элементiнiң бейнесi деп аталады.
Егер X мүмкін мәндер жиынтығынан алынған х-тің әрбір мәніне айнымалы Y жиынының белгілі бір мәні у сәйкес келсе, онда у айнымалы шамасы х айнымалы шамасының функциясы деп аталады. Мұндай тәуелділік у=f(х) түрінде жазылады. f әрпінің орнына басқа әріптер де (мыс., F, т.б.) қолданылады. Мұндағы х-ті тәуелсіз айнымалы (кейде аргумент) деп, ал оның өзгеру облысы (жиыны) у-тің анықталу облысы деп аталады. х-тің өзгеруіне байланысты айнымалы у-тің қабылдайтын мәндерінің жиынын у функциясының өзгеру облысы деп атайды. Функцияның жоғарыда берілген анықтамасында назар аударатын екі жағдай бар: біріншісі -- аргумент х-тің өзгеру облысын көрсету, екіншісі -- х пен у мәндерінің арасындағы сәйкестік ережені немесе заңды тағайындау. Егер х-тің бір мәніне у-тің бір ғана мәні сәйкес келсе, онда у-ті х-тің бір мәнді Функциясы деп, ал егер х-тің бір мәніне у-тің бірнеше мәні сәйкес келсе, онда у-ті х-тің көп мәнді Функциясы деп атайды.
Айнымалы шамалар (х пен у) мәндерінің арасындағы сәйкестік ережені немесе заңды функц. тәуелділік дейді. Функция көбінесе аналитикалық тәсіл немесе формула арқылы (мысалы, , т.б.), кейде графиктік және таблицалық (дәл не жуық формулалармен есептелген) тәсілдерімен де беріледі. Математиканың одан әрі дамуы нәтижесінде Функция табиғаты кез келген айнымалы математикалық объектілер арасындағы сәйкестік ретінде жалпыланды. Математиканың басқа ұғымдары тәрізді Функция ұғымы да бірден қалыптасқан жоқ. Ол дамудың ұзақ жолынан өтті. "Функция" термині алғаш рет 1692 ж.Г.Лейбництің еңбектерінде кездесті. Функцияның қазіргі ұғымға жақын алғашқы анықтамасын И.Бернулли (1718) берген, ал бұл ұғымды Д.Бернулли, Л.Эйлер, Ж.Фурье, П.Дирихле, Н.И. Лобачевский, т.б. одан әрі дамытты.

1 бөлім.Теориялық бөлім.
1.1.Функция ұғымы.
Тәуелсіз айнымалы х-тың әрбір мәніне тәуелді айнымалы у-тың бір ғана мәні белгілі бір ереже немесе заң арқылы сәйкестендірілсе,онда сәйкестік заңын функция деп аталады.
Тәуелсіз айнымалыны қысқаша аргумент, ал тәуелды айнымалыны функция деп аталады.Аргумент өзгеру кезінде кез келген мәнді қабылдайды,мысалы,х1.Бұған сәйкес функцияның мәні у1 немесе fх түрінде жазылады . fх1 - арументтің х1 мәніне f заңын қолданылатындығын,ал у1 сол заңды қолданғаннан кейінгі нәтижені көрсетеді.Мысалы,х1=3, ал f-квадыраттау десек,онда f = х12=32 деген мағына білдіреді,мұны у1=9 деп түсіну керек.
Аргумент х еркін өзгеретін болғандықтан, нақты сандардың кез келгенін қабылдай алады, ал f заңы бойынша оның кез келгеніне сәйкестендірілетін мән сан табылмауы мүмкін.Мәселен,у= √х функциясының аргументі х өзіне мән ретінде R=] -infinity,infinity [ нақты сандар жиынының кез келгенін қабылдай алады,ал квадрат түбірді тек оң саннан ғана табуға болады.х-тің оң сандар жиынындағы кез келген мәніне түбір табу ережесі бойынша бір оң у немесе х санын сәйкестендіруге болады.Осы Ех= [ 0,infinity [ аралығын √х функцияның анықталу обылысы дейді.
Функцияның мүмкіншілігіне байланысты аргументтің қабылдайтын мәндерінің жиыны Ех - функцияның анықталу обылысы, ал Ехжиыныа сәйкес тәуелді айнымалының жиыны Мf - функцияның мәндерінің обылысы деп аталады.
Осы жиындарды пайдаланып, фунцияның анықтамасын былай да тұжырымдауға болады.
Егер Ех жиынының әрбір х элементіне белгілі бір ереже немесе заң бойынша Мf жиынының тек қана бір элементі сәйкес қойылса, онда осы ережені функция деп аталады.Мәселен,у=х+1 теңдігі функция болады,өйткені х-тің әрбір мәніне сәйкес у-ті х-ке бірді қосып анықтауға болады.
Бір жиынның Ех - тің екінші жиынға Еf-ке ауысуы процесін бейнелеу, ал бейнелейтін функцияны оператор дейді және х∈Ех--f у∈Еf деп жазады.
Мысалы,у=√х функциясы өзінің анықталу обылысы Ех=[0,infinity[ жиынын оның мәндерінің жиынына бейнелейді және бұл процесті стелкамен х--√ у көрсетуге болады.

1.2.ФУНКЦИЯНЫҢ БЕРІЛУ ТӘСІЛДЕРІ
Функцияның берілу тәсілдері көп.Солардың ішінде математикалық анализ курсында функцияның графиктік, аналитикалық,сөзбен және кесте түрінде берілуі жиі кездеседі.
2.1. Функцияның графиктік әдіспен берілуі.
{(х,у); х∈Е, у=f(х)∈ М} қос сандар жиынын f х функциясының графигі деп аталады.Функцияның графигін координаттық жазықтыққа сызады.Өзара перпендикуляр екі координаттық түзу және оларға ортақ координаттар басы орналасқан жазықтықты координаттар жазықтығы дейді. Горизонталь орналасқан түзуді абсциссалар осі деп атайды да,х-пен белгілейді,вертикаль орналасқан түзуді ординаталар осі деп атап,у арқылы белгілейді, ал олардың қиылысу нүктесін координаттар басы дейді,оны 0 әріпімен белгілейді.Тәуелсіз айнымалы х-тің мәндері абсциссалар осіне салынады.Оң санға сәйкес нүктелер координаттар бас нүктесінің оң жағына,ал теріс санға сәйкес нүктелер оң сол жағына салынады.Ал у-тің мәндері оң болса,ординаталар осінің бойына координаттар бас нүктесінен жоғары қарай,ал теріс болса,төмен қарай салынады.Жазықтықтың әр нүктесіне оның координаттарын сәйкестеп қойсақ,біз жазықтық нүктелері мен қос сандар арасындағы сәйкестікті шығарып аламыз.Осы қос сандарға сәйкес нүктелер жиыны функцияның графигі болады.
Функцияның графигі 1.1-суретте көрсетілгендей тұтас сызық болуы да немесе 1.2-суреттегідей ажыратылған нүктелер түрінде де болуы мүмкін.

Y Y

0 X 0 X
1.1 сурет 1.2 сурет

2.Функцияның сөзбен берілуі.
Айнымалы екі шаманың арсындағы сәйкестік заңы сөзбен тұжырымдаса, онда функция сөзбен берілді делінеді.Математика сөзбен берілу тәсіліне мысал - Дирихле функциясы :
у=Д(х)= 1,егер х рационал сан болса ;0, егер х иррациоал сан болса ;

3.Функцияның кестелік тәсілмен берілуі.
Зерттелетін заңдылықты әр уақытта математикалық амалдар арқылы өрнектеу мүмкін бола бермейді. Кейбір жағдайларда бір айнымалының қай мәні екіншісінің қандай мәніне сәйкес келетін арнайы аспаптар арқылы ғана анықтауға болады,ал нәтижесі төмендегідей кестеге орналастырылады мысалы,уақытқа байланысты температураның өзгерісі .
Х
х1
х2
...
хк-1
хк
...
хn
...
У
у1
у2
...
ук-1
ук
...
уn
...

Функцияны бұл түрде берілуін функция кестелік әдіспен беріледі дейді.Кестелік әдіс көбінесе техникалық зерттеулерде қолданылады.Бұл әдістің ерекшелігі - қосымша өлшеулер және есептеулер жүргізбей-ақ, функцияның қажет мәнін кестеден бірден тауып пайдалануға болады.
4.Функцияның аналитикалық тәсілмен берілуі.
Айнымалылар арсындағы сәйкестік формуламен берілсе, онда функция анлитикалық түрде берілді дейді.
1 y=60x; 2 y=Пr2; 3 y=1-x2 4 y=sin x
Теңдіктері функцияның аналитикалық түрде берілуіне мысал бола алады.Аналитикалық түрде берілуде математикадағы амалдардың кез келгені пайдалануы мүмкін.Математикалық анализ курсын оқып үйренген сайын амалдар қатары көбейе түседі.

ЭЛЕМЕНТАР ФУНКЦИЯЛАР
1.Тұрақты функция

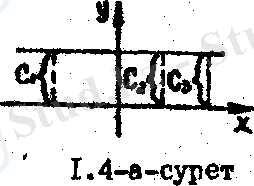
Тұрақты сан мен тұрақты функция ұғымдары әр түрлі ұғымдар.Мысалға у=С тұрақты функцияның геометриялық бейнесі абсциссалар осінен С қашықтықта жатқан және оған паралель түзу. Тұрақты функцияны қысқаша былай тұжырымдауға болады: нақты сандар облысында х-тің кез келген мәніне тек бір ғана С саны C1=C2=C3=C сәйкес қойылады 1.4а-сурет.Тұрақты санның геометриялық бейнесі - нүкте.

(

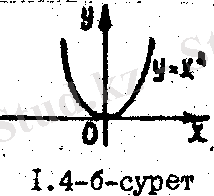
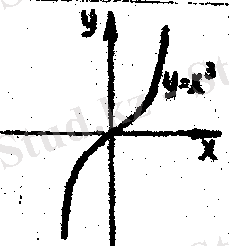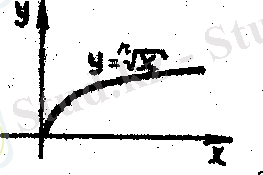
2.Дәрежелік функция
у=х түріндегі функция дәрежелік функция деп аталады, α - кез келген нақты сан, яғни α=n болғанда, y = f ( x ) = xn рационал фуекциясы шығады және ол сан түзуінде анықталады. n= 2.3 болғанда, y=x2 және y=x3 функциялары шығады. Бұлардың графиктерін тиісінше квадрат және куб парабола дейді 1.4-б.в-сурет .Осыған орай кейде xn функцияның графигін n-ші дәрежелі парабола деп те атайды.
Егер n бүтін теріс сан болса, яғни n = - mонда y=x-m = 1xm функциясын
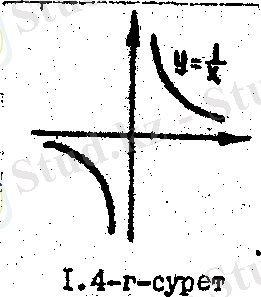
аламыз.Бұл функция координаттар жүйесінің бас нүктесінде анықталмайды,яғни ] - infinity; 0 [ u ] 0 ; infinity [ аралығында анықталады.m = 1 болғанда функциясы шығады және оның графигі тең бүйірлі гипербола болады 1.4-г- сурет.
Егер α=1n мұндағы n - оң бүтін сан болса,онда f ( x )=x1n=nx
иррационал функция шығады 1.4- е- сурет.
Қарастырылған мысалдарға сүйеніп, кез келген α үшін дәрежелік функцияны ] 0,infinity [ аралығында анықталыды деп айтуымызға болады.

2. Көпмүшелер
y= P n (x) = α0 x n- α1 xn-1 +...+ α n-1 x + α n функциясын қарастырайық, мұндағы n - бүтін сандар. Көпмүше дәрежелік функциялар мен тұрақты сандардың көбейтінділерінің қосындысы болғандықтан, ол бүкіл нақты сандар жиынында анықталады.
n=1 y=P1(x)=α0x + α1= α x+ b бірінші дәрежелі көпмүше аламыз,мұны сызықтық функция деп аталады. Ол нақты сандар жиынында, яғни ] - infinity; infinity [ аралығында, n=2 болғанда ]- infinity; infinity[ нақты сандар жиынында анықталған, графигі парабола болатын
y=P2(x) = α0x2 + α1x + α2 = α x2+ b x + c квадрат үшмүше аламыз, а 0 болса, параболаның тармағы жоғары,ал а 0 болғанда төмен бағытталады.

3.Бөлшек-рационал функция.
P n ( x ) = α0 xn + α1 xn-1 +...+ αn-1 x+ αn ,
Q m ( x ) = b0 xm+ b1 xm-1 +...+ bm-1 x + bm
Екі көпмүшенің қатынасы
У= R (x) = a0xn+a1xn-1+...+an-1x+anb0xm+b1xm-1 +...+bm-1x+bm=Pn(x)Qm(x)
Бөлшек-рационал функция деп аталады.Ол бөлімдегі көпмүше нөлге айналмайтын х-тің мәндерінің жиынында анықталған.
y=x-1x2+1 , y= x2+1x-1 , y=αx+bcx+d

Функциялары бөлшек-рационал функциялар.Соңғысы бөлшек-сызықты функция деп аталады.Егер анықтауыш
∆ = αbcd 0
Болса,онда бөлшек-сызықты функцияның графигі тең бүйірлі гипербаланың негізгі бөлігі және түзулерімен бөлінген координаттар жазықтығының бірінші және үшінші ширектерінде орналасады.Егер ∆ 0 болса, онда тең бүйірлі гипербаланың негізгі бөлігі екінші және төртінші ширектерде орналасады.Бөлшек-сызықты функция
] - infinity ; - dc [ U ] - dc ; infinity [
аралығында анықталады.

4.Көрсеткіштік функция
y= f(x)=ax түріндегі функция көрсеткіштік функция деп аталады. Ол х-тің кез келген мәнінде анықталады.Олай болса,корсеткіштік функция бүкіл сандар осінде яғни нақты сандар жиынында( ] - infinity; infinity [ аралығында) анықталған және а 0 болғанда функция мәндерінің жиыны оң сандар болады.
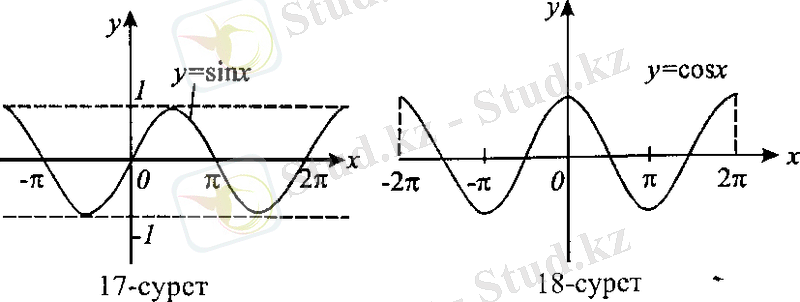
5.Тригонометриялық функциялар
y= sin x , y = cos x ,y= tg x , y= ctg x функциялары тригонометриялық функциялары деп аталады.Синус пен косинус функциялары бүкіл нақты сандар жиынында анықталған ал мәндері -1мен 1 арасында өзгереді:
y = sin x , Ex = ( - infinity, infinity ) , Ef=[ -1,1] ;
y = cos x , Ex=( - infinity, infinity ) , Ef=[ -1,1] .
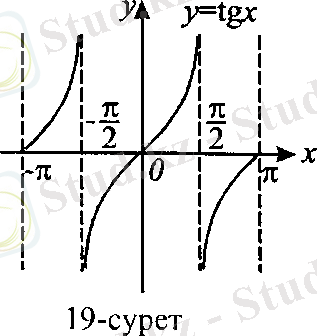
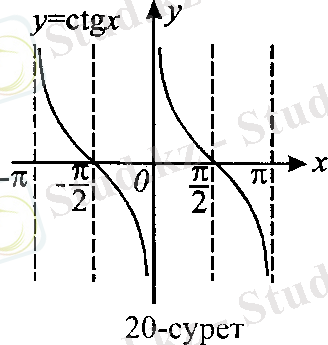
Тангенспен котангенс функцияларының анықталу обылысын табу үшін бүкіл сандар жиынынан тиісінше cos x = 0 және sin x = 0 теңдеулерінің шешімін шығарып тастау керек:
y=tg x = sinx cosx , Ex= {xx !=(2k-1)П2 ,k ∈ Z };
y=ctg= cosx sinx , Ex= {xx != kП , k ∈ Z }.

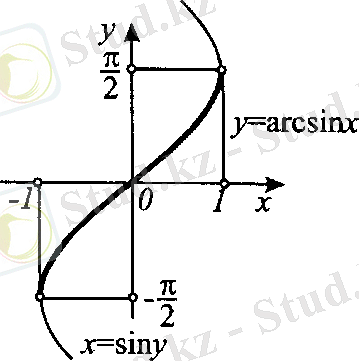
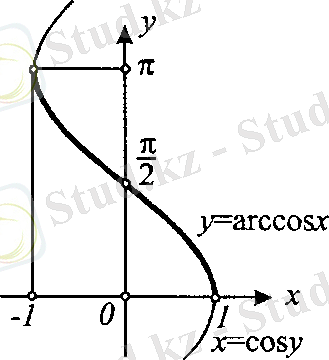
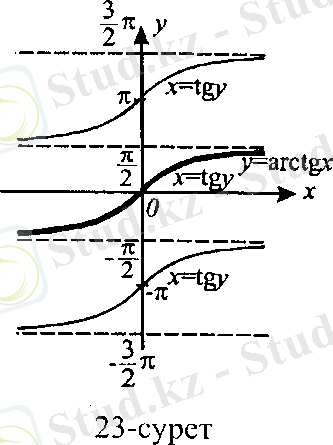
6.Кері функция
Айталық, y = f x функциясы А жиынын В жиынында бейнелейтін болсын.
В жиынының кез келген элементі у түшін f ( x ) = y теңдігі орындалатындай а жиынынан жалғыз ғана элемент табылса, онда В жиынында f функциясына кері φ = f -1 функциясы бар болды деп айтады да, x = φ ( y ) немесе x = f -1(y) деп жазылады, ал f-ті тура функция деп те аталады.
F функциясының мәндерінің жиыны φ кері функциясы немесе f -1-дің анықталу обылысы болады,ал тура функцияның анықталу обылысы кері функцияның мәндерінің жиыны болады. F - ке кері φ функциясы бар болу үшін оның анықталу обылысында жататын аргументтің әр түрлі мәндеріне функцияның да әр түрлі мәндері сәйкес келуі керек.Геометриялық тұрғыдан осы айтылғанға мынадай түсінік беруге болады. Егер абсцисса осіне паралель жүргізілген түзу f функциясының графигін бір нүктеде ғана қиса, онда оның кері функциясы болады.
Егер функцияның графиг ін кем дегенде екі нүктеде қиятын тек бір ғана түзу табылса, онда f - ке кері функция болмайды.

7.Логарифмдік функция
Көрсеткіштік функция ] 0, infinity [ аралығында жатқан мәндерінің әрбіреуін тек бір-ақ рет қабылдайды. Басқаша айтқанда ,кез келген х 0 үшін ау=х теңдігін қанағаттандыратын жалғыз ғана у табылады. Олай болса, көрсеткіштік функцияға кері функция бар болады және оны логарифмдік функция деп аталады да y = f ( x )= logax (x 0 ,a != 1) деп белгіленеді.Көрсеткіштік функция мәндерінің жиыны болатын ] 0 ; infinity [ аралығы логарифмдік функцияның анықталу облысы , ал оның мәндерінің жиын ] - infinity ; infinity [ нақты сандар жиыны болады 1.8 - сурет
Y y=logax(a1)

X
8. Кері тригонометриялық функциялар
Синусты анықтағанда ] - infinity ; infinity [ аралығында жататын sin x - ғана мәні сәйкес келеді дегенбіз. Айнымалылардың тәуелсіздігін кесірінше қарастырғанда тәуелсіз айнымалыға айналған sin x - тің бір мәніне тәуелді айнымалыға айналған х-тің бірнеше мәні сәйкес келеді. Бұл қайшылық оның кері функциясы болмайтындығын көрсетеді. Синусқа кері функция бар болу мүмкіншілігін қамтамасыз ету үшін синус әр түрлі мәндер қабылдай алатындай нақты сандар жиынының бір аралығын бөліп алып қарастырайық. ] - П2 ; П2 [ интервалы осындай аралықтың бірі болсын. Егер және х1 !=х2 болса, онда y1- y2 = sin x1-sin x2=2sin x1-x2 2 cos x1+x2 2!=0. Бұдан синусқа кері функция бар екендігі байқалады және оны arcsin у арқылы белгілейді, яғни х = arcsin у.
Осы сияқты arccos x , arctg x, arcctg x кері функцияларының бар болуын көрсете алады.
Жиі кездесетін өзара кері функциялардың негізгі теңбе-теңдіктерін кесте арқылы берейік:

f [f-1(x)] = x
[f-1 f (x)] = x
1.(x-α)+ α=x
2. xα ∙ α = x
3. αlogαx = x
4.(x1n)n = x
5.sin arcsin x = x
6.cos arccos x = x
7.tg arctg x = x
8.ctg arcctg x = x
(x-α)- α=x
αxα =x
logααx = x
(xn)1n =x (x=0)
arcsin sin x = x (PI2 =x=PI2)
arccos cos x = x (0=x = PI)
arctg tg x = x (-PI2 xPI2)
arcctg ctg x = x (0x PI)

1.3.Шектелген функциялар
Егер А және В сандары табылып, Е жиынының кез келген нүктелерінде мына қос теңсіздіктер
A= f x =B Af x B
Орындалса , онда f- ті Е жиынында шектелген функция деп аталады.Бұл анықтаманы қысқаша былай жазуға болады:
∃ A,B∀x (x∈E--A=f(x)=B -- F функциясы Е жиынында шектелген
делінеді.
Шектелген фунцияның графигі Е жиынының у =А және у=В түзулерінің арасында жатқан жолақта орналасады деп түсіну керек.
1-мысал. У = sin x функциясының шектелгендігін тексеріңдер.
Шешуі. Синус функциясының анықтамасы бойынша
∀x x∈ -infinity,infinity--sinx =1,
А және В сандары тиісінше - 1 мен 1-ге тең.
2-мысал. Тұрақы функция кез келген жиында шектелген.
Шешуі. У x = C тұрақты функция болсын.А=B=C десек, онда 1 - шектелген функция шарты бүкіл нақты сандар жиынында орналасады.Ендеше 2-мысал дұрыс тұжырымдалған.
3-мысал. f x = 1x2 функциясы ] 0 ; 1 [ аралығында шектелмеген функция болатынын көрсету керек.
Шешуі. Бөлу амалы а =0 нүктесінен басқа кез келген нүктелерде орындалады.Ал нолдің аймағында 1x2 С теңсіздігі орындалатындай С саны табу мүмкіншілігі жоқ.Ендеше 0 нүктесінің оң жақ аймағында қарастырылып отырған функция шектелмеген.
6.1-теорема. Егер х --infinity f функциясының шегі бар болса, онда ] N; infinity[ аралығында f функциясы шектелген болады.
Дәлелдеу.Айталық, limx--infinityf x =A болсын.Анықтық үшін ε=1 деп ұйғарадық.Шектің анақтамасы бойынша ε=1 үшін саны табылады да ∀x∈ ]N;infinity [ -- fx -A 1 немесе ∀x∈ ]N;infinity [ -- A-1 fx A+1 шығады.Дәлелдейік деп отырғанымыз да осы еді.

1.5.ФУНКЦИЯНЫҢ АНЫҚТАЛУ ОБЛЫСТАРЫН ТАБУ ЖОЛДАРЫ
х-ті нақты сандар жиынында қарасырсақта элементар функциялардың анықталу облыстары әр түрлі болады.Бұл неге олай болып түр?- деген орынды сұрақ туады. Элементар функцияларды тура xп,аx,sinx және кері ( nx , logax, arcsinx )деп екі класқа бөлуге болады.Тура функциялар нақты сандар жиынында анықталған, ал бұлардың мәндерінің жиынында анықталғандықтан, кері функциялардың анықталу облысы тура функцияға қарағанда өзгеше болады.Арифметикалық амалдардың ішінде бөлу амалының да күрделі функцияның анықталу облысы нақты сандар жиынына өзгеше болуына әсері бар.
Кері амалдардың,кері функциялардың әр қайсысының күрделі анықталу облысына жасайтын әсерін және оны табу жолын алдымен жалпы абстракт функциялар қарастырып, содан айтылған ойымызды мысалдар арқылы түсіндірейк.
Айталық, φx пен ψx функциялары нақты сандар жиынында анықталсын.
1. y= f ( x )=φx ψx функциясы ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.