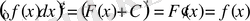Риман мен Стилтьес интегралдары: алғашқы функциялар, анықталмаған интегралдардың қасиеттері және есептеу әдістері


Жоспары
Кіріспе
1. Интеграл ұғымы
2. Алғашқы функция және анықталмаған интеграл ұғымы
3. Анықталмаған интегралдың негізгі қасиеттері
4. Анықталмаған интегралдың кестесі
Кіріспе
Интеграл ұғымы
Риман интегралы ұғымы элементарлы анализ курсында не үзіліссіз, не «аса көп емес» бөлу нүктелері бар функцияларға қолданылатыны белгілі. Өлшенетін функциялар үшін барлық жерде бөлінетіні анықталған болса (немесе абстрактылы аймақта беріліп, оларға үзіліссіздік ұғымы әсер етпесе), интегралдың римандық конструкциясы жарамсыз болып қалады. Осы функцияларына өлшеу теориясының ұқсастығы: Лебег және Стилтьес интегралдары арқылы беріледі. Стилтьес интегралының аса ауқымды функция класын алғандықтан, біз осы интегралды қарастыруға бел будық. Стилтьес интегралын зерттеу барысында Стилтьес интегралдарының бар болу шарттары, оны бөліктеп интегралдауда қолдану және Стилтьес интегралының Риман және геометриялық иллюстрацияларына айрықша мән беру, Стилтьес интегралын анықтау классикалық жағынан ықшам және бірқатар қатынастар ыңғайлы түрде алынғандығын дәлелдеу, Стилтьес интегралын есептеу мәселеріне тоқталу, оның әдістерін зерттеп, мысалдар келтіру арқылы жұмыстың маңыздылығына көз жеткізу.
Лейденск обсерваториясында жұмыс істеп, 1886 жылдан бастап - Тулуза университетінің профессоры болады. Стилтьестің ғылыми ізденістері негізінен функциональды үзіліссіз түбірлер, момент мәселесі, көпмүшелердің ортогональды теориясы, интегралдауға жуықтау және басқа да классикалық анализдің сұрақтарына байланысты болды. Стилтьес интегралының Риман интегралы бойынша жалпы ұғымы қазіргі математикада алатын орны ерекше. Сонымен қатар, Стилтьес алғашқы функциясы да белгілі.
Алғашқы функция және анықталмаған интеграл ұғымы
Дененің қозғалыс заңы S
=S(t)
теңдеуі арқылы берілсін. Мұндағы t- уақыт, S- дененің жүрген жолы. Сонда қарастырылып отырған қозғалыстың берілген мезгілдегі лездік жылдамдығы
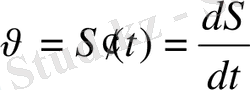 формуласы бойынша анықталатыны бізге дифференциалдық есептеулерден белгілі.
формуласы бойынша анықталатыны бізге дифференциалдық есептеулерден белгілі.
Ал мехеника мен техниканың және тағы басқа көптеген ғылым саласында бұған қарама қарсы мағынадағы есептерді кездестіруге болады. Мысалы, дененің t мезгілдегі жылдамдығы
 беріледі де, сол бойынша дененің қозғалу заңын, яғни өткен уақытпен жүрген жол арасынадағы тәуелділікті анықтау талап етіледі. Бұл есеп дифференциалдық есептеулерде қарастырылған есепке кері есеп екені бізге өзінен өзі түсінікті.
беріледі де, сол бойынша дененің қозғалу заңын, яғни өткен уақытпен жүрген жол арасынадағы тәуелділікті анықтау талап етіледі. Бұл есеп дифференциалдық есептеулерде қарастырылған есепке кері есеп екені бізге өзінен өзі түсінікті.
Сонымен дифференциалдық есептеулерде функция беріліп, оның туындысын талап етіледі. Енді бізге туынды беріледі де, алғашқы туындыны табу талап етіледі.
Анықтама. Егер бір Х аралықтың әрбір нүктесінде F(x) функциясы үшін
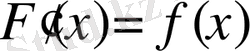 немесе
немесе
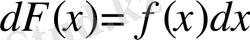 (6. 1. 1)
(6. 1. 1)
теңдігі орындалса, онда F(x) функциясы осы аралықта f(x) үшін алғашқы функция деп аталады.
Сонымен жол, яғни айнымалы функция
S(t) ,
жылдамдық
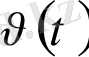 үшін алғашқы функция болады.
үшін алғашқы функция болады.
Мысалы. F(x) =sinx функциясы барлық сан осінде f(x) =cosx функциясының алғашқы функциясы болады, өйткені кез келген
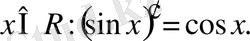
Теорема. Егер F(x) Х аралықта f(x) үшін алғашқы функция болса, онда F(x) +C функциясы да (C- кез келген тұрақты) f(x) үшін осы аралықта алғашқы функция болады.
Дәлелдеу. F(x) функциясы f(x) үшін алғашқы функция. Демек,
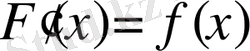 .
.
Сонымен бірге
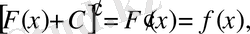 яғни F(x) +C да f(x) функциясына алғашқы функция болады.
яғни F(x) +C да f(x) функциясына алғашқы функция болады.
Дәлелденген теоремадан мынадай қорытынды шығады: егер f(x) функциясы үшін бір алғашқы F(x) табылса, онда оның шексіз көп алғашқы функциялары бар.
Теорема. Берілген функцияның алғашқы функцияларының бір бірінен айырмасы тұрақты шама болады.
Дәлелдеу. Егер берілген f(x) функциясының алғашқы функцияларын F(x)
және Ф(x) десек, онда
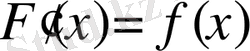 және
және
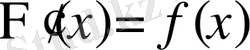 . Олай болса
. Олай болса
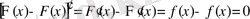
яғни Ф(x) -F(x) =C. Бұдан Ф(x) = F(x) +C (C- кез келген тұрақты) .
Бұл теоремадан мынадай қорытынды шығады: егер F(x) берілген аралықты f(x) -тің алғашқы функцияларының жиыны F(x) +C қосындысымен өрнектеледі. Басқаша айтқанда осы қосындыға кірмейтін оның басқа функциялары болуы мүмкін емес.
Анықтама. Егер F(x) функция f(x) -тің алғашқы функциясы болса, онда барлық алғашқы функцияларының жиынын, яғни F(x) +C өрнегін f(x) -тен анықталмаған интеграл деп атайды және былай белгілейді:
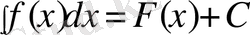
Бұл өрнегі F(x) функциясы f(x) -тің белгілі бір алғашқы функциясы, С-кез келген тұрақты. f(x) -интеграл астындағы функция,
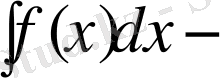 интеграл астындағы өрнек, ал х-интегралдау айнымалысы деп атайды.
интеграл астындағы өрнек, ал х-интегралдау айнымалысы деп атайды.
 ∫− интеграл белгісі.
∫− интеграл белгісі.
Сонымен, қандай да бір функциядан анықталмаған интеграл дегеніміз сол функцияның барлық алғашқы функцияларының жалпы түрі. f(x) -тің алғашқы F(x) +C функцияларының жиынынан белгілі бір алғашқы у функциясын табу үшін x=x 0 болғанда y=y 0 болады деген алғашқы шарт қойылуы керек.
Егер бастапқы шарт берілсе, онда y 0 =F(x 0 ) +C теңдінінен y=F(x) -F(x 0 ) +y 0 түрінде анықталады.
Берілеген f(x) үшін алғашқы F(x) функциясын табу амалы f(x) -ті интегралдау деп аталады.
Туындысы бойынша алғашқы функцияны іздеу, немесе берілген функцияны интегралдау интегралдық есептеулер деп аталады.
Анықталмаған интегралдың негізгі қасиеттері
Дифференциалдау амалына кері амал болып табылатын интегралдау амалын анықтамасына сүйеніп анықталмаған интегралдың мына қасиеттерін дәлелдейік.
- Анықталмаған интегралдың туындысы интеграл астындағы функция, ал дифференцалды интеграл астындағы өрнекке тең болады.
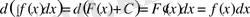
- Дифференциалдың анықталмаған интегралы дифференциалданған функция мен кез келген тұрақтының қосындысына тең, яғни
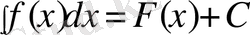
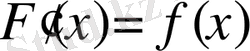 немесе
немесе
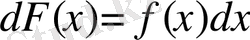
Олай болса,
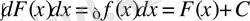
- Тұрақты көбейткішті интеграл белгісінің алдына шығаруға да, интеграл белгісінің астына алып баруға да болады.
Демек
k- тұрақты, теңдіктің екі жағын жеке-жеке алып дифференциалдасақ
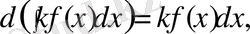
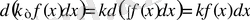
Яғни
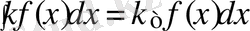 теңдігі дұрыс.
теңдігі дұрыс.
- Бірнеше фнукциалардың алгебралық қосындысының анықталмаған интегралы қосылғыштардан алынған анықталмаған интегралдың алгебралық қосындысына тең, яғни
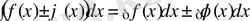
Бұл теңдік те алдыңғы теңдікті дәлелдегендей дәлелденеді.
- Егер F(x) функциясы f(x) үшін алғашқы функция болса, онда
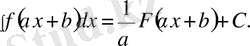
Дәлелдеу.
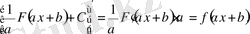
Анықталмаған интегралдың кестесі
Егер U=U(x) белгілі бір Х аралықта дифференциалданатын функция болса, дифференциялдық есептеулердің формулаларын еске алып анықталмаған интегралдың негізгілерін мынадай кестесін жасауға болады.
1)
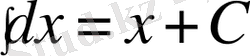
2)
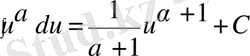 (α≠-1, кез келген сан) .
(α≠-1, кез келген сан) .
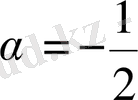 болса, онда
болса, онда
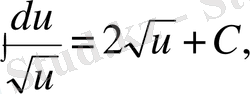
 болса, онда
болса, онда
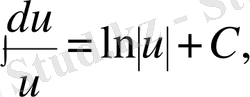
 болса, онда
болса, онда
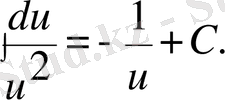
3)
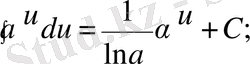
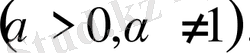
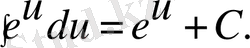
4)
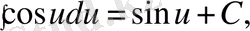
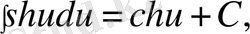
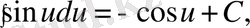

5)
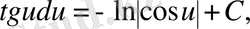
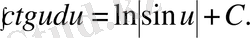
6)
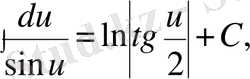
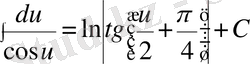
7)
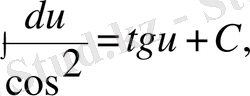
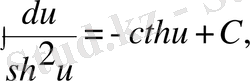
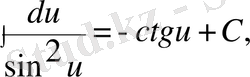
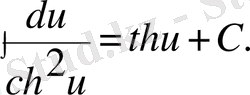
8)
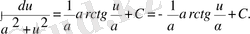
9)
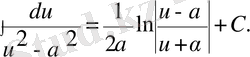
10)
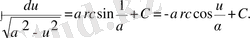
11)
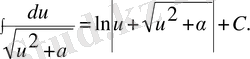
Бұл кестеге енген әрбір формуланың дұрыстығын дифференциалдау арқылы дәлелдеуге болады.
Осы таблицадағы формулалармен бірге мына интегралдарды да білген дұрыс;
12)
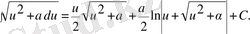
13)
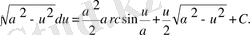
14)
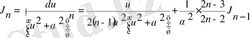
15)
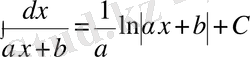
16)
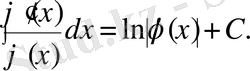
17)
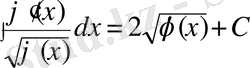
Бұл интегралдарды бір соңғы параграфтарда дәлелдейміз.
Тікелей интегралдау. Айнымалыны ауыстыру және бөліктен интегралдау
Көптеген функциялардың анықталмаған интегралдың таблицадағы формулалар мен негізгі қасиеттерге сүйеніп бірден жазуға болады . Тікелей интегралдау дегеніміз осы.
Бірнеше мысалдар келтірейік.
1-мысал.
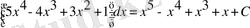
2-мысал.
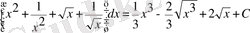
Бұл мысалдарда біз 3-ші, 4-ші қасиеттерді және 1-ші, 2-ші формулаларды пайдаландық.
3-мысал.
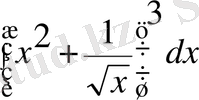 интегралын есептеу керек.
интегралын есептеу керек.
Шешуі: Екі мүшелікті үшінші дәрежеге шығарамыз да, әрбір қосылғышты дәреже түрінде жазамыз, сонан кейін 3-ші және 4-ші қасиеттерді пайдалана отырып, 2-ші формуланы қолдансақ, мынау шығады:
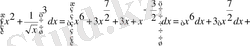
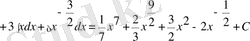
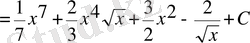
4-мысал.
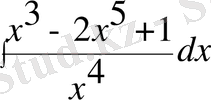 интегралын есептеу керек.
интегралын есептеу керек.
Шешуі: Интеграл астындағы функцияның алымын бөліміне мүшелеп бөлеміз де, сонан кейін 3-ші, 4-ші қасиеттер мен 2-ші формуланы қолданамыз. Сонда:
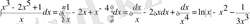
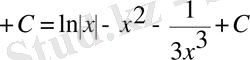 болады.
болады.
Ескерту. Әрбір қосылғыштың соңында ерікті тұрақтыны жазып жатудың қажеті жоқ, өйткені ерікті тұрақтылардың қосындысы да ерікті тұрақты болады, сондықтан оны біз соңында жазамыз.
5-мысал.
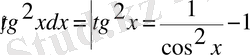 болғандықтан
болғандықтан

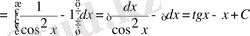
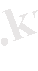
Біз бұл жерде 7-ші және 1-ші формулалармен 4-ші қасиетті пайдаландық.
6-мысал.
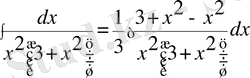 .
.
Соңғы интегралды екі интегралдың айырымы түрінде жазып алып формулалар мен қасиеттердің көмегімен интегралдасақ,
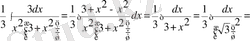
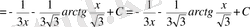 болады.
болады.
7-мысал.
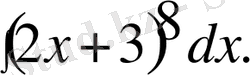
Шешуі:
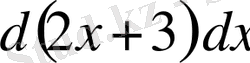 немесе
немесе
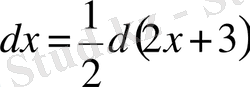 екенін ескерсек, берілген интегралды былайша жазуға болады:
екенін ескерсек, берілген интегралды былайша жазуға болады:
Енді бұған 2-ші формуланы немесе 5-қасиетті қолдансақ
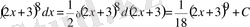 болып шығады.
болып шығады.
8- мысал.
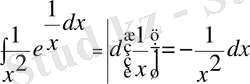 екенін ескерсек
екенін ескерсек

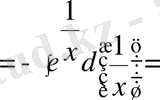 3-ші формула бойынша=
3-ші формула бойынша=
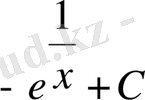
Айнымалыны ауыстыру әдісі мына формуланы қолдануға негізделген
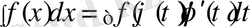 (6. 4. 1)
(6. 4. 1)
Анықталмаған интегралдың анықтамасы бойынша
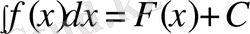
Егер х тәуелсіз айнымалы болса, онда dF(x) =f(x) dx теңдігі орындалатынын және бірінші ретті дифференциал формуласының инватианттығын еске алып х айнымалыдан
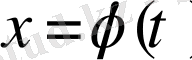 формула бойынша t-ға көшкен жағдайда
формула бойынша t-ға көшкен жағдайда
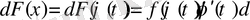 теңдігі орындалады. Енді осы теңдіктің екі жағынан интеграл алсақ (6. 4. 1) теңдігі шығады.
теңдігі орындалады. Енді осы теңдіктің екі жағынан интеграл алсақ (6. 4. 1) теңдігі шығады.
Осы формулаға мысал келтірейік.
9-мысал.
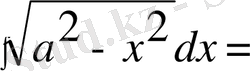 х айнымалыны
х айнымалыны
 деп алған тиімді. Бұдан
деп алған тиімді. Бұдан
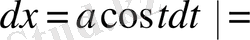
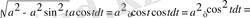
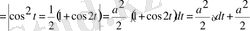
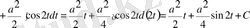
Осы шыққан нәтижені бұрынғы тәуелсіз айнымалы х арқылы өрнектейік. Яғни
 немесе
немесе
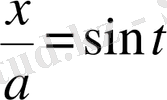 теңдігінен
теңдігінен
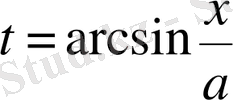 болады. Сонда
болады. Сонда
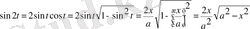
Болып өрнектеледі.
Демек,
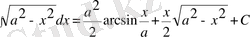
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz