Зееман және Штарк эффектілері: атом энергетикалық деңгейлерінің магнит және электр өрістеріндегі жіктелуі мен спектрлік ығысуы


Мазмұны
Кіріспе . . . 4
1. 1 Атомдар мен молекулалардың сыртқы магнит және электр өрістерімен әсерлесуі. 5
1. 2 Зееман эффектісі. . 6
1. 3 Штарк эффектісі19
2. 1 Магниттік резонанс23
2. 2 Молекулалардың құрылысы мен қасиеттері. 34
Қорытынды 60
Қолданылған әдебиеттер тізімі . . 61
Кіріспе
Жұмыстың мақсаты: Атомның магниттік моменті және оның кеңістіктік квантталуының болатынына Зееман құбылысы ең бір тәжірибелік дәлел болып табылады. Зееманның күрделі немесе аномаль құбылысында спектрлік сызықтар үштен көп құраушыға жіктеледі. Жүргізілген зерттеулер қарапайым Зееман құбылысының тек синглеттік спектрлік сызықтарда байқалатындығын көрсетеді. Зееманның күрделі құбылысы жағдайында сілтілік элемент атомдары бас сериясының дублет сызықтарын өріске перпендикуляр бағытта бақыласа, онда дублеттің бір сызығы төрт сызыққа, ал екіншісі алты сызыққа жіктеледі.
Алға қойылған мақсаттарға жету үшін шешілетін зерттеу міндеттері: Атомдық физика курсында Зееман құбылысын атомның векторлық моделін пайдаланып түсіндіреміз. Ал бұл құбылыстың қатаң теориясын релятивтік кванттық механика жәрдемімен ғана түсіндіруге болатындығын айтуға болады. Атомның толық импульс моменті, мұнымен байланысқан магниттік моменті болатындығы ғылымда бұрын қарастырылған. Қарапайым Зееман құбылысымен нәзік түзілісі жоқ спектрлік сызықтардың Зеемандық жіктелуін қарастыруға болады.
Зерттеу нысаны: Зееман және Штарк эффектісін пайдаланып атом шығаратын жарықтың жиілігімен поляризациясына магнит өрісінің ғана емес, сонымен қатар электр өрісінің болатындығын да айтуға болады. Бұл құбылысты сутегі спектрін зерттеу кезінде Штарк бақылаған. Атомға электр өрісі әсер етіп, оны поляризациялайды, яғни оң зарядталған ауыр ядроға қатысты электрондарды ығыстырады. Нәтижеде атомда дипольдық момент пайда болады, ол өріспен әсерлесіп, жүйе энергиясының өзгеруін туғызады.
Жұмыстың ғылыми жаңалығы: Штарк және Зееман эффектісіне сәйкес атомдар соқтығысқан кезде деңгейлердің орны атомды қоршап тұрған бөлшектердің өрістері әсерінен өзгеруге мүмкін екендігі байқалады. Электр өрісінің атомға әсерінің тағы бір көрінісі спектрде тиым салынғандарға жататын жаңа бір сызықтың пайда болуы. Электр өрісі ықпалынан пайда болатын электрлік дипольдық момент кванттық сандары әр түрлі күйлер үшін әр түрлі болады.
Жұмыстың тәжірибелік құндылығы: Орта мектепте атом және ядро физикасына байланысты тақырыптарды талдауда Зееман және Штарк эффектілерін пайдаланып түсіндіру қазіргі заман физикасына сәйкес келеді. Осы мәселе диссертациялық жұмыстың тәжірибелік құндылығы болып табылады.
Атомдар мен молекулалардың сыртқы магнит және электр өрістерімен әсерлесуі.
Егер атом не молекула сыртқы электр не магнит өрісіне орналастырылған болса, онда бұлардың энергия деңгейлері өзгереді. Энергетикалық деңгейлердің жіктелуі мен ығысуы магнит өрісі әсерінен болса, онда ол Зееман эффекті деп, ал электр өрісі әсерінен болса, онда Штарк эффекті деп аталады. Алғаш бұл құбылыстар спектрлік сызықтардың магнит өрісі әсерінен (П. Зееман, 1896) жіктелуі түрінде және электр өрісі әсерінен (И. Штарк, 1913) жіктелуі түрінде байқалған. Қазіргі кезде Зееман және Штарк құбылыстарына магнит не электр өрісіндегі спектрлік сызықтардың жіктелуі ғана емес, бұларға қоса энергетикалық деңгейлердің бірнеше деңгейшелерге жіктелуі мен ығысуы да жатқызылады.
Квантмеханикалық тұрғыдан бұл құбылыстардың мәнісі мынада. Егер атом біртекті электр не магнит өрісіне орналастырылса, онда оқшау
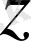 бағыты пайда болады: электрондар енді сфералық симметриялы емес, аксиал симметриялы өрісте қозғалады. Осыдан атомның
бағыты пайда болады: электрондар енді сфералық симметриялы емес, аксиал симметриялы өрісте қозғалады. Осыдан атомның
 толық импульс моменті енді сақталмайды. Сыртқы өріс бағытына толық моменттің
толық импульс моменті енді сақталмайды. Сыртқы өріс бағытына толық моменттің
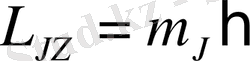 проекциясы сақталатын болады. Сондықтан
проекциясы сақталатын болады. Сондықтан
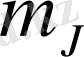 мәндері әр түрлі күйлердің энергиясы әр түрлі болады, яғни сыртқы магнит не электр өрісі әсерінен деңгейдің азғындалуы жойылады-деңгей жіктеледі.
мәндері әр түрлі күйлердің энергиясы әр түрлі болады, яғни сыртқы магнит не электр өрісі әсерінен деңгейдің азғындалуы жойылады-деңгей жіктеледі.
Кулондық өрісте (релятивтік емес жуықтауда) электронның барлық энергетикалық деңгейлері азғындалған-энергия тек
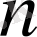 бас кванттық санға тәуелді де,
бас кванттық санға тәуелді де,
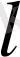 орбиталық кванттық санға тәуелсіз. Осы себепті сутегі атомының энергетикалық деңгейлері
орбиталық кванттық санға тәуелсіз. Осы себепті сутегі атомының энергетикалық деңгейлері
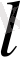 бойынша азғындалған болады. Сілтілік металл атомдарын енді электроны кулондық емес, орталық симметриялы өрісте қозғалатын, бір электронды атом ретінде қарастыру керек. Мұнда
бойынша азғындалған болады. Сілтілік металл атомдарын енді электроны кулондық емес, орталық симметриялы өрісте қозғалатын, бір электронды атом ретінде қарастыру керек. Мұнда
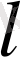 бойынша азғындалу жойылады-деңгей энергиясы тек
бойынша азғындалу жойылады-деңгей энергиясы тек
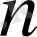 -ге емес
-ге емес
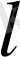 -ге де тәуелді.
-ге де тәуелді.
Сілтілік металл атомдары спектрлік серияларының ерекшелігі осыған байланысты. Ал спин-орбиталық әсерлесу спектрлік сызықтардың нәзік түзілісін тудырады. Бірақ сыртқы өрістер жоқ кезде кеңістіктегі барлық бағыт біріне-бірі пара-пар болатындықтан, деңгейлердің энергиялары
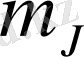 магниттік кванттық санға тәуелсіз. Бұл
магниттік кванттық санға тәуелсіз. Бұл
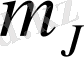 кванттық саны
кванттық саны
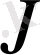 берілгенде
берілгенде
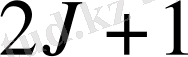 мән қабылдай алатындығына қарамастан болады. Осыған сәйкес азғындалу, сонымен
мән қабылдай алатындығына қарамастан болады. Осыған сәйкес азғындалу, сонымен
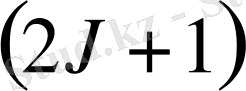 -ге тең. Магнит өрісі осы азғындалуды жояды: әрбір энергетикалық деңгей
-ге тең. Магнит өрісі осы азғындалуды жояды: әрбір энергетикалық деңгей
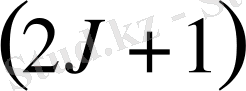 деңгейшеге жіктеледі. Зееман құбылысы осылай түсіндіріледі. Зееман құбылысы қарапайым және күрделі болып бөлінеді. Бірақ электрон спині ашылғанға дейін Зееманның қарапайым құбылысын ғана түсіндіру мүмкін болды.
деңгейшеге жіктеледі. Зееман құбылысы осылай түсіндіріледі. Зееман құбылысы қарапайым және күрделі болып бөлінеді. Бірақ электрон спині ашылғанға дейін Зееманның қарапайым құбылысын ғана түсіндіру мүмкін болды.
Зееман эффекті
Атомның магниттік моменті және оның кеңістіктік квантталуының болатындығына Зееман құбылысы ең бір сенімді тәжірибелік дәлел болып табылады.
Тәжірибелік заңдылықтар. Магнит полюстері аралығына жарық көзін орналастырып оның спектрін ажыратқыш қабілеті жоғары құрал арқылы зерттегенде спектрлік сызықтардың жіктелетіндігі тағайындалған. Сонда қалыпты немесе қарапайым зееман құбылысы жағдайында жарық көзі шығаратын жарықты магнит өрісіне перпендикуляр бағытта бақылағанда, әрбір сызықтың
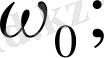
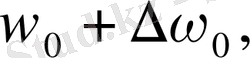
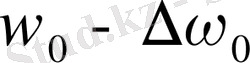 үш сызыққа жіктелетіндігі байқалады; мұндағы
үш сызыққа жіктелетіндігі байқалады; мұндағы
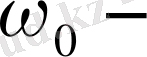 магнит өрісі жоқ кездегі сызық жиілігі,
магнит өрісі жоқ кездегі сызық жиілігі,
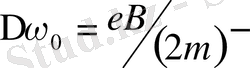 жиіліктің лоренцтік ығысуы. Ал жарық көзінің сәулесін магнит өрісіне параллель бағытта бақылағанда әрбір сызық тек
жиіліктің лоренцтік ығысуы. Ал жарық көзінің сәулесін магнит өрісіне параллель бағытта бақылағанда әрбір сызық тек
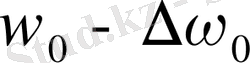 ,
,
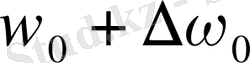 екі құраушы сызыққа жіктеледі. (1. 1-сурет) . Бұлардың әрқайсысы дөңгелек поляризацияланған:
екі құраушы сызыққа жіктеледі. (1. 1-сурет) . Бұлардың әрқайсысы дөңгелек поляризацияланған:
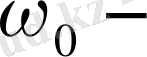 ден қызыл жаққа ығысқаны - оң дөңгелектік, ал күлгін жаққа ығысқаны - сол дөңгелектік поляризацияланған.
ден қызыл жаққа ығысқаны - оң дөңгелектік, ал күлгін жаққа ығысқаны - сол дөңгелектік поляризацияланған.
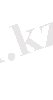 Өріске перпендикуляр бағытта сәулені бақылағанда үш сызықтық поляризацияланған сызық байқалады: біреуі ығыспаған, мұның поляризация векторы
Өріске перпендикуляр бағытта сәулені бақылағанда үш сызықтық поляризацияланған сызық байқалады: біреуі ығыспаған, мұның поляризация векторы
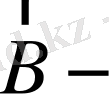 ға параллель және екі ығысқан (әрқайсысы
ға параллель және екі ығысқан (әрқайсысы
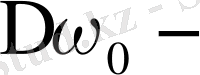 ға), бұлардың поляризация векторлары
ға), бұлардың поляризация векторлары
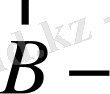 ға перпендикуляр. Ығысқан дөңгелек (
ға перпендикуляр. Ығысқан дөңгелек (
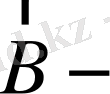 мен бағыттас сәуле), не сызықты (
мен бағыттас сәуле), не сызықты (
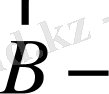 ға перпендикуляр сәуле) поляризацияланған сызықтар
ға перпендикуляр сәуле) поляризацияланған сызықтар
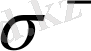 және
және
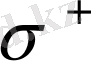 құраушы деп аталады. Сызықты поляризацияланған (
құраушы деп аталады. Сызықты поляризацияланған (
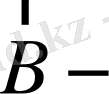 ға перпендикуляр сәуле) ығыспаған сызық
ға перпендикуляр сәуле) ығыспаған сызық
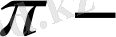 құраушы,
құраушы,
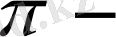 поляризацияланған фотондар өріске перпендикуляр бағытта ғана шығарылады.
поляризацияланған фотондар өріске перпендикуляр бағытта ғана шығарылады.
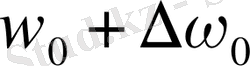
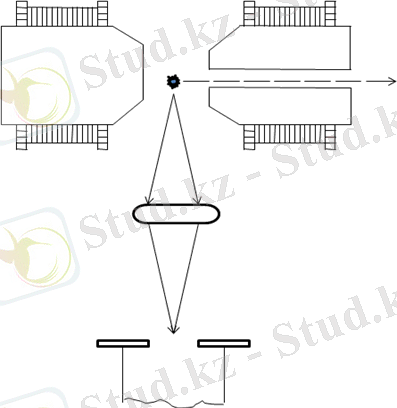
1. 1-сурет
Зееманның күрделі немесе аномаль құбылысында спектрлік сызықтар үштен көп құраушыға жіктеледі және
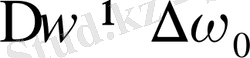 . Жүргізілген зерттеулер қарапайым Зееман құбылысының тек синглеттік спектрлік сызықтарда байқалатындығын көрсетті. Мультиплеттегі синглет емес барлық сызықтар үшін күрделі Зееман құбылысы байқалады.
. Жүргізілген зерттеулер қарапайым Зееман құбылысының тек синглеттік спектрлік сызықтарда байқалатындығын көрсетті. Мультиплеттегі синглет емес барлық сызықтар үшін күрделі Зееман құбылысы байқалады.
Өріс жоқта мультиплеттік сипаттағы (дублет, триплет және т. т. ) спектрлік сызықтар үшін күрделі Зееман құбылысы байқалады. Әлсіз өрісте әдеттегі зеемандық триплет орнына спектрлік сызықтың күрделірек түзілісі алынады.
Мәселен, Зееманның күрделі құбылысы жағдайында сілтілік элемент атомдары бас сериясының дублет сызықтарын өріске перпендикуляр бағытта бақыласа, онда дублеттің бір сызығы 4 сызыққа, ал екіншісі - 6 сызыққа жіктеледі. Демек, бұл жағдайда 10 спектрлік құраушы байқалады. Мультиплеттердің жеке сызықтары жиілігінің күрделі Зееман құбылысындағы
 ығысуы
ығысуы
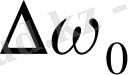 Лоренцтік ығысу өрнегін қанағаттандырмайды. Рунге ережесіне сәйкес
Лоренцтік ығысу өрнегін қанағаттандырмайды. Рунге ережесіне сәйкес
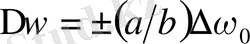 , мұндағы
, мұндағы
 және
және
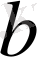 -Рунге коэффициенттері, бүтін кіші сандар. Мәселен, сілтілік элемент атомдарының бас сериясы дублеттерінің жіктелуі үшін
-Рунге коэффициенттері, бүтін кіші сандар. Мәселен, сілтілік элемент атомдарының бас сериясы дублеттерінің жіктелуі үшін
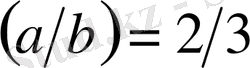 ,
,
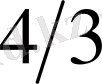 (дублеттің ұзын толқынды сызығы үшін) және
(дублеттің ұзын толқынды сызығы үшін) және
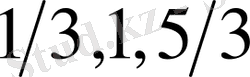 (қысқа толқынды сызық үшін) .
(қысқа толқынды сызық үшін) .
Тағы бір тәжірибелік дерек Престон ережесі деп аталады. Осыған сәйкес, жіктелу еселігі және
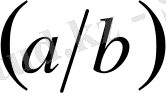 Рунге коэффициенттері берілген сызық жиілігіндегі фотондарды шығарып көшкендегі атомның бастапқы және аяққы күйлерін сипаттайтын
Рунге коэффициенттері берілген сызық жиілігіндегі фотондарды шығарып көшкендегі атомның бастапқы және аяққы күйлерін сипаттайтын
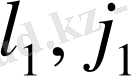 және
және
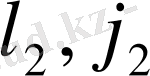 кванттық сандарына тәуелді, бірақ осы күйлердің
кванттық сандарына тәуелді, бірақ осы күйлердің
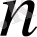 бас кванттық санына тәуелді емес. Сонымен, берілген серияның барлық сызықтары күрделі Зееман эффектісінде бірдей жіктеледі. Қарапайым Зееман құбылысының теориясын 1896 ж. Лоренц Г. классикалық физика заңдары негізінде ұсынды. Лоренц теориясы қарапайым құбылыс жағдайында сызықтардың магнит өрісіндегі жіктелу сипатын түсіндіріп берді. Бұл теория тәжірибемен жақсы үйлесетін нәтижелер берумен қатар, зеемандық құраушылардың поляризациялық сипатын да болжап берді. Бұл да тәжірибеде расталды. Бірақ Лоренц теориясы күрделі Зееман құбылысын түсіндіре алмады.
бас кванттық санына тәуелді емес. Сонымен, берілген серияның барлық сызықтары күрделі Зееман эффектісінде бірдей жіктеледі. Қарапайым Зееман құбылысының теориясын 1896 ж. Лоренц Г. классикалық физика заңдары негізінде ұсынды. Лоренц теориясы қарапайым құбылыс жағдайында сызықтардың магнит өрісіндегі жіктелу сипатын түсіндіріп берді. Бұл теория тәжірибемен жақсы үйлесетін нәтижелер берумен қатар, зеемандық құраушылардың поляризациялық сипатын да болжап берді. Бұл да тәжірибеде расталды. Бірақ Лоренц теориясы күрделі Зееман құбылысын түсіндіре алмады.
Зееман құбылысының түсіндірілуі. Атомдық физика курсында Зееман құбылысын атомның векторлық моделін пайдаланып түсіндіреміз. Ал бұл құбылыстың қатаң теориясын релятивтік кванттық механика жәрдемімен ғана құруға болатындығын ескерте кетейік.
Магнит өрісі жоқ кезде атом энергиясы
 қайсыбір күйде тұрған болсын. Осы атомды индукциясы
қайсыбір күйде тұрған болсын. Осы атомды индукциясы
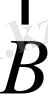 магнит өрісіне орналастырамыз. Магнит өрісін әлсіз, яғни
магнит өрісіне орналастырамыз. Магнит өрісін әлсіз, яғни
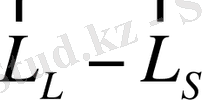 байланысы
байланысы
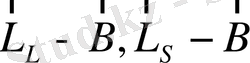 байланыстарына қарағанда күштірек деп есептейміз. Демек,
байланыстарына қарағанда күштірек деп есептейміз. Демек,
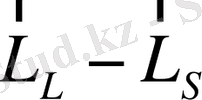 әсерлесуі бұзылмаған. Бұл шектеу магнит өрісінің әлсіз болуының физикалық белгісі. Магнит өрісіндегі атом энергиясы магнит өрісімен атомның магниттік моментінің әсерлесуі нәтижесінде өзгеретін болады. Сонда атом энергиясы мынаған тең болады:
әсерлесуі бұзылмаған. Бұл шектеу магнит өрісінің әлсіз болуының физикалық белгісі. Магнит өрісіндегі атом энергиясы магнит өрісімен атомның магниттік моментінің әсерлесуі нәтижесінде өзгеретін болады. Сонда атом энергиясы мынаған тең болады:
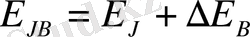 (1)
(1)
Атомның толық импульс моменті (бұрыштық моменті)
 , мұнымен байланысқан магниттік моменті
, мұнымен байланысқан магниттік моменті
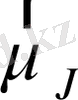 болатындығы бұрын қарастырылған болатын. Егер
болатындығы бұрын қарастырылған болатын. Егер
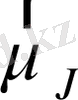 магниттік моментке ие магниттік диполь тұрақты магнит өрісіне орналастырылсса, онда диполь энергиясы оның өріске қатысты бағдарлануына тәуелді болады. Индукциясы
магниттік моментке ие магниттік диполь тұрақты магнит өрісіне орналастырылсса, онда диполь энергиясы оның өріске қатысты бағдарлануына тәуелді болады. Индукциясы
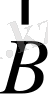 өрістегі дипольдің осы бағдарлану энергиясы мынаған тең:
өрістегі дипольдің осы бағдарлану энергиясы мынаған тең:
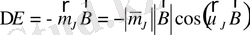 (2)
(2)
 векторының, демек
векторының, демек
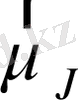 векторының да
векторының да
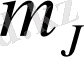 кванттық санымен анықталатын тек белгілі бағдарлануы болады. Осыған сәйкес атомның бағдарлану энергиясы дискретті мәндер қабылдайды.
кванттық санымен анықталатын тек белгілі бағдарлануы болады. Осыған сәйкес атомның бағдарлану энергиясы дискретті мәндер қабылдайды.
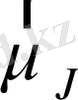 шамасын анықтайық.
шамасын анықтайық.
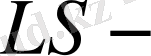 жуықтауында атомға
жуықтауында атомға
 орбиталық және
орбиталық және
 спиндік импульс моменттері таңылады:
спиндік импульс моменттері таңылады:
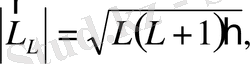

Бұларға жалпы атомның орбиталық магниттік моменті:
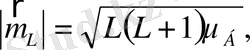 (3)
(3)
және жалпы атомның спиндік магниттік моменті:
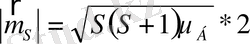 (4)
(4)
сәйкес келеді. Мұндағы
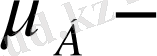 Бор магнетоны, бұл магниттік моменттің бірлігі.
Бор магнетоны, бұл магниттік моменттің бірлігі.
Атомның
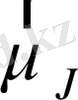 толық магниттік моменті
толық магниттік моменті
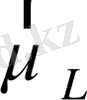 және
және
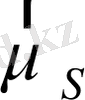 моменттерінің векторлық қосындысына тең:
моменттерінің векторлық қосындысына тең:
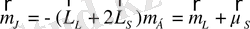 (5)
(5)


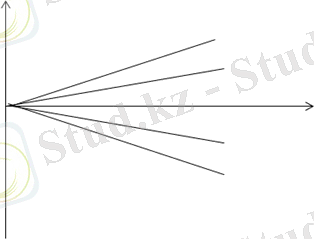
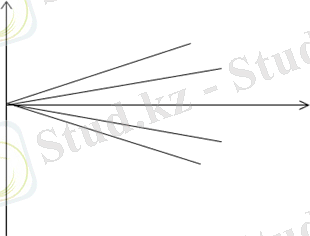


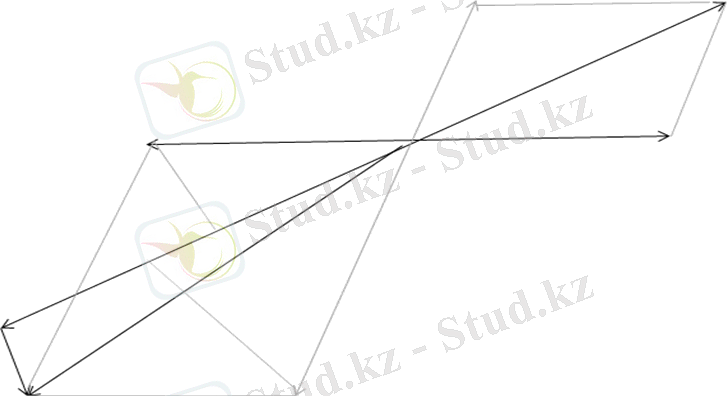
1. 2-сурет
Электрон заряды теріс болғандықтан, мұнда минус таңбасы қойылған. Тағы айтатын нәрсе, орбиталық моментке қарағанда спиндік моментке екі есе үлкен магниттік момент сәйкес келеді. [(4) және (5) өрнектеріндегі 2 көбейткіші спиннің гиромагниттік қатынасының аномалиясынын салдары] . Осы себептен жалпы жағдайда атомның
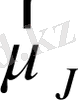 толық магниттік моменті оның
толық магниттік моменті оның
 толық механикалық моментіне 1. 2-суретте көрсетілгендей антипараллель болмайды.
толық механикалық моментіне 1. 2-суретте көрсетілгендей антипараллель болмайды.
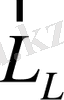 және
және
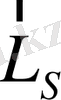 векторлары бір-бірінен толық тәуелсіз емес, өйткені бұларқосылып квантталған
векторлары бір-бірінен толық тәуелсіз емес, өйткені бұларқосылып квантталған
 толық момент беруге тиіс. Осыған ұқсас
толық момент беруге тиіс. Осыған ұқсас
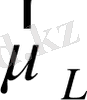 және
және
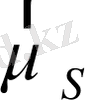 векторлары да бір-бірімен байланысқан болуға тиіс. Сонда бұлар қосылып атомның толық магниттік моментін беретін болады.
векторлары да бір-бірімен байланысқан болуға тиіс. Сонда бұлар қосылып атомның толық магниттік моментін беретін болады.
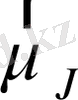 магниттік момент
магниттік момент
 толық механикалык моментпен мына қатынаспен байланысқан:
толық механикалык моментпен мына қатынаспен байланысқан:
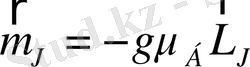 (6)
(6)
мұндағы өлшемділіксіз коэффицент
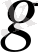 , Ланде факторы немесе көбейткіші деп аталады. Ол
, Ланде факторы немесе көбейткіші деп аталады. Ол
 векторы түзілгенде
векторы түзілгенде
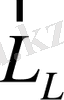 және
және
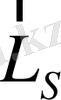 векторларының қалайша комбинациялануына қарай, нөлден екіге дейінгі әр түрлі мәндер қабылдай алады.
векторларының қалайша комбинациялануына қарай, нөлден екіге дейінгі әр түрлі мәндер қабылдай алады.
Ланде факторы
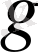 . 1. 2б-суретте көрсетілген атомның векторлық моделінің көмегімен
. 1. 2б-суретте көрсетілген атомның векторлық моделінің көмегімен
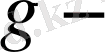 факторын есептеуге болады. (6) өрнекке сәйкес
факторын есептеуге болады. (6) өрнекке сәйкес
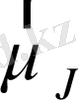 толық магниттік момент
толық магниттік момент
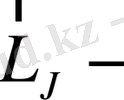 ге коллинеар болуға тиіс. Бірақ
ге коллинеар болуға тиіс. Бірақ
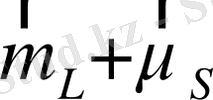 қосындысы осы талапты қанағаттандырмайды. Атомның векторлық моделіне сәйкес
қосындысы осы талапты қанағаттандырмайды. Атомның векторлық моделіне сәйкес
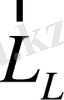 және
және
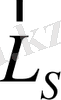 векторлары, демек,
векторлары, демек,
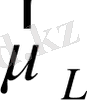 және
және
 векторлары да
векторлары да
 векторын тез айнала қозғалады. Сонда магнитік моменттердің
векторын тез айнала қозғалады. Сонда магнитік моменттердің
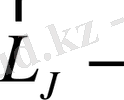 ге перпендикуляр құраушылары период бойынша орташа алғанда нөлге тең
ге перпендикуляр құраушылары период бойынша орташа алғанда нөлге тең
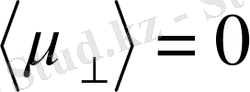 . Сондықтан атомның
. Сондықтан атомның
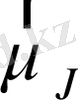 толық магниттік моменті тек
толық магниттік моменті тек
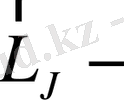 ге параллель құраушылармен анықталады, яғни:
ге параллель құраушылармен анықталады, яғни:
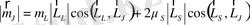 (7)
(7)
ABC үшбұрышының a және b қабырғалары арасындағы бұрыштың косинусын
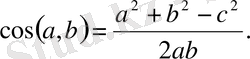
пайдаланып,
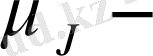 ді табамыз:
ді табамыз:
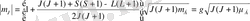
осыдан
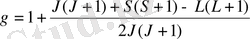 (8)
(8)
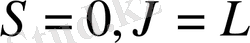 болғанда (толық моментті таза орбиталық момент тудырады)
болғанда (толық моментті таза орбиталық момент тудырады)
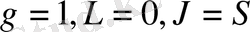 болғанда (толық момент таза спиндік моментке тең)
болғанда (толық момент таза спиндік моментке тең)
 жалпы жағдайда
жалпы жағдайда
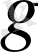 нөлден екіге дейінгі әр түрлі мәндерді қабылдай алады.
нөлден екіге дейінгі әр түрлі мәндерді қабылдай алады.
Энергетикалық деңгейлердің магнит өрісінде жіктелуі.
Магниттік моменттің өріс бағытына ұлықсат етілген проекциялары
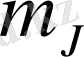 кванттық санымен анықталады. Осылай болғандықтан (2) формуланы пайдаланып энергетикалық жіктелу шамасын табамыз:
кванттық санымен анықталады. Осылай болғандықтан (2) формуланы пайдаланып энергетикалық жіктелу шамасын табамыз:
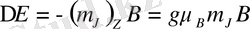 (9)
(9)
Сыртқы өріс бағытымен дәл келетін
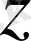 осіне
осіне
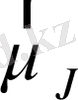 векторының ұлықсат етілген проекциялары (6) қатынасын қанағаттандырады.
векторының ұлықсат етілген проекциялары (6) қатынасын қанағаттандырады.
Сонымен, магнит өрісі деңгейді 1. 2-суретте көрсетілгендей
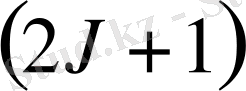 құраушыға жіктелуін тудырып, деңгейдің азғындалуын толығынан жояды (егер тек
құраушыға жіктелуін тудырып, деңгейдің азғындалуын толығынан жояды (егер тек
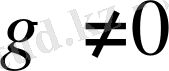 ) . Осындай жіктелуді зеемандық жіктелу, ал бұған сәйкес деңгейлерді зеемандық деңгейлер деп атайды.
) . Осындай жіктелуді зеемандық жіктелу, ал бұған сәйкес деңгейлерді зеемандық деңгейлер деп атайды.
(9) өрнегімен және 1. 2а-суреттен зеемандық жіктелудің сыртқы магнит өрісіне пропорционал екендігін көруге болады. Осы сызықтық тәуелділік әлсіз магнит өрістерінде ғана сақталады. Сонда әлсіз деп саналатын магнит өрісіндегі
 жіктелу шамасы табиғи мультиплеттік жіктелу шамасынан елеулі кіші болады. Ал күшті магнит өрістерінде
жіктелу шамасы табиғи мультиплеттік жіктелу шамасынан елеулі кіші болады. Ал күшті магнит өрістерінде
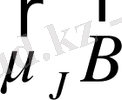 көбейтіндісі (магниттік жіктелу шамасы) ұйтқымаған атомның көрші энергия деңгейлерінің ара қашықтығына шамалас болады да деңгейлердің жіктелуі (9) формуласынан өзгеше болады.
көбейтіндісі (магниттік жіктелу шамасы) ұйтқымаған атомның көрші энергия деңгейлерінің ара қашықтығына шамалас болады да деңгейлердің жіктелуі (9) формуласынан өзгеше болады.
Атомның магниттік моментінің сыртқы магнит өрісімен әсерлесуінің
 потенциалдық энергиясы (9) өрнегімен анықталады:
потенциалдық энергиясы (9) өрнегімен анықталады:
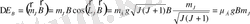
мұндағы
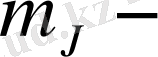 толық магниттік кванттық сан, ол
толық магниттік кванттық сан, ол
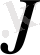 берілгенде
берілгенде
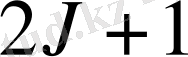 мән қабылдайды, яғни
мән қабылдайды, яғни
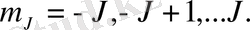
Сонымен (1), (9) өрнектеріне сәйкес әлсіз магнит өрісінде атомның әрбір
 энергетикалық деңгейі энергиялары
энергетикалық деңгейі энергиялары
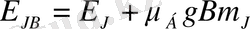 (10)
(10)
болатын
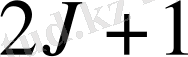 деңгейшеге жіктеледі. Атомның энергетикалық деңгейлерінің магнит өрісі әсерінен жіктелуін зеемандық жіктелу деп атайды.
деңгейшеге жіктеледі. Атомның энергетикалық деңгейлерінің магнит өрісі әсерінен жіктелуін зеемандық жіктелу деп атайды.
Сыртқы магнит өрісінде атомның энергетикалық деңгейлерінің жіктелуінен спектрде жаңа сызықтар пайда болады. Енді осыған көз жеткізейік.
Магнит өрісі жоқта атом
 күйден
күйден
 күйге көшіп, жиілігі
күйге көшіп, жиілігі
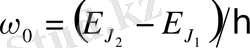 сызық шығаратын болсын. Магнит өрісінде
сызық шығаратын болсын. Магнит өрісінде
 және
және
 күйлерінде (10) өрнегіне сәйкес атом энергиясы былай анықталатын болады:
күйлерінде (10) өрнегіне сәйкес атом энергиясы былай анықталатын болады:
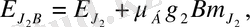
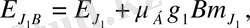
яғни деңгейлер
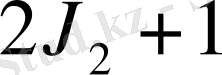 және
және
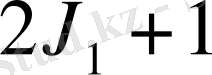 деңгейшелерге жіктеледі. Демек, магнит өрісінде атом
деңгейшелерге жіктеледі. Демек, магнит өрісінде атом
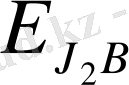 күйден
күйден
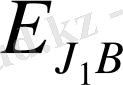 күйге көшкен кезде мына жиіліктердегі сәуле шығарылады:
күйге көшкен кезде мына жиіліктердегі сәуле шығарылады:
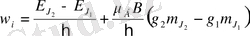
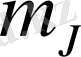

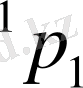
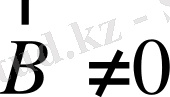 немесе
немесе
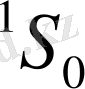
1. 3-сурет
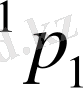
(11)
мұндағы
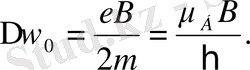
(11) өрнегінен сыртқы магнит өрісі әсерінен атомның энергетикалық деңгейлерінің жіктелуі спектрде жаңа сызықтарды тудыратындығы келіп шығады.
Қарапайым Зееман құбылысы.
Алдымен нәзік түзілісі жоқ (синглет) спектрлік сызықтардың зеемандық жіктелуін қарастырайық. Мұндай сызықтар қарапайым синглет деңгейлер (яғни толық спин
 ) арасындағы көшулер нәтижесінде пайда болады. Осындай деңгейлер үшін
) арасындағы көшулер нәтижесінде пайда болады. Осындай деңгейлер үшін
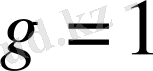 . Демек, (9) формуласы мына түрге келеді:
. Демек, (9) формуласы мына түрге келеді:
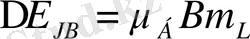 (12)
(12)
Өйткені
 болғандықтан,
болғандықтан,
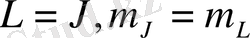 болады, ал
болады, ал
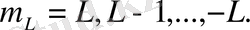
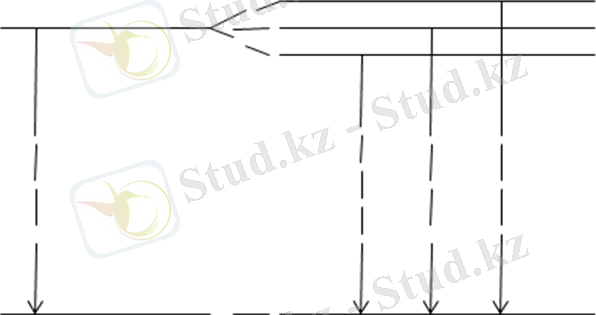
1. 3-суретте
 және
және
 күйлері арасындағы көшу (
күйлері арасындағы көшу (
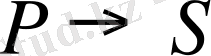 көшу) үшін деңгейлердің және спектрлік сызықтардың жіктелуі көрсетілген. Магнит өрісі жоқта жиілігі
көшу) үшін деңгейлердің және спектрлік сызықтардың жіктелуі көрсетілген. Магнит өрісі жоқта жиілігі
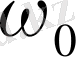 жалғыз сызық байқалады.
жалғыз сызық байқалады.

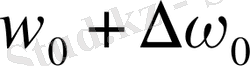
1. 4-сурет
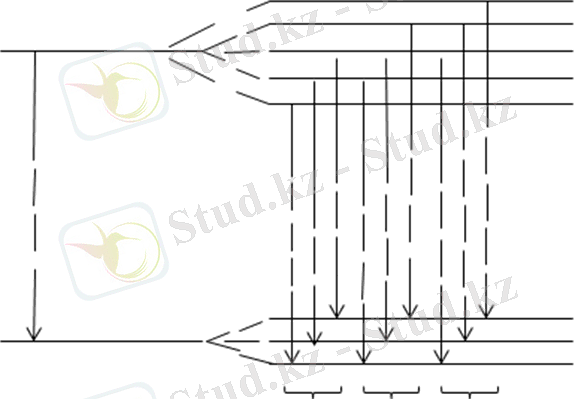 Өрісті қосқанда,
Өрісті қосқанда,
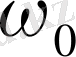 сызықтан басқа, бұған салыстырғанда симметриялы орналасқан жиіліктері
сызықтан басқа, бұған салыстырғанда симметриялы орналасқан жиіліктері
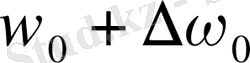 ,
,
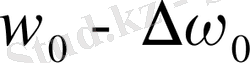 екі сызық пайда болады. Мысал ретінде гелий атомының
екі сызық пайда болады. Мысал ретінде гелий атомының
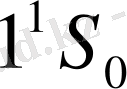 және
және
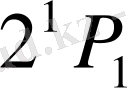 синглет энергетикалық деңгейлерін
синглет энергетикалық деңгейлерін
қарастырайық. Бұл деңгейлер арасында кванттық көшу ұлықсат етілген. Магнит өрісі жоқ кезде атом
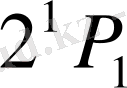 күйден
күйден
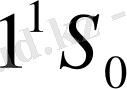 күйге көшкенде
күйге көшкенде
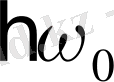 квант шығарылады; сонда толқын ұзындығы
квант шығарылады; сонда толқын ұзындығы
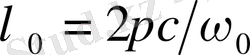 синглет спектрлік сызық шығарылады. Магнит өрісінде
синглет спектрлік сызық шығарылады. Магнит өрісінде
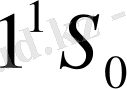 күйдегі атомның энергиясы өзгермейді. Өйткені,
күйдегі атомның энергиясы өзгермейді. Өйткені,
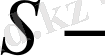 күй үшін
күй үшін
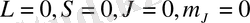 . Сонда (12) өрнегінен
. Сонда (12) өрнегінен
 болатындығы шығады, яғни
болатындығы шығады, яғни
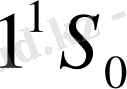 энергетикалық деңгейі магнит өрісінің әсеріне қарамастан, бұрынғыдай өзгеріссіз қалады. Керісінше,
энергетикалық деңгейі магнит өрісінің әсеріне қарамастан, бұрынғыдай өзгеріссіз қалады. Керісінше,
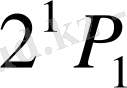 энергетикалық деңгейі магнит өрісінде жіктеледі. Өйткені,
энергетикалық деңгейі магнит өрісінде жіктеледі. Өйткені,
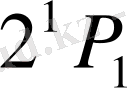 күйінде
күйінде
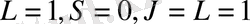 болатындықтан
болатындықтан
 магниттік кванттық саны үш мән қабылдайды
магниттік кванттық саны үш мән қабылдайды
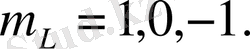
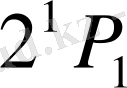 күйі үшін
күйі үшін
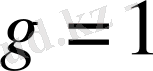 . Осыдан (12) өрнегіне сәйкес, энергиясы
. Осыдан (12) өрнегіне сәйкес, энергиясы

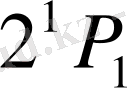 деңгейі магнит өрісінде энергиялары
деңгейі магнит өрісінде энергиялары
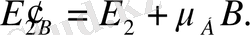

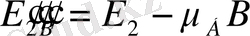 үш деңгейшеге жіктеледі.
үш деңгейшеге жіктеледі.
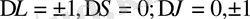 (13)
(13)
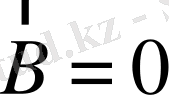 сұрыптау ережелеріне сәйкес
сұрыптау ережелеріне сәйкес
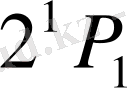

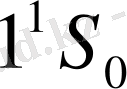 көшуі кезінде магнит өрісінде бір сызықтың орнына үш сызық шығарылады. Кванттық механикаға сәйкес
көшуі кезінде магнит өрісінде бір сызықтың орнына үш сызық шығарылады. Кванттық механикаға сәйкес
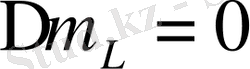 (
(
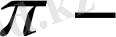 құраушы) үшін сызыққа сәйкес сәуле сызықтық поляризацияланған, өйткені электрлік вектор
құраушы) үшін сызыққа сәйкес сәуле сызықтық поляризацияланған, өйткені электрлік вектор
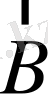 өріске параллель орналасқан.
өріске параллель орналасқан.
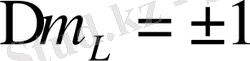 (
(
 құраушы) үшін сызықтарға сәйкес сәулелердің электрлік векторы магнит
құраушы) үшін сызықтарға сәйкес сәулелердің электрлік векторы магнит
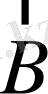 өріске перпендикуляр орналасқан; және бұл құраушылар дөңгелектік поляризацияланған (оң және сол дөңгелек бойынша) . Сәуле шығаратын диполь өріс бағытында бағдарланатындықтан
өріске перпендикуляр орналасқан; және бұл құраушылар дөңгелектік поляризацияланған (оң және сол дөңгелек бойынша) . Сәуле шығаратын диполь өріс бағытында бағдарланатындықтан
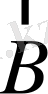 өріске параллель бағытта
өріске параллель бағытта
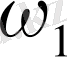 және
және
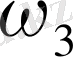 тек екі сызық шығарылады, бұлар үшін
тек екі сызық шығарылады, бұлар үшін
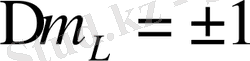 (диполь өз осі бағытында сәуле шығармайды) .
(диполь өз осі бағытында сәуле шығармайды) .
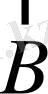 өріске перпендикуляр бағытта үш сызық шығарылады.
өріске перпендикуляр бағытта үш сызық шығарылады.
1. 4- суретте күрделірек жағдай,
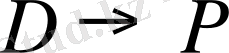 көшуі келтірілген. Бұл жағдайда бастапқы сызық магнит өрісінде тоғыз құраушыға жіктелетін сияқты болып көрінеді. Бірақ, шынында, жоғарыдағыдай тек үш сызық-жиілігі
көшуі келтірілген. Бұл жағдайда бастапқы сызық магнит өрісінде тоғыз құраушыға жіктелетін сияқты болып көрінеді. Бірақ, шынында, жоғарыдағыдай тек үш сызық-жиілігі
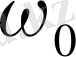 сызық, және бұған симметриялы орналасқан жиіліктері
сызық, және бұған симметриялы орналасқан жиіліктері
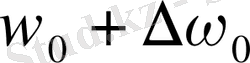 ,
,
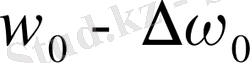 екі сызық-барлығы тек үш сызық алынады. Қарастырылған жағдайлардағы құраушылардың
екі сызық-барлығы тек үш сызық алынады. Қарастырылған жағдайлардағы құраушылардың
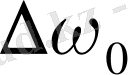 ығысуы қалыпты немесе лоренцтік ығысуы деп аталады.
ығысуы қалыпты немесе лоренцтік ығысуы деп аталады.
Зееманның күрделі құбылысы.
Нәзік түзілісі бар сызықтар магнит өрісінде үштен көп құраушыға жіктеледі; ал
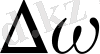 жіктелу шамасы
жіктелу шамасы
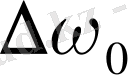 қалыпты ығысудың рационалдық бөлшегі:
қалыпты ығысудың рационалдық бөлшегі:
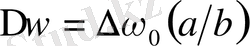
болып келеді; мұндағы
 және
және
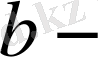 кішкентай бүтін сандар. Спектрлік сызықтардың осындай жіктелуі Зееманның күрделі немесе аномаль құбылысы деп аталады.
кішкентай бүтін сандар. Спектрлік сызықтардың осындай жіктелуі Зееманның күрделі немесе аномаль құбылысы деп аталады.
Зееманның күрделі құбылысы деңгейлердің
 жіктелу шамасының Ланде көбейткішіне тәуелді болуымен түсіндіріледі, яғни түптеп келгенде, электрон спиннің болуы және спиннің екі еселі магнетизмімен түсіндіріледі.
жіктелу шамасының Ланде көбейткішіне тәуелді болуымен түсіндіріледі, яғни түптеп келгенде, электрон спиннің болуы және спиннің екі еселі магнетизмімен түсіндіріледі.
 және
және
 көшулерінен тұратын натрий дублетінің жіктелуін қарастырайық. 1. 5-суретте деңгейлердің жіктелуі және
көшулерінен тұратын натрий дублетінің жіктелуін қарастырайық. 1. 5-суретте деңгейлердің жіктелуі және
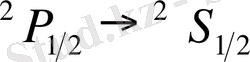 ,
,
 сызықтары үшін
сызықтары үшін
 сұрыптау ережесі ұлықсат ететін көшулер көрсетілген.
сұрыптау ережесі ұлықсат ететін көшулер көрсетілген.
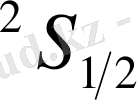 деңгейі
деңгейі
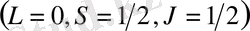 үшін энергияның магнит өрісі әсерінен өсімшесі
үшін энергияның магнит өрісі әсерінен өсімшесі
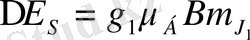 болады, мұнда
болады, мұнда
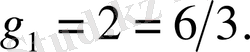
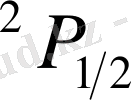 деңгейі
деңгейі
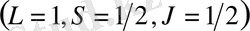 үшін
үшін
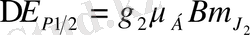 мұнда
мұнда
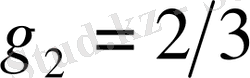 .
.
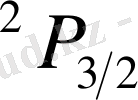 деңгейі
деңгейі
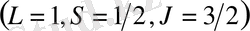 үшін
үшін
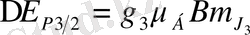 мұнда
мұнда
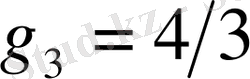 .
.
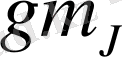
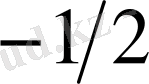
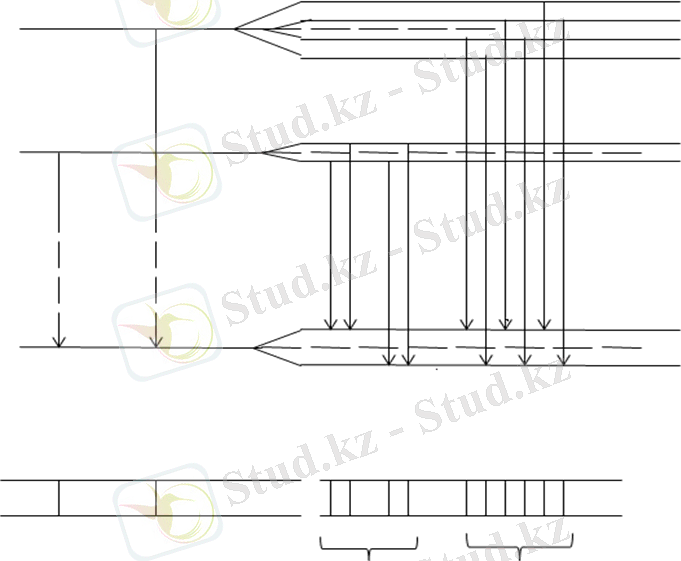

1. 5-сурет
Магнит өрісі жоқ кездегі бастапқы сызыққа салыстырғанда магнит өрісінде сызықтардың ығысуы мына өрнекпен анықталады:
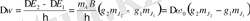 (14)
(14)
 сызығы үшін 1. 5-суреттегі деңгейлер арасындағы көшулерді кескіндейтін түзулер бойынша үзілісінде тиісті сызықтар үшін
сызығы үшін 1. 5-суреттегі деңгейлер арасындағы көшулерді кескіндейтін түзулер бойынша үзілісінде тиісті сызықтар үшін
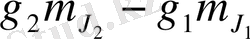 айырмасын анықтауға болады. Суреттен өріс қосылғанда бастапқы сызықтың тіпті болмайтындығын көруге болады. Оның орнына төрт сызық пайда болады, бұлардың
айырмасын анықтауға болады. Суреттен өріс қосылғанда бастапқы сызықтың тіпті болмайтындығын көруге болады. Оның орнына төрт сызық пайда болады, бұлардың
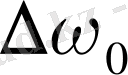 лоренцтік қалыпты ығысу бірлігіндегі ығысуы
лоренцтік қалыпты ығысу бірлігіндегі ығысуы
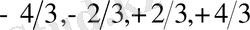 болады. Мұны мына түрде жазуға болады:
болады. Мұны мына түрде жазуға болады:
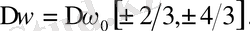
Ал
 сызығы үшін өріс қосылғанда пайда болатын алты сызықтың ығысулары мынаған тең:
сызығы үшін өріс қосылғанда пайда болатын алты сызықтың ығысулары мынаған тең:
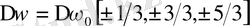
Пашен-Бак эффекті
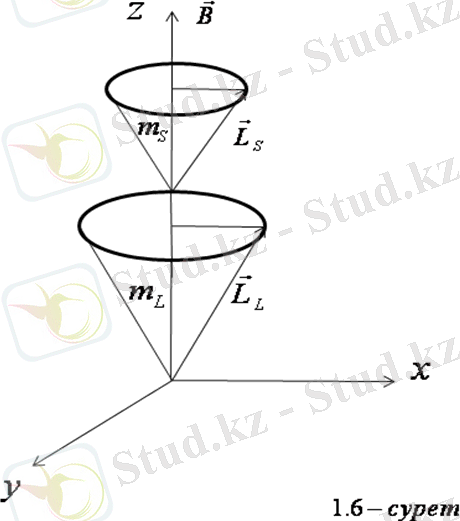 1912 ж. Пашен және Бак өте күшті магнит өрістерінде құраушылары жақын орналасқан мультиплеттердің зеемандық жіктелуінің күрделі көрінісі қарапайым көрініске ауысатынын байқаған. Сонда Зееманның күрделі құбылысы қарапайым құбылысқа айналатындай, мультиплет сызық күшті өрістерде өзін қарапайым синглет сызық сияқты байқатады. Осы құбылыс Пашен-Бак құбылысы деп аталады. Осы құбылысты жартылай классикалық әдіс-атомның векторлық моделі негізінде түсіндіреміз. Егер деңгейлердің магнит өрісіндегі
1912 ж. Пашен және Бак өте күшті магнит өрістерінде құраушылары жақын орналасқан мультиплеттердің зеемандық жіктелуінің күрделі көрінісі қарапайым көрініске ауысатынын байқаған. Сонда Зееманның күрделі құбылысы қарапайым құбылысқа айналатындай, мультиплет сызық күшті өрістерде өзін қарапайым синглет сызық сияқты байқатады. Осы құбылыс Пашен-Бак құбылысы деп аталады. Осы құбылысты жартылай классикалық әдіс-атомның векторлық моделі негізінде түсіндіреміз. Егер деңгейлердің магнит өрісіндегі
 жіктелуі шамасы бойынша табиғи мультиплеттік
жіктелуі шамасы бойынша табиғи мультиплеттік
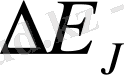 жіктелуден едәуір артық, яғни
жіктелуден едәуір артық, яғни
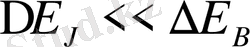 болса, онда мұндай магнит өрісі күшті деп есептеледі.
болса, онда мұндай магнит өрісі күшті деп есептеледі.
Күшті магнит өрісінде
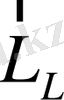 және
және
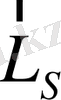 арасындағы байланыс үзіледі де, осындай өрісте векторлардың әрқайсысы бірінші жуықтауда бірінен-бірі өздерін тәуелсіз сияқты көрсетеді; бұлар
арасындағы байланыс үзіледі де, осындай өрісте векторлардың әрқайсысы бірінші жуықтауда бірінен-бірі өздерін тәуелсіз сияқты көрсетеді; бұлар
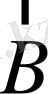 магнит өрісі бағытын айнала тәуелсіз прецессияланады. Енді
магнит өрісі бағытын айнала тәуелсіз прецессияланады. Енді
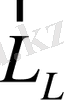 және
және
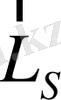 векторлары өріс бағытына бір-бірінен тәуелсіз бағдарланады. (1. 6-сурет) . Осыдан атомның
векторлары өріс бағытына бір-бірінен тәуелсіз бағдарланады. (1. 6-сурет) . Осыдан атомның
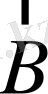 өріспен
өріспен
 әсерлесу энергиясы
әсерлесу энергиясы
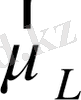 орбиталық магниттік момент пен
орбиталық магниттік момент пен
 спиндік магниттік моменттің жеке-жеке
спиндік магниттік моменттің жеке-жеке
 өріспен әсерлесу энергияларының қосындысы арқылы анықталатын болады.
өріспен әсерлесу энергияларының қосындысы арқылы анықталатын болады.
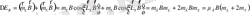
Атомның
 магнит өрісіндегі энергиясы мынаған тең:
магнит өрісіндегі энергиясы мынаған тең:
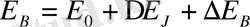 (15)
(15)
мұндағы
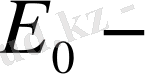 атомның спин-орбиталық әсерлесу ескерілмегендегі энергиясы;
атомның спин-орбиталық әсерлесу ескерілмегендегі энергиясы;
 спин-орбиталық әсерлесу энергиясы;
спин-орбиталық әсерлесу энергиясы;
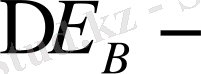 атомның сыртқы магнит өрісімен әсерлесу энергиясы.
атомның сыртқы магнит өрісімен әсерлесу энергиясы.
Спин-орбиталық әсерлесу энергиясы былай анықталады:
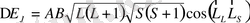 (16)
(16)
Күшті магнит өрісінде
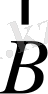 бағытын айнала
бағытын айнала
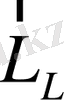 және
және
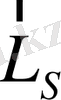 векторлары тәуелсіз , бұлардың арасындағы бұрыш үздіксіз өзгереді. Сондықтан (16) өрнегіндегі
векторлары тәуелсіз , бұлардың арасындағы бұрыш үздіксіз өзгереді. Сондықтан (16) өрнегіндегі
 үшін оның уақыт бойынша орташа мәнін алу керек; ол былай анықталады:
үшін оның уақыт бойынша орташа мәнін алу керек; ол былай анықталады:
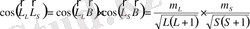 (17)
(17)
(17), (16), (14) өрнектерін (15) өрнегіне қоямыз, сонда
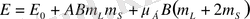 (18)
(18)
Сонымен, күшті магнит өрістерінде атомның екі деңгейі энергияларының айырмасы мынаған тең:
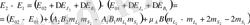
немесе
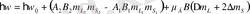 (19)
(19)
Сұрыптау ережелеріне сәйкес
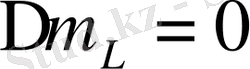 (
(
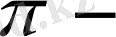 құраушы)
құраушы)
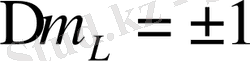 (
(
 құраушы)
құраушы)
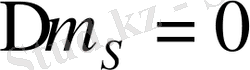 болатын көшулері ғана болуы мүмкін. Демек,
болатын көшулері ғана болуы мүмкін. Демек,
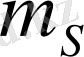 -тері бірдей деңгейлер арасында ғана көшулер болуы мүмкін, яғни көшулер кезінде
-тері бірдей деңгейлер арасында ғана көшулер болуы мүмкін, яғни көшулер кезінде
 шарты орындалуға тиіс.
шарты орындалуға тиіс.
Сұрыптау ережелерін ескеріп, күшті магнит өрісінде атом мына жиіліктерді шығарады деген қорытындыға келеміз:
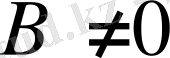
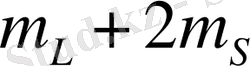

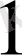

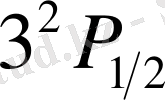



1. 7-сурет
(20)
Сонымен, күшті магнит өрісінде мультиплет орталығынан есептегенде
 шамасына ығысқан
шамасына ығысқан
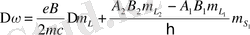 (21)
(21)
құраушылар пайда болады.
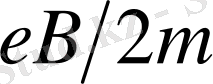 қарапайым зеемандық жіктелу шамасына тең болғандықтан, (21) өрнектегі бірінші қосылғыш сызықтың
қарапайым зеемандық жіктелу шамасына тең болғандықтан, (21) өрнектегі бірінші қосылғыш сызықтың
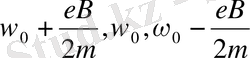
қарапайым зеемандық үш құраушыға жіктелуін береді. Ал осы құраушының әрқайсысы (21) өрнектегі екінші қосылғыштың әсерінен
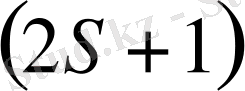 құраушыға жіктелетін болады. Бұлардың ара қашықтығы сызықтың табиғи мультиплеттік жіктелу енімен шамалас және ол сыртқы магнит өрісінің
құраушыға жіктелетін болады. Бұлардың ара қашықтығы сызықтың табиғи мультиплеттік жіктелу енімен шамалас және ол сыртқы магнит өрісінің
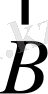 индукциясына тәуелсіз.
индукциясына тәуелсіз.
Пашен-Бак құбылысындағы құраушылардың нәзік түзілісінің алғашында байқалмауы, ал тұтас көрінісі қарапайым Зееман құбылысы сияқты қабылдануы осыдан.
... жалғасыШтарк эффекті
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz