Дифференциалдық теңдеулер курсында тірек конспектілерді пайдалану және теңдеулерді шешу әдістері


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 36 бет
Таңдаулыға:
МАЗМҰНЫ
КІРІСПЕ . . . 3
I тарау . 1. 1. Дифференциалдық теңдеулер. Негізгі ұғымдар . . . 4
1. 2. Айнымалылары ажыратылатын теңдеулер . . . 10
1. 3. Біртекті және оларға келтірілетін теңдеулер . . . 15
II тарау. 2. 1. Сызықты теңдеулер . . . 19
2. 2. Бернулли теңдеуі . . . 24
2. 3. Толық дифференциалдық теңдеулер . . . 26
2. 4. Интегралдық көбейткіш . . . 28
2. 5. Жоғарғы ретті дифференциалдық теңдеулер. Ретін төмендету әдісі . . . 31
2. 6. n-ретті сызықтық дифференциалдық теңдеулер . . . 33
Қорытынды . . . 36
Пайдаланылған әдебиеттер . . . 37
КІРІСПЕ
Ғылыми-техникалық прогресс пен өндірістік технологияның дамуы, экономиканың өркендеу дәуірінде қоғамға жан-жақты дамыған, белсенді өз бетінше жасампаздықпен ойлай білетін жастардың тұрақты легінің келіп отыруын талап етеді. Сондықтан оқыту процессі деңгейін арттыру арқылы, ақыл-ойы жетілген, жан-жақты дамыған, жасампаздықпен еңбек етуге қабілетті, өз тағдырларын өздері шеше алатын, өз бетінше білімін толықтыру және өздігінен кәсіби шеберлігін арттыру мүмкіндігі бар азаматтар даярлап білім саласындағы басты мақсат болып табылады.
Ғылыми ақпараттар ағынының жедел қарқынмен өсуі, жалпы білім беретін студенттерді өз бетінше жаңа білімдер игеруге қабілетті етіп тәрбиелеу мен оқытуды талап етеді.
Өз бетінше білім алу үшін студент өз танымдық қызметі нысанның мәнін ұғынып, оның іс әрекет жолдарын игеруге тура келеді. Сол себепті студенттерді жаңа білімдерді алу “технологиясын” дифференциалдық теңдеулер курсында тірек конспектілерін қолдану жолдарын мақсатты түрде оқыту қажеттігі туындайды.
Бұл дипломдық жұмысымда дифференциалдық теңдеулер курсында тірек конспектілерін қолдану, және де дифференциалдық теңдеулерді шешу жолдарын қарастырамын. Дипломдық жұмыс II тараудан тұрады.
§ 1. 1. Дифференциялдық теңдеулер. Негізгі ұғымдар .
§ 1. 2. Айнымалылары ажыратылатын теңдеулердің шешімі көрсетіледі.
§ 1. 3. Біртекті және оларға келтірілетін теңдеулер, f(x, y) функциясы өзінің аргументтеріне қарай нолінші дәрежелі функция болса, онда мұндай теңдеуді біртекті деп атайды, және теңдеулердің шешімдерінің айқын формулалары алынады.
II тарауда §2. 1. Сызықты теңдеулер, теңдеулердің анықтамасы, теңдеудің жалпы шешімінің формуласын көрсетеміз.
§ 2. 2. Бернулли теңдеуінің шешімін, қайсыбір жағдайларда Бернулли теңдеуін y-u(x) ·v(x) алмастыруын қолданып шешкен ыңғайлы екендігі көрсетіледі.
§ 2. 3. Толық дифференциалдық теңдеулер оны жалпы шешімін табу қарастырылады.
§ 2. 4. Интегралдық көбейткіш, кез келген теңдеу толық дифференциалды болмайды. Демек,
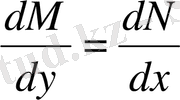 шарт әр уақытта орындалмайды екен. Осыған байланысты берілген теңдеуді қайсыбір
шарт әр уақытта орындалмайды екен. Осыған байланысты берілген теңдеуді қайсыбір
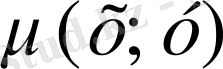
функциясына көбейтіп толық дифференциалды теңдеу алуға болатындығы қарстырылады.
§ 2. 5-те Жоғарғы ретті дифференциалдық теңдеулер. Ретін төмендету әдісі көрсетіледі.
§ 2. 6-да n-ретті сызықтық дифференциалдық теңдеулер қарастырылып, жалпы шешім табу қарастырылады. Диплом жұмысының артында қорытынды, әдебиеттер тізімі көрсетіледі
І-тарау.
ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР
1. 1. Дифференциялдық теңдеулер. Негізгі ұғымдар.
Дифференциалдық теңдеулер деп тәуелсіз айнымалыны
х
пен ізделінетін
у=у(х)
функциясын және оның
у'(х), у''(х), . . . ,
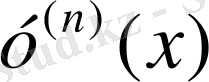 туындыларын байланыстыратын теңдеуді атайды. Оны жалпы жағдайда
туындыларын байланыстыратын теңдеуді атайды. Оны жалпы жағдайда
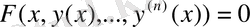 (1)
(1)
түрде жазуға болады. Басқаша айтқанда ізделінетін функцияның туындысы немесе дифференциалы кіретін теңдеуді атайды.
Ізделінетін функция тек бір аргументтен тәуелді болса, теңдеуді жай дифференциалдық теңдеу немесе дифференциалдық теңдеу деп атайды.
Бірнеше аргументтен ізделінетін функцияны және оның дербес туындыларын қамтитын теңдеуді дербес туындылы дифференциалдық теңдеу деп атайды.
Алдағы уақытта тек жай дифференциалдық теңдеулерді қарастырамыз. Теңдеуге кіретін туындының ең жоғарғы ретін дифференциалдық теңдеудің реті деп атайды. Мысалы, (1) теңдеу n-ретті дифференциалдық теңдеу. Егер (1) теңдеуде n=1 болса, онда 1- ретті теңдеудің
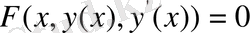
жалпы түрін аламыз.
Егер бұл теңдеуді у' туындысына қарай шешу мүмкін болса, онда
у'=f(x, y) (2)
(2) теңдеу туындысына қарай шешілген деп атайды. Егер (1) теңдеуде
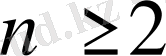 болса, онда оны жоғарғы ретті дифференциалдық теңдеу деп атайды.
болса, онда оны жоғарғы ретті дифференциалдық теңдеу деп атайды.
Дифференциалдық теңдеудің шешімі қайсыбір
(a, b)
интервалында анықталған, реті дифференциалдық теңдеудің ретіндей болатын туындылары үзіліссіз және
х
бойынша (
х
 (a, b) ) теңдеуді тепе-теңдікке айналдыратын
(a, b) ) теңдеуді тепе-теңдікке айналдыратын
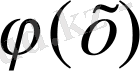 функциясын айтады.
функциясын айтады.
Мысалы, егер
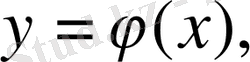
 функциясы (1) теңдеудің шешімі болса, онда
функциясы (1) теңдеудің шешімі болса, онда
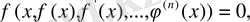

Қайсыбір жағдайда теңдеу шешімі айқындалмаған түрде алынады
Дифференциалдық теңдеу шешімінің графигін осы теңдеудің интегралдық қисығы деп атайды.
Қысқаша интегралдық қисықты теңдеу шешімі деп те айтады.
1-мысал.
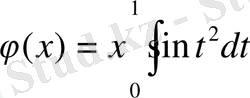 функциясының
функциясының
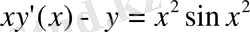
дифференциалдық теңдеудің шешімі болатынын көрсету керек.
Шешуі.
 функциясының туындысын табамыз
функциясының туындысын табамыз
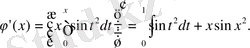
Енді
 пен
пен
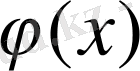 өрнектерін берілген теңдеуге қоямыз:
өрнектерін берілген теңдеуге қоямыз:
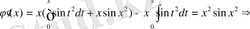
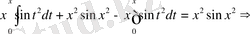
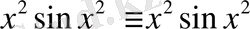
Демек,
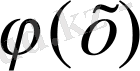 функциясы берілген теңдеудің шешімі екен. Берілген дифференциалдық теңдеудің шешімін табу процесін интегралдау деп атайды. Егер барлық шешімдерді элементар функциялар арқылы табу мүмкін болса, онда теңдеу элементар функциялар арқылы интегралданады деп аталады. Егер де теңдеу шешімі элемантар функциялар арқылы алынбаса, бірақ оның шешімі элемантар функциялардан алынған анықталмаған интеграл түрінде болса, онда теңдеу квадратурада шешілген деп айтады. Квадратурада деп анықталмаған интеграл алу процесін айтады. Егер теңдеу шешімі элемантар функциялар арқылы немесе квадратурада алынса, онда дифференциалдық теңдеу шекті түрде интегралданады деп айтады. Алдағы уақытта тек осындай теңдеулерді қарастырамыз.
функциясы берілген теңдеудің шешімі екен. Берілген дифференциалдық теңдеудің шешімін табу процесін интегралдау деп атайды. Егер барлық шешімдерді элементар функциялар арқылы табу мүмкін болса, онда теңдеу элементар функциялар арқылы интегралданады деп аталады. Егер де теңдеу шешімі элемантар функциялар арқылы алынбаса, бірақ оның шешімі элемантар функциялардан алынған анықталмаған интеграл түрінде болса, онда теңдеу квадратурада шешілген деп айтады. Квадратурада деп анықталмаған интеграл алу процесін айтады. Егер теңдеу шешімі элемантар функциялар арқылы немесе квадратурада алынса, онда дифференциалдық теңдеу шекті түрде интегралданады деп айтады. Алдағы уақытта тек осындай теңдеулерді қарастырамыз.
Егер (1) теңдеу жоғарғы ретті туындыға қарай шешілсе:
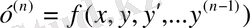 (3)
(3)
онда теңдеу нормалды түрде берілген деп атайды. (2) теңдеу 1-ретті дифференциалдық теңдеудің нормалды түрі болады.
Егер (3) теңдеудің оң жағындағы өрнек белгісіз функция мен оның туындылары бойынша сызықты және олардың көбейтінділерін қамтыса онда мұндай теңдеулерді сызықты дифференциалдық теңдеулер деп атайды.
(2) дифференциалдық теңдеудің дербес жағдайын қарастырамыз
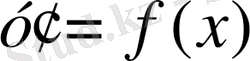 (4)
(4)
Интегралдық есептеуден белгілі
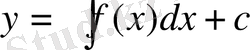 (5)
(5)
мұндағы с кез келген тұрақты сан, сонымен қатар тұрақты с -ның әр түрлі мәндеріндегі функциялары да (4) теңдеудің шешімдері болады.
Сонымен, (4) теңдеудің (5) түріндегі шешімінде бір тұрақты сан (параметр) бар:
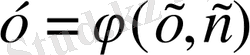
мұндай шешімді 1-ретті дифференциалдық теңдеудің жалпы шешімі деп атайды. Жалпы шешімінен параметрдің бір белгілі мәніне сәйкес келетін шешімнің мәнін теңдеудің дербес (дара) шешімі деп атайды. Жалпы шешімнен дербес шешімді табу үшін әдетте белгісіз функцияның қайсыбір
 нүктесіндегі мәні беріледі. Бұл
нүктесіндегі мәні беріледі. Бұл
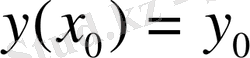 шартын бастапқы шарт деп атайды. (2) теңдеудің
шартын бастапқы шарт деп атайды. (2) теңдеудің
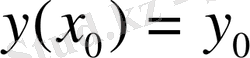 шартты қанағаттандыратын шешімін табу есебін Коши есебі деп атайды.
шартты қанағаттандыратын шешімін табу есебін Коши есебі деп атайды.
(3) теңдеудің жалпы шешімі деп
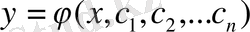 (6)
(6)
функциясын атайды. Бұдан n-ретті дифференциалдық теңдеудің жалпы шешіміне n тұрақты сан барын көреміз және осыдан қайсыбір дербес шешімді табу үшін төмендегі
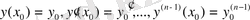 (7)
(7)
Егер жалпы шешім айқындалмаған түрде
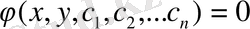
берілсе, онда оны (3) теңдеудің жалпы интегралы деп атайды.
Егер (2) теңдеуді
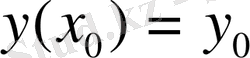 шартпен қарастырып, бұл теңдеудің шешімі бар ма, егер бар болса ол шешімі тек біреу ғана бола ма деген сұрауларға жауап іздейміз. Бұл сұраққа жауапты төмендегі шешімнің бар және оның жалғыз болуы туралы теорема береді.
шартпен қарастырып, бұл теңдеудің шешімі бар ма, егер бар болса ол шешімі тек біреу ғана бола ма деген сұрауларға жауап іздейміз. Бұл сұраққа жауапты төмендегі шешімнің бар және оның жалғыз болуы туралы теорема береді.
Теорема
. Егер (2) теңдеудің оң жағындағы функция тұйық
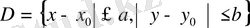 (a, b- қайсыбір сандар) облысында үзіліссіз және осы облыста
У
бойынша Липшиц шартын қанағаттандырса:
(a, b- қайсыбір сандар) облысында үзіліссіз және осы облыста
У
бойынша Липшиц шартын қанағаттандырса:
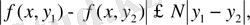
мұндағы N- тұрақты сан, онда берілген теңдеудің
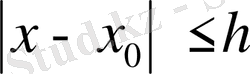
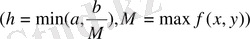 аралығында анықталған,
аралығында анықталған,
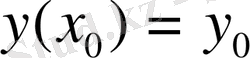 бастапқы шартын қанағаттандыратын тек жалғыз шешімі бар.
бастапқы шартын қанағаттандыратын тек жалғыз шешімі бар.
Ескерту
. Бұл теоремадағы Липшиц шартын D облысында
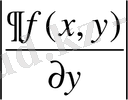 дербес туындының шектелген болу шартымен ауыстыруға болады.
дербес туындының шектелген болу шартымен ауыстыруға болады.
Бірінші ретті дифференциалдық теңдеудің ерекше шешімі (ерекше интегралдық қисығы) деп кез келген нүктеде Коши есебінің шешімі жалғыз болу шарты орындалмайтын шешімін атайды. Ерекше шешімді жалпы шешімді жалпы шешімнен кез келген тұрақты сан қайсыбір мәнінде алу мүмкін емес (бірақ оны с=с(х) ) болғанда алу мүмкін.
2-мысал. Дифференциалдық теңдеуді шешіңіз
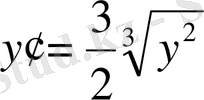
Шешуі. Мұнда
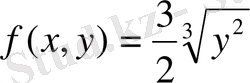 және ол
хОу
жазықтығының барлық нүктелерінде анықталған, үзіліссіз функция. Дербес туындысын табамыз:
және ол
хОу
жазықтығының барлық нүктелерінде анықталған, үзіліссіз функция. Дербес туындысын табамыз:
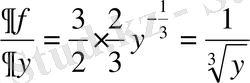
у=0 болғанда бұл туынды шексіздікке айналады. Сондықтан у=0 болғанда жоғарыдағы теореманың шарты орындалмайды. Олай болса Ох өсінің барлық нүктелерінде шешімнің жалғыз болмауы мүмкін. Берілген теңдеуді шешеміз:
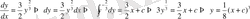
Сонымен берілген теңдеудің жалпы шешімі
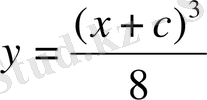 .
.
Сонымен қатар у=0 теңдеудің шешімі болатыны көрініп тұр. Демек,
Ох
өсінің әрбір нүктесі арқылы жоқ дегенде екі интегралдық қисық өтеді. Берілген теңдеудің интегралдық қисығы
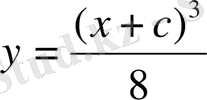 кубтық параболаның бөліктерінен тұратын сызықтар және
Ох
өсінің кесінділері болады. Мысалы,
кубтық параболаның бөліктерінен тұратын сызықтар және
Ох
өсінің кесінділері болады. Мысалы,
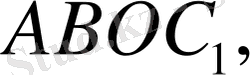
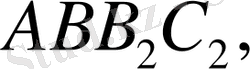
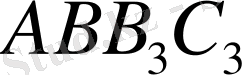 және т. с. с., бұдан
Ох
өсінің әрбір нүктесі арқылы интегралдық қисықтың шексіз жиыны өтетінін көреміз.
және т. с. с., бұдан
Ох
өсінің әрбір нүктесі арқылы интегралдық қисықтың шексіз жиыны өтетінін көреміз.
Берілген қисықтар тобы бойынша дифференциалдық теңдеуді құруға тоқталамыз.
Кез келген
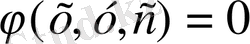 , (8) қисықтар тобы үшін, мұндағы
с
-параметр,
, (8) қисықтар тобы үшін, мұндағы
с
-параметр,
 - функциясының үзіліссіз дербес туындылары бар, дифференциалдық теңдеу құруға болатынын көреміз.
- функциясының үзіліссіз дербес туындылары бар, дифференциалдық теңдеу құруға болатынын көреміз.
(8) теңдеу у -ке қарай шешіледі деп жоримыз: у=у(х, с)
у -тің осы мәнін (8) теңдеуге апарып қоямыз
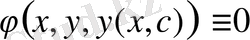
Бұл тепе-теңдікті х бойынша дифференциалдап:
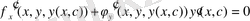
Төмендегі жүйені аламыз:
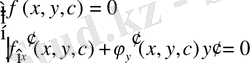 (9)
(9)
Бұл жүйедегі теңдеудің біреуінен
с
-ны тауып екіншісіне апарып қойсақ параметр
с
жойылады да
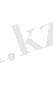 F(x, y, y’) =0 түрдегі дифференциалдық теңдеуді аламыз. Бұл теңдеуді (8) қисықтар тобының дифференциалдық теңдеуі деп атайды.
F(x, y, y’) =0 түрдегі дифференциалдық теңдеуді аламыз. Бұл теңдеуді (8) қисықтар тобының дифференциалдық теңдеуі деп атайды.
4-мысал.
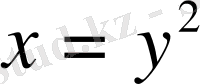 параболасының төбесін
параболасының төбесін
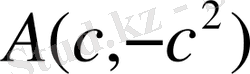 нүктесіне паралель жылжыту арқылы алынған қисықтар тобының теңдеуін құрамыз. Бұл топтардың дифференциалдық теңдеуін тауып, одан
нүктесіне паралель жылжыту арқылы алынған қисықтар тобының теңдеуін құрамыз. Бұл топтардың дифференциалдық теңдеуін тауып, одан
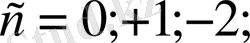 мәндеріне сәйкес келетін интегралдық қисықтарды бөлу керек.
мәндеріне сәйкес келетін интегралдық қисықтарды бөлу керек.
Шешуі: Параллель түрлендіруді жасау үшін
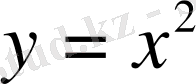 теңдеуіндегі
х
абциссасын
х-с
- ге, ал ордината
у
-ті
теңдеуіндегі
х
абциссасын
х-с
- ге, ал ордината
у
-ті
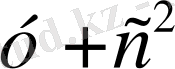 алмастыру керек. Нәтижесінде іздеп отырған параболалар тобын аламыз
алмастыру керек. Нәтижесінде іздеп отырған параболалар тобын аламыз
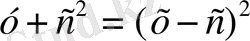 немесе
немесе
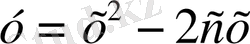 (10)
(10)
Бұл теңдеуде бір параметр с бар, сондықтан оны бірінші ретті дифференциалдық теңдеудің жалпы шешімі ретінде қарастыруға болады.
Дифференциалдық теңдеуді табу үшін (10) теңдеудің екі жағын х бойынша дифференциалдап (9) жүйені қараймыз:
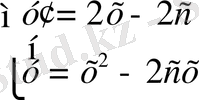
Екінші теңдеуден с -ны тауып, оны бірінші теңдеуге қойсақ
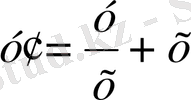 (11)
(11)
(10) топтағы әрбір қисық (11) теңдеудің интегралдық қисығы болатындығын байқаймыз. Сондықтан (10) теңдеудегі
с
-ның орнына берілген мәндерді қойып тиісті интегралдық қисықтар теңдеуін аламыз.
С=0
болса
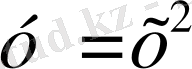 , с=1 болса
, с=1 болса
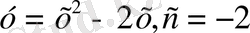 болғанда
болғанда
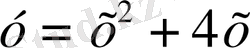 болады.
болады.
5-мысал.
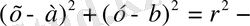 шеңберлер тобының дифференциалдық теңдеуін құру керек.
шеңберлер тобының дифференциалдық теңдеуін құру керек.
Шешуі. Қисықтар тобында a, b, r үш параметр бар.
Сондықтан берілген теңдеуді х бойынша үш рет дифференциалдаймыз:
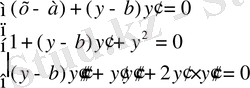
Немесе
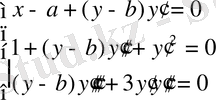
Бұдан a мен r параметрлері дифференциалдау процесінде жойылғанын байқаймыз. Екінші теңдеуден b -ні табамыз:
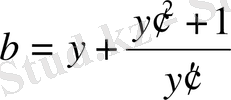
Мұны үшінші теңдеуге қойсақ:
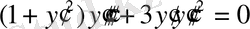 түріндегі дифференциалдық теңдеу шығады.
түріндегі дифференциалдық теңдеу шығады.
Енді (2) дифференциалдық теңдеудің геометриялық мағынасын қарастырамыз. Айталық
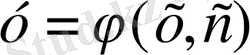 осы теңдеудің жалпы шешімі болсын. Бұл шешім
Оху
жазықтығында интегралдық қисықтар тобын анықтайды. (2) теңдеу әрбір
М(х, у)
нүктеде туынды мәнін анықтайды, демек осы нүкте арқылы өтетін интегралдық қисыққа жүргізілген жанаманың бұрыштық коэффициентін анықтайды. Сонымен, (2) дифференциалдық теңдеу бағыттар жиынын береді, немесе, әдетте, бағыттар өрісін анықтайды деп атайды.
осы теңдеудің жалпы шешімі болсын. Бұл шешім
Оху
жазықтығында интегралдық қисықтар тобын анықтайды. (2) теңдеу әрбір
М(х, у)
нүктеде туынды мәнін анықтайды, демек осы нүкте арқылы өтетін интегралдық қисыққа жүргізілген жанаманың бұрыштық коэффициентін анықтайды. Сонымен, (2) дифференциалдық теңдеу бағыттар жиынын береді, немесе, әдетте, бағыттар өрісін анықтайды деп атайды.
Демек, дифференциалдық теңдеуді интегралдау есебі геометриялық тұрғыдан қарағанда жанама бағыты сол нүктеге сәйкес келетін өріс бағытымен дәл келетіндей қисықтарды табуда екен.
(2) дифференциалдық теңдеу үшін
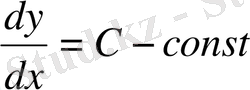 қатыс орындалатын геометриялық нүктелер орнын берілген теңдеудің изоклині деп атайды.
С
-ның әртүрлі мәндерінде изоклиндердің әртүрін аламыз.
С
-ға сәйкес келетін изоклин теңдеуі
қатыс орындалатын геометриялық нүктелер орнын берілген теңдеудің изоклині деп атайды.
С
-ның әртүрлі мәндерінде изоклиндердің әртүрін аламыз.
С
-ға сәйкес келетін изоклин теңдеуі
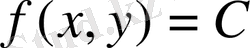 болады. Изоклин топтарын құрып, жуықтап интегралдық қисықтар тобын құруға болады. Берілген изоклинді қиып өтетін барлық интегралдық қисықтар абцисса осімен бірдей бұрыштар жасайды.
болады. Изоклин топтарын құрып, жуықтап интегралдық қисықтар тобын құруға болады. Берілген изоклинді қиып өтетін барлық интегралдық қисықтар абцисса осімен бірдей бұрыштар жасайды.
6-мысал.
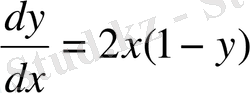 теңдеуінің интегралдық қисықтарын изоклиндердің көмегімен салыңыздар.
теңдеуінің интегралдық қисықтарын изоклиндердің көмегімен салыңыздар.
Шешуі. Берілген теңдеудің изоклиндері
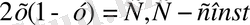 , теңдеуден анықталады.
с=0
болғанда,
2х(1-у) =0
болады да
х=0
және у=1 екі түзуін, сонымен қатар
, теңдеуден анықталады.
с=0
болғанда,
2х(1-у) =0
болады да
х=0
және у=1 екі түзуін, сонымен қатар
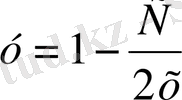 гиперболалар тобын береді. у=1 түзуі дифференциалдық теңдеудің шешімі болғандықтан интегралдық қисық болады. Ординаталар осімен интегралдық қисықтар тік бұрыш жасайды, демек олардың жанамасы абцисса осіне параллель болады. Бұл
х=0
қисығының нүктелері интегралдық қисықтар үшін кризистік нүктелер болатынын көрсетеді. Кризистік нүктелер характерін анықтау үшін
у=у(х)
функциясының екінші ретті туындысын табамыз.
гиперболалар тобын береді. у=1 түзуі дифференциалдық теңдеудің шешімі болғандықтан интегралдық қисық болады. Ординаталар осімен интегралдық қисықтар тік бұрыш жасайды, демек олардың жанамасы абцисса осіне параллель болады. Бұл
х=0
қисығының нүктелері интегралдық қисықтар үшін кризистік нүктелер болатынын көрсетеді. Кризистік нүктелер характерін анықтау үшін
у=у(х)
функциясының екінші ретті туындысын табамыз.
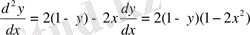
Демек, ординаталар осінің
у>1
болатындығы ординат осінің нүктелері интегралдық қисықтың минимум нүктелері болады. Сонымен қатар
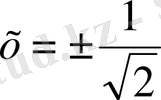 нүктелер интегралдық қисықтар тобының иілу нүктелері болады. Ары қарай,
х=0
және
у=1
түзулер координаталар жазықтығын әрқайсысында
нүктелер интегралдық қисықтар тобының иілу нүктелері болады. Ары қарай,
х=0
және
у=1
түзулер координаталар жазықтығын әрқайсысында
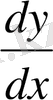 туындысының таңбасы бірдей болатын төрт бөлікке бөледі. Ендеше,
у>1
болғанда интегралдық қисықтар
х=0
түзуін қиып өтіп
у(х)
функциясының өсу облысынан оның кему облысына өтеді. Тағы да
с=1
және
с=-1
болғандағы екі изоклинді қарастырамыз:
туындысының таңбасы бірдей болатын төрт бөлікке бөледі. Ендеше,
у>1
болғанда интегралдық қисықтар
х=0
түзуін қиып өтіп
у(х)
функциясының өсу облысынан оның кему облысына өтеді. Тағы да
с=1
және
с=-1
болғандағы екі изоклинді қарастырамыз:
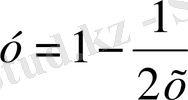 және
және
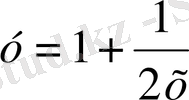
Осы изоклиндермен қиылысу нүктелеріндегі интегралдық қисықтарға жүргізілген жанамалар абцисса осімен сәйкес
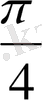 және
және
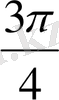 бұрыштар жасайды.
бұрыштар жасайды.
1. 2. Айнымалылары ажыратылатын теңдеулер
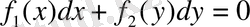 (1)
(1)
түріндегі теңдеуді қарастырамыз, мұндағы
dx-
тің алдындағы функция тек
х
-тен, ал
dy
-тің алдындағы функция тек
у
-тен тәуелді. Бұл жағдайда дифференциалдық теңдеудің айнымалылары бөлінген немесе ажыратылған деп атайды. Қарсатырып отырған
х
пен
у
мәндерінде
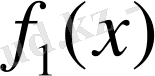 пен
пен
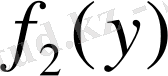 функциялары үзіліссіз деп жорысақ, онда (1) теңдеуді интегралдауға болады.
функциялары үзіліссіз деп жорысақ, онда (1) теңдеуді интегралдауға болады.
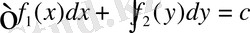 (2)
(2)
(2) қатыс тәуелсіз айнымалы х -ті, белгісіз у -ті және тұрақты С санының арасындағы байланысты береді, демек ол жалпы шешім болады.
Тәуелсіз айнымалы айқын түрде кірмейтін бір теңдеуді келтіреміз
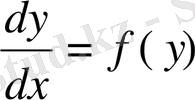
Бұл теңдеудің екі жағын да
dx-
ке көбейтіп, сонан соң
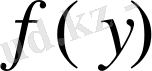 бөлеміз
бөлеміз
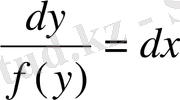 немесе
немесе
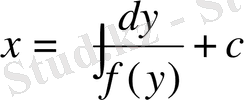 ,
,
Мұндағы х у -тен функция ретінде қарастырылады.
Нормальдық түрде берілген бірінші ретті дифференциалдық теңдеудегі туындыны дифференциалдар қатынасы арқылы жазамыз.
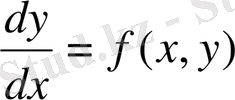 (3)
(3)
Егер (3) теңдеудің оң жағы біреуі тек х -тен тәуелді болатын екі функцияның көбейтіндісі түрінде жазылса, онда (3) теңдеуді айнымалылары ажыратылатын (бөлінетін) теңдеу деп атайды. Демек
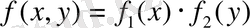
болады да (3) теңдеу былай жазылады:
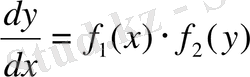
бұл теңдеудің екі жағын
dx
-ке көбейтіп
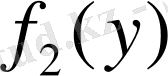 -ке бөлеміз:
-ке бөлеміз:
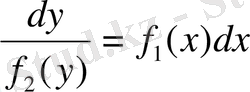 (4)
(4)
(4) теңдеудің айнымалылары ажыратылатын және дифференциалдар өзара тең, онда олардың анықталмаған интегралдары өзара тұрақты қосылғышпен айырмалатыны белгілі:
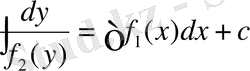 (5)
(5)
мұндағы с- тұрақты сан. (5) қатыс у -ті және тәуелсіз айнымалы х -ті байланыстырады, демек ол (3) теңдеудің жалпы шешімі болады. Егер теңдеу
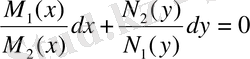
бұл айнымалылары бөлінген теңдеу.
Ендеше жалпы шешімі
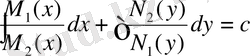 болады.
болады.
Ескертулер. 1. Теңдеуді
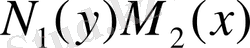 көбейтіндіге бөлгенде теңдеудің осы көбейтіні нольге айналдыратын дербес шешімі жоғалуы мүмкін.
көбейтіндіге бөлгенде теңдеудің осы көбейтіні нольге айналдыратын дербес шешімі жоғалуы мүмкін.
2.
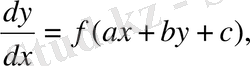 a, b, c-тұрақты сандар түрдегі дифференциалдық теңдеуді
z=ax+by+c
алмастыруы арқылы айнымалылары бөлінетін теңдеуге түрлендіруге болады.
a, b, c-тұрақты сандар түрдегі дифференциалдық теңдеуді
z=ax+by+c
алмастыруы арқылы айнымалылары бөлінетін теңдеуге түрлендіруге болады.
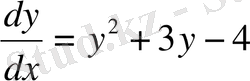 1-мысал.
1-мысал.
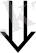
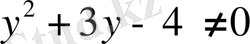
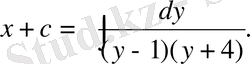

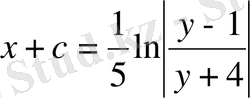

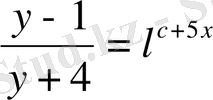
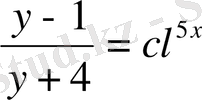
 ,
,
2-мысал. Төмендегі теңдеудің у(0) =1, бастапқы шартын қанағаттандыратын дербес шешімін табыңыз:
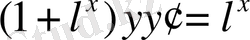 (7)
(7)
Шешуі. Берілген теңдеуді көшіріп жазамыз
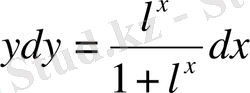 ; бұдан
; бұдан
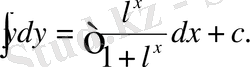
Оң жақтағы интеграл үшін
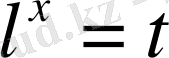 алмастыруын жасаймыз. Сонда
x=
ln
t,
алмастыруын жасаймыз. Сонда
x=
ln
t,
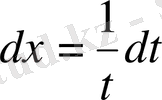 болады да
болады да
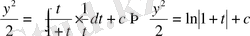 (8)
(8)
(8) өрнек (7) теңдеудің жалпы шешімі.
Енді дербес шешімді табу үшін (8) де х=0 және у=1 мәндерін қойып, тұрақты с тиісті мәнін табамыз
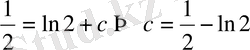
Сонда іздеп отырған дербес шешім
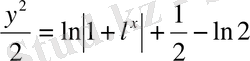
болады. Немесе бұдан
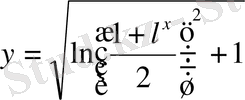
3-мысал. Дифференциалдық теңдеуді шешеміз:
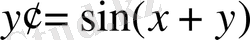 (9)
(9)
Шешуі. (9) теңдеу айнымалылары бөлінетін теңдеу емес, алайда
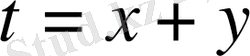 алмастыру арқылы сол түрге келтіруге болады. Туындысын табамыз:
алмастыру арқылы сол түрге келтіруге болады. Туындысын табамыз:
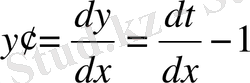 . Сонда (9) теңдеу былай жазылады
. Сонда (9) теңдеу былай жазылады
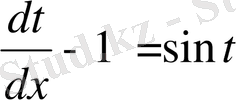
немесе
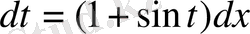 (10)
(10)
Айталық
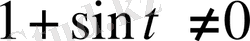 болсын, сонда (10) теңдеудің жалпы шешімі мына түрде жазылады:
болсын, сонда (10) теңдеудің жалпы шешімі мына түрде жазылады:
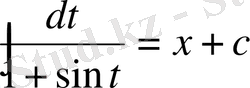
Сол жақтағы интегралды универсалдық алмастыру
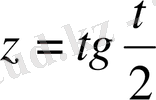 арқылы есептейміз.
арқылы есептейміз.
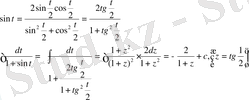
Сонымен (10) теңдеудің жалпы шешімі мына түрде жазылады:
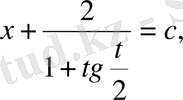 немесе
немесе
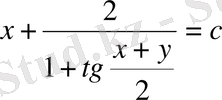
Айталық,
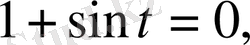 бұдан
бұдан
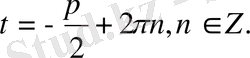 Олай болса
Олай болса
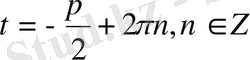 функциялары (10) теңдеудің шеімдері, ал
функциялары (10) теңдеудің шеімдері, ал
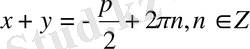 (9) теңдеудің шешімдері болады.
(9) теңдеудің шешімдері болады.
Айнымалылары ажыратылатын теңдеулерде тірек конспектілерін қолдану:
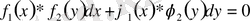

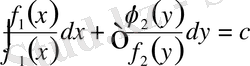
1-мысал:

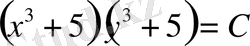

1. 3. Біртекті және оларға келтірілетін теңдеулер
Егер
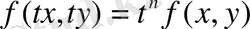 тепе-теңдігі орындалса, онда
тепе-теңдігі орындалса, онда
 функциясының аргументтері х пен у бойынша n дәрежелі (өлшемді) біртекті функция.
функциясының аргументтері х пен у бойынша n дәрежелі (өлшемді) біртекті функция.
Мысалы,
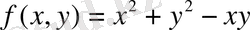 2-дәрежелі біртекті функция.
2-дәрежелі біртекті функция.
Шынында
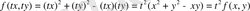
Егер
n=0
болса нөлінші дәрежелі біртекті функцияны аламыз. Мысалы,
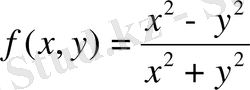 - нөлінші дәрежелі біртекті функция. Шынында
- нөлінші дәрежелі біртекті функция. Шынында
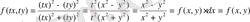
түріндегі дифференциалдық теңдеудің оң жағынжағы
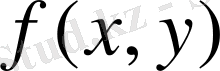 функциясы өзінің аргументтеріне қарай нөлінші дәрежелі функция болса, онда мұндай теңдеулерді біртекті деп атайды.
функциясы өзінің аргументтеріне қарай нөлінші дәрежелі функция болса, онда мұндай теңдеулерді біртекті деп атайды.
Біртекті теңдеуді әр уақытта мына түрде жазуға болады.
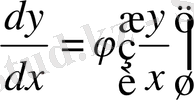 (1)
(1)
(1) теңдеуге
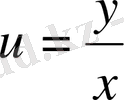 белгісіз функциясын енгізіп, айнымалыларды бөлінетін теңдеуге келтіреміз:
белгісіз функциясын енгізіп, айнымалыларды бөлінетін теңдеуге келтіреміз:
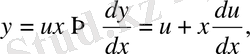
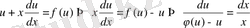
Бұдан
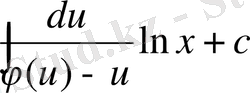 , енді
, енді
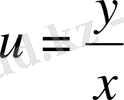 алмастырып берілген теңдеудің жалпы шешімін аламыз.
алмастырып берілген теңдеудің жалпы шешімін аламыз.
Ескерту. Біртекті теңдеулерді шешкенде, оларды (1) түрге келтіру міндетті емес, бірден у=ux алмастыруын жасауға болады.
1-мысал. . Дифференциалдық теңдеуді шешеміз:
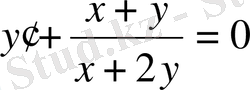 (2)
(2)
Шешуі. Бұл теңдеуді көшіріп жазамыз
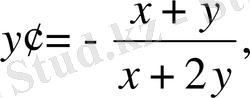
Мұнда
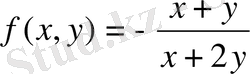 функциясы нөлінші дәрежелі біртекті функция болама соны тексерейік:
функциясы нөлінші дәрежелі біртекті функция болама соны тексерейік:
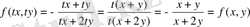
Демек, y=ux алмастыруын жасауға болады.
Сонда
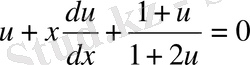
немесе
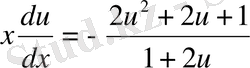
Айнымалыларын бөлу қиын емес
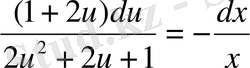
Интегралдаймыз:
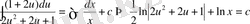
немесе
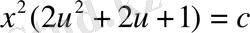
Енді
u
функциясының орнына
 -ты қойып (2) теңдеудің жалпы шешімін аламыз
-ты қойып (2) теңдеудің жалпы шешімін аламыз
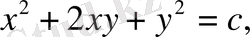 (с>0)
(с>0)
Біртекті теңдеулерге келтірілетін . Дифференциалдық теңдеулерді қарастырамыз. Олар мыналар:
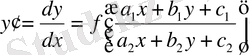 (3)
(3)
Егер
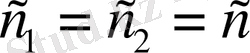 болса, онда (3) теңдеу біртекті болады. Айталық
болса, онда (3) теңдеу біртекті болады. Айталық
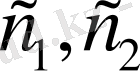 сандарынан біреуі нөлге тең емес болсын. Онда (3) теңдеу біртекті емес, оны біртекті теңдеуге келтіру үшін
сандарынан біреуі нөлге тең емес болсын. Онда (3) теңдеу біртекті емес, оны біртекті теңдеуге келтіру үшін
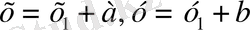 (4)
(4)
алмастыруларын жамаймыз, онда
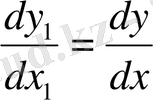 айқын.
айқын.
Бұл геометриялық тұрғыдан қарағанда, координаталар бас нүктесін
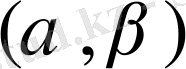 нүктесіне көшірумен пара-пар. Бұл сандарды
нүктесіне көшірумен пара-пар. Бұл сандарды
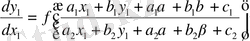 (5)
(5)
теңдеуді біртекті болатындай етіп таңдау керек.
Сондықтан
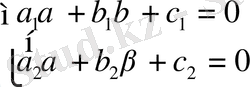 (6)
(6)
сонда
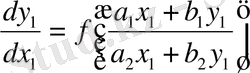
біртекті теңдеу, оның жалпы шешімін
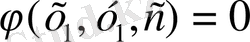 жазылады.
жазылады.
Егер
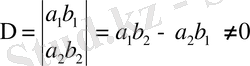 (7)
(7)
болса, онда (6) жүйенің шешімі бар. Осы жүйеден
 мен
мен
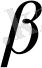 -ны тауып, (4) формулаға қойсақ:
-ны тауып, (4) формулаға қойсақ:
 және
және
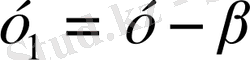 болады. Ендеше (3) теңдеудің жалпы шешімі
болады. Ендеше (3) теңдеудің жалпы шешімі
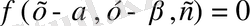 болады:
болады:
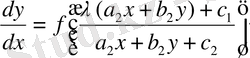 (8)
(8)
(8) теңдеуді
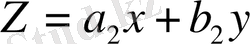 алмастыруды жасап, оны айнымалылары бөлінетін теңдеуге келтіруге болады.
алмастыруды жасап, оны айнымалылары бөлінетін теңдеуге келтіруге болады.
2-мысал. . Дифференциалдық теңдеуді шешеміз:
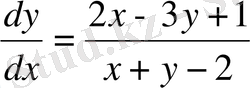 (9)
(9)
Шешуі.
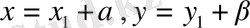 алмастыруын жасаймыз және
алмастыруын жасаймыз және
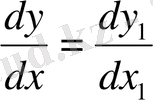 ескерсек (9) теңдеу былай жазылады.
ескерсек (9) теңдеу былай жазылады.
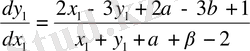
(6) шарт бойынша,
 мен
мен
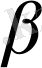 мына жүйенің шешімі болуға тиісті
мына жүйенің шешімі болуға тиісті
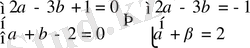
Бұл системаның анықтауышын қарастырамыз
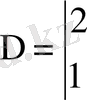
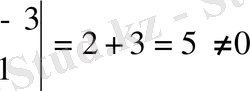 .
.
Демек,
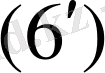 жүйенің шешімі бар:
жүйенің шешімі бар:
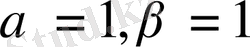 олай болса
олай болса
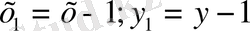
Біртекті теңдеуді шешеміз:
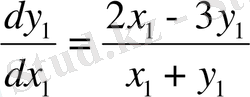
Ол үшін
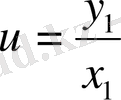 функциясын енгіземіз. Сонда
функциясын енгіземіз. Сонда
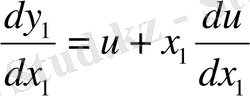
Ендеше
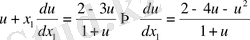
Немесе айнымалыларын бөліп жазсақ
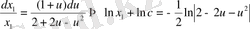
Бұдан
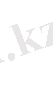
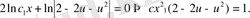
u
функциясының орнына
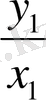 қоямыз:
қоямыз:
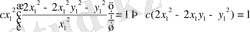
Бұдан
 мен
мен
 -дің орнына қойып берілген (9) теңдеудің жалпы шешімін табамыз:
-дің орнына қойып берілген (9) теңдеудің жалпы шешімін табамыз:
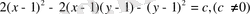
3-мысал. . Дифференциалдық теңдеуді шешеміз:
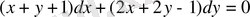
Шешуі. Алдымен бұл теңдеуді былай көшіріп жазамыз:
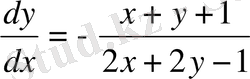 (10)
(10)
Біртекті емес екені көрініп тұр.
Айталық
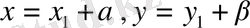 болсын.
болсын.
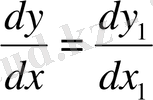 ескеріп (10) теңдеуде
х, у
орнына қоямыз
ескеріп (10) теңдеуде
х, у
орнына қоямыз
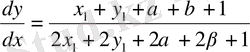
Енді
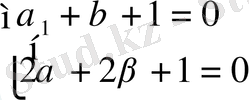 орындалуын талап етеміз. Сонда
орындалуын талап етеміз. Сонда
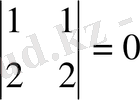
Сондықтан z=x+y алмастыруын жасаймыз.
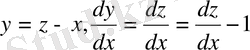
(10) теңдеу енді былай жазылады
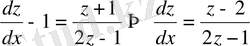
бұл айнымалылары бөлінетін теңдеу:
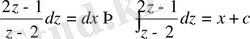
Сонымен
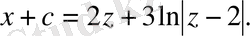
z орнына х+у -ті қойып берілген теңдеудің жалпы шешімін аламыз
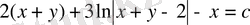
немесе
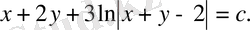
II ТАРАУ
2. 1. Сызықтық теңдеулер
Белгісіз функция мен оның туындысы бойынша сызықты 1- ретті дифференциалдық теңдеуді сызықтық теңдеу деп атайды. Оны жалпы түрде былай жазады
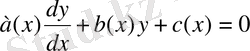 , (1)
, (1)
мұндағы
а(х), b(x), c(x)
, белгілі үзіліссіз функциялар. Қарастырылып отырған х-тің өзгерту аралығында а(х)
 0 деп ұйғарсақ теңдеудің барлық мүшелерін оған бөлуге болады. Сонда (1) берілген теңдеуді төменгі түрде жазуға болады:
0 деп ұйғарсақ теңдеудің барлық мүшелерін оған бөлуге болады. Сонда (1) берілген теңдеуді төменгі түрде жазуға болады:
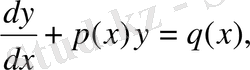 (2)
(2)
мұндағы
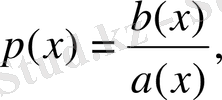
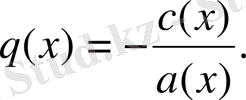
Егер (2) теңдеуде
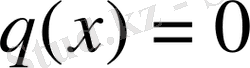 болса, онда
болса, онда
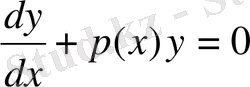 (3)
(3)
теңдеуді біртекті сызықтық деп атайды, егер
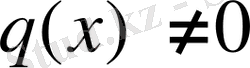 онда (2) біртекті емес теңдеу дейді. (3) теңдеуді (2) біртекті емес сызықтық теңдеу деп те атайды. (3) теңдеу айнымалылары бөлінетін теңдеу болатыны көрініп тұр. Демек оның жалпы шешімі
онда (2) біртекті емес теңдеу дейді. (3) теңдеуді (2) біртекті емес сызықтық теңдеу деп те атайды. (3) теңдеу айнымалылары бөлінетін теңдеу болатыны көрініп тұр. Демек оның жалпы шешімі
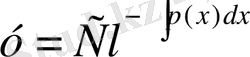 (4)
(4)
Біртекті емес (2) теңдеудің жалпы шешімін тұрақты санды вариациалау әдісімен табуға болады. Оның мағынасы мынадай: біртекті емес (2) теңдеудің шешімі де (4) түрде ізделінеді де, ондағы с тұрақты емес х пен тәуелді белгісіз функция деп есептелінеді. Демек
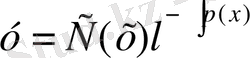 (5)
(5)
Мұндағы С(х) функциясын (5) функция (2) теңдеудің шешімі болатындай етіп анықтайды. (2) теңдеуге (5) формуланы апарып қоямыз:
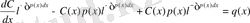
немесе
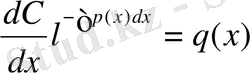
бұдан
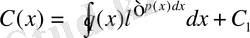 ,
,
мұндағы
 - кез келген тұрақты сан.
С(х)
-тің табылған мәнін (5) формулаға қойып біртекті емес (2) теңдеудің жалпы шешімін аламыз
- кез келген тұрақты сан.
С(х)
-тің табылған мәнін (5) формулаға қойып біртекті емес (2) теңдеудің жалпы шешімін аламыз
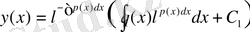
(2) теңдеудің жалпы шешімін төмендегі алмастыру деп аталатын әдіспен де табуға болады. Бұл теңдеудің жалпы шешімін мына түрде іздейміз
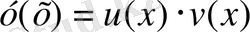
Бұдан
 тауып
у
пен
тауып
у
пен
 мәндерін (2) теңдеуге қоямыз:
мәндерін (2) теңдеуге қоямыз:
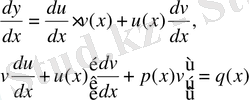
v(x) функцияcын тік жақша ішіндегі өрнек нөлге айналатын етіп таңдап аламыз. Сонда
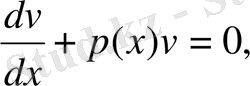 (8)
(8)
онда
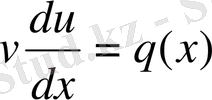 (9)
(9)
(8) айнымалылары бөлінетін теңдеу, оның жалпы шешімі
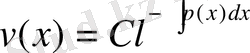 (10)
(10)
Бұл өрнекті v(x) -тің орнына қоямыз
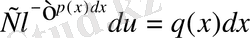
немесе
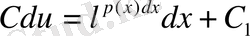 (11)
(11)
мұндағы
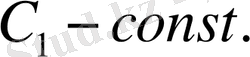
Сонымен (10), (11) өрнекті (7) формулаға қойып берілген (2) теңдеудің жалпы шешімін табамыз
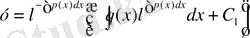
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz