Жазықтықтағы геометриялық салулар: теория, әдістер және орта мектепте оқыту


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 44 бет
Таңдаулыға:
Мазмұны
Кіріспе . . . 3
- Тарау. Жазықтықтағы геометриялық салулар және оларды шешу.
§ 1. Орта мектептегі геометриялық салулар . . . 5
§2. Жазықтықтағы нүктелердің геометриялық
орындары (НГО) . . . 8
§3. Нүктелердің геометриялық орындар әдісімен салу
есептерін шешу . . . 18
- Тарау. Геометриялық салу есептеріне қиылысу және алгебарлық әдістерді пайдалану.
§1. Алгебралық өрнектерді салу . . . 30
§2. Салу есептерін алгебралық әдіспен шешу . . . 33
- Қорытынды . . . 44
Кіріспе
Мектеп геометриясының негізгі материалдарының бірі-геометриялық салулар. Бастауыш сыныптан бастап, кеңістіктің әр түрлі қасиетін сипаттайтын геометрияның абстрактілі тарауларына дейін фигураларды салу кездеседі. Мұндай конструктивті геометрияны б. э. д. III-IV ғасырларда өмір сүрген грек математиктері Евклид, Архимед, Аполлоний және ежелгі Отырар шахарында туған қазақ математигі Әл-Фараби (870-950) дамытқан.
Жоғары математиканың негізін салған ағылшын математигі әрі физигі
И. Ньютон (1643-1727), неміс математиктері Г. В. Лейбниц(1646-1650) пен
К. Ф. Гаусс (1744-1808), француз математигі Р. Декарт(1596-1650), швейцария
математигі А. Эйлер (1707-1783) т. б. Конструктивтік есептерге ерекше көңіл
бөлген. Геометриялық салулар теориясы И. И. Александровтың
Н. Ф. Четверхиннің, Б. И. Аргуновтың, Ж. Адамардың т. б. еңбектерінде
эерттелген, ал оны оқыту әдістемесі жөнінде Д. И Перепелкиннің, Г. Л. Сенниковтың, Г. Г. Маслованың т. б. еңбектері бар.
Геометрия тарихынан математиканың аса маңызды тараулары
геометриялық салуларға тәуелді болғанын білеміз. Геометриялық салулар теориясы геометрияның негізгі салалары: аналитикалық геометрия, проективтік геометрия, сызба геометрияның пайда болуына байланысты жоғары дәрежеде дами бастады.
Салу есебі физика жэне сызу пәндерімен де тығыз байланысты. Физикалық шамалардың өзгерісін графиктік жолмен сипаттауға салу есептері қолданылады. Сызу сабағында оқушылар геометриялық фигураларды салудың кейбір әдістерін нақты практикалық істерінде пайдаланады. Инженерлер мен техниктер кейбір практикалық жұмыстарды графиктер мен сызбалардың көмегімен орындайды. Техниканы дамытуда сызба геометрия, геометриялық салулар, сызбалардың теориясы өте зор рөл атқарады.
Зерттеудің мақсаты . Жазықтықтағы геометриялық салуларды орта мектепте жаңа ақпаратты технологияға байланыстыра оқыту және оқушылардың теориялық және практикалық білімі мен біліктілігін қалыптастыру.
Зерттеудің болжамы . Жазықтықтағы геометриялық салу есептерін шешудің әдістерін (НГО және алгебралық әдістер) үйрету арқылы оқушылардың білімін белгілі бір жүйеге қалыптастыра отырып, олардың логикалық ойлау қабілетін жетілдіру.
Зерттеудің пәні . Жазықтықтағы геометриялық салу есептерін шешуді орта мектеп оқушыларына үйрету.
Зерттеу нысаны (объектісі) . Студенттердің педагогикалық практика өткізетін орта мектеп оқушылары мен математика пәнінің мұғалімдері.
Зерттеудің міндеттері .
- Оқытудың жаңа технологияларының элементтерін енгізу.
- НГО және алгебралық әдістердің негізгі критериясын анықтау.
- Сабақ сапасын арттыру арқылы, оқушылардың ізденуін және таным деңгейін жоғарылату.
I-тарау. Жазықтықтағы геометриялық салулар және оларды шешу әдісітері.
§1. Орта мектептегі геометриялық салулар.
Салу есебі деп, берілген элементтер бойынша геометриялық құралдардың (сызғыш пен циркуль) көмегімен белгілі бір шартты қанағаттандыратын геометриялық фигураларды салуды айтады.
Геометриялық фигураларды салуға V-VI сыныптардан бастап көңіл бөліне бастайды. Циркуль мен сызғышты пайдаланып әр түрлі фигураларды салу орындалады. Геометриялық фигураларды салу қарастырғанда, планиметрияның негізгі курсын оқып үйренуге оқушыларды алдын-ала дайындау мақсаттары көзделген.
VII сыныптағы "Геометриялық салулар"тақырыбы V-VI сыныптағы материалдармен сабақтас, бірақ салуларға ерекше назар аударылып
өтіледі. Үшбұрыштарды салудың әртүрлі жағдайлары қарастырылады. Үшбүрышты салу мүмкін болу үшін, а+в>с және а-в <с теңсіздіктерінің орындалуы қажет
Берілген бұрышқа тең бұрыш салу, бұрыштың бессектрисасын салу, кесіндіні қақ бөлу, берілген түзуге перпендикуляр түзу салу, нүктелердің геометриялық орындары, геометриялық орындарға есептер, шеңберге іштей сызылған бұрыштар - «Геометриялық салулар» тақырыбына қарастырылады. Осы тақырыпта 30 салу есептері бар.
Сонымен, мектеп математика курсында қарастырылған негізінен жай салулар екен. Жай салуларға төмендегі есептер жатады:
1) берілген α бұрышына тең бұрыш салу;
2) берілген АВ түзуіне, одан тысқары жатқан С нүктсінен перпендикуляр салу;
3) берілген бұрышты тең екіге бөлу. /бұрыштың биссектрисасын салу/;
4) берілген АВ кесіндісін екіге бөлу; .
5) берілген АВ түзуіне, одан тысқары жатқан С нүктесінен параллель жүргізу;
6) . берілген түзудің бойына, берілген кесіндіге тең кесінді салу;
7) берілген а және b кесінділерінің қосындысына тең кесінді салу;
8) берілген а кесіндісінен берілген b кесіндісін алу /а>b/;
9) берілген кесіндіні берілген қатынасқа бөлу;
10) берілген үш қабырғасы бойынша үшбүрыш салу;
11) берілген қабырғасымен сол қабырғаға іргелес екі бұрышы бойынша үшбұрыш салу;
12) берілген екі қабырғасы және сол қабырғалардың арасындағы бұрыш бойынша үшбұрыш салу;
13) берілген гипотинузасы мен катеті бойынша тік бұрышты үшбұрыш салу және т. б.
Элементар салулардың 1-6 есептері негізгі салулар деп аталады. Негізгі салулар деп, алдыңғы уақытта кездесетін геометриялық салу есептерін шешуге негіз болатын есептерді айтамыз.
Салу есептерін циркуль мен сызығыштың жәрдемімен шешу үшін, оны төмендегі әр уақытта шешілетін бес түрлі салу есептерінің біріне келтіруіміз керек:
а) белгілі екі нүкте арқылы түзу сызық салу ;
ә) белгілі екі түзудің қилысу нүктесін салу/егер бұл нүкте бар болса/;
б) белгілі нүктені центр етіп алып, белгілі радиуспен шеңбер салу;
в) белгілі түзу мен белгілі шеңбердің қиылысу нүктелерін салу/егер бұл
нүктелер бар болса/;
г) белгілі екі шеңбердің қиылысу нүктелерін салу /егер бүл нүктелер
болса/
Геометриялық салу есептерін шешу белгілі жүйе (система) бойынша орындалады. Шешудің классикалық схемасы, негізінен 4 кезеңнен тұрады: 1) анализ(талдау) ;
2) салу (синтез) ;
3) дәлелдеу;
4) зерттеу,
Геометриялық салу есептерін шешкенде, оның барлық мүмкін шешуін табу үшін осы схема бойынша орындау керек.
Геометриялық салу есебін шешудегі негізгі кезең - анализ . Анализдің максаты-есептің шешу әдісін іздеу. Анализдің мәні -салу есебінің берілген элементтері мен ізделінетін элементтерінің арасындағы байланысты табу. Салу есебіне анализ жасағанда, сол есепті шешілген деп ұйғару керек. Бұл ұйғарудың графиктік түрі, есептің шартына сәйкес фигураны кескіндеу болып табылады. Көмекші чертежге /кескініне/ қарап ізделінетін чертежді қалай салу керек екендігін біле бермейміз, мұндай жағдайда көмекші чертежде салуға болатын кейбір бөлігін салу арқылы ізделінетін фигураны саламыз. Есепке анализ жасағанда қажетті теоремаларды және элементар геометриялық салуларды пайдалану қажет.
Геометриялық салу есебіне анализ жасағаннан кейін, есеп шартына байланысты фигураны сала бастаймыз. Ізделінетін фигураны салу үшін, салу жұмысын біртіндеп орындаймыз. Салу кезінде анализ жасағандағы талдаулар кері ретпен орындалады, олай болса бұл кезеңді синтез деп атауға болады. Салу кезеңінің нәтижесі ізделінетін фигураның чертежі болып табылады.
Салу есебін шешу процесіндегі дәлелдеу кезеңінде салынған фигураның ізделінетін фигура болатындағына логикалық талдау жасалынады. Дәлелдеу кезеңінде жасалынған талдаулардың дұрыстығын анықтаймыз, яғни салынған фигура, есептің шартын толық көз жеткіземіз .
Салу есебін шешуді анықтайтын маңызды кезең- зерттеу . Бұл кезеңнің негізгі мақсаты, есептің шешуін толықтыру. Зерттеу кезеңінде, есептердің шешімдерінің саны мен ізделінетін фигураның болу шарттары анықталады.
Аталған мәселенің өзектілігі, ғылыми- теориялық және әдістемелік негіздерін айқындау зерттеу жұмысымыздың негізгі мәселесі болып табылады. Осыған орай зерттеу жұмысымыздың тақырыбын “Жазықтықтағы геометриялық салулардың теориясы мен практикасы” деп таңдауымызға себеп болды.
§2. Жазықтықдағы нүктелердің геометриялық орындары.
Ортақ қасиетке ие болатын барлық нүктелердің жиынын нүктелердің геометриялық орны дейді.
1. Берілген О нүктесінен r қашықтықта жататын нүктелердің жиыны, центрі О нүктесінде жатқан, радиусы r-ге тең шеңбер болады (1-сызба) .

1сызба
2. Кесіндінің ортасы арқылы жүргізілген перпендикуляр сол кесіндінің ұштарынан бірдей қашықтықта жататын нүктелердің жиыны болады
(2-сызба) .
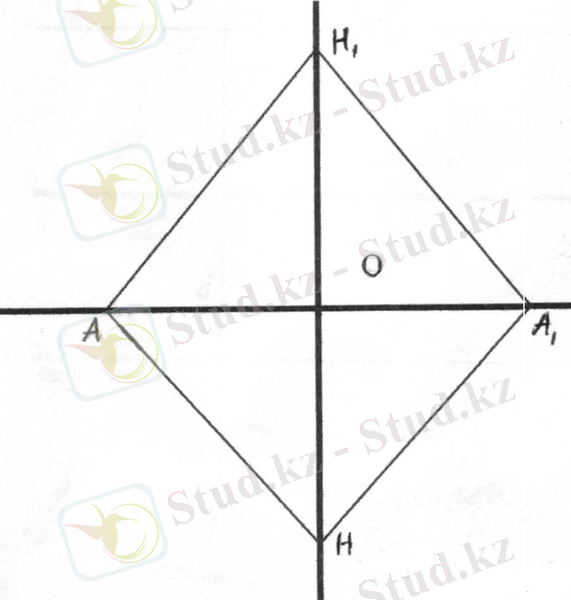
2-сызба
3. Берілген түзуден Н қашықтықта жататын нүктелердің жиыны берілген түзуге параллель және оның екі жағынан Н қашықтықта жүргізілген екі түзу болады (3- сызба) .
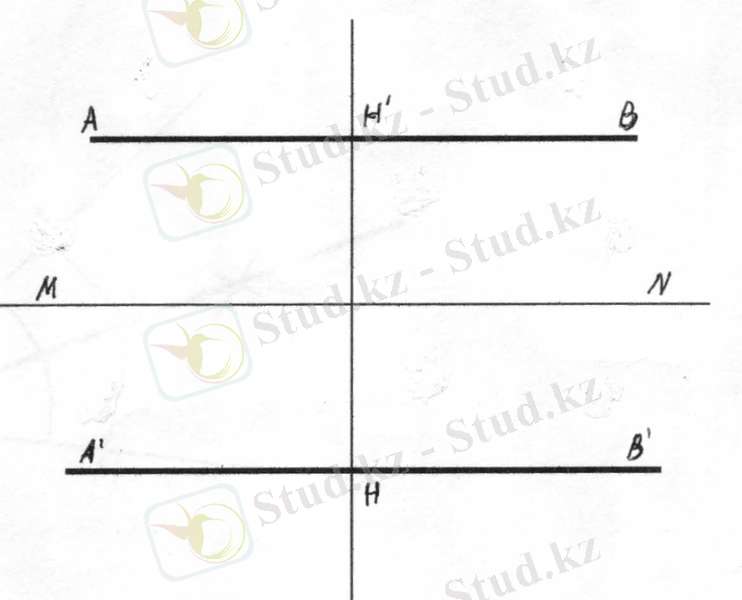
3-сызба
4. Берілген екі параллел түзуден d қашықтықта жататын нүктелердің жиыны берілген екі түзуге де параллел - сол түзулердің арасында жататын және әрқайсысынан d қашықтықта жүргізілген түзу болады (4- сызба) .

4 сызба
5. Бұрыштың биссектрисасы деп сол бұрыштың қабырғалары бірдей қашықтықта жататын нүктелердің жиыны болады (5- сызба) .
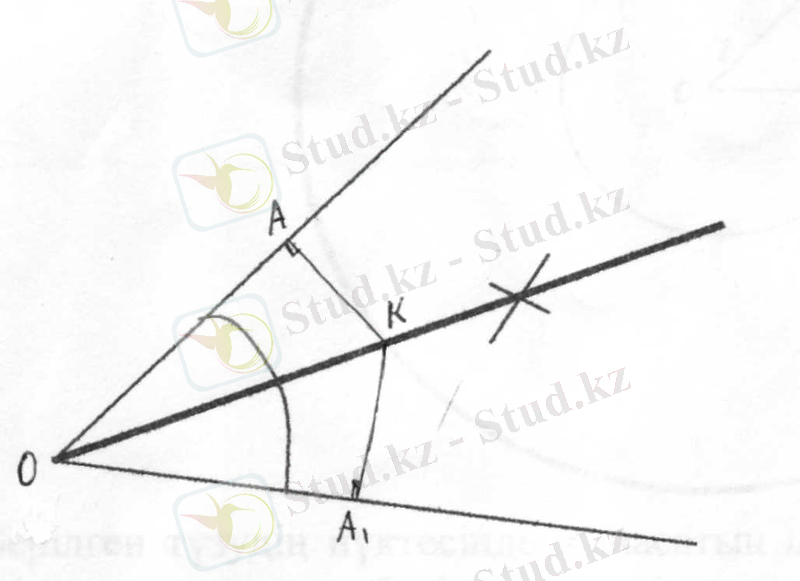
5 сызба
6. Берілген О нүктесінен өтетін, радиусы R-re тең шеңберлердің центірлердің жиыны
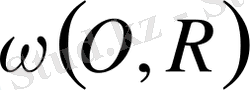 шеңбер болады (6- сызба) .
шеңбер болады (6- сызба) .
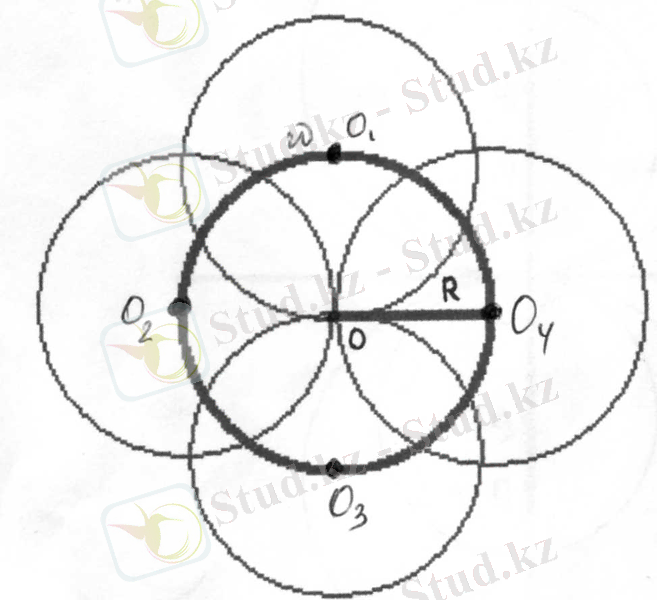
6 сызба
7. Берілген
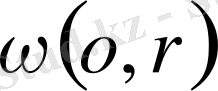 шеңбері жанамасының байында және жанасу нүктесінен d қашықтықта жататын нүктелердің жиыны радиусы R шеңбер болады (7 -сызба) .
шеңбері жанамасының байында және жанасу нүктесінен d қашықтықта жататын нүктелердің жиыны радиусы R шеңбер болады (7 -сызба) .

7 - сызба
8. Берілген түзудің нүктесінде жанасатын шеңберлердің центірлерінің жиыны берілген түзуге оның берілген нүктесі арқылы жүргізілген перпендикуляр түзу болады (8- сызба) .

8 сызба
9. Берілген екі нүкте арқылы өтетін шеңбердің центірлерінің жиыны сол берілген нүктелер арқылы жүргізілген кесіндіге оның ортасы арқылы жүргізілген перпендикуляр болады (9- сызба) .

9 - сызба
10. Екі қилысатын түзулерінің екеуімен де жанасатын шеңберлердің центірлерінің жиыны сол берілген екі түзумен анықталатын бұрыштардың биссектрисалары болады (10- сызба) .
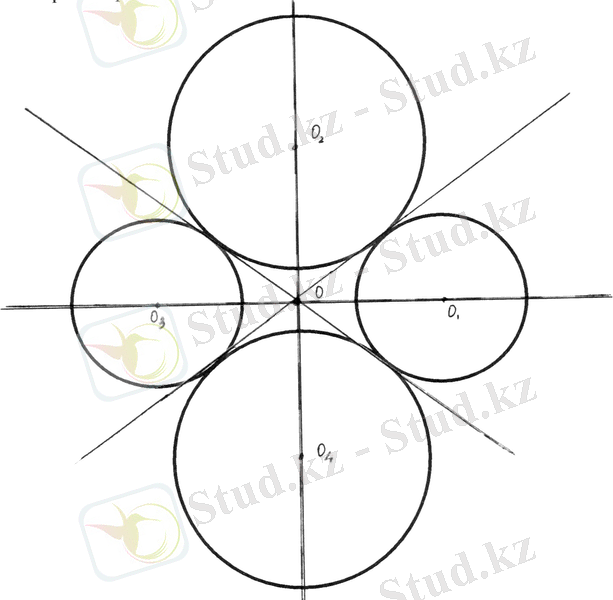
10 - сызба
11. Берілген R радиуспен берілген
 шеңберді тең екіге бөлетін шеңберлердің центірінің жиыны радиусы
шеңберді тең екіге бөлетін шеңберлердің центірінің жиыны радиусы
 -ге тең, сол шеңбермен концентрлі шеңбер болады (11- сызба) .
-ге тең, сол шеңбермен концентрлі шеңбер болады (11- сызба) .

11- сызба
12. Берілген бұрыштардың екі қабырғасынан да тең хордалар қиятын шенберлердің центрлерінің жиыны сол бұрыштың биссектрисасы болады (12-сызба) .

12 - сызба
13. Берілген
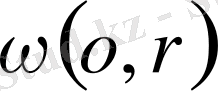 шеңберімен оның берілген М нүктесінде жанасатын шеңберлердің центірінің жиыны ОМ түзуі болады (13-сызба) .
шеңберімен оның берілген М нүктесінде жанасатын шеңберлердің центірінің жиыны ОМ түзуі болады (13-сызба) .
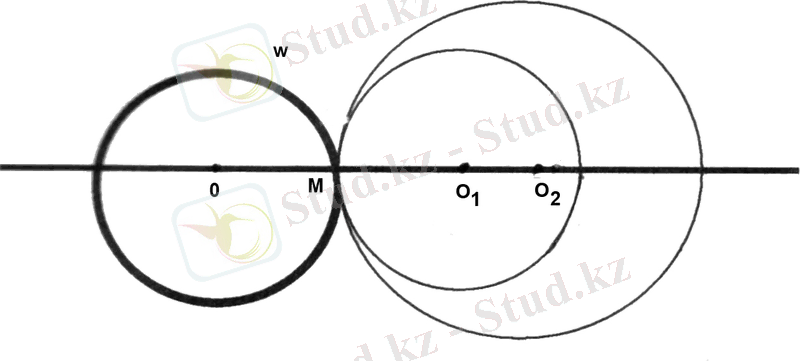
13 - сызба
14. Берілген
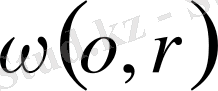 шеңбері берілген α бұрышпен көрінетін нүктелердің жиыны сол шеңберге концентірлі шеңбер болады, берілген бұрыш деп А нүктесінен шеңберге жүргізілген екі жанаманың арасындағы бұрышты айтады (14- сызба) .
шеңбері берілген α бұрышпен көрінетін нүктелердің жиыны сол шеңберге концентірлі шеңбер болады, берілген бұрыш деп А нүктесінен шеңберге жүргізілген екі жанаманың арасындағы бұрышты айтады (14- сызба) .

14 - сызба
15. Берілген кесінді тік бұрышпен көрінетін нүктелердің жиыны
 шеңбері болады (15 сызба) .
шеңбері болады (15 сызба) .

15 - сызба
16. Табанындағы бұрышы АВС=β, ол табаны ВС болатын үшбұрыштың A төбелерінің жиыны табанымен β бұрыш жасайтын және В нүктесінен шығатын екі сәуле болады (16 сызба) .

16 - сызба.
17. Жазықтықтағы берілген екі нүктеден ара қашықтықтарының қосындысы әрқашанда бірдей санға тең болатын нүктелер жиыны ЭЛЛИПС деп аталады( 17-сызба) .
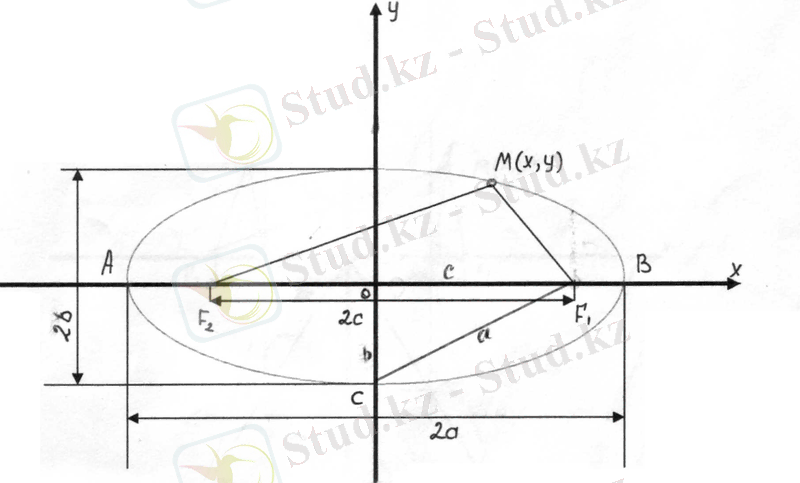
17 - сызба
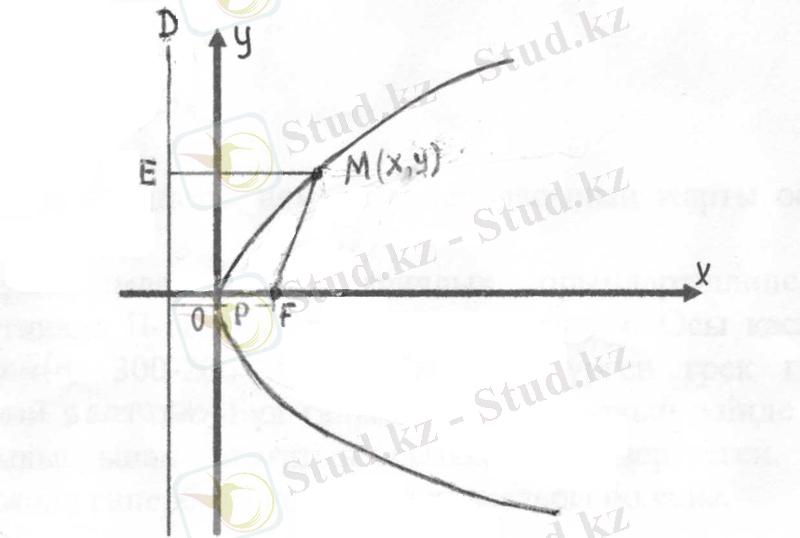
15. Жазықтықта жатқан белгілі бір Ғ нүктеден және бір D түзуден бірдей қашықтықта жататын нүктелер жиыны ПАРАБОЛА деп аталады (18- сызба), яғни MF=ME
18 - сызба
Ғ нүктесін параболаның фокусы, ал D директрисасы деп аталады. Ғ нүктесі арқылы өтетін директрисаға перпендикуляр түсуді параболаның өсі деп атайды. Фокустан директрисаға дейінгі ара қашықтықты параболаның параметрі p деп атайды. Параболаның анықтамасы бойынша ҒМ=ЕМ.
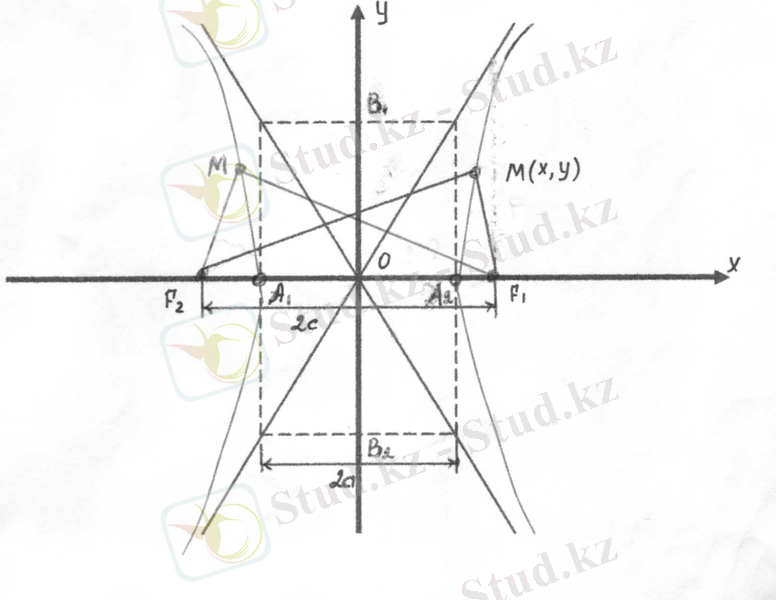
19. Жазықтық бойында берілген екі нүктеден ара қашықтарының айрымы әрқайсысы бір тұрақты санға тең нүктелердің жиынын ГИПЕРБОЛА деп атайды (19- сызба),
 .
.
 19- сызба
19- сызба
Жазықтықтың бойында берілген екі нүкте F
 және Ғ
және Ғ
 эллипстің және гиперболаның фокустары деп атайды. Эллипс және гиперболаның анықтамасы бойынша әрқашанда
эллипстің және гиперболаның фокустары деп атайды. Эллипс және гиперболаның анықтамасы бойынша әрқашанда
F
 М+ Ғ
2
М =2а
М+ Ғ
2
М =2а
Ғ
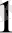 М-Ғ
М-Ғ
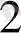 М=2а
М=2а
а-тұрақты шама, оны эллипстің немесе гипеболасының жарты өстері деп атайды.
Жоғарыдағы тұжырымдарға геометриялық орындар: эллипс, парабола, гипербола математикада ІІ-ретті қисықтар деп аталады. Осы қасиеттерді біздің эрамызға дейін 300-200 жылдары өмір сүрген грек ғалымдары Архимед, Апаллоний зерттеген. Бұл ғалымдар сол уақыттың, өзінде конустың жазықтықпен қиылысуынан шығатын сызықтарды зерттеген. Дөңгелек эллипс, парабола және гипербола конустың қималары болады.
§3. Нүктелердің геометриялық орындар әдісімен салу есептерін шешу.
1-есеп. Берілген ω
 (
(
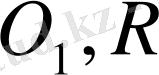 ) және ω
) және ω
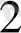 (
(
 ) шеңберлеріне ортақ сыртқы жанама жүргізу.
) шеңберлеріне ортақ сыртқы жанама жүргізу.
Нүктелердің геометриялық орындар әдісі мен параллель жылжыту әдісі бірге қолданылатын жағдайды қарастырамыз.
Анализ.
А
 А
А
 -іздеп отырған ортақ жанама болсын. Оны салу үшін жанасу нүктесінің біреуін табу керек. Мысалы: А
-іздеп отырған ортақ жанама болсын. Оны салу үшін жанасу нүктесінің біреуін табу керек. Мысалы: А
 табайық. А
табайық. А
 нүктесінің бір қасиеті белгілі, ол ω
нүктесінің бір қасиеті белгілі, ол ω
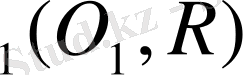 шеңбердің бойында жатады. Оның екінші қасиеті
шеңбердің бойында жатады. Оның екінші қасиеті
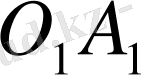 сәулесінің бойында жатады. Ол сәулені жүргізу үшін бір К нүктесін табу керек. Ол үшін
сәулесінің бойында жатады. Ол сәулені жүргізу үшін бір К нүктесін табу керек. Ол үшін
 -ні
-ні
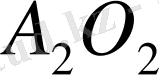 бағытымен ұзындығы сол
бағытымен ұзындығы сол
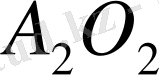 -ге тең қашықтықта параллель жылжытамыз. Егер К нүктесі табылса, онда есеп шешіледі. К-ны іздейміз. Сызбадағы
-ге тең қашықтықта параллель жылжытамыз. Егер К нүктесі табылса, онда есеп шешіледі. К-ны іздейміз. Сызбадағы
 және
және
 болғандықтан
болғандықтан
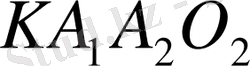 параллелограмм. Сондықтан
параллелограмм. Сондықтан
 , яғни К нүктесінің О
, яғни К нүктесінің О
 -ден қашықтығы R-r. Бұл К нүктесінің бір қасиеті
-ден қашықтығы R-r. Бұл К нүктесінің бір қасиеті
 К нүктесін
К нүктесін
 тік бұрышпен көрінеді. (2-қасиеті: іштей сызылған жанама R+r ) .
тік бұрышпен көрінеді. (2-қасиеті: іштей сызылған жанама R+r ) .

Салу.
 мен
мен
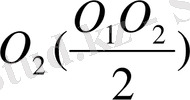 шеңберін жүргізіп, К нүктесін табамыз.
шеңберін жүргізіп, К нүктесін табамыз.
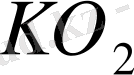 және
және
 жүргізіп, А
жүргізіп, А
 мен А
мен А
 нүктелерін табамызда түзумен қосамыз.
нүктелерін табамызда түзумен қосамыз.
Дәлелдеу.
АА
 түзуі О
түзуі О
 мен О
мен О
 шеңберіне жанама болады, себебі салу бойынша
шеңберіне жанама болады, себебі салу бойынша
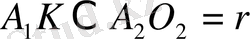 ,
,
 , олай болса
, олай болса
 параллелограмм және
параллелограмм және
 , А
, А
 нүктесі О
нүктесі О
 шеңбері, А
шеңбері, А
 нүктесі О
нүктесі О
 шеңберіне тән.
шеңберіне тән.
Зерттеу. Шеңберлер жазықтықта әр түрлі орналасады.


Шешуі жоқ. Шешуі біреу.
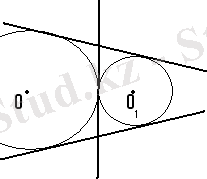
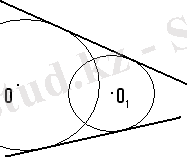
3-шешуі бар. 2-шешуі бар.
2-есеп. Радиустары r және
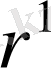 -ке
тең берілген екі шеңберді жанайтын шеңберлер жүргізіңіз (r>r
-ке
тең берілген екі шеңберді жанайтын шеңберлер жүргізіңіз (r>r
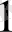 )
)
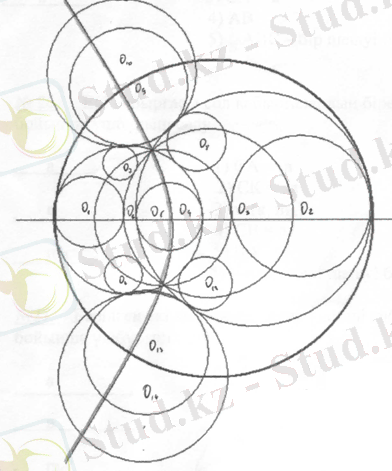
Есептің шешуін табу үшін берілген екі шеңбермен де жанасатын шеңберлердің центрлерін іздеу керек. Бұл шеңберлердің центрлері берілген екі шеңбердің де бірдей қашықтықта жатады.
Іздеп отырған шеңбердің радиусын R
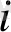 мен (і= 1, 2, 3 . . . ) , ал берілген шеңберлердің центірлерінің ара қашықтығы d мен берейік. Есептің шешуінің саны берілген шеңбердің жазықтықта орналасуына байланысты. Есепке зерттеу жүргізу арқылы салуды орындайық.
мен (і= 1, 2, 3 . . . ) , ал берілген шеңберлердің центірлерінің ара қашықтығы d мен берейік. Есептің шешуінің саны берілген шеңбердің жазықтықта орналасуына байланысты. Есепке зерттеу жүргізу арқылы салуды орындайық.
1. d=0, екі шеңберді де жанайтын шеңберлердің радиустары бірдей болады, яғни R=r-r/2 ал ол шеңберлердің центірлері берілген екі шеңберге де концентрлі шеңбердің бойында жатады, шексіз көп шешуі бар (1 сызба) .
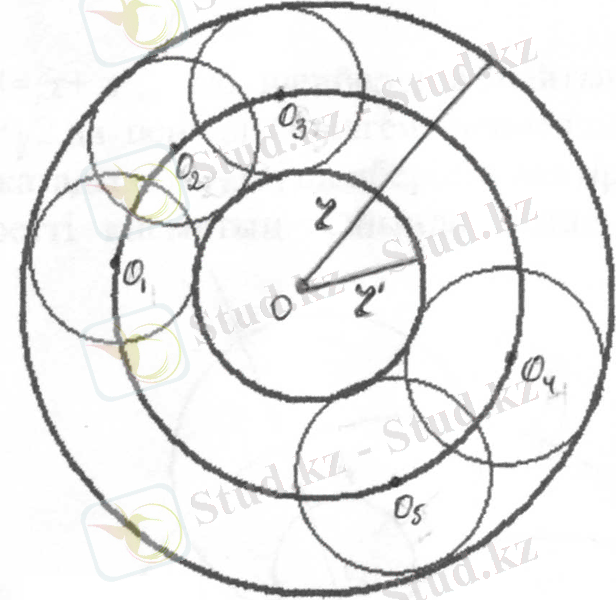
1 - сызба
2. d>r+r' екі шеңбердіде жанайтын
 және
және
 щеңбердің радиустары
щеңбердің радиустары
 ал центірлері берілген шеңберлердің центірлерін қосатын түзудің бойында жатады.
ал центірлері берілген шеңберлердің центірлерін қосатын түзудің бойында жатады.
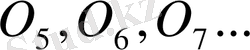 - шеңберлердің центірлері болатын екінші ретті қисықтың бойында жатады, шексіз көп шешуі бар (2-сызба) .
- шеңберлердің центірлері болатын екінші ретті қисықтың бойында жатады, шексіз көп шешуі бар (2-сызба) .
2 - сызба
3. d= r+ r
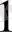 екі шеңберді жанайтын О
екі шеңберді жанайтын О
 шеңбердің радиусын R
шеңбердің радиусын R
 =d+(r+ г') /2, ал центірі берілген шеңбердің центірін қосатын түзудің бойында жатады.
=d+(r+ г') /2, ал центірі берілген шеңбердің центірін қосатын түзудің бойында жатады.
 шеңберінің центірлері төбесі k нүктесі болатын екінші ретті қисықтың бойында жатады, шексіз көп шешімі бар (3-сызба) .
шеңберінің центірлері төбесі k нүктесі болатын екінші ретті қисықтың бойында жатады, шексіз көп шешімі бар (3-сызба) .

3 - сызба
- d<r+екі шеңберді жанайтын O
- d=rшеңбердің радиусы R=d+(r+ r') /2
- d<r
екі шеңберді сырттай іштей жанайтын шеңбердің центрлері мен О шеңберді іштей жанайтын, О
 шеңберді сырттай жанайтын шеңбердің центірлері екінші ретті қисықтың бойында жатады, шексіз көп шешуі бар (4-сызба) .
шеңберді сырттай жанайтын шеңбердің центірлері екінші ретті қисықтың бойында жатады, шексіз көп шешуі бар (4-сызба) .
4 - сызба
5. d<r екі шеңберді жанайтын шеңберлердің центрлері шеңбердің бойында жатады, шексіз көп шешуі бар (5 сызба) .
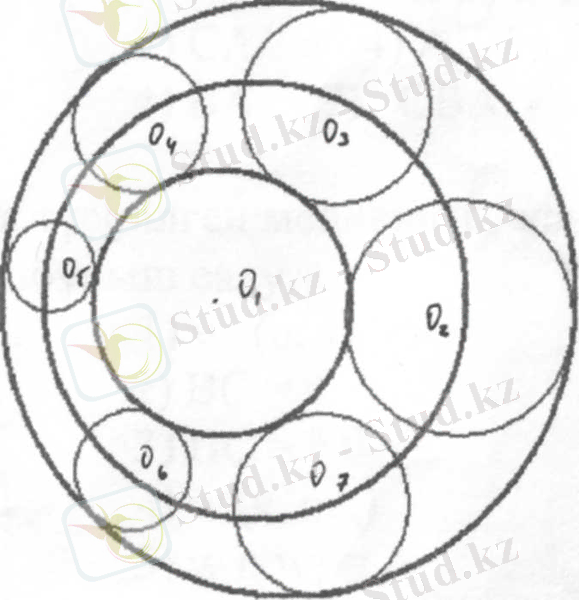 5 - сызба
5 - сызба
Бұған дейін салу есебін шығарудағы ортақ схемасын бердік. Сонымен қатар салу есебін шығаруда негізінен келесі әдістер қолданылады: қиылысу әдісі, түрлендіру әдісі, алгебралық әдіс және басқа әдістер. Салу есептері бұл әдістермен шектеліп қоймайды, бұдан да басқа әдістері бар.
Қейбір есептерді шығаруда жекелей әдістерді табуда табандылық пен қажырлық керек.
1-есеп. Екі қабырғасы сол қабырғалардың біреуіне түсірілген медиана бойынша үшбұрыш салу.
I. Анализ.
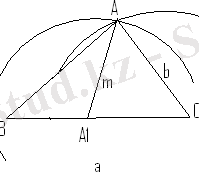
АВС ізделінген үшбұрыш болсын.
ВС кесіндісінің ортасы - А1 нүктесі болсын, ВС=a, АС=b болсын. Егер ВС кесіндісін салсақ, онда ізделген үшбұрыштың екі төбесі, В және С төбелері белгілі болады да, А төбесін салу ғана қалады. А төбесінен А1 нүктесіне дейінгі қашықтық m-ға тең болғандықтан, А нүктесі центрі А1 нүктесі, ал радиусы m болатын ω(А1, m) шеңберінде жатады. Осы сияқты А төбесінен С төбесіне дейінгі қашықтық b кесіндісіне тең болғандықтан, А нүктесі центрі С нүктесі, ал радиусы b-ға тең болатын ω(С, b) шеңберінде жатады. Сонымен:
α) A€ω(A1, m) ; β) A€ω(C, b) .
II. Салу.
1) BC=a кесіндісін (сызба) ;
2) ВС кесіндісінің ортасы А1 нүктесін;
3) Центрі А1 нүктесі, радиусы m болатын ω(А1, m) шеңбірін;
4) Центрі С нүктесі, радиусы b болатын ω(C, b) шеңберін;
5) ω(A, m) ω(C, b) ={A, A^};
6) A және A^ нүктелерін В және С нүктелерімен қосамыз.
АВС және A^BC үшбұрыштары ізделінді үшбұрыштар.
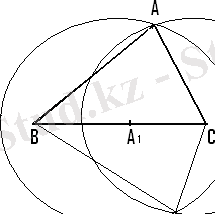 2-сызба.
2-сызба.
III. Дәлелдеу.
- ВС=a салуымыз бойынша;
- ω1(А1, m), ω2(C, b) шеңберлері де салуымыз бойынша;
- А нүктесі ω1 және ω2 шеңберлеріне тиісті болғандықтан АВС және А^ВС үшбұрыштары ізделінген үшбұрыштар.
IV. Зерттеу.
1) және 4) салулары бір мәнді, ω1 және ω2 шеңберлері қиылысуы үшін, демек, АВС үшбұрышы салынуы үшін үшбұрыштар теңсіздігінің орындалуы қажет:
b<m+a/2
Сонымен, егер b>m+a/2 болса, онда есептің шешімі жоқ; егер b<m+a/2, m<b+a/2, a/2<b+m болса, онда есептің бір шешімі бар.
2-есеп. Екі қабырғасы және сырттай сызылған шеңбердің радиусы бойынша үшбұрыш салу.

- w (o, R)
- CB=a
- CF=b
- AB
- ABC-бір шешуі бар
4-есеп. Берілген екі қабырғасы және үшінші қабырғаға түсірілген медиана бойынша үшбүрыш салу.
- CD=2 m
- а, в және 2 m- үшбұрыш салу
a. CA=b
b. w(C, 2m
)
c. w

d.
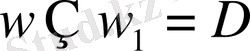
3. CA\\n
4. AD\\m
5. n

6. BA
7. CBA
5-есеп. Берілген қабырғасы сол қабырғаға түсірілген медианасы және сырттай сызылған шеңбердің радиусы бойынша үшбұрыш салу.
- w
 BC=a
BC=a
- BC=KC
- W (k, m)
- w nq
- АС және АВ
- ВС екі шешуі бар
6-есеп. Екі қабырғасы және үшінші қабырғаға түсірілген биіктік бойынша үшбұрыш салу.
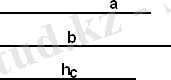
- AC=b
- OA=OC
- w(O, OA)
- w
- AB
- w
- c
- BC
- АВС екі шешуі бар
7-есеп. Гипотенузасы және тік бұрышынан гипотенузаға түсірілген биіктігі бойынша тік бұрышты үшбұрыш салу.
- AB=c
- Ao=oB
- w(o, oA)
- AB h
- AB\\MN
- w MN
- СА және СВ
- АВС 4 шешуі бар
Өзіндік жұмысқа арналған салу есептері.
1-есеп. Берілген үш түзуді де жанайтын шеңберлер жүргізу.
2-есеп. Берілген табан қабырғасы және бүйір қабырғаларына түсірілген биіктіктер бойынша үшбұрыш салу.
3-есеп. а қабырғасы,
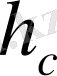 биіктігі, А бұрыш бойынша үшбұрыш салу.
биіктігі, А бұрыш бойынша үшбұрыш салу.
4-есеп.
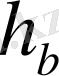 биіктігі,
биіктігі,
 және
және
 медианалары бойынша үшбұрыш салу.
медианалары бойынша үшбұрыш салу.
5-есеп. В бұрышы, с қабырғасы және басқа екі қабырғасының қосындысы (а+в) бойынша үшбұрыш салу.
6-есеп. В бұрышы,
 биіктігі және 2р периметрі бойынша үшбұрыш салу.
биіктігі және 2р периметрі бойынша үшбұрыш салу.
7-есеп. h биіктігі, d диогоналы бойынша ромб салу.
8-есеп. а қабырғасы
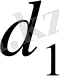 және
және
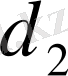 диогоналдары бойынша параллелограмм салу.
диогоналдары бойынша параллелограмм салу.
9-есеп.
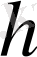 биіктігі
биіктігі
 және
және
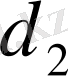 диогоналдары бойынша параллелограм салу.
диогоналдары бойынша параллелограм салу.
10-есеп. А мен Д бұрыштары, а қабырғасы және
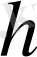 биіктігі бойынша трапеция салу.
биіктігі бойынша трапеция салу.
11-есеп. Табан қабырғаларының айырымы (а-в) бүйір қабырғалары n мен m және d диогоналы бойынша трапеция салу.
12-есеп. а қабырғасы,
 биіктігі және R (үшбұрышқа сырттай сызылған шеңбердің радиусы) бойынша үшбұрыш салу.
биіктігі және R (үшбұрышқа сырттай сызылған шеңбердің радиусы) бойынша үшбұрыш салу.
13-есеп. а қабырғасы және R (үшбұрышқа сырттай сызылған шеңбердің радиусы) бойынша тең бүйірлі үшбұрыш салу.
14-есеп.
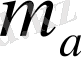 медианасы
медианасы
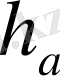 және
және
 биіктіктері бойынша үшбұрыш салу.
биіктіктері бойынша үшбұрыш салу.
15-есеп. а қабырғасы, С бұрышы және қабырғаларының қатынасы(а:в=m:n) бойынша үшбұрыш салу.
16-есеп. А бұрышы,
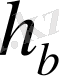 биіктігі және қабырғаларының қатынасы(в:с=m:n) бойынша үшбұрыш салу.
биіктігі және қабырғаларының қатынасы(в:с=m:n) бойынша үшбұрыш салу.
17-есеп. А бұрышы,
 және
және
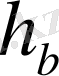 биіктіктері бойынша үшбұрыш салу.
биіктіктері бойынша үшбұрыш салу.
18-есеп. а қабырғасы және
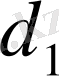 диогоналы бойынша ромб салу.
диогоналы бойынша ромб салу.
19-есеп. а қабырғасы,
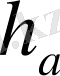 биіктігі және
биіктігі және
 медианасы бойынша үшбұрыш салу.
медианасы бойынша үшбұрыш салу.
20-есеп. а қабырғасы,
 биіктігі және
биіктігі және
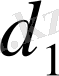 диогоналы бойынша параллелограм салу.
диогоналы бойынша параллелограм салу.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz