Туынды мен дифференциал: анықтамасы, геометриялық және механикалық мағыналары, біржақтық және ақырсыз туындылар


Жоспар
І. Кіріспе
ІІ. Негізгі бөлім
- Туынды ұғымына келтіретін есептер.
- Туындының анықтамасы.
- Туындының геометриялық және механикалық мағыналары.
- Туындысы болатын функцияның үзіліссіздігі.
- Бір жақтық туындылар мен ақырсыз туындылар.
- Дифференциалдық геометриялық мағынасы.
- Функциялар дифференциалдарының негізгі формулалары.
ІІІ. Қорытынды
IV. Пайдаланылан әдебиеттер
Кіріспе
Түзудің бойындағы белгілі бір кесіндінің бүкіл бойы қандай да болса бір затпен толтырылған болсын. Бұндай материялық кесінді үшін ені мен жуандығы еске алынбаған стерженьді аламыз. Егер берілген кесіндінің, ұзындықтары бірдей, кез келген екі бөлігінің массалары тең болса, ол кесіндінің массасын бір текті дейді.
Бізге [a, b] сегментінде анықталған y=f(x) функциясы берілсін. Анықталу облысының кез келген нүктесіндегі туындысы туралы сөз қылғанда шеттік нүктелердегі туындылар туралы мәселе де қамтылады. Басқаша айтқанда:
біріншіден,
егер, y=f(x) функциясының [a, b] сегментінің сол жақ шетіндегі туындысы туралы сөз болып отырған болса, онда
 нольге тек оң жақтан ғана ұмтылғандағы
нольге тек оң жақтан ғана ұмтылғандағы
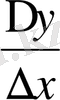 қатынасының шегін табу керек.
қатынасының шегін табу керек.
Ақырлы туындыны геометриялық тұрғыдан қарағанда жанаманың бұрыштық коэффициенті деп түсінетініміз бұрын айтылған. Ақырсыз туындының геометриялық мағынасын да дәл солай түсінеміз, бірақ соңғы жағдайда жанама ординаталар осіне параллель болады.
Функцияның ақырлы біржақтық туындыларының бар болуы мүмкін болса, сол сияқты, оның ақырсыз біржақтық туындылары да болуы мүмкін. Ақырсыз біржақтық туындылардың бар болуының аналитикалық сипаттамасы олардың таңбаларының әр түрлілігі болса, геометрияша сипаттамасы жалғыз ғана вертикаль жанаманың бар болатындығы.
- Туынды ұғымына келтіретін есептер.
1. Жылдамдық туралы есеп.
Материялық нүктенің бір қалыпты емес қозғалыс заңы
(1) арқылы берілген. Сонда (1) теңдеу қозғалатын материялық нүктенің жүрген жолы
 - ті жолды жүру үшін жұмсалған уақыт
- ті жолды жүру үшін жұмсалған уақыт
 нің функциясы түрінде анықтайды.
нің функциясы түрінде анықтайды.
t мезгілінен
 мезгіліне дейінгі мерзімді
мезгіліне дейінгі мерзімді
 деп, сол мерзім ішінде нүктеніңжүрген жолын
деп, сол мерзім ішінде нүктеніңжүрген жолын
 деп белгілейміз. Сонда
деп белгілейміз. Сонда
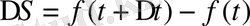
Онда
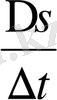 қатынасы нүктенің t мен
қатынасы нүктенің t мен
 мезгілі арасында өткен мерзімдегі орта жылдамдығы деп аталады.
мезгілі арасында өткен мерзімдегі орта жылдамдығы деп аталады.
Кез келген t мезгіліндегі жылдамдақ
 деп орта жылдамдықтың
деп орта жылдамдықтың
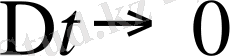 шегін айтады, яғни
шегін айтады, яғни
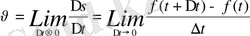
Сызықтық тығыздық туралы есеп.
Түзудің бойындағы белгілі бір кесіндінің бүкіл бойы қандай да болса бір затпен толтырылған болсын. Бұндай материялық кесінді үшін ені мен жуандығы еске алынбаған стерженьді аламыз. Егер берілген кесіндінің, ұзындықтары бірдей, кез келген екі бөлігінің массалары тең болса, ол кесіндінің массасын бір текті дейді. Берілген материялық кесіндінің ұзындық бірлігіне тиесілі масса
 болады. Осы
болады. Осы
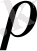 шамасы материялық кесіндінің сызықтық тығыздығы деп аталады. Нүктедегі сызықтық тығыздық ұғымын енгізу үшін ұзындығы
шамасы материялық кесіндінің сызықтық тығыздығы деп аталады. Нүктедегі сызықтық тығыздық ұғымын енгізу үшін ұзындығы
 ге тең берілген материялық кесіндінің бір шетін координата системасының бас нүктесі деп алсақ, екінші шетінің абсциссасы
ге тең берілген материялық кесіндінің бір шетін координата системасының бас нүктесі деп алсақ, екінші шетінің абсциссасы
 ге тең болады.
ге тең болады.
Берілген материялық кесінді
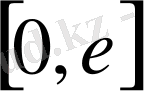 дің кез келген бөлігі
дің кез келген бөлігі
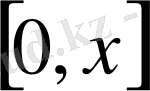 тің бойына орналастырылған заттың массасы
тің бойына орналастырылған заттың массасы

 тің қандайда бір функциясы болады, яғни
тің қандайда бір функциясы болады, яғни
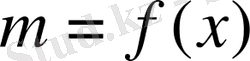 .
.
Ұзындығы
 ке тең
ке тең
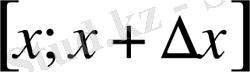 бөлігінің массасы
бөлігінің массасы
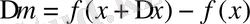 болады
болады
Сонда
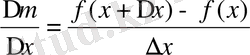
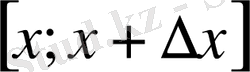 бөлігінің орта сызықтық тығыздығы деп аталады.
бөлігінің орта сызықтық тығыздығы деп аталады.
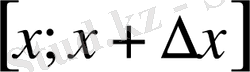 бөлігіндегі орташа сызықтың тығыздықтың
бөлігіндегі орташа сызықтың тығыздықтың
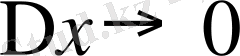 дағы шегі, яғни
дағы шегі, яғни
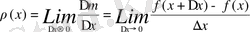
шамасы
 нүктесінің өте жақын қасындағы сызықтың тығыздық үшін алынады немесе материялық кесіндінің х нүктесіндегі сызықтың тығыздығы деп аталады.
нүктесінің өте жақын қасындағы сызықтың тығыздық үшін алынады немесе материялық кесіндінің х нүктесіндегі сызықтың тығыздығы деп аталады.
Жанама туралы есеп
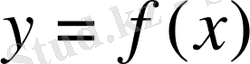 функцияның графигі берілген болсын.
функцияның графигі берілген болсын.
Берілген
 нүктесі арқылы жанама жүргізілсін. Ізделіп отырған жанаманың өтетін нүктесі
нүктесі арқылы жанама жүргізілсін. Ізделіп отырған жанаманың өтетін нүктесі
 белгілі болғандықтан, есепті шешу үшін жанаманың бұрыштық коэффициентін, яғни жанаманың абсциссалар өсінің оң бағытымен жасайтын бұрышы
белгілі болғандықтан, есепті шешу үшін жанаманың бұрыштық коэффициентін, яғни жанаманың абсциссалар өсінің оң бағытымен жасайтын бұрышы
 үшін
үшін
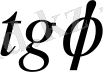 -ді яғни бұрыштық коэффициентті тапсақ жеткілікті. Ол үшін х ке аргумент өсімшесін береміз, сонда, функцияда өсімше алады, ол нүктені
-ді яғни бұрыштық коэффициентті тапсақ жеткілікті. Ол үшін х ке аргумент өсімшесін береміз, сонда, функцияда өсімше алады, ол нүктені
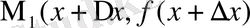 деп белгілейік.
деп белгілейік.
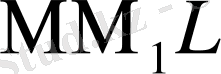 дің бұрыштың коэффициенті
дің бұрыштың коэффициенті
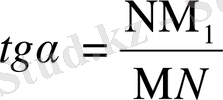
Ендеше
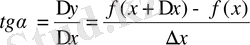
Қисықтың берілген М нүктесінен өтетін жанама
 -нің бұрыштың коэффициенті қиюшы
-нің бұрыштың коэффициенті қиюшы
 -дің
-дің
 нүктесі қисықтың бойымен қозғала М нүктесіне ұмтылғандағы шегі
нүктесі қисықтың бойымен қозғала М нүктесіне ұмтылғандағы шегі
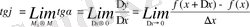
2)
анықтама
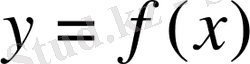 қисық сызығының берілен М нүктесіндегі жанамасы деп сол нүкте арқылы жүргізілген қиюшы
қисық сызығының берілен М нүктесіндегі жанамасы деп сол нүкте арқылы жүргізілген қиюшы
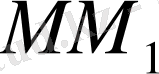 дің нүкте
дің нүкте
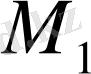 қиысықтың бойымен М нүктесімен беттесуге ұмтылғандағы шектік жағдайы МТ -ні айтады. Яғни хорда (керме)
қиысықтың бойымен М нүктесімен беттесуге ұмтылғандағы шектік жағдайы МТ -ні айтады. Яғни хорда (керме)
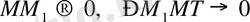
2. Туындының анықтамасы
Қандай да болса бір
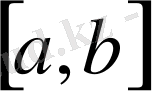 сегментінде анықталған функция
сегментінде анықталған функция
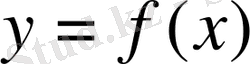 берілген.
берілген.
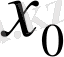 деп х тің
деп х тің
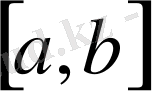 сегментіндегі бір нүктесін белгілейік. х ке
сегментіндегі бір нүктесін белгілейік. х ке
 өсімшесін берсек, оған сәйкес
өсімшесін берсек, оған сәйкес
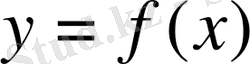 функциясы да жаңа мән қабылдайды, ол
функциясы да жаңа мән қабылдайды, ол
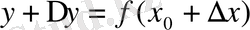
Сонда функция өсімшесі
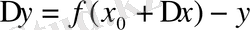 немесе
немесе
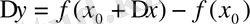 .
.
Функция өсімшесінің аргумент өсімшесіне қатынасын табамыз.
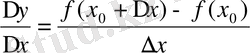
Егер тәуелсіз айнымалыныңөсімшесі
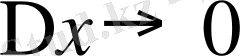 да функция өсімшесінің өзінің пайда болуына себепші болған тәуелсіз айнымалының өсімшесіне қатынасының шегі бар болса, яғни
да функция өсімшесінің өзінің пайда болуына себепші болған тәуелсіз айнымалының өсімшесіне қатынасының шегі бар болса, яғни
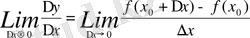
бар болса, бұл шек
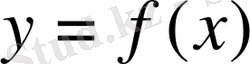 функциясының тәуелсіз айнымалы х бойынша алынған
функциясының тәуелсіз айнымалы х бойынша алынған
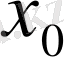 нүктесіндегі туындысы деп аталады. Туындының белгіленуі :
нүктесіндегі туындысы деп аталады. Туындының белгіленуі :
1) Лейбницше
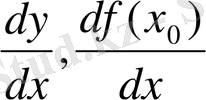
2) Логранж :
 немесе
немесе
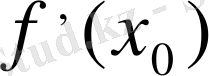
3) Коши:
 немесе
немесе
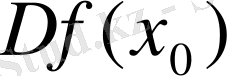
Егер
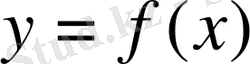 функциясының
функциясының
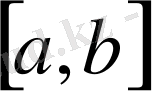 сегментінің әрбір х нүктесінде туындысы
сегментінің әрбір х нүктесінде туындысы
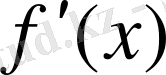 бар болса, ол
бар болса, ол
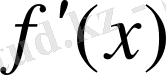 -тің өзі де х-тің сол
-тің өзі де х-тің сол
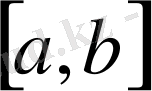 сегментінде анықталған функциясы болады.
сегментінде анықталған функциясы болады.
Берілген
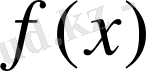 функциясының туындысы
функциясының туындысы
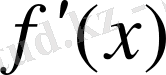 -ті іздеп табу амалы ол функцияны дифференциялдау деп аталады. Дифференциялдау ережелері мен туындылардың қасиеттері туралы ілім дифференциялдық есептеу деп аталады.
-ті іздеп табу амалы ол функцияны дифференциялдау деп аталады. Дифференциялдау ережелері мен туындылардың қасиеттері туралы ілім дифференциялдық есептеу деп аталады.
3. Туындының геометриялық және механикалық мағынасы
Берілген қисықтың бойында жатқан нүкте арқылы жанама жүргізу туралы есепті қарастырғанда
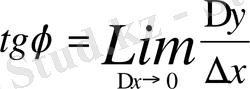 деген қорытындыға келгенбіз . Осы формула бойынша туындыға геометриялық мағына беруге болады:
деген қорытындыға келгенбіз . Осы формула бойынша туындыға геометриялық мағына беруге болады:
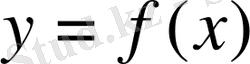 қисығының абщиссасы х-ке тең нүктесі арқылы жүргізілген жанаманың бұрыштық коэффициенті
қисығының абщиссасы х-ке тең нүктесі арқылы жүргізілген жанаманың бұрыштық коэффициенті
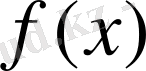 функциясының туындысы
функциясының туындысы
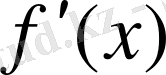 -ке тең болады.
-ке тең болады.
Қозғалыстағы материялық нүктенің лездік жылдамдығы туралы есепте оның
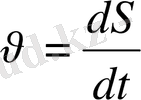 формуласы арқылы анықталатынын білгенбіз. Қозғалыстағы нүктенің жылдамдығы оның жүрген жолы S- тен уақыт t бойыншаа алынған туындысы болады.
формуласы арқылы анықталатынын білгенбіз. Қозғалыстағы нүктенің жылдамдығы оның жүрген жолы S- тен уақыт t бойыншаа алынған туындысы болады.
4. Туындысы болатын функцияның үзіліссіздігі.
Егер
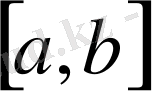 сегментінде анықталған
сегментінде анықталған
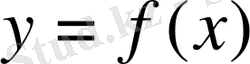 функциясының ол сегменттің белгілі бір нүктесінде туындысы болса, ол функция сол нұктеде үзіліссіз болады.
функциясының ол сегменттің белгілі бір нүктесінде туындысы болса, ол функция сол нұктеде үзіліссіз болады.
Теорема
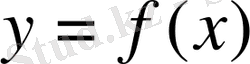 функциясы
функциясы
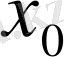 нүктесінде үзіліссіз болу үшін ол функцияның сол нүктеде ақырлы туындысы болуы жеткілікті .
нүктесінде үзіліссіз болу үшін ол функцияның сол нүктеде ақырлы туындысы болуы жеткілікті .
Д/У.
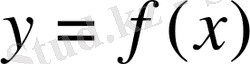 функциясының
функциясының
 нүктесінде ақырлы туындысы бар деп ұйғарайық
,
яғни
нүктесінде ақырлы туындысы бар деп ұйғарайық
,
яғни
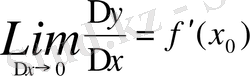 ақырлы шама дейік.
ақырлы шама дейік.
Мұндағы
 -аргумент өсімшесі, немесе ол
-аргумент өсімшесі, немесе ол
 ал
ал
 осы аргумент. өсімшесіне сәйкес функция өсімшесі. Функция туындысының анықтамасына сәйкес
осы аргумент. өсімшесіне сәйкес функция өсімшесі. Функция туындысының анықтамасына сәйкес
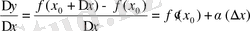 (2)
(2)
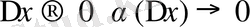
(2) формуладан
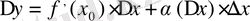 (3)
(3)
формуласы шығады (
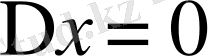 да
да
 деп ұйғарамыз)
деп ұйғарамыз)
Бұдан
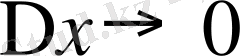 да
да
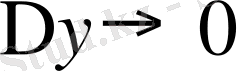 , яғни
, яғни
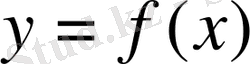 функциясы
функциясы
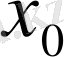 нүктесінде үзіліссіз.
нүктесінде үзіліссіз.
- Бір жақтық туындылар.
Бізге [a, b] сегментінде анықталған y=f(x) функциясы берілсін. Анықталу облысының кез келген нүктесіндегі туындысы туралы сөз қылғанда шеттік нүктелердегі туындылар туралы мәселе де қамтылады. Басқаша айтқанда:
біріншіден,
егер, y=f(x) функциясының [a, b] сегментінің сол жақ шетіндегі туындысы туралы сөз болып отырған болса, онда
 нольге тек оң жақтан ғана ұмтылғандағы
нольге тек оң жақтан ғана ұмтылғандағы
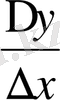 қатынасының шегін табу керек. Бұл жағдайда ізделетін туындыны
оң жақтық туынды
деп атайды да (1-сурет) былай белгілейді:
қатынасының шегін табу керек. Бұл жағдайда ізделетін туындыны
оң жақтық туынды
деп атайды да (1-сурет) былай белгілейді:
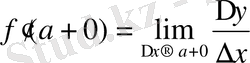 .
.

(1-сурет)
Екіншіден,
сол функцияның [a, b] сегментінің оң жақ шетіндегі туындысын есептеп табу керек болса, онда
 нольге тек сол жақтан ғана ұмтылғандаы
нольге тек сол жақтан ғана ұмтылғандаы
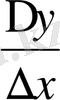 қатынасының шегін табу керек болады, бұл жағдайда сол жақтық туынды (76-чертеж) туралы айтылады да, ол туындыны былай белгілейді:
қатынасының шегін табу керек болады, бұл жағдайда сол жақтық туынды (76-чертеж) туралы айтылады да, ол туындыны былай белгілейді:
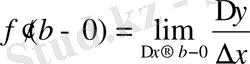

2-сурет
Бірақ кейде [a, b] сегментінің қандай да болса бір ішкі
 [a, b] нүктесінде
[a, b] нүктесінде
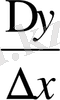 қатынасының шегі
қатынасының шегі
 нольге
нольге
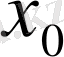 нүктесінің не тек оң жағынан, не тек сол жағынан ұмтылғанда ғана бар болуы, сонымен бірге ол шектердің екеуі де бар болған жағдайда олар өзара тең болмауы мүмкін. Бұл жағдайда ол шектерді
бір жақтық туындылар
деп атайды. Берілген y=f(x) функциясының өзінің анықталу облысының ішкі нүктесі
нүктесінің не тек оң жағынан, не тек сол жағынан ұмтылғанда ғана бар болуы, сонымен бірге ол шектердің екеуі де бар болған жағдайда олар өзара тең болмауы мүмкін. Бұл жағдайда ол шектерді
бір жақтық туындылар
деп атайды. Берілген y=f(x) функциясының өзінің анықталу облысының ішкі нүктесі
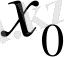 -де бір жақтық туындылары бар болуының геометриялық мағынасы сол
-де бір жақтық туындылары бар болуының геометриялық мағынасы сол
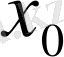 нүктесінде біржақтық жанамалардың бар болуы және олардың бір бірімен
нүктесінде біржақтық жанамалардың бар болуы және олардың бір бірімен
 нүктесіндегі белгілі бұрыш жасауында.
нүктесіндегі белгілі бұрыш жасауында.

3-сурет
Ақырсыз туындылар .
Қандай да болсын бір [a, b] сегментінде берілген функция y=f(x) үшін
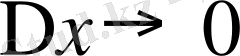 жағдайда
жағдайда
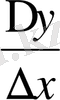 қатынасы не + ∞ -ке, не - ∞ ке, ұмтылса, бұл символды ақырсыз туынды деп атайды.
қатынасы не + ∞ -ке, не - ∞ ке, ұмтылса, бұл символды ақырсыз туынды деп атайды.
Ақырлы туындыны геометриялық тұрғыдан қарағанда жанаманың бұрыштық коэффициенті деп түсінетініміз бұрын айтылған. Ақырсыз туындының геометриялық мағынасын да дәл солай түсінеміз, бірақ соңғы жағдайда жанама ординаталар осіне параллель болады. (3, 4-сурет)
Функцияның ақырлы біржақтық туындыларының бар болуы мүмкін болса, сол сияқты, оның ақырсыз біржақтық туындылары да болуы мүмкін. Ақырсыз біржақтық туындылардың бар болуының аналитикалық сипаттамасы олардың таңбаларының әр түрлілігі болса, геометрияша сипаттамасы жалғыз ғана вертикаль жанаманың бар болатындығы.
4-сурет. 5-сурет.
6-сурет 7-сурет.
Егер
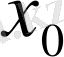 -нүктесінде функцияның ақырлы туындысы болса, ол функцияның сол нүктеде үзіліссіз болатындығы бұдан бұрын айтылған болатын. Ал, егер
-нүктесінде функцияның ақырлы туындысы болса, ол функцияның сол нүктеде үзіліссіз болатындығы бұдан бұрын айтылған болатын. Ал, егер
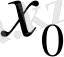 0 нүктесінде функцияның ақырсыз туындысы болса, оның осы нүктеде үзіліссіз болуы міндетті емес. Бұл пікірдің дұрыстығын мына мысалдан да көруге болады:
0 нүктесінде функцияның ақырсыз туындысы болса, оның осы нүктеде үзіліссіз болуы міндетті емес. Бұл пікірдің дұрыстығын мына мысалдан да көруге болады:
Мына функцияны алалық:
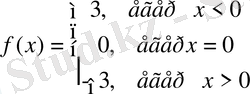 ,
,
 делік (8-чертеж) .
делік (8-чертеж) .
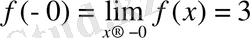 және
және
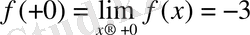 Бұл теңдіктерден функциямыз
Бұл теңдіктерден функциямыз
 нүктесінде ақырлы секірмелі болатынын көреміз.
нүктесінде ақырлы секірмелі болатынын көреміз.

8-сурет.
Енді бұл функцияның
 нүктесіндегі туындысын табалық. .
нүктесіндегі туындысын табалық. .
Функцияның берілу шарттарына қарағанда
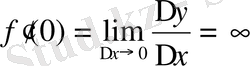
болады.
Демек, f(x) функциясы
 нүктесінде ақырсыз туындылы функция болады; сонымен бірге ол нукте f(x) үшін үзіліс нүктесі. Сөйтіп, бұл мысалда жоғарыда айтылған пікіріміздің дұрыстығы айқын көрінді.
нүктесінде ақырсыз туындылы функция болады; сонымен бірге ол нукте f(x) үшін үзіліс нүктесі. Сөйтіп, бұл мысалда жоғарыда айтылған пікіріміздің дұрыстығы айқын көрінді.
Бірнеше мысалдар тексерелік.
1.
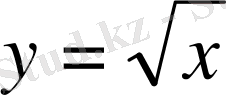 функциясының
функциясының
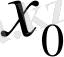 нүктесіндегі туындыcын есептеп шығару керек (9-сурет) .
нүктесіндегі туындыcын есептеп шығару керек (9-сурет) .
Шешуі:
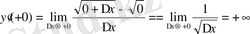

Демек берілген функцияның
 нүктесінде тек оң жақтық туындысы ғана бар және ол туынды +∞-ке тең.
нүктесінде тек оң жақтық туындысы ғана бар және ол туынды +∞-ке тең.
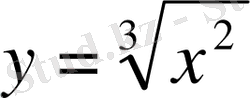 9-сурет 10-сурет
9-сурет 10-сурет

2.
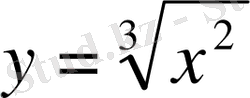 функциясының
функциясының
 нүктесіндегі туындысын табу керек
нүктесіндегі туындысын табу керек
10-сурет.
Шешу:
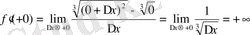
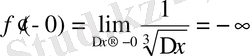
Демек,
 нүктесінде бұл функцияның біржақтық ақырсыз туындылары бар болып шықты.
нүктесінде бұл функцияның біржақтық ақырсыз туындылары бар болып шықты.
3.
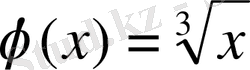 функциясының
функциясының
 нүктесіндегі туындысын есептеп шығару керек (11-сурет) .
нүктесіндегі туындысын есептеп шығару керек (11-сурет) .
Шешу:
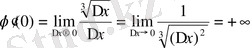
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz