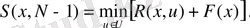Дискретті жүйелерде тиімді басқаруды синтездеу: Р. Беллманның динамикалық программалау әдісі


ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ және ҒЫЛЫМ МИНИСТРЛІГІ
Қ. И. Сәтбаев атындағы Қазақ Ұлттық Техникалық Университеті
Автоматика және телемеханика кафедрасы
РЕФЕРАТ
Тақырыбы: Р. Беллманның динамикалық программалау әдісімен дискретті жүйелерде тиімді басқаруды синтездеу
МАЗМҰНЫ
Кіріспе 3
Көпсатылы басқару процесі 4
Тиімді басқару есебі 5
Қарапайым келіс 5
Тиімділік принципі 6
Динамикалық программалау әдісі 7
Қадамды процедура 7
Тура процедура 8
Талқылау 9
Қорытынды 11
Қолданылған әдебиет 12
КІРІСПЕ
Динамикалық программалау әдісі - қазіргі заманғы басқару теориясының дәрменді және кең тараған математикалық әдістерінің бірі, ол 50-жылдардың аяғында американ математигі Р. Беллманмен ұсынылып жедел кең таралды. Көп ұзамай, динамикалық программалау әдісі аналитикалық механикада (үздіксіз уақытты жүйелер үшін) Гамильтон-Якоби классикалық әдісімен және Вальданың тізбектелген анализімен (дискретті уақытты жүйелер үшін), байланысты екені анықталды. Бірақ та динамикалық программалау әдісі туралы Беллманмен берілген аса жалпылама және тиянақты тұжырымдама, және осыған қоса экономика, экология және басқа білім облыстарында шешім қабылдау туралы теорияда әртүрлі мәселелеріне әдістің көптеген қосымшалары, осы әдістің басқарылатын процестер теориясында маңызды құралдардын бірі болып тіркелуіне әсер етті.
КӨПСАТЫЛЫ БАСҚАРУ ПРОЦЕСІ
Әр уақыт мезетінде n-өлшемді және
 элементтері бар
элементтері бар
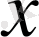 векторымен сипатталынатын басқарылатын жүйені қарастырайық. t уақыты дискретті өзгереді және тұтас санды мәндерді қабылдайды 0, 1, . . . деп қарастырайық. Оосылайша, экономикадағы және экологиядағы процестер үшін дискретті уақыт мәніне күндер, айлар және жылдар жауап береді, ал электронды құрылғылардағы процестер үшін көршілес дискретті уақыт моменттері арасныдағы аралық құрылғылардың қосылу уақытына тең. Әр қадамда жүйеге m-өлшемді және u
1
, …, u
m
-элементтері бар u-басқару векторы арқылы басқарулық әсер етсің деп ұйғарайық. Осылайша, t-уақыттың әр мезетінде жүйенің қалпы
векторымен сипатталынатын басқарылатын жүйені қарастырайық. t уақыты дискретті өзгереді және тұтас санды мәндерді қабылдайды 0, 1, . . . деп қарастырайық. Оосылайша, экономикадағы және экологиядағы процестер үшін дискретті уақыт мәніне күндер, айлар және жылдар жауап береді, ал электронды құрылғылардағы процестер үшін көршілес дискретті уақыт моменттері арасныдағы аралық құрылғылардың қосылу уақытына тең. Әр қадамда жүйеге m-өлшемді және u
1
, …, u
m
-элементтері бар u-басқару векторы арқылы басқарулық әсер етсің деп ұйғарайық. Осылайша, t-уақыттың әр мезетінде жүйенің қалпы
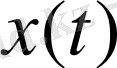 -векторымен, ал басқарулық әсері u(t) -векторымен сипатталынсын. Әдетте басқарудын таңдауына шенеулер қойылады, оларды жалпы түрде келесідей бейнелеуге болады
-векторымен, ал басқарулық әсері u(t) -векторымен сипатталынсын. Әдетте басқарудын таңдауына шенеулер қойылады, оларды жалпы түрде келесідей бейнелеуге болады
(1)
Мндағы U - n-өлшемді кеңітікте берілген жиын.
t моментінде таңдап алынған басқарудың әсерінен жүйе келесі уақыт моментінде жаңа күйге көшеді
(2)
Мұндағы
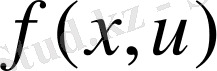 - қарастырылып отырған жүйенің динамикасын сипаттайтын n-өлшемді
- қарастырылып отырған жүйенің динамикасын сипаттайтын n-өлшемді
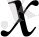 векторынан және m-өлшемді u векторынан n-өлшемді функция. Осы функция анықталған (берілген) деп ұйғарылады және қарастырылып отырған басқару процесінің қабылданған математикалық моделіне жауап береді.
векторынан және m-өлшемді u векторынан n-өлшемді функция. Осы функция анықталған (берілген) деп ұйғарылады және қарастырылып отырған басқару процесінің қабылданған математикалық моделіне жауап береді.
Жүйенің бастапқы күйін белгілейік
(3)
мұндағы
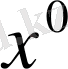 - берілген n-өлшемді вектор. Сонымен, көпсатылы басқару процесі (1) -(3) ара қатынастарымен сипатталынады. Нақты процесті есептеу процедурасы келесідей болады. Кез келген t момент кезінде жүйенің қалпы
- берілген n-өлшемді вектор. Сонымен, көпсатылы басқару процесі (1) -(3) ара қатынастарымен сипатталынады. Нақты процесті есептеу процедурасы келесідей болады. Кез келген t момент кезінде жүйенің қалпы
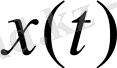 анықталған болсын. Сонда
анықталған болсын. Сонда
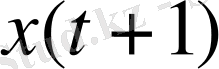 қалпын анықтау үшін екі операцияны орындау керек: 1) (1) шартты қанағаттандыратын мүмкін болатын
қалпын анықтау үшін екі операцияны орындау керек: 1) (1) шартты қанағаттандыратын мүмкін болатын
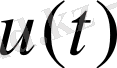 бақылауды таңдап алу; 2) (2) бойынша келесі уақыт мезетінде
бақылауды таңдап алу; 2) (2) бойынша келесі уақыт мезетінде
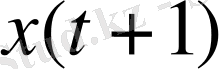 қалпын анықтау. Жүйенің бастапқы қалпы берілген болғандықтан, жоғарыда келтірілген процедураны барлық
қалпын анықтау. Жүйенің бастапқы қалпы берілген болғандықтан, жоғарыда келтірілген процедураны барлық
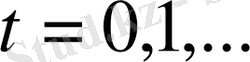 үшін тізбектеле орындауға болады. Қалыптардың
үшін тізбектеле орындауға болады. Қалыптардың
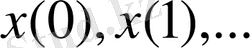 тізбегі жиі жүйенің траекториясы деп аталады.
тізбегі жиі жүйенің траекториясы деп аталады.
Әр қадамда бақылауда таңдау едәуір еркін екенің ескерейік. Ол еркіндік жоқ болып кетеді, егер бақылаудың мақсатын қайсыбір оптималдылық критериін минимизациялау немесе максимилизациялау талабы түрінде белгілесек.
ТИІМДІ БАСҚАРУ ЕСЕБІ
Басқару процесінің қайсыбір сапалық критериі (оптималдылық критериі) келесі түрде берілсін
(4)
Мұндағы
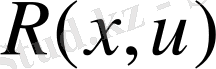 және
және
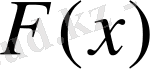 - өздернің аргументтерінің берілген скалярлық функциялар,
- өздернің аргументтерінің берілген скалярлық функциялар,
 - процестің аяқталу моменті,
- процестің аяқталу моменті,
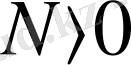 .
.
Динамикалық программалау есебі, (1) шенеулерді қанағаттандыратын, және белгілі бір траекторияға сәйкес келетін, ол
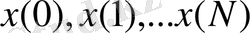 тізбегі, олардың жиынтығы (2), (3) процестер үшін (4) -критеридін минималды мәнің береді,
тізбегі, олардың жиынтығы (2), (3) процестер үшін (4) -критеридін минималды мәнің береді,
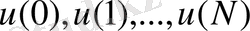 мүмкін болатын басқаруларды анықтау есебі түрінде тұжырымдалады.
мүмкін болатын басқаруларды анықтау есебі түрінде тұжырымдалады.
(4) -критериді минимизациялау әдетте, аз мөлшерде қаражаттарды, ресурстарды, энергияны, берілген мақсаттан немесе траекториядан ең аз ауытқып кетуді қамтамасыз ететін басқаруды таңдап алуда жауап береді. Сонымен қатар (4) түріндегі критериді максимизациялау есебі жиі қолданылады, мысалға өндірістің табысын немесе көлемін максимизациялау. Бірақ та, J критериін максимизациялау (-J) критериін минимизациялау балама келіп тұрғанын көруге болады. Сондықтан R және F функциялараның жай ғана таңбаларын ауыстыру критериді максимизациялау есебін оны минимизациялауға әкеледі. Ары қараай анықталу үшін (4) -критериді минимизациялау есебін қарастырамыз.
ҚАРАПАЙЫМ КЕЛІС
Алдымен қарапайым келісті қойылған оптималды басқару есебіне қарастырайық. Жүйенің қалпы келесі әр уақыт моментінде оның алдынғы уақыт моменті кезіндегі қалпы мен басқаруы арқылы (2) теңдіктің көмегімен бейнеленеді. Сонда осы теңдікті көп рет қолдана отырып, тек қана
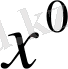 бастапқы қалпы арқылы жүйенің барлық уақыт моментінде қалпын және алдынғы моменттегі басқаруды көрсетуге болады. Нәтижесінде (4) критериден
бастапқы қалпы арқылы жүйенің барлық уақыт моментінде қалпын және алдынғы моменттегі басқаруды көрсетуге болады. Нәтижесінде (4) критериден
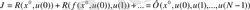
аламыз.
Мұндағы Ф - қайсыбір үлкен, бірақ, былай айтқанда, өз аргументтері анықталған функция. Осылайша, қойылған оптималды басқару есебі
 векторларынан Ф фунуциясын минимизациялау есебіне түйісті. N үлкен кезде (әдетте N-үлкен процестер қызығушылық көрсетеді) көп санды айнымалылары бар функцияны минимизациялау есебі едәуір күшті компьютерлерді қоллданғанымен үлкен қиындық көрсетеді. Тағы да бір қиыншылықтар, ол
векторларынан Ф фунуциясын минимизациялау есебіне түйісті. N үлкен кезде (әдетте N-үлкен процестер қызығушылық көрсетеді) көп санды айнымалылары бар функцияны минимизациялау есебі едәуір күшті компьютерлерді қоллданғанымен үлкен қиындық көрсетеді. Тағы да бір қиыншылықтар, ол
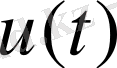 айнымалылары (1) шенеулерді қанағаттандыруы тиіс.
айнымалылары (1) шенеулерді қанағаттандыруы тиіс.
Осы қойылған мәселеге принципиалды басқа келісті динамикалық программалау әдісі береді.
ТИІМДІЛІК ПРИНЦИПІ
Р. Беллманмен тұжырымдалған оптималдылық принципі: оптималды процесстің кез келген нүктесінен процестің аяғына дейінгі кесіндісі осы нүктеден басталып өзі оптималды процесс болып келеді.
Оптималдылық принципі қастан жеңіл дәлелденеді.
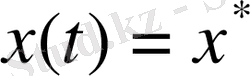 -оптималды траекторияның кез келген нүктесі болсын, сонда жүйенің қалпы оптималды процесс бойымен t моментінде, 0 ‹ t ‹ N. Бастапқы шарт
-оптималды траекторияның кез келген нүктесі болсын, сонда жүйенің қалпы оптималды процесс бойымен t моментінде, 0 ‹ t ‹ N. Бастапқы шарт
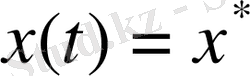 кезінде осы процес t моментінен N моментіне дейінгі кесіндісі (1), (2) жүйелер үшін сапалық критериінің мәнісінде оптималды процесс емес деп болжайық
кезінде осы процес t моментінен N моментіне дейінгі кесіндісі (1), (2) жүйелер үшін сапалық критериінің мәнісінде оптималды процесс емес деп болжайық
. (5)
Ендеше, мүмкін болатын
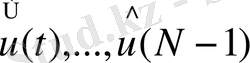 басқару және оған сәйкес келетін
басқару және оған сәйкес келетін
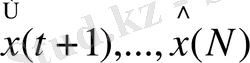 траектория бар, осылар үшін
траектория бар, осылар үшін
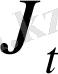 критериі (5) -теңдеуден, бастапқы оптималды шарттан қарағанда, кіші мәнің қабылдайды. 1 суретте бастапқы оптималды траектория
критериі (5) -теңдеуден, бастапқы оптималды шарттан қарағанда, кіші мәнің қабылдайды. 1 суретте бастапқы оптималды траектория
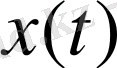 қызыл сызықпен, ал
қызыл сызықпен, ал
 - траекториясы көк сызықпен көрсетілген. Бастапқы оптималды процеспен
- траекториясы көк сызықпен көрсетілген. Бастапқы оптималды процеспен
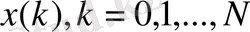 қатар, екі бөліктен тұратын процесті қарастырайық:
қатар, екі бөліктен тұратын процесті қарастырайық:
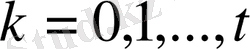 болған кездегі бастапқы процесс
болған кездегі бастапқы процесс
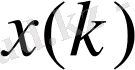 және
және
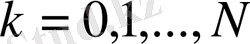 болған кездегі жақсартылған
болған кездегі жақсартылған
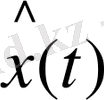 процесс. Осы құрамдас процесс үшін (4) алынған J критериі, бастапқы процеске қарағанда, кіші мәнге ие болады, өйткені (4) бойынша t-қосындысы құрамдас пароцесс және бастапқы процесс үшін сол беті қалады, ал қалған қосылғыштардын (5) бойынша
процесс. Осы құрамдас процесс үшін (4) алынған J критериі, бастапқы процеске қарағанда, кіші мәнге ие болады, өйткені (4) бойынша t-қосындысы құрамдас пароцесс және бастапқы процесс үшін сол беті қалады, ал қалған қосылғыштардын (5) бойынша
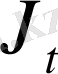 -тең жиынтығы, бастпақы процеспен салыстырғанда кемиді.
-тең жиынтығы, бастпақы процеспен салыстырғанда кемиді.
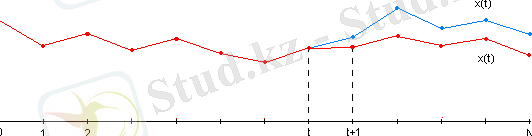
1 сурет. Басқарылатын процестің траекториялары
Жасалынған тұжырым процестің оптималды еместінтігін анықтайды, ал бұл жасалынған болжауға кері келеді.
Осылайша, оптималдылық принципі дәлелденді. Дәлелдеудің осындай қарапайымдылығы әдістің травиалдылығы туралы ойға әкеледі. Бірақ та, ол олай емес: оптималдылық принципі (4) түріндегі оптималдылық критериінің аддитивтілігі болып келеді және аддитивтілік емес критерий кезінде орын алмайды, мысалға (4) түріндегі критеридін қайсыбір функциясы болған кезде.
ДИНАМИКАЛЫҚ ПРОГРАММАЛАУ ӘДІСІ
Булгілеу енгізейік:
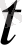 моментінде
моментінде
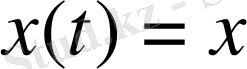 нүктесінен басталатын, оптималды процесс үшін (5) бойынша
нүктесінен басталатын, оптималды процесс үшін (5) бойынша
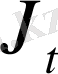 сапалық критериінің минималды мәні -
сапалық критериінің минималды мәні -
 . Бұл процесті екі бөліктен тұрады деп қарастыруға болады:
. Бұл процесті екі бөліктен тұрады деп қарастыруға болады:
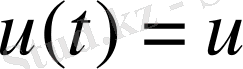 басқаруы таңдалып алынатын бірінші қадамнан, және қалған бөліктен (
басқаруы таңдалып алынатын бірінші қадамнан, және қалған бөліктен (
 моментінен процестің аяғына дейін) . Процестің бірінші бөлігінің сапа критериіне аманаты
моментінен процестің аяғына дейін) . Процестің бірінші бөлігінің сапа критериіне аманаты
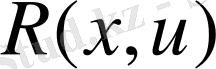 -тең, ал екінші бөліктің аманатын, оптималдылық принципіне сәйкес, жоғарыдағы енгізілген
-тең, ал екінші бөліктің аманатын, оптималдылық принципіне сәйкес, жоғарыдағы енгізілген
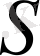 функциясы арқылы келесі түрде бейнелеуге болады
функциясы арқылы келесі түрде бейнелеуге болады
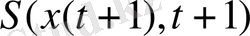 . Бірінші бөлікте басқарулық
. Бірінші бөлікте басқарулық
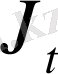 критериін минимизациялау шартынан таңдап алынатының ескере отырып, (1) шенеулегенде келесі теңдікті аламыз
критериін минимизациялау шартынан таңдап алынатының ескере отырып, (1) шенеулегенде келесі теңдікті аламыз
.
Осы жерде және ары қарай анық болу үшін,
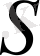 функциясы және (2), (4) енгізілген
функциясы және (2), (4) енгізілген
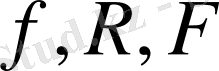 функциялары үздіксіз деп болжаймыз. Жоғарыда ылынған теңдікке (2) қоя отыра, динамикалық программалау әдісінің негізгі ара қатынасын аламыз
функциялары үздіксіз деп болжаймыз. Жоғарыда ылынған теңдікке (2) қоя отыра, динамикалық программалау әдісінің негізгі ара қатынасын аламыз
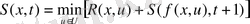
(6)
 моментінде басталатын оптималды процесс үшін, (5) оптималдылық критериі ақырлы бір қосылғышқа келеді. Сондықтан
моментінде басталатын оптималды процесс үшін, (5) оптималдылық критериі ақырлы бір қосылғышқа келеді. Сондықтан
(7)
шартын аламыз.
Бастапқы шарттын рөлін ойнайтын, (6) қатынасы және (7) шарты
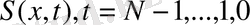 функциясын анықтауға, және оптималды басқару мен оптималды траекторияны есептеуге мүмкіндік береді. Бұл динамикалық программалаудың қадамды және тура процедураларын тізбектеле іске асыру арқылы нәтижеге жетеді.
функциясын анықтауға, және оптималды басқару мен оптималды траекторияны есептеуге мүмкіндік береді. Бұл динамикалық программалаудың қадамды және тура процедураларын тізбектеле іске асыру арқылы нәтижеге жетеді.
ҚАДАМДЫ ПРОЦЕДУРА
Қайсыбір аргумент бойынша функцияның минимумын есептегенде екі шама алынатының, ескерейік: минимум жеткендегі, минимум мәні және аргумент мәні. Бұл мән бір ғана емес болуы мүмкін, сол үшін оны
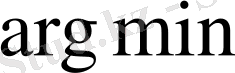 символымен белгілейміз.
символымен белгілейміз.
(6) өрнекте
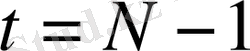 деп (7) шартты қолдана отырып, келесіні аламыз
деп (7) шартты қолдана отырып, келесіні аламыз
Осы минимумды есептей отыра
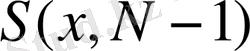 функциясын, және осы минимумды беретін
функциясын, және осы минимумды беретін
 - мәнің табамыз:
- мәнің табамыз:
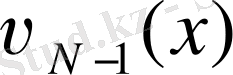 жазуы
жазуы
 мәні
мәні
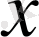 параметр ретінде тәуелді екенің көрсетеді.
параметр ретінде тәуелді екенің көрсетеді.
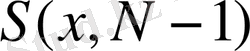 анықтай отыра және де
анықтай отыра және де
 деп белгілеп, (6) бойынша
деп белгілеп, (6) бойынша
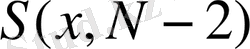 функциясын және оған сәйкес аргументтің мәнің
функциясын және оған сәйкес аргументтің мәнің
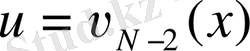 анықтаймыз. Осы процесті
анықтаймыз. Осы процесті
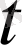 азаюына қарай жалғастыра берсек, (6) бойынша
азаюына қарай жалғастыра берсек, (6) бойынша
 кезінде
кезінде
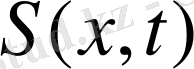 және
және
(8)
функцияларын аламыз.
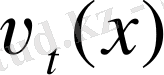 функциясы
функциясы
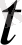 момент кезінде оптималды басқаруды анықтайды, егер жүйе
момент кезінде оптималды басқаруды анықтайды, егер жүйе
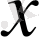 қалпында болса. Бұндай басқаруды беру формасы кері байланыс арқылы басқару деп аталады.
қалпында болса. Бұндай басқаруды беру формасы кері байланыс арқылы басқару деп аталады.
Осылайша, қадамды процедура барлық
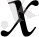 және
және
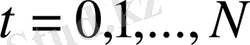 үшін
үшін
 ,
,
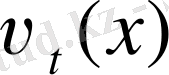 фунуцияларын анықтаудан тұрады.
фунуцияларын анықтаудан тұрады.
ТУРА ПРОЦЕДУРА
Бастапқы есепті шешу үшін қадамды процедураның нәтижесін қолданайық, ол дегеніміз (3) түріндегі бастапқы шарт берілген кездегі оптималды басқаруды және оптималды траекторияны тұрғызу үшін.
(8) бойынша
 және
және
 деп ұйғарып, бастапқы момент кезіндегі басқаруды табайық:
деп ұйғарып, бастапқы момент кезіндегі басқаруды табайық:
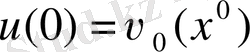 . Ары қарай (2) қатынастан
. Ары қарай (2) қатынастан
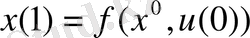 қалпын анықтайық. Осы процесті жалғастыра отыра,
қалпын анықтайық. Осы процесті жалғастыра отыра,
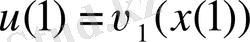 ,
,
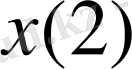 анықтайық және т. с. с. Жалпы түрде
анықтайық және т. с. с. Жалпы түрде
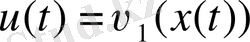
(9)
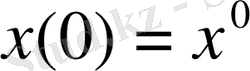
.
(9) қатынастар тура процедураны анықтайды, және оптималды басқару мен оптималды траекторияны толығымен есептеп шығаруға мүмкіндік береді. Осы траекторияға жауап беретін, оптималдылық критериінің минималды мәні
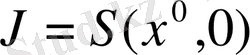 .
.
МЫСАЛ
Көрнекті мысал ретінде мал мен құс өсіретін ферманың оптималды жұмыс істеуі туралы модельді есепті қарастырайық.
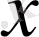 -белгілі бір уақыт аралығынын басында фермадағы малдын немесе құстын саны болсын. Осы шамадан
-белгілі бір уақыт аралығынын басында фермадағы малдын немесе құстын саны болсын. Осы шамадан
 малдар сатылуға кетеді, ал қалғаны көбеюге қалады, сол себептен олардын саны қарастырылып отырған аралықта
малдар сатылуға кетеді, ал қалғаны көбеюге қалады, сол себептен олардын саны қарастырылып отырған аралықта
 рет көбееді. (2) теңдік келесі түрге келеді
рет көбееді. (2) теңдік келесі түрге келеді
(10)
мұндағы q›1-тұрақты коэфициент,
 -басқару әсері (сатылуға кететін малдын мөлшері) . (1) түрдегі шенеу келесі түрде болады
-басқару әсері (сатылуға кететін малдын мөлшері) . (1) түрдегі шенеу келесі түрде болады
 .
.
Малды қарауға кеткен шығынды олардын қалған мөлшеріне пропорционал етіп алайық және олар
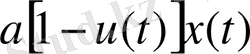 тең, мұндағы
тең, мұндағы
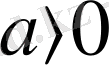 -тұрақты. Малды сатудан шыққан табысты
-тұрақты. Малды сатудан шыққан табысты
 деп есептейік, мұндағы
деп есептейік, мұндағы
 -бір малдын рыноктагы бағасы. Есепті уақыт бойынша N қадам ішінде ферманың табысын максимизациялау түрінде қойяық. Жоғарыда айтылып кеткендей, бұл есеп шығынды минимизацияуға балама келеді. (4) түрдегі оптималдылық критериі, жоғарыда айтылғандарды ескере отыра келесі түрге келеді
-бір малдын рыноктагы бағасы. Есепті уақыт бойынша N қадам ішінде ферманың табысын максимизациялау түрінде қойяық. Жоғарыда айтылып кеткендей, бұл есеп шығынды минимизацияуға балама келеді. (4) түрдегі оптималдылық критериі, жоғарыда айтылғандарды ескере отыра келесі түрге келеді
(11)
Ақырғы (11) теңдік (теріс таңбамен) процестін аяғында фермадағы малдын бағасын анықтайды. (10) мен (11) ескере отыра қарастырылып отырған есеп үшін (6) теңдікті құрастырайық
(12)
(7) шарт (11) ескере оытра келесі түрге келеді
(13)
Қиын емес анализ қадамды процедураны іске асыруға және (12), (13) есеп үшін
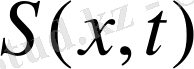 функцияларын және оған сәйкес
функцияларын және оған сәйкес
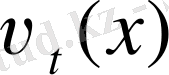 басқаруларды құруға мүмкіндік береді. Ақырлы нәтижелерді келтірейік:
басқаруларды құруға мүмкіндік береді. Ақырлы нәтижелерді келтірейік:
... жалғасы
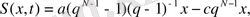
егер
(14)
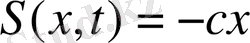
егер
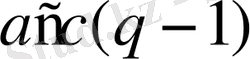
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz