Өндірістік және экономикалық процестерді модельдеу: сызықты программалау, графикалық әдіс және транспорт есебін потенциалдар әдісімен шешу


ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ
ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Қ. И. Сатпев атындағы ҚазҰТУ колледжі
КУРСТЫҚ ЖҰМЫС
Өндірістік және экономикалық процессті
модельдеу.
нұсқа.
Жазған:
Тексерген:
АЛМАТЫ 2009
Мазмұны
- К І Р І С П Е . . . 2
- СЫЗЫҚТЫ ПРОГРАММАЛАУ (СП) ЕСЕПТЕРДІҢ ШЕШУДІҢ ГРАФИКАЛЫҚ ӘДІСІ . . . 4
- ГРАФИКАЛЫҚ ӘДӘСТІҢ АЛГОРИТМІ . . . 5
- СЫЗЫҚТЫ ПРОГРАММАЛАУДЫҢ (СП) ТРАНСПОРТ ЕСЕБІН ПОТЕНЦИАЛДАР ӘДІСІМЕН ШЕШУ . . . 12
- БАҚЫЛАУ ЖҰМЫСЫН ШЕШУ . . . 17
- ҚОРЫТЫНДЫ . . . 24
- ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 25
I. КІРІСПЕ
Жүйелер теориясының әдістері экономикада, физикада, инженерлік қызметте, т. б. практикалық істерде пайда болатын есептерді шешуге бейімделген курс. Тиімді шешімді табуға арналған есептер оптимизациялық есептер деп аталады. Оптимал нәтиже бірден табылмайды, ол оптимизациялау процессі деп аталатын процестің нәтижесінен шығады. Оптимизациялық есептер деп аталады. Оптимал нәтиже бірден табылмайды, ол оптимизациялау процесі деп аталатын процестің нәтижесінен шығады. Оптимизациялау процесінде пайдаланатын әдістер оптимизациялау әдістері деген атқа ие болды.
Қарапайым жағдайларда біз бірден есептің шарттарын математика тілінде аударамыз да, оның матиматикалық тұжырымын аламыз. Бірақ та, іс жүзінде есепті формализациялау процесінің қиындықтары көп. Мысалы, цехта өңделген бұйымдарды, бұйымның әр түрін шығару жоспарының ең аз шығынымен орындалуы қамтамасыз етілетіндей әртүрлі типтегі құрал-жабдықтарға тиімді болу керек.
Есептің шығарылу процесі келесі этаптармен беріледі:
- Объектіні зерттеу. Бұл этапта, болып жатқан процестерді түсіну, қажетті параметрлерді (мысалы, әртүрлі және өзара алмастырылатын типтегі құралдар саны, оның әрбір бұйым түрін өңдеудегі өнімділігі, т. б. ) анықтау талап етіледі.
- Модельге сипаттама процесс сипаттамаларының арасындағы негізгі байланыстар мен тәелділіктерінің критерийі тұрғысынан қарағандағы мәтінін жазу.
- Математикалық модельдеу - модельді мәтіндік сипаттамасын математикалық тілге аудару. Барлық шарттар сәйкес шектеулер жүйесі түрінде жазылады ( теңдеу, теңсіздік ) . Бұл жүйенің кез келген шешімі үйлесімді шешім деп аталады. Критерии функция түрінде жазылады, оны әдетте мақсат функциясы деп атайды. Тиімдеу есебін шешу, әдетте, шектеулер жүйесінің шешімдер жағынан мақсат функциясына ең үлкен немесе ең кіші мәнін іздеу болып табылады.
- Есепті шешу әдісін таңдау. Есеп математикалық формада жазылғандықтан, оның нақты мазмұны бізді қызықтырмайды. Әртүрлі есептің формальді тұжырымдарының бірдей болуы мүмкін. Сондықтан, шешу әдісін таңдаған кезде есептің мазмұнына емес, алынған математикалық құрымына назар аударамыз. Кейбір есептердің ерекшеліктеріне байланысты белгілі әдістерді модификациялау немесе жаңа әдіс ойлап табу қажет болуы мүмкін.
- Есепті ЭЕМ - да шешу үшін программа жазу немесе таңдау. Іс жүзінде айнымалылар санының және олардың арасындағы байланысты есептер тек ЭЕМ көмегімен шығарылады.
- Есепті ЭЕМ - де шешу.
- Алынған нәтижені сараптау. Алынған шешімді сараптаудың екі түрі болуы мүмкін: формальді (математикалық), яғни құрылған математикалық модельдің шешімінің дұрыстығы (дұрыс болмаған жағдайда программа, берілген мәліметтер, т. б. ) яғни алынған шешімнің модельденген объектіге сәйкес болуы.
Осындай сараптаудың нәтижесінде модельге өзгертулер немесе түсініктемелер енгізілуі мүмкін, содан соң өңдеу процесі толық қайталанылады. Егер, таңдалған критерий бойынша модель объектінің қызметін жеткілікті дәлдікпен сипаттайтын болса, онда модель құрылған және аяқталған болып саналады. Тек осыдан соң ғана модельді есептеулер үшін пайдалануға болады. Математикалық программалау дегеніміз - экстремальды есептерді зерттейтін және олардың шешу әдістерін құрумен айналысатын математикалық пән. Жалпы түрде экстремальді есептердің математикалық қойылуы q i (x 1 …, x n ) ≤b i (i=1, m) шектеулеріне f=(x 1 …, x n ) мақсатты функциясының ең үлкен немесе ең кіші мәндерін анықтаудан тұрады, бұл жерде f және q i берілген функциялар, ал b i - кейбір нақты сандар q i және f функцияларының қасиеттеріне байланысты пограммалау, есептердің белгілі бір класстарының шешу әдістерін зертеу және құрумен айналысатын жеке пәндер болы қарастырылуы мүмкін. Ең алдымен математикалық программалау есептері сызықты және сызықты емес болып бөлінеді. Сонымен қатар, егер f және q i сызықты болса, сәйкес есепте сызықты программалау есебі болып табылаы. Егер, көрсетілген функциялардың біреуі сызықты емес болса, онда сәйкес есепте сызықты емес программалау есебі болып табылады. Математикалық программалаудың ең көп зерттегені сызықты программалау болып табылады. Сызықты программалау есептерін шешу үшін бірқатар ұтымды әдістер, алгоритмдер және программалар жасалған. Сызықты емес программалау есептерінің ішінде ең терең зерттелгені дөңес бағдарламалау есептері. Бұл есептердің шешілу нәтижесінде дөңес тұйық жиында берілген функцияның ең кіші дөңесті (немесе ең үлкен ойыстығы) анықталады. Бүтін санды программалау, параметрлері және бөлшек сызықты программалау есептері программалаудың жеке бір кластары болып табылады. Бүтін санды программалау есептерінеде белгісіздер тек бүтін мәндер ғана қабылдай алады.
II. СЫЗЫҚТЫ ПРОГРАММАЛАУ (СП) ЕСЕПТЕРДІҢ ШЕШУДІҢ ГРАФИКАЛЫҚ ӘДІСІ.
Графикалық әдіс n=2 немесе n=3 болғандағы СП есептеріне және сонымен қатар n-m=2 қатынасымен байланысқан n белгісіз, m сызықты тәуелсіз теңдеулерден тұратын шектеулер жүйесі бар СП есептеріне қолданылады. СП есебінің екі өлшемді кеңістіктегі есебі ең көрнекті болып табылады. Осы жағдай үшін есеп құрастырайық:
L(x) =c 1 x 1 +c 2 x 2 (1)
мақсат функциясының экстремумын келесі шектеулерде табу керек:

 (2)
(2)
x 1m ≥ 0, x 2m ≥0 (3)
III ГРАФИКАЛЫҚ ӘДІСТІҢ АЛГОРИТМІ
- Барлық нүктелері алғашқы шектеулер жүйесін (3) -(2) қанағаттандыратын үлесімді шешімдер көпбұрышын (шектелмеген аймақ болуда мүмкін) тұрғызамыз. Бұл үшін (3) және (2) теңсіздіктер жүйесі үшін сәйкес шекаралық түзулердің теңдеулерін жазамыз және оларды х10х2жазықтығына жүргіземіз. Әрбір шекаралық түзу жазықтықты екі жарты жазықтыққа бөледі. Шешімнің жарты жазықтығын анықтау үшін жазықтықтың кез келген нүктесінің кординатын сәйкес теңдікке қою керек. Егер бұл нүкте теңсіздікті қанағаттандырса, онда шешімнің жарты жазықтығы деп жазықтықтың нүктеде жатқан бөлігін алу керек.
Шешімнің жарты жазықтығын бағдаршалармен белгілейміз. Осы жолмен барлық теңсіздіктердің шешімдер аймағы құрылады және олардың ортақ бөлімі анықталады.
- (1) параллель түзулер тобына жататын L0- бастапқы түзуін және (1) сызықтық форманың өсу бағытын көрсететін градиент(с1с2) жүргіземіз.
- Бастапқы түзу L0- ді тірек жағдайға келгенше, яғни шешімдер көпбұрышы оның бір жағында жататындай және онымен ең аз дегенде бір ортақ нүктесі болатындай күйге келгенше өзіне - өзін параллель жылжытамыз. Сонда L0бастапқы түзуінің(с1с2) бағытында қабылдайтын бірінші тірек күйі Lmin, ал Lmax.
- Экстремум нүктелерінің координаттарын анықтаймыз, ол үшін қиылысу нәтижесінде осы нүктелер пайда болған шекаралық түзулердің теңдеуін бірге шешеміз және осы нүктелердегі мақсат функциясының мәнін есептейміз.
Ескерту: Тірек түзуі шешімдер көпбұрышының бір қырымен қабаттасып келген жағдайда мақсат функциясы бір мезгілде екі бұрыштық Х 1 0 және Х 2 0 нүктелерде экстрималдық мән қабылдайды. Бұл жағдайда тиімді жоспарлар жиыны туралы теорема негізінде (1) сызықты форма Х 1 0 және Х 2 0 нүктелерінің дөңес комбинациялары болатын барлық нүктелерде, яғни
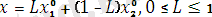
(4)
нүктелерінде бірдей экстремальды мәндер қабылдайды.
Бақылау мысалын шешу
L(x) =3x 1 + 2x 2 → экстр. (5)
Мақсат функциясының максимумы мен минимумы келесі шектеулерде табу керек:
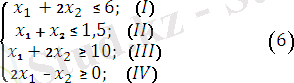
X
1

 0; X
2
≥0; (7)
0; X
2
≥0; (7)
Шешімдер көпбұрышын құрып шекаралық түзулердің теңдеулерін жазамыз. (бұл түзулердің теңдеуін құру ыңғайлы болу үшін, мүмкін болған жағдайда кесінді теңдеулер түрінде береміз, яғни х 1 /а+х 2 /b=1) :
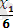
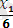 +
+
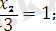
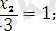 (I)
(I)
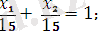
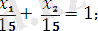 (II)
(II)
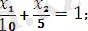
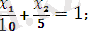 (III) (8)
(III) (8)
+
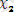
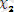 =0; (IV)
=0; (IV)
x 1 =0; x 2 =0; (9)
- Ox1осінде 6-ға, Ох2осінде (-3) - ке тең кесінді қиып түсіретін (I) шекаралық түзуді жүргізіп, шешімдер жарты жазықтығын анықтаймыз. Ол үшін О(0, 0) нүктесінің координаттарының сәйкес (I) теңсіздігіне қоямыз. Бұл теңсіздік дұрыс, сондықтан О(0, 0) нүктесі жатқан жарты жазықтықты бағдаршалармен белгілейміз. Осы жолмен қалған теңсіздіктер үшін де шешімдер жарты жазықтықтары анықталады. Нәтижесінде АВСД шешімдер көпбұрышы алынады.
- L0бастапқы түзуін жүргіземіз, яғни 3х1+3х2=0. Бұл координат осінің басынан өтетін түзудің теңдеуі. Мақсат функциясының градиентін құру үшін оның дербес туындыларын есептейміз. Бұдан мақсат функциясының ең жылдам өсу бағыты(3. 2) векторымен анықталады.
- Бастапқы түзудіградиенттің бағытында бір-біріне параллель жылжытамыз L(X) тобының тірек түзулері А және С төбелері арқылы өтеді: С нүктесінде мақсат функциясы өзінің максимумын, ал А нүктесі минимумын қабылдайды.
- Экстремальдық нүктелердің координаталарын анқтаймыз. А төбесінің координаталарын табу үшін III және IV шекаралық түзулерінің теңдеулерінен құрылған жүйені шешу керек.
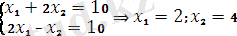
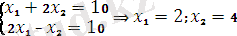 (10)
(10)
Бұдан шығатыны, А нүктесі координаттары (2, 4), ал бұл нүктедегі мақсат функциясының мәні:
L
min
=3


Осыған ұқсас С(12, 3) нүктелерінің координаталары анықталады.
L
max
=3
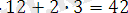
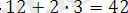 Сонымен есептің жауабы: А(2, 4) нүктесінде мақсат функциясы минимум L
min
=14, C(12, 3) нүктесінде масимум (L
max
=42) қабылдайды.
Сонымен есептің жауабы: А(2, 4) нүктесінде мақсат функциясы минимум L
min
=14, C(12, 3) нүктесінде масимум (L
max
=42) қабылдайды.
№19 нұсқа
- ɑ (х) = -5x1+ х2
Мақсат функциясының максимумы мен минимуммын келесі шектеулерде табу керек.
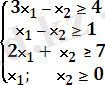
Графиктік тәсілмен
- Үш базаға 200; 270; 130 бірлікте жүк түсті. Осы жүкті 120; 80; 240; 160 бірлікті тұтынушы төрт дүкенге жеткізу керек. Ал құны тарифте матрица арқылы арқылы берілген.
Жеткізудің оптималды жоспарын және жіберілген шығынын есепеу керек.
Есептің шығару жолы:
- Графиктік тәсілмен:
ɑ(х) =-5x 1 +x 2
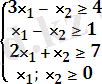
⟹
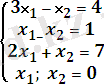
⟹
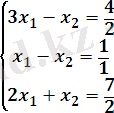
⟹
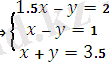
⟹
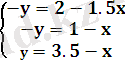
⟹
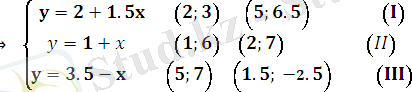
y
(I)
(II)
A
B
1 2 3 4 5 6 7 8 9 10 x
-2. 5
C (III)
ɑ(x) = -5x 1 +x 2
max (A) = -5 ∙ (-0. 5) + 4=1, 5 min (C) = -5∙2, 5 + 3, 5= -9
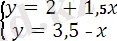
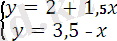
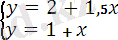
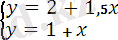
2+1, 5x=3, 5-x 2+1, 5x=1+x 2-3, 5=x-1, 5x 2-1= x+1, 5x -1, 5 = -0, 5x 1 = 2, 5x x 1 = -0, 5 x 1 = 2, 5 x 2 = 4 x 2 = 3, 5 max (A) =1, 5 min (C) = -9.
200; 270; 130. 120; 80; 240; 160.
Жіберу
орны
- Солтүстік - батыс бұрыш арқылы есепті шешу әдісі.
Жіберу
орны
2
120
4
80
8
240
12
30
3
130
S(x) =2*120+4*80+8*240+12*30+3*130=3230 ақша бірлігі.
- Минимал әдісі.
Жіберу
орны
2
100
4
30
7
40
9
30
5
20
1
50
8
200
3
13 0
C 2 = 2*100 + 4*30 + 7*40 + 9*30 + 5*20 +
+50+8*200+3*130=3010 ақша бірлігі.
IV. СЫЗЫҚТЫ ПРОГРАММАЛАУДЫҢ (СП) ТРАНСПОРТ ЕСЕБІН ПОТЕНЦИАЛДАР ӘДІСІМЕН ШЕШУ.
СП транспорт есебі келесі түрде құрылады. Мақсат функциясы
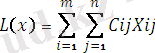
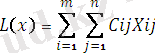
Және төменгі шарттар берілген.
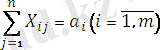
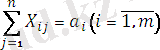 (11)
(11)
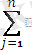
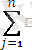 (12)
(12)
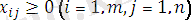
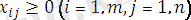 (13)
(13)
Мұндағы: С
ij
- i- ші өндірушіден j - ші тұтынушыға жүк бірлігін жеткізу құны. а
i
- і-ші өндіруші ресурстары; b
j
- j - тұтынушының қажеттілігі; (11) - (12) шарттары орындалып, кез келген і- ні өндірушіден (і=
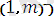
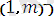 кез келген j - ші тұтынушыға (j=
кез келген j - ші тұтынушыға (j=
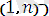
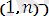 мақсат функциясы экстремум қабылданбайтындай бір текті жүкті тасымалдаудың жоспарын
мақсат функциясы экстремум қабылданбайтындай бір текті жүкті тасымалдаудың жоспарын
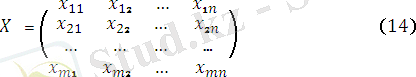
құру қажет.
1 - кесте
C 21
X 11
C 12
X 12
C 1n
X 1n
C 21
X 21
C 22
X 22
C 2n
X 2n
C m1
X m1
C m12
X m12
C mn
X mn
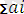
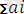

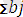
Потенциал әдісінің алгоритмі
1. Транспорт есебінің шешілу шартын тексереміз,
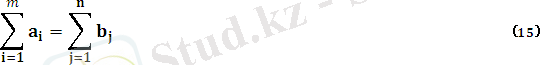
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz