Орташа шамалардың мәні, маңызы, түрлері және қолданылу шарттары


Қазақстан Республикасы Білім және Ғылым Министрлігі
Қазақ Ұлттық Аграрлық Университеті
Есеп және аудит кафедрасы
РЕФЕРАТ
Тақырыбы : Орташа шамалардың мәні, маңызы, түрлері
және қолданылу шарттары
Орындаған :
Тексерген :
Алматы 2006
Мазмұны
Кіріспе 3
1. Орташа шамалар 4
1. 1 Орташа шаманың мәні, маңызы және қолданылу шарттары 4
1. 2 Орташа шамалардың түрлері 5
2. Орташа шамаларды есептеу 7
2. 1 Арифметикалық орташа шама 7
2. 2 Үйлесімдік орташа шама 12
2. 3 Құрылымдық орташа шама 14
Қорытынды 18
Пайдаланылған әдебиеттер тізімі 19
2
Кіріспе
Ертеректе айтылғандай, статистика көптеген құбылыстар мен процестерді оқытады. Осындай әрбір құбылыс барлық жиынтыққа ортақ ерекше, жекелей қасиеттері бар. Жекелей құбылыстар арасындағы айырмашылық вариация деп аталады. Егер ыстық суы бар ыдысқа суық су құйсақ, онда ыдыстағы бар судың температурасы бірдей болады. Балабақшадағы бір топқа немесе мектептегі бір сыныпқа барған балалар да ортақ, орташа деңгейдегі мінезге ие болады. Үлкен өнеркәсіптік өндіріс стандартталусыз болмайды, яғни жиналатын механизмдер, агрегатталусыз тетіктерінің орташа өлшемі .
Сонымен, жиынтық элементтерінің өзара байланысуы вариацияның шектелуіне әкеледі. Бұл тенденция обьективті болып табылады. Сондықтан да орташа шаманың кең көлемде тәжірибе мен теорияда қолданылуы объективтілігіне байланысты.
Жұмысшының көмегінсіз болған өндірістегі жұмыс ақысы орташа бағалау немесе жалақының орташа сағаты бойынша есептелетіні әрбір жұмысшыға мәлім. Емтиханда да орташа балл осындай екеніде әрбір студентке мәлім. Орташа шама әдісі арқылы статистика көптеген есептерді шығарады .
Орташа шаманың басты көрсеткіші қорытындылау функциясында, яғни барлық құбылыс жиынтығын мінездейтін орташа шаманың көптеген әр түрлі белгілердің жеке көрсеткіштерінің ауыспалылығы. Қазіргі заман адамдарының ерекшелігі ол ұлдарының әкелерінен, сонымен қатар қыздарды да шешелерімен салыстырғанда ұзын болады. Бұл көріністі қалай өлшейміз? Әр түрлі жанұяда үлкені мен кішісінің бойларының сәйкестігі әр түрлі болып келеді. Әрқашанда ұл әкесінен, ал қыз шешесінен ұзын бола бермейді. Бірақ егер мыңдаған тұлғалардың орташа бойын өлшесе, онда орташа бой бойынша ұлдары мен әкелері, қыздары мен шешелері арасындағы бір ұрпаққа бой өсуінің орташа шамасын табуға болады .
Бұған дейін де және қазіргі нарықтық экономикаға өту кезеңінде де статистиканы оқымаған халықтың ортасынан «орта» немесе «орта есеппен» деген ұғымды көптеп естуге тура келіп жүр. Яғни, бұл сөздерді қандай жағдайда қолдана аламыз деген сұрақ-сауалдың тууы мүмкін. Мысалы, бір институтта оқитын студенттердің стипендия ларының мөлшерін алатын болсақ, онда орташа шама әдісін қолданудың ешқандай да қажеттілігі болмайды. Себебі, сол жоғарғы оқу орнындағы стипендияның мөлшері барлық студенттер үшін бірдей, тек қана өте жақсы оқитын студенттердікі ғана өзгеше болады. Ал егер жұмысшылардың орташа айлық еңбекақыларын қарастыратын болсақ, онда олардың арасында түрлі себептеріне қарай жалақы мөлшері әркімде әрқилы болады. Мұндай жағдайда барлық жұмысшыларға тән сандық көрсеткішті есептеу үшін орташа шама әдісі қолданылады.
3
Орташа шамалар.
Орташа шаманың мәні мен маңызы және қолданылу шарттары.
Статистикалық бақылаудың нәтижесінде жиналған мәліметтерді дұрыс өңдеп,
жинақтаудың әлеуметтік - экономикалық және статистикалық тәжірибеде атқаратын рөлі де өре жоғары. Бірақ, бұл көрсеткіштер зерттеп отырған қоғамдық құбылыстар мен процестерге талдау жасауға, жиынтық бірліктерін қорытындылауға жеткіліксіз. Кейбір жағдайда осы көрсеткіштер жиынтығының даму, өзгеру заңдылығын зерттеу және сол сандық мәндер жиынтығын дұрыс дәлдікпен көрсету үшін және берілген бірліктерді толық қамту үшін бәріне ортақ негізгі көрсеткіштер жүйесі керек долады. Мұндай көрсеткіштер орташа шама әдісі арқылы алынады және оны қорытындылаушы көрсеткіш деп атайды.
Орташа шама деп, біртектес жиынтықты белгілі бір жағдайда және белгілі бір уақытта өздеріне тән белгісі бойынша жинақтап көрсететін орташа сан мөлшнрін, яғни біртектес жиынтық бірліктерінің орта есеппен алынатын белгісінің барлық бірліктерге жатқызылатын сандық шамасын айтады. Мысалы, шаруашылық бойынша әр гектардан 20 центнер өнім алынған десек, онда бұл көрсеткіш бір жерде 22 центнер, ендігі бір жерде 18 центнер және тағы басқа көрсеткіш түрінде болып кездесуі мүмкін. Бірақ, 20 центнер деген сандық көрсеткіш осы шаруашылықтың орташа өнімділігінің шамасын көрсетеді.
Статистикада орташа шаманы есептегенде және қолданғанда төменде берілген принциптер мен шарттар толықтай орындалуы тиіс :
1) Зерттеп отырған құбылыстың, процестің жиынтық бірліктері біртекті болуы
шарт. Егер зерттеп отырған жиынтық бірліктері біртекті болмай, әр түрлі
болатын болса, онда осы жиынтықтарды өздеріне тән сапалық белгілері
бойынша бірнеше топтарға бөліп, әр топ үшін жеке орташа және одан кейін
жалпы орташа шама есептелінеді. Мұндай жағдайда жалпы орташа шама
құбылыстың орта мөлшерін дәл көрсетеді және нақты шындықты бейнелейді.
2) Орташа шаманы есептегенде оның жеке -дара өзгермелі сандық және
сапалық көрсеткіштері толығымен жойылады. Көп сандар заңына
байланысты негізгі белгінің әрбір бөлікке тән шамасы шығады. Атап
айтқанда, құбылыстар мен процестердің ауытқуын жекелей зерттемейді .
3) Орташа шаманың көрсеткіші статистикалық бақылау нәтижесінде
жиналған мәліметтер арқылы есептелінеді. Егер бақылау көрсеткіштері
неғұрлым көп болатын болса, соғұрлым орташа шама дұрыс шығады және
нақты шындықты көрсетеді. Себебі, осы жағдайда ғана кездейсоқ
ауытқулар өзара жойылып, бір заңдылықпен өзгерген шама ғана қалады.
Мысалы, бір цехта жұмыс істейтін үш жұмысшының айлық еңбекақысында
қарап сол цехтағы барлық жұмысшылардың орташа айлық еңбекақысын
көрсетуге болмайды, т. б.
4) Зерттеп отырған құбылыстармен процестердің жеке бөліктерінің арасында
ауытқу болатын жағдайларда орташа шама қолданылады. Сонымен,
жоғарыда келтірілген принциптер мен шарттарды еске ала отырып, орташа
4
тек статистикада ғана емес, басқа да ғылым салаларында басқару, ғылыми -
зерттеу жұмыстарында көптеп қолданылады . Себебі қоғамдық
құбылыстардың өзара байланысын, өсіңкілігін немесе кемуін сондай-ақ
статистикалық бақылау, топтау, мәліметтерге талдау жасау орташа шама әдісі
арқылы сипатталады . Яғни әлеуметтік -экономикалық құбылыстарды
зерттеу кезінде орта шаманың атқаратын рөлі өте жоғары .
Орташа шамалардың түрлері
Статистикада зерттеп отырған құбылыстар мен процестердің негізіне, алдына қойған мақсатына және бастапқы берілген көрсеткіштердің мәніне сәйкес орташа шаманың бірнеше түрі қолданылады, олар мыналар :
- арифметикалық
- геометриялық
- құрылымдық
- үйлесімдік
- шаршылық (квадраттық) орташа шамалар .
Осы көрсетілген орташа шамаларды қолдану барысында оларды қандай жолмен есептеу керек деген теориялық және тәжірибелік күрделі сұрақтар туады. Олай болса, қолда бар деректердің мәніне сәйкес орташа шаманың қандай түрін пайдалансақ, қарастырып отырған белгі варианттарының орташа мәнін дұрыс табамыз ? Мәселе осында. Оны есептеу үшін алдымен әрбір нақты жағдайда осы орташа шама нені білдіретінін, оның қандай шамалардың қатынасы арқылы есептелетінін анықтап алуымыз қажет. Содан кейін есептеп шығарылған орташа шаманың өзіне сәйкес әлеуметтік -экономикалық мағынасы болуы тиіс.
Осы принциптерді басшылыққа ала отырып орташа шаманы іс жүзінде қалай есептеуге болады ? Ол үщін «орташаның негізгі қатынасы » (ОНҚ) принципін негізге аламыз. Демек, зерттеліп отырған көрсеткіш өзіне тән сан мағынасын белгілі бір тәсілмен есептеп шығарса ғана дұрыс көрсеткіш бола алады . Оны нақты мысалдар арқылы төменде көрсетейін :
әуелі орташа шаманың негізгі қатынасы ретінде әр гектардан алынған орташа өнім қандай шамалардың қатынасынан шығатынын анықтаймыз . Оны есептеу үшін барлық егістік жерден жиналған жалпы өнімді осы жер көлемінде бөлу керек және ол төмендегідей болады :
ОНҚ =
немесе бір жұмысшының орташа айлығын есептеу үшін жалпы айлық қорын
жұмысшылардың санын бөлеміз. Онда орташа шаманың негізгі қатынасы
(ОНҚ) төмендегі түрде жазылады :
5
ОНҚ =
Егер орташа шама белгінің біртекті көрсеткішін сапалы қорытындыласа, онда ол берілген жиынтық белгісінің типтік мінездемесі болып табылады. Ол туралы 1973 жылы 20 жасқа толған орыс қыздарының типтік бойларын өлшеу туралы айтуға болады. Зейнеткерлердің бюджетіндегі азық- түлікті сатып алуға кеткен шығындарының типтік үлесін анықтауға болады.
Бірақ, берілген белгілер жиынтығы бойынша бір түрде белгілердің типтік мағыналы мінездеме ғана орташа шама ролі дұрыс сәйкестендірілмейді. Практикада қазіргі статистика көбінесе бір түрлі емес, құбылысты қорытындылайтын орташа шамаларды қолданады. Мысалы, тұрғындардың жан басына шаққанда етті тұтынудың орташа гамасы : бұл тұрғындардың арасында бір жасқа дейінгі балалар, ет қолданабайтындар, вегетарианцтар, шахтерлер, спортсмендер мен зейнеткерлер бар.
Типтік емес мұндай орташа көрсеткішке жан басына шаққандағы өндірілген Ұлттық табыс жатады. Жан басына шаққандағы ұлттық табыстың орташа шамасы әр түрлі азық - түліктерді орташа тұтыну шамасы - біріңғай халықшаруашылық жүйесі сияқты мемлекеттің мінездемесі, ол жүйелілік орташа деп аталады.
Жүйелік орталар бір кезде болатын кеңістікті немесе объектілі жүйе, сонымен қатар уақыт ұзақтылығының (жыл, он жылдық, мезгіл және т. б. ) динамикалық жүйесі ретінде мінезделеді . Мысалы уақыт кезеңін 1996 жылы Санкт -Петербургтегі ауаның орташа температурасы +5, +19 С мінездей алады. Бұл орташа шама жаздың +20, +25 С жоғарғы температурасы мен қыстық аязды, күз бен көктемді, күн мен түнді қортындылайды.
Бір жағынан бөлек жылдағы ауаның орташа температурасы Санкт -Петербургтегі климатының типтік мінезде болмайды. Себебі әр түрлі жылдағы температура ауытқуда болады. Мысалы, соңғы отыз жылда 1976 жылы +2, 90 C-тан 1989 жылы +7, 44 C- қа дейін еді. Климаттың типтік мінездемесі он жылдағы көпжылдық, орташа жылдық температура болады мысалы, 1967-1996 жылы ол +5, 05 C көрсетті. Типтік орта бірткті жиынтықтар үшін жүйелілік орталарды қорытындылайды немесе жүйелілік орталар біртекті болмаса да бірыңғай үшін типтік орталарды қорытындылайды. Бұл жағдайда типтік орталар бірде-бір рет өзгермейтін мінездемесінің берілгені бола алмайды .
Сонымен, сол зерттеуге алынған жеке-дара құбылыстардың жиынтығында өзгермелі шамалардың, яғни ауытқудың болуы орташа шаманы қолданудың және есептеп шығарудың негізгі шарты болып табылады. Міне, сонда ғана орташа шаманың көрсеткіші дұрыс шығады және соған сәйкес экономикалық талдау, қорытынды жасалынады.
6
Орташа шамаларды есептеу
Арифметикалық орташа шама
Қоғамдық құбылыстар мен процестерге әлеуметтік -экономикалық талдау, зерттеу жұмыстарын жүргізген кезде қорытындылаушы көрсеткіштерде әр түрлі орташа шамалар қолданылады. Солардың ішінде ең жиі қолданылатыны және кең тарағаны − арифметикалық орташа шама.
Арифметикалық орташа шама жалпы жиынтықтағы өзгермелі белгілердің жеке мәндерінің қосындысы болған жағдайда ғана қолданылады . Арифметикалық орташа шама біртектес бірлік көрсеткіштерінің жеке мәндерінің мағынасына қарай жай және салмақталған болып екі түрге бөлінеді.
Жиынтықта әрбір белгі тек бір рет ғана кездессе, яғни бір-ақ рет қайталанса немесе барлық белгілердің (варианттарының ) жиіліктері бірдей болса, онда орташаның жай түрі қолданылады. Ол өзгермелі белгілердің мәндерін бір-біріне қосып, одан шыққан қосындыны белгінің санына бөлгенге тең болып мына формула арқылы есептелінеді .
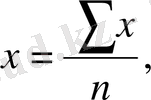
x - орташа шама ;
x - белгілердің жеке сандық мәндері ;
n - белгілердің саны ;
Σ - жиынтықтың белгісі, яғни x- тың қосындысы .
Орташа шаманың жай түрінің формуласын қолдану мен есептеу жолдарын нақты мысал арқылы көрсетейін. Мысалы, бір фирмада жұмыс істейтін 7 жұмысшының әрқайсысы 1 сағатта 70 дана, 56 дана, 69 дана, 53 дана, 61 дана, 65 дана және 67 дана тетік өңдеп шығарды десек, яғни әр жұмысшының өңдеген тетігінің шамасы бір-ақ рет кездесіп отыр. Сонда осы 7 жұмысшының орта есепппен 1 сағатта қанша тетік өңдеп шығарғанын былай есептеймін, егер орташа шаманы x деп, әр жұмысшының өңдеп шығарған тетіктердің жалпы санын Σx - деп, ал жұмысшылардың санын n - деп белгілесек, онда орташа шама мына формула арқылы есептелінеді :
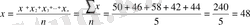 дана
дана
Демек, 7 жұмысшының әрқайсысы 1 сағатта орта есеппен 63 дана тетік шығарған .
7
Егер жиынтықтың әрбір белгісі бір рет емес, бірнеше рет қайталанатын болса, яғни жиілік бірліктерінің саны берілген болса, онда орташа шаманың салмақталған түрі қолданылады. Оны есептеу үшін әрбір қатардағы белгі мәндерін (х) жиілік көрсеткіштеріне (f) көбейтіп, одан шыққан көбейтінділердің қосындысын (Σxf) жиіліктің жалпы санына (Σf) бөлеміз және ол мына формула арқылы өрнектеледі :
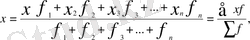
x - орташа шама ;
x - белгілердің жеке сандық мәндері ;
f - жиіліктің мәндері ;
Σxf - белгілер мен жиілік мәндерінің көбейтіндісінің қосындысы ;
Σf - жиіліктің жалпы саны .
Сонымен, орташаның негізгі қатынасы бөлімнің мәні белгілі де, алымының мәні белгісіз болған жағдайларда арифметикалық орташа шаманың салмақталған түрі қолданылады.
Арифметикалық орташа шаманың салмақталған түрін қолдану мен есептеу тәсілдерін жетік түсіну үшін төмендегі берілген мысалдарға жүгінейік :
Бірінші мысал. Төменде берілген цех жұмысшыларының дайлық еңбекақысын пайдалана отырып, бір жұмысшыға шаққандағы алынатын орташа айлық мөлшерін табу керек .
Кесте 2. 1. 1
Цех жұмысшыларының айлық еңбекақы
мөлшері бойынша бөлінуі
Жұмысшылар саны
(f)
8
Барлығы 100 жұмысшының орташа айлық еңбекақысын есептеу үшін, алдымен жалпы айлық еңбекақы қорын (Σxf) анықтаймыз .
Ол үшін әрбір топтағы айлық еңбекақыны (х) жұмысшылардың санына (f) көбейтеміз, ал содан кейін есептелген жалпы айлық еңбекақы қорын жұмысшылар санына бөлеміз. Бұл жерде арифметикалық орташа шаманың салмақталған түрінің формуласы қолданылады, яғни :
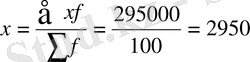 теңге .
теңге .
Сонымен, жұмысшылардың орташа айлық еңбекақысы 2950 теңге болып шықты . Демек, орташаның негізгі қатынасының мәні белгілі де, алымының мәні белгісіз болған жағдайда арифметикалық орташа шаманың салмақталған түрі қолданылады .
Егер статистикалық топтық қатарлардың белгілері бүтін шама емес, деңгей аралықты шамамен берілетін болса, онда орташа шаманы есептеу үшін алдымен әрбір топтың деңгей аралығының төменгі және жоғарғы мәндерін, екіге бөлу арқылы табамыз. Демек, деңгей аралықты қатарды бүтін шамаға айналдырамыз және оны х әрпімен белгілейміз. Содан кейін жоғарыдағы қолданылған тәсіл бойынша есептейміз .
Екінші мысал. 2. 1. 2. мәліметтерін қолдана отырып, тексеруге арналған өнімнің орташа ылғалдылығын анықтау керек .
2. 1. 2
Тексеруге арналған өнімнің орташа ылғалдылығы
Енді 2. 1. 2. - кестеде есептелінген мәліметтерге сүйене отырып өнімнің орташа ылғалдылығын анықтаймыз. Оны анықтау үшін барлық жалпы ылғалдылықты
(Σxf) тексеруге алынған өнімнің жалпы санына Σf бөлсек, бір өнімнің орташа ылғалдылығы шығады. Бұл жолы да арифметикалық орташа шаманың салмақталған түрін қолданып отырмыз, яғни
9
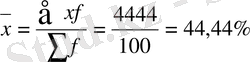
арифметикалық орташа шаманы есептеу кезінде жұмыс көлемін және есептеу жолдарын жеңілдету үшін төмендегідей математикалық қасиеттер қолданылады:
- Орташа шамамен (x) жиілік қосындысының (Σf) көбейтіндісі (хΣf) әрқашанда өзгермелі белгі мен (х) жиіліктің (f) көбейтіндісінің қосындысына (Σxf) тең болады :
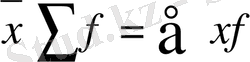
2 . Егер өзгермелі белгінің барлық жиіліктерін (f) тұрақты бір ғана (А) көбейтсек, немесе бөлсек, онда орташа шама өзгермейді :
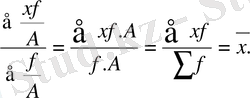
3 . Егер әр қатардағы белгілі (х) тұрақты бір (А) санды қоссақ, немесе алсақ, онда орташа шама сол тұрақты санның мөлшеріне көбейеді, не азаяды :
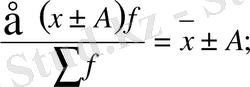 бұдан
бұдан
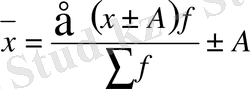
4 . Егер әр қатардағы белгіні (х) тұрақты бір санға көбейтсек, немесе бөлсек, онда жаңа белгілермен есептелген орташа шама сонша рет көбейеді, не азаяды :
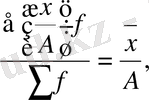 бұдан
бұдан
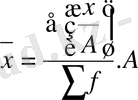
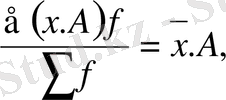 бұдан
бұдан
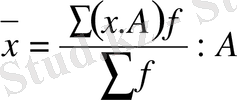
5 . Белгілердің орташа шамадан айырмаларының қосындысы әрқашанда нөлге тең болады :
Σ
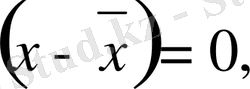 немесе Σ
немесе Σ
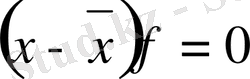
Орташа шаманы ықшамдалған жолмен есептеу. Деңгей аралықтары бірдей өзгермелі сандық қатарлар беріоген болса, онда орташа шаманы есептеу үшін жоғарыда келтірілген математикалық қасиеттерге сүйенеміз. Ол үшін барлық белгілерді (х) тұрақты бір (А) санға азайтып, одан шыққан шамаларды деңгей
10
аралығының айырма санына (d) бөлу арқылы арифметикалық орташа шаманы ықшамдалған жолмен есептеуге болады . Оны нақты мысалмен көрсету үшін
2. 1. 2- кестеге қайтадан ораламын және ықшамдалған жолмен есептелген көрсеткіштерді 2. 1. 3- кестеде көрсетемін :
Кесте 2. 1. 3
Тексеруге арналған өнімнің орташа ылғалдылығы
х - А
А = 45
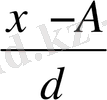
d = 2
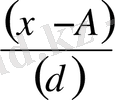 *f
*f
40-42
42-44
44-46
46-48
48-50
Барлығы :
11
25
50
9
5
100
41
43
45
47
49
-
-4
-2
0
2
4
-
-2
-1
0
1
2
-
-22
-25
0
9
10
-28
Бұл жерде алдымен А- ның шамасын табамыз. Оны табу үшін жиіліктің (f) ең үлкен мәні орналасқан, өзгермелі қатардың деңгей аралығының ортасын аламыз. Ол 45- тең (А = 45) . Содан кейін деңгей аралығының тұрақты айырма санын анықтаймыз, ол 2- ге тең (d=2) . Енді ықшамдалған жолдың бірінші мезетінің орташа шамасын анықтаймыз .
Статистикада ықшамдалған жолдың бірінші мезетін m1, әрпімен белгілейді және мына формуламен есептейді :
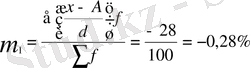
Содан соң, ықшамдалған жолмен орташа шаманы есептеу үшін бірінші мезеттің орташа шамасына (m1 = 45 ) . Онда ықшамдалған орташа шаманың фомуласы мынадай түрде жазылады және есептеу тәсілі төмендегідей :
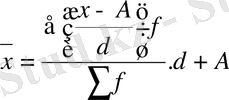 немесе
немесе
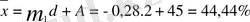
11
Сонымен, жай және ықшамдалған жолмен есептелген орташа шаманың екі мәні де бірдей көрсеткішті көрсетуде. Бірақ екінші тәсіл біріншімен салыстырғанда жедел есептелінеді және жеңілдету болады .
2. 2 Үйлесімдік орташа шама
Статистикада әлеуметтік - экономикалық көрсеткіштерге талдау және қорытынды жасау үшін арифметикалық орташа шамамен бірге Үйлесімдік орташа шама да бірге қолданылады .
Үйлесімдік орташа шама − бұл арифметикалық орташа шаманың кері және өзгертілген түрі. Егер қзгермелі қатардың белгілері (х) мен оның жиілік мәндері
(f) берілген болса, онда арифметикалық орташа шама қолданылады. Ал, кейбір жағдайда, керісінше, өзгермелі қатардың белгілері (х) мен оның жиіліктерінің көбейтіндісі (хf) беріліп, жиілік мәндері (f) белгісіз болуы мүмкін. Онда орташа көбейткішті есептеу үшін үйлесімдік орташа шаманы қолдануға болады .
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz