Сызықтық регрессия моделі: ең кіші квадраттар әдісі, бағалау шарттары және статистикалық тексерулер


СЫЗЫҚТЫҚ РЕГРЕССИЯ МОДЕЛІ
Экономикалық айнымалылардың сызықтық байланысын бағалау
Экономикалық көрсеткіштердің арасындағы өзара байланыстарды анықтау - эконометриядағы негізгі проблемалардың бірі. Кез келген экономикалық политиканың негізі - ол экономикалық айнымалыларды реттеу, демек, бұл айнымалылардың басқа айнымалыларға қалай әсер етуін білудің маңызы өте зор.
Мысалы, нарықтық экономикада инфляция қарқынын тікелей өзгертуге болмайды, бірақ оған салық-бюджеттік және қаржы-кредиттік саясат арқылы әсер етуге болады. Сондықтан дербес жағдайда ақшаны ұсыну көлемі мен баға деңгейінің арасындағы байланыс зерттелуге тиіс. Экономикалық модельдерді кұру, тексеру және жақсарту нақты статистикалық деректерді пайдаланып, статистикалық талдау жасаусыз мүмкін емес.
Экономикалық көрсеткіштер арасындағы байланыстарды зерттеуді екі айнымалы (х пен у) жағдайын қарастырудан бастаймыз.
Бұл - ең қарапайым жағдай және графиктік түрде қарастыруға мүмкіндік береді.
X пен У айнымалыларының арасындағы 2 түрлі байланысты қарастыруға болады:
1) Қандай айнымалы тәуелді, қандай айнымалы тәуелсіз екені белгісіз. Бұл жағдайда айнымалылар тең құқылы және олардың арасындағы байланысты коореляциялық талдау арқылы зерттейді.
2) Айнымалылар тең құқылы емес, яғни олардың бірі - тәуелсіз (анықтағыш), екіншісі - тәуелді (анықталатын) айнымалы болады. Демек, біріншісінің өзгеруі екіншісінің өзгеруінің себебі болады. Мысалы, табыстың өсуі түтынудың өсуіне алып келеді, валюта курсының өсуі таза экспорттың кемуіне алып келеді, проценттік норманың кемуі инвестицияның өсуіне, валюта курсының өсуі таза экспорттың кемуіне алып келеді.
Бұл жағдайда Ү = f(X) регрессия теңдеуі бағалануы керек.
Анықтама. Экономикалық айнымалылар арасындағы статистикалық байланыстың формуласын регрессия теңдеуі дейді. Егер бұл формула сызықтық болса, онда сызықтық регрессия дейді.
Анықтама. Екі айнымалы арасындағы статистикалық байланыс формуласы жұптық регрессия, көп айнымалылар арасындағы формула көптік регрессия болады.
Мысал. Кейнс жеке тұтыну С пен табыс У арасындағы сызықтық байланысты ұсынды: С = С 0 +bУ, мүндағы С 0 - автономдық тұтыну көлемі,
b (0 < b < 1) - шектік тұтыну көлемі коэффициенті.
Анықтама. Айнымалылар арасындағы байланыс формуласын - таңдаулы регрессия теңдеуін спецификациялау деп атайды.
Бірақ С 0 және b параметрларынын сандық мәндері бағаланғанша және олардың шындылығы тексерілгенше, бұл формула тек гипотеза болып қалады. Параметрлер мәндерін қалай тауып, шындылығын қалай тексереді? Төмендегі графиктерді қарастырайық.
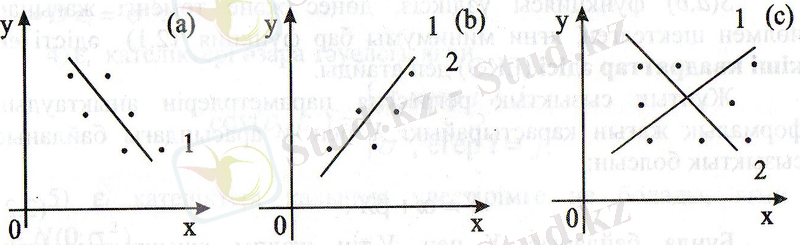
- (а) графигінде X пен У арасындағы байланыс сызықтыққа жақын. (1) - түзу бақылау нүктелеріне жақын, олардың ауытқуы -кездейсоқ әсерлердің нәтижесі;
- (b) графигінде X пен У арасындағы байланыс сызықтық емес (2) функциямен анықталады. Кез келген түзу, мысалы (1), бақылау нүктелерінен көп ауытқиды.
- (с) графигінде X пен У арасында байланыс жоқ; қандай да бір байланыс формуласын алсақ та, параметрлеу нәтижесі сәтсіз болады. Мысалы, (1) және (2) түзулері "бұлттың" ортасы арқылы өтеді, қарама-қарсы жантаю коэффициенттері бар, екеуі де дұрыс емес.
Жұптық сызықтық регрессия. Ең кіші квадраттар әдісі
Эконометриялық талдаудың алғашқы пунктінде барлық сызықтық регрессия қарастырылады. Егер қандай да бір бақылау нүктелерінің "бұлты" берілсе, онда осы нүктелер жиынына "ең жақын" болатын түзуді анықтау керек. Әдетте, жақындылық критерийі ретінде тәуелді айнымалының нақты мәндері у і -мен регрессия теңдеуі бойынша есептелген теоретикалық мәндердің айырмасының қосындыларының квадратының минимумы алынады:
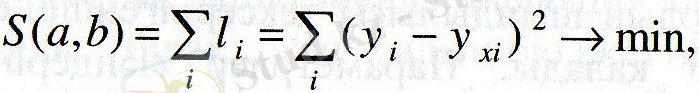
мұндағы у хі = а + bх, регрессия теңдеуі бойынша есептелген мәндер; х і , у і - бақылау деректері; а, b - белгісіз параметрлер.
S(а, b) функциясы үздіксіз, дөңес және төменгі жағынан нөлмен шектелген, яғни минимумы бар функция. Осы әдісті ең кіші квадраттар әдісі (ЕКӘ) деп атайды.
Жұптық сызықтық регрессия параметрлерін анықтаудың формалық жағын қарастырайық. X пен У арасындағы байланыс сызықтық болсын:
Ү=α+βХ.
Бұнда байланыс X пен У-тің жалпы жиынтықтарының арасындағы байланыс болады. Бірақ У-ке басқа да ескерілмеген факторлар әсер етеді және өлшеу қателіктері де болуы мүмкін.
Демек, x і және у і тәжірибелік деректер арасындағы байланыс төмендегідей болады:
у і = α + βх і + і .
мұндағы і - кездейсоқ қателіктер (ауытқулар) .
Енді біздің алдымызда мынадай есеп тұр: тәжірибелік деректер х і , у і бойынша S шамасына min әперетіндей α және β параметрлерін бағалау керек.
Егер і ауытқуларының дәл мәндері белгілі болса, онда сызықтық формула тура болған жағдайда α және β параметрлерінің мәнін есептеуге болатын еді. Бірақ кездейсоқ ауытқулардың іріктемедегі мәндері белгісіз, сондықтан х і , у і бақылау мәндері бойынша тек α және β бағалауын таба аламыз. Бұл бағалаулар кездейсоқ болады, себебі кездейсоқ іріктемеге сәйкес келеді.
а және b сәйкес және β параметрлерінің бағалауы болсын. Онда бағаланған регрессия теңдеуі
Уі =α+βx і +ℓ і
мұндағы ℓ і - сәйкес і қателіктерінің тәжірибелік мәндері.
Ең кіші квадраттар әдісі бойынша табылған а және b бағалаулары керекті қасиеттерге ие болуы үшін, мынадай шарттар орындалады дейік:
1) і шамалары - кездейсоқ айнымалылар;
2) і қателіктерінің математикалық күтімі нөлге тең, яғни М і = 0;
3) і қателіктерінің дисперсиясы тұрақты шама, яғни D і = D і = 2 ;
4) і қателіктері өзара тәуелсіз, яғни
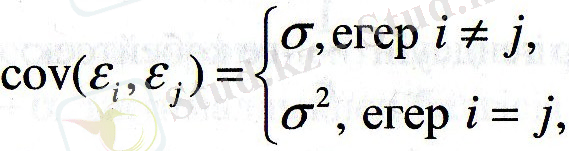
5) і қателіктері қалыпты үлестірімге ие болады, яғни і ϵ N(0; 2 ) .
Егер алдындағы шарттары орындалса, онда ең кіші квадраттар әдісі бойынша табылған бағалар мынадай қасиеттерге ие болатыны теориядан белгілі:
а) Бағалар ауытқымаған, яғни
Ма =α, Мb =β.
Бұл қасиет М і = 0 шартынан шығады, яғни бағалау барысында жүйелік қателіктер болмайды.
б) Бағалар тиянақты, яғни бақылау саны өскен сайын бағалар дисперсиясы 0-ге ұмтылады:
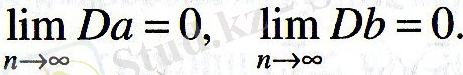
Басқаша айтқанда, n өскен сайын бағалар шындылығы өседі.
в) Бағалар тиімді, яғни бұл параметрлердің кез келген у бойынша сызықты бағаларының ішінде ең кіші дисперсияға ие болады.
Жазылатын шарт бағаларының статистикалық шындылығын тексеру үшін қолданылады. Бұл шарт орындалғанда, бағалар барлық ауытқымаған бағалар ішінде ең кіші дисперсияға ие болады.
Енді а және b бағаларын табайық.
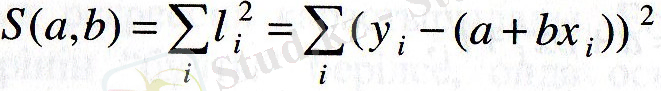 функциясы минимумге жетуі үшін, дербес туындыларын 0-ге теңестіру керек.
функциясы минимумге жетуі үшін, дербес туындыларын 0-ге теңестіру керек.
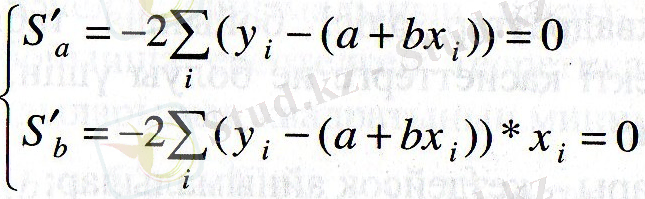
Бұдан
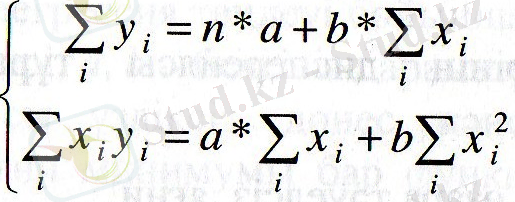
Осы жүйенің әрбір теңдеуін
 -ге көбейтсек:
-ге көбейтсек:
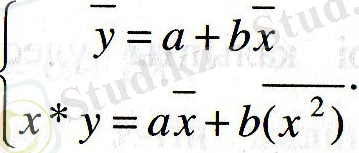
Бұдан
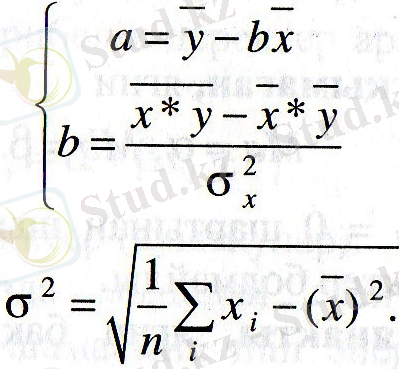
b коэффициенті табудың мынадай формулалары да бар:
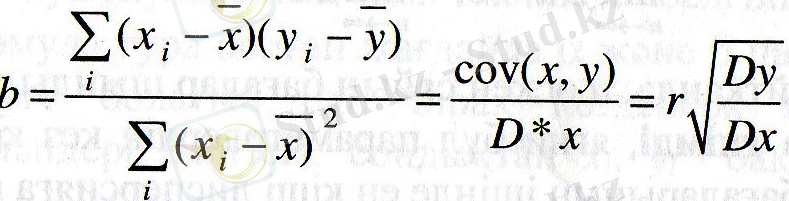
Регрессия коэффициенті b-ны тексеру үшін төмендегі теңсіздік орындалуы керек:
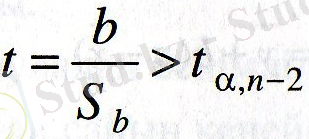
Мұндағы
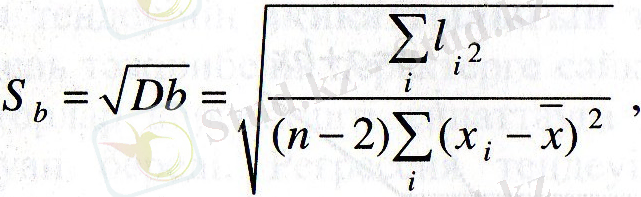 b-ның стандарт ауытқуы, t
α, n-2
- Стьюденттің t үлестірімі.
b-ның стандарт ауытқуы, t
α, n-2
- Стьюденттің t үлестірімі.
Ескере кететін жай, егер корреляция коэффициенті r шын болса, онда регрессия коэффициенті b-да шын болады.
Аралық бағалау және регрессия теңдеуінің ақиқаттығын тексеру
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz