Логикалық программалауда унификация алгоритмі мен жалпыланған Модус Поненс арқылы алгоритмнің негіздемесі


Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 26 бет
Таңдаулыға:
Реферат
Бітіру жұмысы 23 беттен, теориялық және практикалық жұмыстар көрcетілген кіріспеден, негізгі екі бөлімнен, қорытындыдан, қолданылған әдебиеттер тізімінен тұрады.
Бітіру жұмысының негізгі мақсаты: логикалық программалаудың ең негізгі ерекшеліктерінің бірі - программалау есебін шешуде, есептің алгоритмі жазылмайды, Осы жазылмаған алгоритмді мақсат ете отырып, оның негіздеуін, предикаттар логикасының тіліне сүйеніп үлкен екі жақтан, яғни унификациялау және қорыту(жалпыланған Модус Поненс ережесі) арқылы дәлелдеулері қарастырылады. Оларға қатысты мысалдар беріліп, осы ұғымдардан туған жаңа теоремалар дәлелденіп, көрсетілген.
Пайдаланылған сөздер (терминдер) : терм, атомарлық формула, өрнек, унификатор, іздеу ағашы, мақсаттар тізбегі (goal) .
Мазмұны
Алғысөз 4 бет
Логикалық программалаудың тілі 5 бет
Логикалық өрнектер тілі ерекшеліктері 6 бет
Унификациялау 8 бет
Унификация алгоритмі 10 бет
Ең жалпы унификаторды табу алгоритмі 12 бет
Логикалық программалаудағы негізгі қорыту ережесі 17 бет
Мақсатттарды жүзеге асыру 18 бет
Қорытынды 21 бет
Қолданылған әдебиеттер тізімі 22 бет
Алғы сөз
Логикалық программалау “пролог” табиғи тілдегі сөйлемдердің граматикалық мәселелерін талқылау үшін және мәтін есептерді шешу үшін Шотландияда дүниеге келген.
Математикалық логика саласында зерттеу жасап жүрген Франция мен Англиядағы екі үлкен топтағылардың бірі, тілдерді анықтайтын программаны, ал екінщісі - математикалық сөйлемдерді анықтайтын программаны ойлап табуды көздеулерінің нәтижесінде, екеуі біріге келе осы тілдің құрылуына себепкер болған.
Ұсынылып отырған жұмыста - логикалық программалаудың алгоритмінің негіздеуін алу үшін, осы тілге байланысты алғашқы негізгі мәліметтерден бастап, рет- ретімен жүйелі түрде мақсатқа жол салынған. Педикаттар логикасының көмегімен унификациялау және ең жалпы ортақ унификаторды табу алгоритмін табуды дәлелдеп шығарып алдық. Осы негізде оның қорытындысын таптық. Яғни, егер берілген өрнектер белгілі бір 𝜃 деген ауыстыру арқылы теңелсе, онда оның ең жалпы ортақ унификаторы және ең жалпы ортақ мысалы бар екнін дәлелдедік, егер жоқ болса, онда оларды унификацияланбайтынын дәлелдедік.
Екінші негізгі бөлімде - жалпыланған Модус Поненс арқылы алгоритмнің негіздеуін көрсеттік. Бізде мақсаттар тізімі болса, онда оны жүзеге асырудың екі жолын қарастырдық. Яғни, қарапайым формулалар тізбегінен және іздеу ағашынан тұратын алгоритмдер көрсетілді.
Логикалық программалаудың тілі
Басқада программалау тілдеріне ұқсас логикалық программалауда өз алдына белгіленген төмендегідей тілдік жүйелерден тұрады.
Альфавит:
- сигнатура
- логикалық байланыстар(кванторлар)
- айнымалылар
- техникалық белгілер
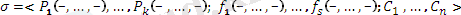
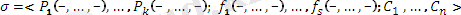
Мұндағы

 предикаттар,
предикаттар,

 функцияналдар,
функцияналдар,

 тұрақтылар. Предикаттық, функционалдық және тұрақтылар символдарының жиынын сигнатура деп,
σ
арқылы белгілеймыз.
тұрақтылар. Предикаттық, функционалдық және тұрақтылар символдарының жиынын сигнатура деп,
σ
арқылы белгілеймыз.
құрамындағы айнымалының әрбір мәніне сәйкес жаңа пікір білдіретін
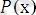
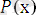 өрнегін бір орынды предикат деп, Ал
өрнегін бір орынды предикат деп, Ал

 орынды предикат деп, құрамындағы
х
1
,
х
2
, …,
х
n
айнымалыларына нақты мәндер бергенде, пікірге айналатын P(
х
1
,
х
2
, …,
х
n
) өрнегін түсінеміз.
орынды предикат деп, құрамындағы
х
1
,
х
2
, …,
х
n
айнымалыларына нақты мәндер бергенде, пікірге айналатын P(
х
1
,
х
2
, …,
х
n
) өрнегін түсінеміз.
Логикалық программалаудағы өрнектер
Өрнек - терм немесе атомарлық формула.
Терм:
не тұрақты не айнымалы не

 орынды функционалдық символ болса, онда келесі түрдегі
орынды функционалдық символ болса, онда келесі түрдегі
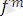
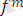 (
(

 ) функционалдық әрпі бар мән болады. мұндағы
) функционалдық әрпі бар мән болады. мұндағы

 термдер. Әрбір терм осы ережелерді ақырлы рет қолдану арқылы кұрылады.
термдер. Әрбір терм осы ережелерді ақырлы рет қолдану арқылы кұрылады.
Мысалы, v айнымалы символы мен f 1 - 1 орынды функционалдық символынан ғана тұратын барлық термдер тізімі мынандай:
v , f 1 ( v ), f 1 ( f 1 ( v ) ), …, f 1 (… f 1 ( v ) …), …
Термдердің қасиеттерін термнің күрделілігі бойынша индукцияны пайдаланып дәлелдеу.
Жоғарыдағы анықтама термдердің күрделілігі бойынша индукцияға құрылған. Сондықтан, термдердің қандай да бір
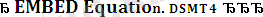
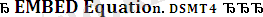 қасиетін индукция арқылы дәлелдеу келесі тәртіппен жүреді.
қасиетін индукция арқылы дәлелдеу келесі тәртіппен жүреді.
- Тұрақтылар үшінқасиетінің орындалатынын тексереміз.
- Айнымалылар үшінқасиетінің орындалатынын тексереміз.
- Алдыңғы тексерістер оң нәтиже берсін. Онда егерfm- кез келгенmорынды функционалдық символ, Егерқасиеті осы үш шарттың барлығын қанағаттандырса, ондақасиеті берілген тілдің барлық термдері үшін орындалады.
Ал t 1 , …, t m -
Күрделілігі 0 болатын терімдер:

 , …яғни кезкелген тұрақтылар,
, …яғни кезкелген тұрақтылар,
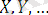
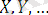 яғни кезкелген айнымалылар.
яғни кезкелген айнымалылар.
Күрделілігі
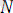
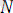 болатын терім:
болатын терім:
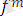
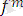 (
(

 ) . Мұндағы
) . Мұндағы

 -күрделілігі 0 болатын терм.
-күрделілігі 0 болатын терм.
Атомарлық формула(қарапайым) :
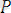
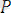 предикат,
предикат,

 терм,
терм,

 орынды предикаттық символ болса, онда
орынды предикаттық символ болса, онда
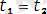
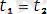 болған кездегіні немесе
болған кездегіні немесе
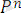
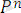 (
(

 түріндегі сөзді атомарлық формула дейміз. Мұндағы
түріндегі сөзді атомарлық формула дейміз. Мұндағы

 терімдер.
терімдер.
Мысалы. Eгер Р 2 екі орынды предикаттық символ, ал f 1 бір орынды функционалдық символ болса, онда
Р
2
(
v
,
v
),
Р
2
(
v
,
f
1
(
v
) ),
Р
2
(
f
1
(
v
),
f
1
(
f
1
(
v
) ) ),
v
=
v
,
f
1
(
v
) =
v
сөздерінің әрқайсысы атомaрлық формуланың мысалдары болады.
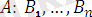
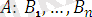 ,
,
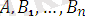
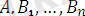 - атомарлық формула болады.
- атомарлық формула болады.
Формулалар:
- Қарапайым формулалар:(; термдер.
- мұндағы, В қарапайым формулалар, бұл программалау тілінде блай , .
Логикалық программалау тілі ерекшеліктері
Формуланың түрлері:
(*)
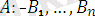
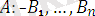
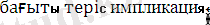

 коньюнкция(&)
коньюнкция(&)

 дизьюнкция(
дизьюнкция(
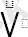
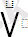 )
)

 терістеу(not)
терістеу(not)
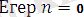
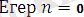 болса, онда шарты жоқ деген сөз. Формула n=0 деп жазылады.
болса, онда шарты жоқ деген сөз. Формула n=0 деп жазылады.

 ксиомалар түрі әрқашан (*) формулаға ұқсас.
ксиомалар түрі әрқашан (*) формулаға ұқсас.
Теория:
кез келген пікірлер логикасының формулаларын логикалық программалау тілінің формулаларына ауыстыру арқылы пайда болған формуланы логикалық программалау тілі программасының
аксиомалары
деп атаймыз.
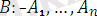
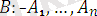 , …,
, …,
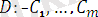
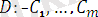 осындай бірнеше формулалар тізбегі
теория
деп аталады. теория логикалық программалау тілінің программасында,
осындай бірнеше формулалар тізбегі
теория
деп аталады. теория логикалық программалау тілінің программасында,

 аксиомалар тізбегінен тұрады. Логикалық программалауда теорияны анықтау үшін, алдымен тілді анықтау керек. Программалау тілімен, берілген теорияны пайдалана отырып есеп шығару барысында, программа құрамына есептің логикалық программалау тіліндегі берілісін жазамыз. Мақсаттар тізімінде (goal) сұрақтар қоямыз. Программа алгоритмі жазылмайды. Алгоритм логикалық программалаудың негізгі деталы ретінде программаның өз ішіне енгізілген. Біз осы алгоритмді барлық зерттеулердің басты мақсаты етіп, ешқандай программалау кітаптарында дәлелденбеген программаның негіздеуін, математикалық жолмен үлкен екі тақрыпқа бөліп дәлелдеу жүргіземіз. Олар: унификациялау ережесі және жалпыланған Модус поненс ережесі. Негіздеуді осы ережелерге мысалдар келтре отрып дәлелдейміз.
аксиомалар тізбегінен тұрады. Логикалық программалауда теорияны анықтау үшін, алдымен тілді анықтау керек. Программалау тілімен, берілген теорияны пайдалана отырып есеп шығару барысында, программа құрамына есептің логикалық программалау тіліндегі берілісін жазамыз. Мақсаттар тізімінде (goal) сұрақтар қоямыз. Программа алгоритмі жазылмайды. Алгоритм логикалық программалаудың негізгі деталы ретінде программаның өз ішіне енгізілген. Біз осы алгоритмді барлық зерттеулердің басты мақсаты етіп, ешқандай программалау кітаптарында дәлелденбеген программаның негіздеуін, математикалық жолмен үлкен екі тақрыпқа бөліп дәлелдеу жүргіземіз. Олар: унификациялау ережесі және жалпыланған Модус поненс ережесі. Негіздеуді осы ережелерге мысалдар келтре отрып дәлелдейміз.
Мысал ретінде
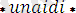
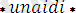 деген атпен жазылған мына программаны қарастрайық:
деген атпен жазылған мына программаны қарастрайық:
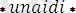
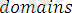
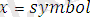
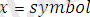
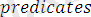
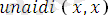
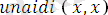
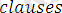
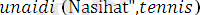
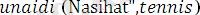 .
.
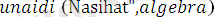
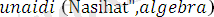 .
.
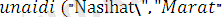
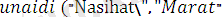 ) .
) .
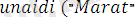
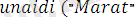 ,
,
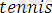
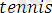 ) .
) .
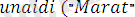
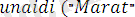 ,
,
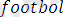
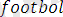 ) .
) .
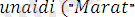
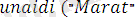 , ) .
, ) .
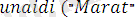
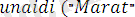 , ) .
, ) .
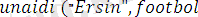
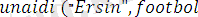 ) .
) .
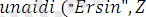
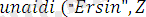 ) :
) :

 unaidi (), Z<>
unaidi (), Z<>
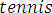
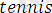 .
.
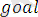
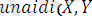
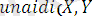 ) .
) .
Бұл программа
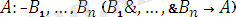
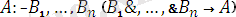 формулалар негізінде түзілген.
формулалар негізінде түзілген.
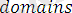
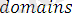 қарастрылған программаның облысын анықтайды.
қарастрылған программаның облысын анықтайды.
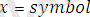
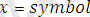 тұрақтылардың облысы. мұнда тұрақтылар кішкене әріппен және трнақша ішіне жазылады.
тұрақтылардың облысы. мұнда тұрақтылар кішкене әріппен және трнақша ішіне жазылады.
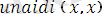
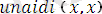 предикат, аргументтері.
предикат, аргументтері.
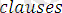
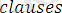 аксиомалар тізбегі немесе жалпы түрде теорияны құрайды.
аксиомалар тізбегі немесе жалпы түрде теорияны құрайды.
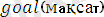
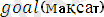 теорияны қорту үшін, негізгі мақсатқа орай сұрақтар қояды.
теорияны қорту үшін, негізгі мақсатқа орай сұрақтар қояды.
Логикалық программалау тілінде айнымалыны терммен ауыстыру
- Белгілі қандай да бірtтермімен ауыстыру үшін бос болуы керек. Егер бос болмаса, алдымен формуладағы байланған айнымалының атын өзгертіп алып, аталған айнымалыны терммен ауыстырамыз. орнына қою үшін ∃уS(v, у, z) формуласындаудіuмен ауыстырсақ, бастапқы формулаға парапар ∃uS(v, u, z) формуласын аламыз. Ал бұл үшін бос. Яғни, ∃uS(t, u, z) бастапқы ∃uS(v, u, z) формуласынан ауыстыру арқылы алынған болып шығады.
- термді тек бос айнымалының орнына қою мен қатар, формулада кездесетін айнымалыларының, квантордың әсер аймағында не болмаса формула құрамына терімді енгізгеннен кейін өзінің қайталанып түспеуін тексеру керек. орнынатермін қойсақ, формуласын аламыз. Алформуласымен мағынасы орнынатермін қойсақ, мағынасы өзгергенформуласын аламыз.
Унификациялау операторы

 тілдегі өрнек.
тілдегі өрнек.
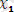
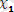 , …,
, …,
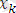
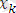
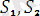
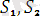 ге кіретін айнымалылар
ге кіретін айнымалылар
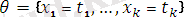
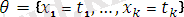 ауыстыруы болсын.
ауыстыруы болсын.
Егер
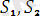
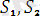 өрнектер үшін қандайда бір
өрнектер үшін қандайда бір
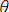
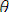 ауыстыруын қолданғанда
ауыстыруын қолданғанда
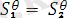
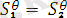 теңдігін қанағаттандыратын болса, онда
теңдігін қанағаттандыратын болса, онда
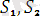
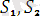 унификацияланатын өрнектер дейміз. Мұндағы
унификацияланатын өрнектер дейміз. Мұндағы
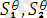
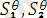 дегеніміз
дегеніміз
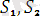
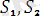 өрнектеріндегі
өрнектеріндегі
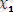
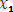 айнымалысының орнына
айнымалысының орнына
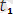
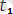 термін сол сияқты
термін сол сияқты
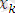
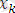 айнымалысының орнына
айнымалысының орнына
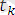
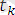 термін қойғанда шыққан өрнектер
термін қойғанда шыққан өрнектер
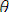
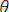 ауыстыруын (түрлендіруін)
ауыстыруын (түрлендіруін)
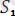
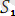 мен
мен
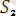
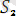 ның унификаторы деп атаймыз. Яғни
унификатор дегеніміз
-{
ның унификаторы деп атаймыз. Яғни
унификатор дегеніміз
-{
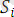
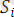 }өрнектер жиынындағы өрнектерді бірдей қылатын түрлендіру.
}өрнектер жиынындағы өрнектерді бірдей қылатын түрлендіру.
Анықтама
Өрнектер жиыны {
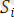
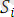 }
}
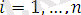
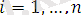 унификацияланаған
деп аталады, егер
унификацияланаған
деп аталады, егер
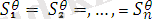
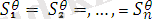 теңдіктерін қанағаттандыратын
теңдіктерін қанағаттандыратын
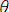
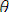 унификаторы табылса.
унификаторы табылса.
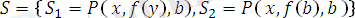
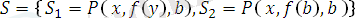 өрнектер жиыны берілсін. Онда
өрнектер жиыны берілсін. Онда
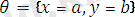
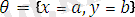 унификаторын қолданғаннан кейін, нәтижеде екі өрнек ортақ бір түрге Унификацияланған болады. Яғни
унификаторын қолданғаннан кейін, нәтижеде екі өрнек ортақ бір түрге Унификацияланған болады. Яғни
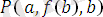
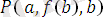 түрінде. Бұл түрлендіруді алу үшін
түрінде. Бұл түрлендіруді алу үшін
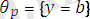
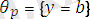 түрлендіруін қолдану жеткілікті. Біз сонда
ортақ мысал
табамыз, осыдан
түрлендіруін қолдану жеткілікті. Біз сонда
ортақ мысал
табамыз, осыдан
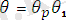
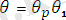 , мұнда
, мұнда
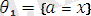
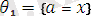 болады.
болады.
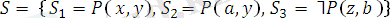
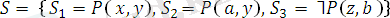 бұл өрнектер жиыны унификацияланбайды, себебі ешқандай ауыстру оның ортақ формуласын немесе терістеуіне әкелмейді.
бұл өрнектер жиыны унификацияланбайды, себебі ешқандай ауыстру оның ортақ формуласын немесе терістеуіне әкелмейді.
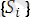
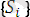 өрнектер жиыны үшін,
ең жалпы унификатор
болып
өрнектер жиыны үшін,
ең жалпы унификатор
болып
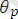
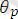 ауыструы жарайды, егер кез-келген
ауыструы жарайды, егер кез-келген
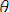
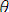 унификаторы үшін
унификаторы үшін
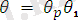
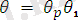 орындалса.
орындалса.
Анықтама
Өрнектер жиынының сәйкессіздік жиыны
деп-төмендегі өрнектер жиынында көрсетілген сол жақ бірінші жағдайдағы сәйкессіз ерекшеленген терімдер жиынтығын атаймыз.
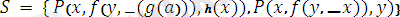
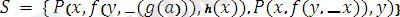 өрнектер жиыны үшін сәйкессіздік жиыны
өрнектер жиыны үшін сәйкессіздік жиыны
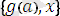
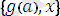 жиыны болып табылады. Себебі сол жақтағы бірінші өрнектегі
жиыны болып табылады. Себебі сол жақтағы бірінші өрнектегі
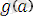
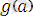 терімі сәйкесінше екінші өректің сол жақ орнындағы
терімі сәйкесінше екінші өректің сол жақ орнындағы

 айнымалысына сәйкес емес.
айнымалысына сәйкес емес.
Мысалы:
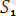
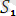
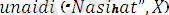
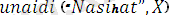
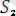
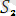
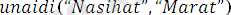
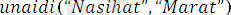


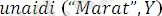
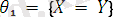

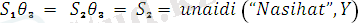
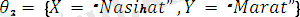
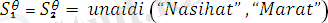
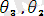
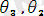 ден жалпыланған түрі.
ден жалпыланған түрі.
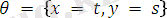
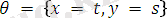 бұл унификатордың жалпы түрі.
бұл унификатордың жалпы түрі.
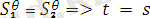
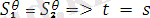
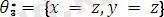
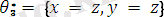 осындай негізде кез-келген ортақ мысалды жасай аламыз.
осындай негізде кез-келген ортақ мысалды жасай аламыз.
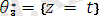
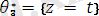
(
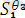
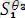 )
Ө*
=
)
Ө*
=
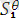
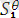 , (
, (
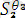
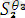 )
Ө*
=
)
Ө*
=
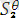
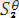
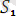
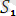 мен
мен
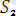
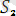 өрнектер үшін
өрнектер үшін
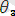
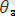 ең жалпы унификатор. Себебі кез-келген унификатыр алсақ, онда
ең жалпы унификатор. Себебі кез-келген унификатыр алсақ, онда
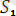
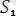 мен
мен
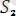
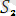 ның ортақ мысалы
ның ортақ мысалы
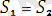
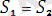 (
(
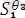
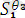 )
Ө*
осы бойынша
)
Ө*
осы бойынша
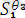
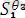 =
=
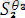
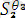 ең жалпы ортақ мысал болады.
ең жалпы ортақ мысал болады.
Унификация алгоритмі
Анықтама
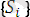
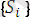 унификацияланған өрнектер жиынының ең жалпы унификаторын табатын немесе өрнектер жиыны унификацияланбаса, оның жоқтығы жөнінде хабар беретін алгоритымды
унификация алгоритымы
деп атаймыз.
унификацияланған өрнектер жиынының ең жалпы унификаторын табатын немесе өрнектер жиыны унификацияланбаса, оның жоқтығы жөнінде хабар беретін алгоритымды
унификация алгоритымы
деп атаймыз.
Бізге екі өрнек берілсін, осы екеуі үшін унификация алгоритмін қарастрайық. Әр өрнекке алгоритмнің әрбір бөлігінде түрлендіру қолданылады. Белгілі бір
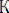
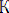 алгоритмінде:
алгоритмінде:
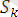
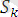 өрнектер жиыны,
өрнектер жиыны,
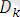
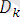 сәйкессіздіктер жиыны,
сәйкессіздіктер жиыны,
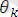
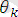 орындалатын ауыстру.
орындалатын ауыстру.
Унификация алгоритмі төмендегілерден тұрады:
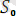
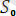 бастапқы өрнектер жиыны,
бастапқы өрнектер жиыны,
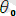
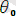
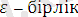
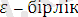 (ештеңе өзгертпейтін түрлендіру)
(ештеңе өзгертпейтін түрлендіру)
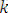
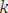 алгоритмінде:
алгоритмінде:
- егер, онда алгоритм соңықортынды түрлендіруіең жалпы унификатор.
- егерқұрамында айнымалы жоқ болса, онда алгоритм соңында өрнектер жиыны унификацияланбайды.
- егер сәйкессіздіктер жиынында айнымалыжәне термбар болса жәнек, құрамында болса, онда алгоритм соңында өрнектер жиыны унифликацияланбайды.
Болмаған жағдайда
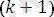
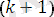 қадамына көшеміз.
қадамына көшеміз.
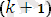
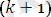 алгоритмінде:
алгоритмінде:
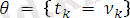
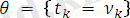 ,
,
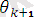
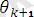 =
=
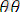
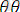 к
,
к
,
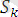
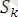 құрамына кіретін әрбір өрнек үшін түрлендіру жасаймыз.
құрамына кіретін әрбір өрнек үшін түрлендіру жасаймыз.
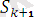
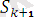 =
=
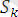
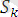 θ (немесе
θ (немесе
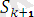
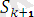 = S
0
= S
0
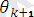
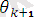 )
)
Ескерту
Егер өрнектер саны екіден көп болса, онда бірінші өрнек тізбекшесін екіншісінен унификациялайды. Одан кейін нәтижесі үшіншісімен т. с. с барлық өрнектер жиыны унификацияланғанға дейін немесе унификациялау мүмкін болмағанға дейін жалғасады.
Тұжырымдама

 cоңғы өрнектер жиыны болсын. Унификация алгоритмі өз жұмысын аяқтағанда, өрнектер жиыны унификацияланатын болса, онда ортақ унификаторын S табады немесе
cоңғы өрнектер жиыны болсын. Унификация алгоритмі өз жұмысын аяқтағанда, өрнектер жиыны унификацияланатын болса, онда ортақ унификаторын S табады немесе

 жиыны унификацияланбаған дығы жөнінде ақпарат береді. (яғни унификаторы жоқтығы жөнінде) .
жиыны унификацияланбаған дығы жөнінде ақпарат береді. (яғни унификаторы жоқтығы жөнінде) .
Осы келтірілген алгоритмнің қолданылуына төмендегі өрнектер түріндегі екі есепті қарастырайық. Бұл есептердің қортылу алгоритмі біздің программа түріндегі есептердің шығарылу алгоритмін береді.
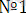
 есеп:
есеп:
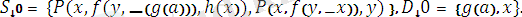
- яғниайнымалысытермнің құрамына кірмейді.
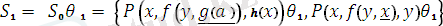
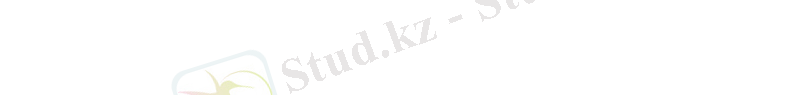
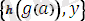
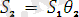
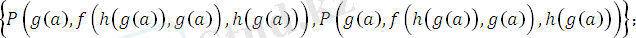
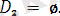
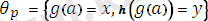
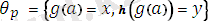 ең жалпы унификаторы алгоритм соңында.
ең жалпы унификаторы алгоритм соңында.
№2

 есеп:
есеп:
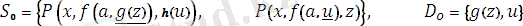
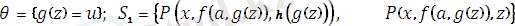
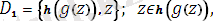
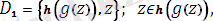 алгоритм соңында жиын унификацияланбайды.
алгоритм соңында жиын унификацияланбайды.
Унификация резолюция әдісінің негізгі бөлігі бойныша табылады. Ал унификация алгоритмі - Пролог логикалық программалау тілінің негізгі механизмі.
A мен B ны күрделілігі бойынша индукция арқылы немесе терімнің қасиетінің индукция алгоритымін пайдалану арқылы дәлелдеу жүргіземіз.

- болған кезде(болмаса, end яғыный ең үлкен ортақ унификатр жоқ) .
- болған кезде(болмаса, end) .
- т1мен s1үшін ең жалпы унификатрды іздейміз, егер орындалса онда t2мен s2үшін осылай рет -ретімен жалғастырамыз.
- жәнетермдері үшінболған кезде.
Мысал:
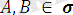
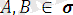 тілдегі өрнек болсын. Ең үлкен унификатрды және ең жалпы ортақ мысалды тап.
тілдегі өрнек болсын. Ең үлкен унификатрды және ең жалпы ортақ мысалды тап.
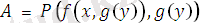
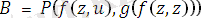
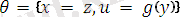
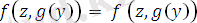
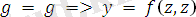
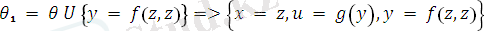
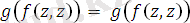
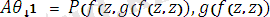
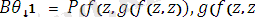
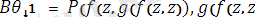 ) )
) )
Есептің шешімі бойынша, ең үлкен унификатр
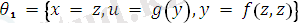
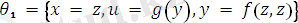 , ең жалпы ортақ мысал
, ең жалпы ортақ мысал
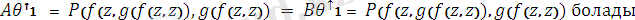
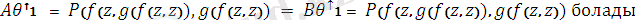
Ең жалпы унификаторды табу алгоритмі
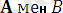
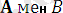 екі өрнек берілсін. Программада бұл өрнектердің алгоритмын компилятордың алгоритмдері төменде көрсетілген жағдайларда қарастырады.
екі өрнек берілсін. Программада бұл өрнектердің алгоритмын компилятордың алгоритмдері төменде көрсетілген жағдайларда қарастырады.

 горитмге кіруі:
горитмге кіруі:
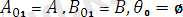
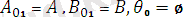
Мұнда берілген өрнектің алғашқы сұлбасы өз қалпында сақталып, ешқандай ауыстырулар орындылмайды. Алгоритым берілген өрнектердің күрделігі бойынша унификациялауды бастайды. Алгоритмның унификациялауды іздеу барысы:
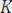
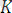 қадамда:
қадамда:

 астапқы өрнекке алғашқы ауыструды қолданғанда өрнектер денесінде сәйкессіздіктер жоқ болса, олар бірден унификацияланып ең жалпы унификатор, алғашқы ауыструдың өзі болады
.
Егер өрнектер құрамында сәйкессіздік болса, онда келесі қадамға өтеді.
астапқы өрнекке алғашқы ауыструды қолданғанда өрнектер денесінде сәйкессіздіктер жоқ болса, олар бірден унификацияланып ең жалпы унификатор, алғашқы ауыструдың өзі болады
.
Егер өрнектер құрамында сәйкессіздік болса, онда келесі қадамға өтеді.
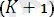
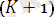 қадамда:
қадамда:

 , …,
, …,
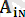
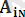 ;
;
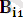
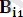 , …,
, …,
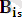
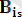 , …,
, …,
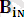
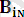 өрнектер денесінің әрбір элементінің көрінісі. Мұндағы i
өрнектер денесінің әрбір элементінің көрінісі. Мұндағы i

 қолданылған унификаторлардың реті, ал сандар өрнектер денсін құрайтын элементтердің реті.
қолданылған унификаторлардың реті, ал сандар өрнектер денсін құрайтын элементтердің реті.
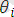
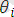 :
:
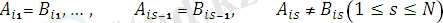
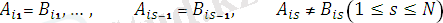 егер мұнда
егер мұнда

 жоқ болса(сәйкес емес элемент жоқ болса) онда
жоқ болса(сәйкес емес элемент жоқ болса) онда
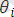
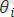 ең жалпы ортақ унификатор. Мұнда
ең жалпы ортақ унификатор. Мұнда
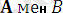
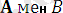 өрнектің құрамындағы екі элемент
өрнектің құрамындағы екі элемент
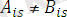
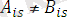 сәйкес емес болсын деп ұйғарым жасайық.
сәйкес емес болсын деп ұйғарым жасайық.
- термге тең болсын жәнеайнымалысы термге кімейтін болса, ондаенді жалпы тізбек, …, ;
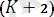
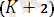 қадамда:
қадамда:
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz