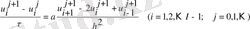Сызықты Навье-Стокс жүйесінің кері есебін шешудің параллель алгоритмі OpenMP негізінде


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 60 бет
Таңдаулыға:
Әл - Фараби АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ УНИВЕРСИТЕТІ
МЕХАНИКА-МАТЕМАТИКА ФАКУЛЬТЕТІ
МАГИСТРАТУРА
Информатика кафедрасы
МАГИСТРЛЫҚ ДИССЕРТАЦИЯ
СЫЗЫҚТЫ НАВЬЕ - СТОКС ЖҮЙЕСІ ҮШІН КЕРІ ЕСЕПТІҢ ШЕШІМІНІҢ АЛГОРИТМІН ПАРАЛЛЕЛЬДЕУ
(6M060200-«Информатика»)
Орындаушы Рыскелді. Н. Н "" 2013 ж.
Ғылыми жетекші
ф. -м. ғ. к., доцент Макашев Е. П. "" 2013 ж.
Қорғауға жіберілді
Кафедра меңгерушісі Урмашев Б. А. "" 2013 ж.
Алматы 2013
СЫЗЫҚТЫ НАВЬЕ - СТОКС ЖҮЙЕСІ ҮШІН КЕРІ ЕСЕПТІҢ ШЕШІМІНІҢ АЛГОРИТМІН ПАРАЛЛЕЛЬДЕУ
Түйін
Магистерлік жұмысқа кіреді: кіріспе, үш тараудан негізгі бөлім, қорытынды, қолданылған әдебиеттер тізімі.
Жұмыс 71 бет, 20 суреттен тұрады. Қолданылған әдебиеттер тізімінің саны-10.
Бұл магиcтерлік жұмыста сызықты Навье-Стокс жүйесі үшін кері есептің шешімінің алгоритмін параллелдеу қарастырылады. Кері есептің теориясы дифференциалдық теңдеулер үшін қарқынды дамып келе жатқан математикалық физиканың бір бөлігі болып табылады. Бұл зерттеудің маңыздылығы - көптеген математикалық әдістерді жасап өңдеуге комектеседі, және осы математикалық модельдер арқылы кең класты маңызды мәселелерді шешуге мүмкіндік береді. Мұндай маңызды мәселелерге геофизикада, биологияда, медицинада, экологияда, ортаны қорғау орталықтарында және термоядролық синтезді басқару және т. б. қолданады. Бұл жайт, әрине, заманауи математиканың өзекті мәселелеріне жатады.
Кері есептерді шешу үшін бір немесе бірнеше коэффициенттерді табу керек, сонымен қатар, дифференциалдық теңдеудің немесе дифференциалдық теңдеулер жүйесінің оң жағын, шектік маңайын, есепті шешу жайындағы қосымша мәліметтерге байланысты шектік немесе бастапқы шарттарды анықтау қажет болады.
Магистрлік жұмыстан алынған жаңа нәтижелерді келесідей атап айтуға болады:
- Сызықты Навье-Стокс жүйесі кері есептің жалпыланған шешімділігі дәлелденді;
- Сызықты Навье-Стокс жүйесі үшін кері есептің шекті-айырымдық айқын схемасы құрылды;
- Сызықты Навье-Стокс жүйесі үшін кері есептің бір өлшемді аналогының сандық мәні алынды;
- Сызықты Навье-Стокс жүйесі үшін кері есептің шешімінің алгоритмі OpenMP технологиясын пайдалану арқылы параллелденді;
- Параллелдеу барысында құрылған алгоритмнің орындалуы уақыт жағынан жоғарғы үнемділікке жетті.
Диссертация нәтижесінің апробациясы:
Рыскелді Н., Сызықты навье - стокс жүйесі үшін кері есептің шешімінің алгоритмін параллельдеу. // Математика, механика и информатика бойынша V Республикалық ғылыми-практикалық студенттік конференция. Баяндамалар жинағы (Астана, 5-6 сәуір, 2013г. )
РАССПАРАЛЛЕЛИВАНИЕ АЛГОРИТМА РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ ДЛЯ ЛИНЕАРИЗОВАННОЙ СИСТЕМЫ НАВЬЕ - СТОКС
Резюме
Магистерская работа включает в себя: введение, основную часть, состоящую из трех разделов, заключение, список использованных источников.
Работа состоит из 71 страниц, 20 рисунков. Список литературы содержит 8 наименования.
В этой магистерской работе рассматривается распараллеливание алгоритма решения обратной задачи для линеризованной системы Навье-Стокса. Теория обратных задач для дифференциальных уравнений является интенсивно развивающейся областью математической физики. Интенсивность исследований в этой области обусловлена необходимостью разработки математических методов решения обширного класса важных прикладных проблем. К этим проблемам относятся разнообразные задачи из самых разных отраслей науки, а именно в сейсмологии, геофизики, биологии, медицине контроле качества промышленных изделий, экологии, охране окружающей среды и управляемого термоядерного синтеза и т. д., что ставит их в ряд актуальнейших проблем современной математики.
В обратных задачах помимо решения требуется найти один или несколько коэффициентов, правых частей дифференциальных уравнений или системы дифференциальных уравнений, границ области, граничных или начальных условий по той или иной дополнительной информации о решениях уравнений.
В магистерской работе получены следующие результаты:
- Доказана обобщенная разрешимость обратной задачи для линеризованной системы Навье-Стокса;
- Построена гранично-разностная явная схема обратной задачи для линеризованной системы Навье-Стокса;
- Получена численное значение аналога одномерной обратной задачи для линеризованной системы Навье-Стокса;
- Исрользуя технологию OpenMP была распараллелина обратной задачи для линеризованной системы Навье-Стокса;
- В ходе распараллеливание построенный алгоритм при выполнении достиг высого результата по экономии времени.
Апробация диссертационных выводов:
Рыскелді Н., Расспараллеливание алгоритма решения обратной задачи для линеаризованной системы Навье - Стокс. // V Республиканская научно-практическая студенческая конференция по математике, механике и информатике. Сб. докладов. (Астана, 5-6 апреля, 2013г. )
PARALLEL ALGORITHM DESIGN FOR LINEAR NAVIE-STOCKS INVERSE PROBLEM
Summary
Master's work includes: introduction, main part, consisting of three sections, the conclusion, list of references.
The paper consists of 71 pages, 20 figures. References contains 8 items.
In this master's work the parallelization of the algorithm for solving the inverse problem for the linerizovannoy of the Navier-Stokes equations. The theory of inverse problems for partial differential equations is a rapidly developing field of mathematical physics. The intensity of research in this area is due to the need to develop mathematical methods for solving a broad class of important practical problems. These problems include a variety of tasks from different branches of science, namely the science of seismology, geophysics, biology, medicine, quality control of industrial products, ecology, environmental protection and controlled thermonuclear fusion, etc., that puts them in a number of urgent problems of modern mathematics.
In addition to solving inverse problems need to find one or more factors, the right-hand sides of differential equations or systems of differential equations, boundary area, the boundary or initial conditions for some more information about the solutions of the equations.
In the master's work with the following results:
- A generalization of the inverse problem for linerizovannoy the Navier-Stokes equations;
- Built-bound-difference scheme is a clear inverse linerizovannoy for the Navier-Stokes equations;
- We obtain the numerical value of the one-dimensional analogue of the inverse problem for linerizovannoy of the Navier-Stokes equations;
- Isrolzuya OpenMP technology was rasparallelina linerizovannoy inverse problem for the Navier-Stokes equations;
- During the parallelization of the algorithm built in the performance achieved High luminance of the time-saving;
Testing dissertation findings:
Ryskeldі N., Rassparallelivanie algorithm for solving the inverse problem for the linearized Navier - Stokes. / / V Republican scientific-practical conference of students in mathematics, mechanics and computer science. Sb. dokladov. (Astana, April 5-6, 2013. )
АНЫҚТАМАЛАР
ПЭЖ − Параллелді есептеуіш жүйелер
Абсолютті (сөзсіз) аппроксимация
− кез-келген заң бойынша ешбір шартсыз байланыспаудың
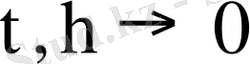 болғанда нөлге ұмтылатын аппроксимация түрін айтады
болғанда нөлге ұмтылатын аппроксимация түрін айтады
Параллель компьютер − жалпы міндеттерді шешуде бірігіп жұмыс істей алатын процессорлардың жиынтығы
Параллель программа - әр процесс өзiнiң жеке процессорында орындалатын программа, демек, процесс параллель орындалады
КПЕЖ − көп процессорлы есептеуіш жүйелер
Талдап тексеру дәрежесi - тоқталғанға дейiнгi немесе үзiлгенге дейiнгi элементар процессор орындайтын типтiк кодтар ағынынң ұзындығы
Басқарудың әртүрлiлiгi - басқару блогының өңделетiн элементке қатынасы және әдетте ол Флиннiң SIMD категориясында сипатталған компьютерлерге қолданылады
Желi диаметрi - кез-келген екi торап арасындағы ең ұзын жол
Масштабтау (scalability) - желiге қосылған торап санын өсiргенде байланыстың күрделiлiгi қаншалықты өсетiнiн бiлудi қажет ететiн қасиет
Баньян желiсi - ауыстырғыштары бар көпбаспалдақты желi, оның кiрiстер мен шығыстар саны бiрдей, iшкi тораптары mxm айырғыш болады
Open MP - компилятор директиваларының және көмекші программалар жиынтығы
НОРМАТИВТІ СІЛТЕМЕЛЕР
Ұсынылған диссертацияда келесі стандарттарғы сілтемелер қолданылған: ГОСТ 2. 111-68 Конструкторлық құжаттаманың біркелкі жүйесі. Нормоконтроль.
МС 7. 1-84 Ақпарат, кітапхана және баспа ісі бойынша стандарттар жүйесі. Құжаттың библиографиялық сипаттмасы. Құрастырудың жалпы талаптары мен ережелері.
МС 7. 9-95 (ИСО 214-76) Ақпарат, кітапхана және баспа ісі бойынша стандарттар жүйесі. Реферат және аңдатпа. Жалпы талаптар.
МС 7. 12-93 Ақпарат, кітапхана және баспа ісі бойынша стандарттар жүйесі. Библиографиялық жазба. Қысқартылған сөздер. Жалпы талаптар мен ережелер.
МС 7. 32-2001 Ақпарат, кітапхана және баспа ісі бойынша стандарттар жүйесі. Ғылыми-зерттеу жұмысы бойынша есеп беру. Ресімдеу құралы мен ережелері.
МС 7. 54-88 Ақпарат, кітапхана және баспа ісі бойынша стандарттар жүйесі. Ғылыми-техникалық құжаттар материалдарында және қасиеттер бойынша заттардың сандық деректерін көрсету. Жалпы талаптар.
МС 8. 417-81 Өлшемдер бірлігін қамтамасыз ететін мемлекеттік жүйе. Физикалық шама бірліктері.
МАЗМҰНЫ
КІРІСПЕ
Бұл жұмыста сызықты Навье-Стокс жүйесі үшін кері есептің шешімінің алгоритмін параллелдеу қарастырылады. Кері есептің теориясы дифференциалдық теңдеулер үшін қарқынды дамып келе жатқан математикалық физиканың бір бөлігі болып табылады. Бұл зерттеудің маңыздылығы - көптеген математикалық әдістерді жасап өңдеуге комектеседі, және осы математикалық модельдер арқылы кең класты маңызды мәселелерді шешуге мүмкіндік береді. Мұндай маңызды мәселелерге геофизикада, биологияда, медицинада, экологияда, ортаны қорғау орталықтарында және термоядролық синтезді басқару және т. б. қолданады. Бұл жайт, әрине, заманауи математиканың өзекті мәселелеріне жатады.
Кері есептерді шешу үшін бір немесе бірнеше коэффициенттерді табу керек, сонымен қатар, дифференциалдық теңдеудің немесе дифференциалдық теңдеулер жүйесінің оң жағын, шектік маңайын, есепті шешу жайындағы қосымша мәліметтерге байланысты шектік немесе бастапқы шарттарды анықтау қажет болады. Мысалы, физикалық денеде жылудың таралуын талқыласақ, тура есеп үшін объкттің шекті температурасын білу қажет, оның бастапқы анықталуын және әр мезетте уақытқа тәуелді жылудың таралуын анықтау керек. Кері есеп жағдайында осы параметрлердің ке-келгені белгілі болуы мүмкін. Осындай есептер үшін қойылымды дұрыс анықтау үшін модельдеу процесі барысында қосымша тағы мәлімет керек етеді, мысалыға, денеде температураның таралуы немесе жылудың таралу процесіндегі кейбір интегралдық характеристикалар болуы мүмкін. Мұндай қосымша мәліметтерді осы есеп үшін көбінесе “қайта анықталған” деп атайды.
Кері есептің негізгі теориясы келесі математиктердің жұмыстарында көрсетілген: А. Н. Тихонов, В. К. Иванов, М. М. Лаврентьев, П. С. Новиков, В. А. Марченко, И. М. Гельфанда, Б. И. Левитан, М. Г. Крейн, Л. Д. Фадеев, А. С. Алексеев, В. Г. Романова, А. И. Прилепко, Carleman T., Borg G., John F., Calderon A. P., Pucci C., Lions J. -L.
Дифференциалдық операторлардың тарылулары қисынды қисынды тарылулар теориясын кейбір нақты Стокс операторына қолданып алынған нәтижелер, сонымен қатар, гидро және газ динамикасының теңдеулерін зерттеу бағытындағы Навье-Стокс тектес есептердің шешімдеріне жасалған бағалаулар барлығының теориялық қызығушылығын тудырады.
Навье-Стокс теңдеуін өте дәл сипаттау үшін үлкен көлемдегі мәліметтерді өңдеу қажет. Бұл мақсатта параллельді есептеуіш жүйелерді қолданған тиімді. Параллелді есептеуіш жүйелерді қолдану (ПЭЖ) есептеу техникасының дамуының стратегиялық бағыты болып табылады. Қазіргі заманғы ғылым мен техника мүмкіндіктерінің "үлкен шақыру" мәселелері: климатты моделдеу, гендік инженерия, интегралдық схемаларды жобалау, қоршаған ортаның ластануының анализі, емдік дәрумендерді жасау және тағы сол сияқтылар - өздерінің анализі үшін әр секундта қалқымалы үтірі бар (1 TFlops) 1000 миллиард операцияларды орындайтын ЭЕМ талап етеді.
Компьютерлік архитектура мен желілік технологиялардың дамуы, сондай-ақ есептеудің орасан көп санын талап ететін жаңа, ғылыми және қолданбалы міндеттердің пайда болуы программалау мен есептеу технологияларында параллель есептеулердің көкейкестілігі мен болашағы бар екендігін көрсетіп, программалау мен есептеу технологияларындағы орталық орындардың бірінен орын алды.
Жоғарғы дәрежелелі өнімділікті есептеуіш жүйелерді құру мәселесі қазіргі заманғы ғылым мен техникалық есептердің ең күрделісі болып табылады. Осы мәселені шешу көптеген талантты ғалымдар мен конструкторлардың білімдері мен күштерін жан - жақты концентрациялағанда ғана мүмкін, оның үстіне ғылым мен техниканың соңғы жетістіктерін қолдануды және маңызды финанстік инвестицияларды талап етеді. Сонымен қатар осы саладағы соңғы кездегі жетістіктер таңқаларлықтай. "Компьютерлік белсенділікті стратегиялық шектеу" Accelerated Strategic Computing Initiative - ASCI) бағдарламасы АҚШ-та 1995ж қабылданған, осының негізінде суперЭЕМ- дердің өнімділігін 18 айда 3 есе арттыру және өнімділік дәрежесін секунтына 100 триллион операцияларды орындауға арттыру мәселелері болды. Қазіргі уақытта жылдам әрекет ететін суперЭЕМ-дердің бірі NEC жапон фирмасының бір векторлық процесстің жылдамдығы секундтына 8 миллиард (8 GFlops) операциялар орындайтын SX-6 компьютері болып табылады. Көп процессорлы жүйелер үшін қол жеткізілген жылдам әрекет ету көрсеткіштері әлде қайда жылдам: мысалға, Intel (США, 1997) фирмасының ASCI Red жүйесінің жылдамдығы секундтына 1, 8 триллион (1, 8 TFlops) операциялар. Осы курстың лекйияларын жазу кезіндегі жылдам әрекет етуші есептеуіш жүйелердің Top 500 тізімінде BlueGene/L есептеуіш комплексі алғашқы қатарда.
1 НЕГІЗГІ ТЕҢДЕУЛЕР ЖҮЙЕСІ
1. 1 Математикалық физиканың негізгі есептері
Қарапайым дифференциалдық теңдеудің шешімі бір айнымалыға
 және т. с. с. тәуелді болады. Көптеген тәжірибелік есептердің шешімі-ізделінетін функциялар бірнеше айнымалы және берілген мәліметтерге тәуелді теңдеулерге, ізделінетін функция есептері дербес туынды болады. Олар дербес туынды теңдеулер деп аталады.
және т. с. с. тәуелді болады. Көптеген тәжірибелік есептердің шешімі-ізделінетін функциялар бірнеше айнымалы және берілген мәліметтерге тәуелді теңдеулерге, ізделінетін функция есептері дербес туынды болады. Олар дербес туынды теңдеулер деп аталады.
Математикалық қойылымдар дифференциалдық теңдеулермен бірге кейбір қосымша шарттардан құралады. Егер шешім шектелген облыста ізделінсе, онда оның шекаралық шарттары беріледі, олар шекаралық (шектік) деп аталады. Осындай есептер шектік есептер деген атауға ие және дербес туынды теңдеулерге арналған.
Алғашқы шарттарды қанағаттандыратын мәндері берілген есеп дербес туынды теңдеулер жүйесі үшін Коши есебі (КЕ) деп аталады. Сол себепті есеп шығару барысында шексіз кеңістікте шығарылады және шекаралық шарттар берілмейді. Алғашқы және шекаралық шарттар қойылатын есептер стационарлық емес (аралас) шектік есептер деп аталады. Алынатын шешімдер уақыт өтуімен өзгереді.
Дұрыс қойылған есеп алғашқы және шекаралық шарттарын қанағаттандыратын шешімдері бар, сонымен қатар сол теңдеулердің шарттарының коэффициенттерінен үзіліссіз тәуелді болатын есептерді атайды.
Қарастырылып отырған облыстың түрлі сеткеларының енгізілуіне негізделген есептеу әдістерінің ішіндегі түрлі әдістерді қарастырайық. Барлық туынды, алғашқы және шекаралық шарттар байлам сеткаларының функция мәндері арқылы беріледі, соның нәтижесінде түрлі схема деп аталатын сызықтық теңдеулер жүйесі шығады. Сетканың қарастырылып жатқан облысқа енгізілуіне негізделген дербес туынды теңдеулер шешуіне байланысты түрлі сеткалар құрастырылады. Сеткалар байламдары есептелетін нүктелер болып табылады (1-сурет) .
1-сурет. Сеткалар байланымы.
a≤x≤b x i =a+ih 1 (I=0, 1, …, Ι)
c≤y≤d y j =c+jh 2 (j=0, 1, …, J)
Түрлі сеткаларды құрастыру үшін дербес туынды теңдеулер кейбір шаблондардың шектік түрлі қатынастарымен алмастырылады. Сонда ізделініп жатқан функцияның нақты мәндері U торлы функциясының мәндерімен u түрлі байлам сеткаларында алмастырылады.

Айырымдылық схемасы алғашқы және шекаралық шарттар жылу өткішгіштік теңдеулерін шешу үшін келесі түрде беріледі:
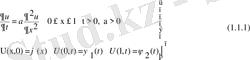
Кез-келген мезетте қарастырылып жатқан [0, 1] кесіндісінің аяғында ψ
1
(t) және ψ
2
(t) - температураларының бөлінуі алғашқы және шекаралық шарттарымен келісілген, яғни
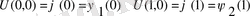 болуы керек. Тік бұрышты торды енгізейік :
болуы керек. Тік бұрышты торды енгізейік :
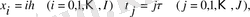 мұндағы һ, τ-қадамдар.
мұндағы һ, τ-қадамдар.
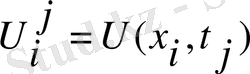 -сетканың байламдарындағы функцияның мәндері. Сондықтан,
-сетканың байламдарындағы функцияның мәндері. Сондықтан,
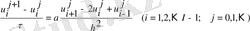
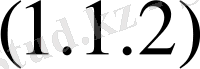
Торлы функцияның ішкі байламдарындағы мәндерін табу үшін алгебралық теңдеулер жүйесін табамыз. Шекаралық шарттан
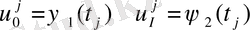 (
(
 4)
4)
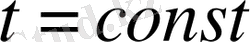 болғанда байламдар жиынтығы қабат деп аталады. (
болғанда байламдар жиынтығы қабат деп аталады. (
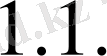 2) -ден тізбекті мәндерді
2) -ден тізбекті мәндерді
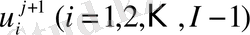 -нің
-нің
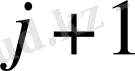 қабатына лайықты мәндер арқылы
қабатына лайықты мәндер арқылы
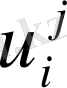 -ді
-ді
 -қабатында табамыз. Мұндай схемалар айқындалған деп аталады.
-қабатында табамыз. Мұндай схемалар айқындалған деп аталады.
 болғанда есеп басында бастапқы қабаттағы алғашқы шартпен анықталатын келесі түрдегі шешім қажет :
болғанда есеп басында бастапқы қабаттағы алғашқы шартпен анықталатын келесі түрдегі шешім қажет :
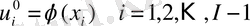 (
(
 5)
5)
Әрбір айырымдылық теңдеу (
 3) айқын схемаға қарағанда әрбір үш белгісіз нүктеде жаңа мағына қабатының мәндерін құрайды, сондықтан алдындағы қабаттың белгілі шешімдері арқылы бұл мәндерді лезде табуға болмайды. Олар айқынсыз схемалар деген атқа ие. Сонда (
3) айқын схемаға қарағанда әрбір үш белгісіз нүктеде жаңа мағына қабатының мәндерін құрайды, сондықтан алдындағы қабаттың белгілі шешімдері арқылы бұл мәндерді лезде табуға болмайды. Олар айқынсыз схемалар деген атқа ие. Сонда (
 3) айырымдық схема сызықтық үш нүктелік теңдеулерден құралады, бірақ әрбір теңдеу тап осы қабаттың үш нүктесіндегі белгісіз функциядан тұрады. Ол айдап шығу әдісімен шешіледі.
3) айырымдық схема сызықтық үш нүктелік теңдеулерден құралады, бірақ әрбір теңдеу тап осы қабаттың үш нүктесіндегі белгісіз функциядан тұрады. Ол айдап шығу әдісімен шешіледі.
Тап осы мысалда екі қабатты схеманы қарастырдық, яғни әрбір айырымдылық теңдеуге екі қабатты функция мәндері -төменгі, қайсыда шешімі табылған және жоғарғы, байламдағы шешімдері ізделуде кіреді.
Жинақтылық. Аппроксимация. Орнықтылық.
Алғашқы және шекаралық шарттары берілген дифференциалдық есеп дербес туынды теңдеулермен операторлық түрде құрастырылып жазылады.
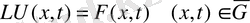 (
(
 6)
6)
Операторлық теңдеу негізгі дербес туынды теңдеу және қосымша алғашқы және шекаралық шарттарынан тұратын теңдеуден құралады.
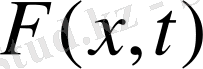 теңдеудің алғашқы және шекаралық шарттарының оң жағын бейнелейді,
теңдеудің алғашқы және шекаралық шарттарының оң жағын бейнелейді,
 есептеу облысынан да, шекарадан да тұрады. (
есептеу облысынан да, шекарадан да тұрады. (
 6) дифференциалдық есепті айырымдылық есебімен алмастырамыз, мұндағы
6) дифференциалдық есепті айырымдылық есебімен алмастырамыз, мұндағы
 , мұндағы
, мұндағы
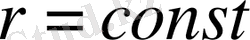 .
.
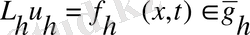 (
(
 7)
7)
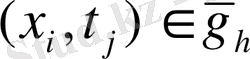 сеткалар байламдарында
сеткалар байламдарында
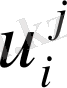 торлар функциясының мәнін ізделінетін
торлар функциясының мәнін ізделінетін
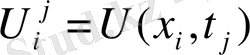 функцияның мәндерін жуықтап сол байламдағы қателіктермен алмастырады.
функцияның мәндерін жуықтап сол байламдағы қателіктермен алмастырады.
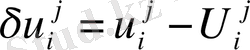 . (
. (
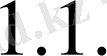 8)
8)
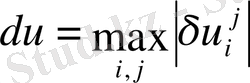 енгіземіз.
енгіземіз.
Егер
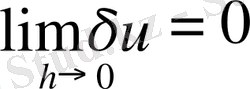 (
(
 9) байламдар торлары қоюланса, яғни бұл қателіктер мәндері нөлге ұмтылады, олай болса айырымдылық схема (
9) байламдар торлары қоюланса, яғни бұл қателіктер мәндері нөлге ұмтылады, олай болса айырымдылық схема (
 7) қосылатын деп аталады.
7) қосылатын деп аталады.
Егер
 мұндағы
мұндағы
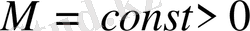 , онда айырымдылық схемасы k-шы дәлдік ретті немесе
, онда айырымдылық схемасы k-шы дәлдік ретті немесе
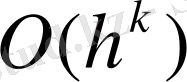 жылдамдығымен қосылады деп те айтады. Тордағы қателікті есептеу үшін
жылдамдығымен қосылады деп те айтады. Тордағы қателікті есептеу үшін
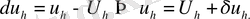 (
(
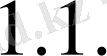 7) теңдеуін жазайық. (
7) теңдеуін жазайық. (
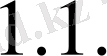 7) -ге қойып,
7) -ге қойып,
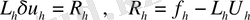 (
(
 10) аламыз.
10) аламыз.
Айырымдылық схеманың
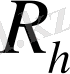 өлшемі байланыспау деп аталады (аппроксимация қателігі) . Өлшемдік сипаттамасын енгізейік.
өлшемі байланыспау деп аталады (аппроксимация қателігі) . Өлшемдік сипаттамасын енгізейік.
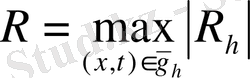 (
(
 11)
11)
 болғанда аппроксимация һ-пен салыстырғанда k-ші ретті болады. (
болғанда аппроксимация һ-пен салыстырғанда k-ші ретті болады. (
 7) айырымдылық схема (
7) айырымдылық схема (
 6) негізгі дифференциалдық есепті аппроксимациялайды, егер
6) негізгі дифференциалдық есепті аппроксимациялайды, егер
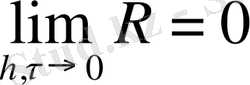 (
(
 12)
12)
яғни, торды ұсақтаса онда байланыспау нөлге ұмтылады.
Абсолютті (сөзсіз) аппроксимация кез-келген заң бойынша ешбір шартсыз байланыспаудың
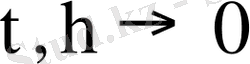 болғанда нөлге ұмтылатын аппроксимация түрін айтады. Шартты аппроксимацияда кеңістік және уақыт бойынша қадамдар өлшемдеріне кейбір шарттар қойылады. (
болғанда нөлге ұмтылатын аппроксимация түрін айтады. Шартты аппроксимацияда кеңістік және уақыт бойынша қадамдар өлшемдеріне кейбір шарттар қойылады. (
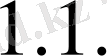 7) айырымдылық схемасы орнықтылықтанған деп аталады, егер оның шешімі кіретін мәліметтермен үзіліссіз байланыста болса, яғни кіретін мәліметтер шамалы аз өзгерсе соған сай шешімнің мәндері де аздап өзгереді. Орнықтылық айырымдылық схемасының түрлі қателіктерге сезімталдығын сипаттайды.
7) айырымдылық схемасы орнықтылықтанған деп аталады, егер оның шешімі кіретін мәліметтермен үзіліссіз байланыста болса, яғни кіретін мәліметтер шамалы аз өзгерсе соған сай шешімнің мәндері де аздап өзгереді. Орнықтылық айырымдылық схемасының түрлі қателіктерге сезімталдығын сипаттайды.
Теорема:
Егер (
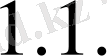 6) негізгі дифференциалдық есептің шешімі бар болса, ал (
6) негізгі дифференциалдық есептің шешімі бар болса, ал (
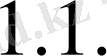 7) айырымдылық схемасы берілген (
7) айырымдылық схемасы берілген (
 6) шешімді орнықтылайды және аппроксициялайды, сонда айырымдылық шешімі дәлдікке қосылады.
6) шешімді орнықтылайды және аппроксициялайды, сонда айырымдылық шешімі дәлдікке қосылады.
1. 2 Параболалық типті айырымдылық схемалары
Параболалық типті теңдеудің классикалық мысалы жылу өткізгіштің теңдеуі болып табылады(диффузияя) . Біртекті кеңістікте біртекті (энергия көзінсіз) жылу өткізгіштіктің теңдеуі мынандай түрде болады
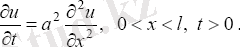 (1. 2. 1)
(1. 2. 1)
Егер де шекараларда х= 0 және х=l функцияның ізделінетін мәні мына u(x, t) түрде берілсе,
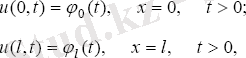 (1. 2. 2)
(1. 2. 2)
Яғни бірінші тектің шекаралык шарттары және одан баска, алғашқы шарттары берілген
u(x, 0) = ψ (x), 0≤ x ≤ l, t= 0 , (1. 2. 4)
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz