Ақпараттық модель және оның берілу жолдары

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 53 бет
Таңдаулыға:

Мазмұны

Беті

Кіріспе . . . 3

І . Ақпараттық модель және оның берілу жолдары

1. 1. Ақпараттың формула түрінде берілуі . . . 5

1. 2. Мәліметтердің кесте түріндегі көрінісі . . . 14

1. 3. Ақпараттың граф түріндегі көрінісі . . . 23

ІІ. Ақпараттық модель ретіндегі алгоритмдер мен

программалар

2. 1. Ақпараттық модельдеудің басқа да түрлері . . . 36

2. 2. Алгоритмді орындау қызметіндегі ақпараттық модель . . . 40

2. 3. Бір тапсырманың әртүрлі моделі . . . 48

Қорытынды . . . 55

Пайдаланылған әдебиеттер тізімі . . . 56

Қосымша А . . . 57

Қосымша В . . . 60

Кіріспе

Модель (латынның ”modu lus”- өлшем, үлгі, мөлшер) - бұл қандай да бір объект сипатының, көрінісінің бейнесі. Адамдар модель құру кезінде объектілердің маңызды қасиеттерін көрсетуге тырысады да, маңызды емес жағын мүмкіндігінше қарастырмайды. Мысалы: глобуста-мұхиттар мен теңіздер, материктер мен үлкен аралдар көрсетіледі, ал кішкене өзендер мен аралдар оған түспей қалады.

Информатика сабағын оқыту кезінде бізді ақпараттық модельдер, яғни ақпараттық процестерге қатысы бар модельдер қызықтырады. Біріншіден, бәрімізге белгілі ақпарат-бұл материалдық емес категорияға жатады, сондықтан ақпараттық модель абстрактылы болады.

Екіншіден ақпараттық модельдер таңба түрінде берілуі қажет. Себебі хабарлар таңба түрінде болады. Таңбалық модельдерді математикалық және ақпараттық модельдер деп бөлу қабылданған.

Ақпараттық модель - ақпараттық процестерді сипаттайтын модель немесе объектілер, процестер, құбылыстар қасиеттері мен жағдайлары туралы ақпараттардан тұратын модель. Ақпараттық модельдің қарапайым мысалдары болып объектілердің қасиеттерін сипаттау арқылы атын табуға болатын түрлі жұмбақтарды айтуымызға болады (қысы-жазы бір түсте, қолы жоқ сурет салады) . Ақпараттық модельге анықтамалық басылымдар. Энциклопедиялар мәтіндерін жатқызуымызға болады.

Егер модель компьютерде өңделіп құралатын болса, онда оны компьютерлік деп атайды. Компьютерлік модель - бұл программалық құралдар көмегімен жүзеге асатын модель.

Компьютерде қандай да бір формулалар бойынша есептеулер орындалса, онда бұл жағдайда біз математикалық, компьютерлік модельдеу туралы айтылып жатыр деп түсінуімізге болады. Компьютерлік өңдеу қажет емес барлық модельдер компьютерлік емес модельге жатады. Мысалы: біз есепті дәптерде шешу кезінде компьютерлік емес математикалық модельмен жұмыс істейміз.

Көбінесе компьютерлік модельдердің модельмен жұмыс кезінде қолданатын программалық қамсыздандыру бойынша ажыратуға болады.

Компьютерлік модельдерді өңдеу үшін қолданылып жүрген программалық жабдықтар (математикалық пакеттер, электрондық кесте-лер, графикалық редактор және т. б. ) пайдаланылады немесе программалау тілдері (Бейсик, Паскаль, С+ + және т. б. ) көмегімен программалар жасалынады.

Бастапқыда модель деп анықталған жағдайда объектіні алмастыратын қандай да бір көмекші объекті аталған. Сондықтан табиғат заңдылығының әмбебаптығы модельдеудің жалпылығы және біздің білімдерімізді модель түрінде бейнелеудің мүмкіндіктері сәйкессіз болады. Мысалы ертедегі философтар табиғи процестерді модельдеу мүмкін емес, табиғи және жасанды процестер түрлі заңдылықтарға бағынады деп санады. Олар табиғатты тек қана логиканың, талқылау әдістерінің, пікір алмасулардың, яғни замандық технологиялардың, тілдік модельдеудің көмегімен бейнелеуге болады деп жобалады. Ұзақ уақыттар бойына ” Модель ” түсінігі арнайы типтегі материалдық объектілерге ғана, мысалы: маникен (адам денесінің моделі), плотинаның кішірейтілген гидродинамикалық моделі, кемелер мен самолёттердің, жануарлардың модельдері ретінде қалыптасты.

Уақыт өте келе нақты объектілер жасанды сызбалардың, суреттердің, карталардың модельдік ерекшеліктері арқылы сипаттала бастады. Келесі қадамда модель ретінде нақты объект ғана емес абстрактылы, идеалдық құрылымдардың да жұмыс істеу мүмкіндіктері белгілі болады. Мұның мысалы математикалық модельдер бола алады. Математика негіздерін зерттеумен айналысатын математиктер мен философтардың еңбектерінің нәтижесінде модельдер теориясы жасалды. Онда модель бір абстрактылы математикалық құрылымның басқасына бейнелену, түрлендіру нәтижесі болып анықталады

Бастапқыда ақпараттық, кибернетикалық бағыттарды ғылыми пәндер аясында, содан соң ғылымның басқа да салаларында түрлі тәсілдермен іске асырылатын модель ретінде таниды. Негізінде модель білімнің мәнін нақтылау тәсілі ретінде қарастырылды.

Модель (Model Simulator) -

Қасиеттері белгілі бір мағынадағы жүйенің немесе процестің қасиеттеріне ұқсас объектілер немесе процестер жүйесі.
Сериялы бұйымдарды жаппай өндіруге арналған үлгі, эталон: кез келген бір объекті жұмысы, мысалы, процессордың жұмыс істеуін модельдейтін программа немесе құрылғы. Ол материалдық объект түрінде, математикалық байланыстар жүйесі ретінде немесе құрылымды имитацияланатын программа күйінде құрастырылады да, қарастырылатын объектінің жұмыс істеуін зерттеу үшін қолданылады.

Модельге қойылатын негізгі талап - оның қасиеттерінің негізгі объектіге сәйкес келуі, яғни пара-парлығы.

Модельдеу (моделирование: Simulation) - кез келген құбылыстардың, процестердің немесе объект жүйесінің қасиеттері мен сипаттамаларын зерттеу үшін олардың үлгісін құру және талдау; бар немесе жаңадан құрастырылған объектінің сипатын анықтау немесе айқындау үшін олардың аналогтарында (моделіне) объектілердің әр түрлі табиғатын зерттеу әдісі.

“Модель” түсінігі кибернетикада бақыланатын объектілер класын сипаттайтын теориялық моделін белгілеуде жиі қолданылады. Демек, кибернетикада берілген нақты объектінің моделі осы объект туралы теорияның моделі болып табылады. Компьютерлік модельдеу - бұл да оқып үйренетін объект теориясының модельденуі.

Модельденуші (модель субъектісі) - тек адам бола алады. Модельдеу объектісі табиғи (өсімдік, күн системасы) және адамның ықпалымен құрылып жасанды болуы мүмкін.

І. Ақпараттық модель және оның берілу жолдары

1. 1. Ақпараттың формула түрінде берілуі

Мектеп кезіндегі формула жиі кездесетін пәндерді еске түсірейік. Ең бірінші арифметика, алгебра, геометрия, физика пәндері есімізге түседі. Бұл кездескен формулалар математикалық формулалар деп аталады. Олар ақпараттың берілу түрлеріне қарай қолданылады: математикалық есептердің шартына қарай, физикалық заңдылықтар, заңға сыйымды физикалық, экономикалық, әлеуметтік жүйелердің және т. б. даму заңдылықтарына қарай қолданылады.

Математикада формула (латынның formula-форма, ереже, алдын-ала жазып қою) ұсыныстарды білдіруге арналған математикалық белгілердің қатынасы ретінде анықталады.

Мысалы, формуланың мәнін келесі өрнектерден қарайық:

2*2=4; x ³ +z ² <n; 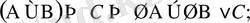2x2=5; y’=y; Бұл жерде барлығы математикалық мағынада жазылған, яғни “+” белгісі, арифметикадағы қосу амалын, “=” белгісі, теңдік амалды және т. б. білдіреді.

Мысалы,

Ньютон Биномы, n=3 болғанда:

(1+х) ³ = 1+3х+3x ² +x ³ .

Шеңбердің радиусының ұзындығы r: c=2 r.

Ом заңы: I=U/R, мұнда R-кедергі, U-кернеу, I-ток күші.

Экономикада, статистикада процестер мен құбылыстарды жазу үшін көбінесе математикалық формулалар қолданылады.

Мысалы,

n жыл ішіндегі p%-пен банкке салынған және қосылуы жылына m рет болса, S сом салым мөлшерін анықтау үшін, келесі формуланы қолдану керек:

BS=S(1+p/m/100) ^n*m 7

2000 жылдың бірінші жартысындағы кәсіпорынға түсетін ай сайынғы кірісті есептеу үшін келесі формула қолданылады:

Sp= ,

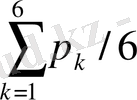Мұнда 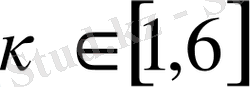- ай нөмірі, p _k - k айдағы кіріс.

Математикалық формуладан басқа химиялық формулалар: зат және химиялық реакциялардың формулалары белгілі. Бұларда “+” белгісі химиялық заттардың әсерлесуін, ал “=” белгісі, осы заттардың әсерлесуінен нәтиже шығатынын көрсетеді.

Мысалы,

Натрий гидроксиді мен тұз қышқылының өзара әсерлесуінен натрий хлориді және су пайда болады.

Жазылу реті:

HCl+NaOH=NaCl+H ₂ O.

Мұндай реакциялар иондық реакциялар деп аталады. Кейде оларды қысқартылған иондық теңдеу көмегімен жазуға болады.

Қысқартылған (ықшамдалған) иондық теңдеу бұл жағдайда:

H ⁺ +OH ^- = H ₂ O

болады.

Байқасақ, бұл жерде “+” белгісі екі түрлі мағынада қолданылып тұр, яғни біріншісі сутегі ионының “оң” екенін, екіншісі екі ионның қосылуын білдіреді.

Сонымен қатар формуланы таза гуманитарлық ғылымдарда, әдебиеттерде, тарихтарда, психологияларда кездестіреміз.

Мысалы,

Психологияда жеке тұлғаның өзін-өзі бағалауы туралы формуласы белгілі (Джемс, 1890) :

өзін-өзі бағалау = жетістік/талпыныс,

мұнда бөлу белгісі арифметикалық мағынадағы бөлуді білдірмейді. Мағынасына қарай, өзара байланысты үш объектілердің арасындағы қарым-қатынасты білдіреді.

Бұл формуланы талдай келе, біз Джемстің өзін-өзі бағалаудың екі жолын факт түрінде көрсеткенін көреміз. Шынында да, адам өзі туралы жоғары дәрежеде ойлауға мүмкіндігі бар.

Джемс: “ біз бұл өмірде өзімізді сезінуіміз, кім болғымыз келеді және не істегіміз келеді соған байланысты”.

Ақпараттың басқаша берілу түрлерінен формуланың негізгі айырмашылығы, ақпарат өте жинақы беріледі. Формулаларда барлық белгілердің өзіндік мағынасы бар, мысалы а ² және а ₂ .

Математикалық формулалардың құрылу этаптары және қасиеттерін келесі мысалдардан көреміз.

Мысалы,

Тікбұрышты үшбұрыштың қабырғаларының арақатынас моделіне, Пифагор теоремасы жатады: катеттерінің квадраттарының қосындысы гипотенузаның квадратына тең. Бұл жерде катеттер - үшбұрыштың тік бұрышына іргелес жатқан қабырғалары, ал гипотенуза - тік бұрышына қарсы жатқан қабырғасы.

Осы модельді көрсету үшін:

теоремадағы (есептегі) мәні берілген элементтерді бөлу; 2) оларды белгілеу (ғылыми тіл ретінде латын және гек әріптері қабылданған, Ежелгі Грецияның ғалымдары европалық математиканың негізін қалаушылары болып саналады) ;

белгіленген элементтердің қандай қарым-қатынаста тұрғанын және бұл қатынастарға қандай математикалық операциялар сәйкес келетінін көрсету (орнату) ; белгіленген және берілген элементтердің қатынасын математикалық символдармен жазу қажет. Енді, тікбұрышты үшбұрыштың элементтеріне, теоремадағы қабырғалары (катеттер мен гипотенуза) және олардың ұзындықтары, үшбұрыштың бұрыштары және олардың өлшемі жатады. Формулаға катеттері мен гипотенузаның ұзындықтары берілсе жеткілікті.

Катеттерінің ұзындықтарын - а және b әрпімен, гипотенузаның ұзындығын - с әрпімен белгілеу қабылданған.

Мұндай белгіленулер былай жазылады:

а ² + b ² = с ² .

Бұл жерде а ² - ң өзі бірдей екі а санының көбейтіндісінің моделі болып табылады, яғни Пифагор теоремасын былай жазуға болады:

а*а + b*b = с*с.

Егер де катеттерінің белгіленулерін g және r әріптеріне, ал гипотенузасын q әрпімен белгілесек, онда Пифагор теоремасының формуласы өзгешелеу болады:

g ² + r ² = q ² ,

бірақ мазмұны жоғарыда айтылғандай болады.

Математикалық модельдеуден басқа, химияда, лингвистикада, әдебиетте, логикада (бірақ та бұл ғылымдарда ақпаратты модельдеу сурет, схема, кесте, алгоритм ретінде беріледі) формулалар кездеседі.

Мысалы,

Химиялық қосылулардың формуласын құруда формализацияның келесі тәсілдері кездеседі:

Әсерлесуге (қосылуға) түсетін элементтердің химиялық белгілерін қатарға жазу: а) Al O ; б) Na O ;

Д. И. Менделеевтің элементтердің периодты жүйе кестесіндегі осы элементтерге сәйкес келетін валенттілігін қою: III II I II

а) б)

Al O ; Na O ;

Осы сандардың ең кіші ортақ еселігін табу: (6) (2)

а) III II б) I II

Al O ; Na O ;

Ең кіші ортақ еселігін валенттілікке бөлу арқылы индексті анықтау: (6) (2)

а) III II б) I II

Al ₂ O ₂ ; Na ₂ O ₂ ;

Формулалар не үшін қажет?

Есептер формулада өте жинақы және себеп - салдар байланысы арқылы беріледі.

Мысалы,

Егер тікбұрышты үшбұрыштың а катеті, өзгермелі [t ₁ , t ₂ ] интервалындағы кез келген мәнді қабылдайтын болып және b катеті тұрақты болса, онда с гипотенузасы а катеттерінің ұзындығына байланысты функция болып табылады.

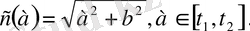
Бұл жағдайда с гипотенузасының ұзындығы а катетінің ұзындығына тәуелді болады, яғни олардың араларында себеп-салдар байланысы бар және формуладан бұл байланыс анық көрініп тұрады. Бұл тәуелділіктің шағын түрін кесте арқылы көрсетуге болады:

а катетінің ұзындығы: а катетінің ұзындығы

b=3 болғандағы с гипотенузасының ұзындығы: b=3 болғандағы с гипотенузасының ұзындығы

а катетінің ұзындығы: 1

b=3 болғандағы с гипотенузасының ұзындығы: 3, 16

а катетінің ұзындығы: 4

b=3 болғандағы с гипотенузасының ұзындығы: 5

а катетінің ұзындығы: 7

b=3 болғандағы с гипотенузасының ұзындығы: 7, 62

а катетінің ұзындығы: 10

b=3 болғандағы с гипотенузасының ұзындығы: 10, 44

Физикада, егер объектіге ықпал (әсер) ету белгілі болса, онда осы физикалық құбылыстарды және олардың орналасу тәртібін математикалық модельдің себеп-салдар байланысы арқылы дәлелдеуге болады.

Мысалы,

Үшбұрышты қарастырамыз. Үшбұрыштың бір қабырғасының ұзындығы қалған екі қабырғасының ұзындықтарының қосындысынан артық болмау керек деген бекіту бар. Бұл бекітудің формуласы мынадай:

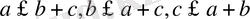Бұл жерде себеп-салдар байланысы жоқ. Формулалар кез келген үшбұрыштардың қабырғаларына арналған қатынас. Формулалар, объектілердің қасиеттерін басқа амалдармен сипаттауға болмайтындай көрсетеді, мысалы, шексіздік қасиеті.

Мысалы,

Функция, кесте, график, формула түрінде берілуі мүмкін.

y=(x+2) ² -3 функциясын қарастырайық.

х: х

у: у

х: -5

у: 6

-4 1

-3 -2

-2 -3

-1 -2

0 1

1 6

2 13

3 22

4 33

1. 1. 1. сурет. Функцияның кестелік түрде берілуі және графигі.

Кестеде мәннің тек қана соңғы санын беруге болады. Функция графигі шектелген аймағы туралы көрініс береді. Осы кемшіліктерге байланысты функцияның формулалық тапсырмалары еркін түрде беріледі. Сіз х-ті (сәйкесінше у-ті) кез келген үлкен немесе ең кіші деп елестете аласыз.

Уақыт өте келе әлемнің барлық құбылыстарынан себеп-салдар байланысын табуға болмайтыны туралы анықталды, бірақ формула өте ыңғайлы сипаттау болып қала берді. Сондықтан, функциялық тәуелділікті ғана емес, сонымен қатар әртүрлі детерминитикалық емес құбылыстарды да сипаттайтын формула пайда болды.

Мысалы,

Математикалық формулалар, ережеге сәйкес нақты физикалық, экономикалық, әлеуметтік жүйелерді зерттеудегі нәтижелері ретінде пайда болды. Бұл жағдайда олардың негізгі міндеті - байқау кезінде жүйелердің тәртібі мен қасиеттерін анықтау.

Математик - ғалымдар бірнеше мыңдаған жылдар бойы математикалық модельдеудің әдістерін жасап жатыр. Көптеген амалдар, тәсілдер, әдістер, математикалық модельдерді құрудың ұсыныстары жасалды.

Ақпараттық модельдің формула түрінде берілуін, әр түрлі білім саласында математика, физика, химия, экономика, статистика, логика салаларында кездестіреміз.

Ақпараттың басқаша берілу түрлерінен формуланың айырмашылығы, мұнда ақпарат көбінесе жинақы түрде беріледі. Формулаларда әр белгі ғана емес, сонымен қатар олардың байланысып орналасу ретінің де мағыналық жүктемесі болады.

Ғылымда ақпараттық модельдің көп таралған түрі - математикалық модель болып табылады.

Математикалық модель - әлемнің әр түрлі құбылыстарын, математикалық символдар көмегімен бейнелеу.

Математикалық формулалар, ереже, физикалық, экономикалық, әлеуметтік жүйелерді зерттеудегі нәтижелері ретінде пайда болды. Бұл жағдайда олардың негізгі міндеті - байқау кезінде жүйелердің тәртібі мен қасиеттерін анықтау.

Математикалық модельді құрудың іріленген кезеңдері:

теоремадағы (есептегі) мәні берілген элементтерді бөлу; оларды белгілеу (ғылыми тіл ретінде латын және грек әріптері қабылданған, Ежелгі Грецияның ғалымдары европалық математиканың негізін қалаушылары болып саналады) ; белгіленген элементтердің қандай қарым-қатынаста тұрғанын және бұл қатынастарға қандай математикалық операциялар сәйкес келетінін көрсету (орнату) ; белгіленген және берілген элементтердің қатынасын математикалық символдармен жазу. Формулаларды қолдану кезінде келесі айтылғандар рұқсат етіледі:

объектіні жинақты түрде бейнелеуге; физикалық құбылыстардың себеп-салдар байланысын бейнелеуге; объектіге басқа амалдармен сипаттауға болмайтын, мысалы, шексіздік қасиетін беруге; модельденетін объектілердің байқау кезіндегі қасиеті мен тәртібін айқындауға болады. Математикалық модельдеу - әлемнің сыртқы түрін танудағы қуатты әдістеме, болжау және басқару.

Математикалық модельдің талдауымен құбылыстардың мәнін анықтауға болады. Бұл математикалық модельдің ғылымда кең таралуы және практикалық әрекеттері ақпараттық модельдің қатарында ерекше орын алады.

Ақпараттың формула түрінде берілуіне тапсырмалар

Тапсырма 1

Келесі есептердің шешіміне математикалық модель құрыңыз және шарттардың формализациясын сипаттаңыз.

Есеп

Тауардың бағасы екі есеге сол процентпен көбейді. Егер бастапқы бағасы - 6000 сом, ал соңғысы - 6615 сом болса, онда әр кезде тауардың бағасы қанша процентке өсті?

Жауабы

Шартқа қатысты элементтері: бастапқы бағасы (СР деп белгілейміз), өсу проценті (р) , ақырғы бағасы (СО) . Олардың араларындағы байланысты математикалық символдардың көмегімен былай жазуға болады: СО = СР(1+р/100) ² .

Тапсырма 2

Алдыңғы есеп 9 сыныпқа арналған алгебра оқулығынан алынған, ал келесі есеп 2 сыныпқа арналған математика оқулығынан алынған. Осы есептің моделін құрайық.

Хоттабыч қарияның жасы әр түрлі цифрдан тұратын сандармен берілген.

Бізге белгілісі:

егер бірінші және соңғы санды өшіргенде, қосындысы 13-ке тең ең үлкен екіөлшемді сан шығады; бірінші сан соңғы саннан 4 есе артық. Хоттабыч неше жаста?

Жауабы

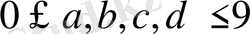Equation. 3 мұнда Equation. 3

b+c=13, bc=max(xy), x+y=13

a=4d.

Тапсырма 3

Физика курсының есептерін шешудегі формализация этаптарын жазайық.

Есеп

Спортшы секіру кезінде 2м биіктіктен секірді. Ол 2м биіктіктегі трибунаға сатымен көтерілді. Осы екі жағдайда ол бірдей қуат жіберді ме?

Жауабы

Есептің шартына қарап, биіктік пен қуаттың өзара байланысын анықтау керек. Есепті шешу үшін биіктікке көтерілуге кеткен уақыт қажет.

Есепті шешуге қажет формулалар:

а) қуатты табу үшін - жұмыс пен уақыттың қатынасы қажет: P=A/t;

б) денеге түскен күш пен жүріп өткен жолдың көбейтіндісі жұмысты береді. A=F*S;

в) дененің массасы мен үдеуінің көбейтіндісі күшті береді: F=mg;

Биіктікке көтерілуге кеткен уақыттан басқасы, екі жағдайда да бірдей болады. Берілген биіктікке көтерілуге кеткен уақыт пен қуаттың байланысын қарастырамыз. Қуат пен уақыттың тәуелділігі қайтымды пропорциональды, көтерілуге кеткен уақыт неғұрлым аз болса қуат соғұрлым көп болады. Зерттей келе, спортшының сатымен көтерілгендегі қуатына қарағанда, секірген кездегі қуаты үлкен.

Тапсырма 6

Информатика немесе алгебра курсындағы логика бөлімін еске түсіріп, келесі есептің формасын жасайық.

Есеп

Жүгіру жарысына түспес бұрын A, B, C, D-лар болжамдады:

A: жеңісті B алады;

B: D соңғы орынды алады;

C: А үшінші орынды алады;

D: А-ң болжамы орындалады.

Болжамдардың ішінен, жеңімпаздың болжамы дұрыс болып шықты. A, B, C, D-лардың орналасу реті қалай болады?

Жауабы

Келесі белгілеулерді енгіземіз:

А - А-ң болжамы орындалады;

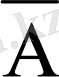Equation. 3 - А-ң болжамы орындалмайды;

А1 - А бірінші орынға ие болады;

Equation. 3 - А бірінші орынға ие болмайды.

Басқа жарысқа қатысушылардың иеленген орындары ұқсас.

Жасалған болжамдардың ішінен жеңімпаздың жауабы дұрыс болды, бұл біздің шартымыз, енді оны формулаға айналдыру былай болады: А жеңімпаз болды және оның болжамы дұрыс, ал B, C, D болжамдары дұрыс емес немесе B жеңімпаз болды және оның болжамы дұрыс, ал A, C, D болжамдары дұрыс емес және т. с. с.

Формуланың логика түрінде жазылуы:

Equation. 3 A, B, C, D-лардың орнына өздерінің болжамдарын қойсақ, есептің шартын қанағаттандыратын формула аламыз.

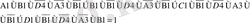Equation. 3

Қарастырған мәселелеміз бойынша ой-өрісімізді кеңейтейік!

Программалау барысында формулаларды көбінесе өрнектер деп атайды. Көптеген тілдерде пограммалауды жақындатылған математикалық жазбаларға жақындау етіп жазады, бірақ оның ерекше ережелері де бар: мысалы:

өрнек тек бір жолға ғана жазылуы мүмкін; тек жай жақшалар ғана қолданылуы мүмкін; операция белгілерін тастап кетуге болмайды; бөлу операциясына мына белгі қолданылуы керек «/», көбейту үшін «*», дәрежені көрсету үшін «^» (егер бұл белгілер арнайы бір тілде анықталған болса) ; функция аргументтері міндетті түрде жақшамен аяқталуы керек. Бірақ арифметикалық операциялар қарапайым түрде жазылады.

<операнд> <операция белгісі> <операнд>

Мысалы:

у:=(sqrt(x/2+5) -4*t-8) /x/t;

аналогты математикалық формула түрінде.

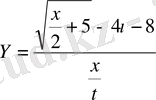Сонымен қатар есептеу алдындағы өрнектің поляк жазбасы программалау барысында кең таралған. Поляк деп аталатын себебі, оны поляк философы Я. Лукасевич (1878-1956 ж. ж. ) бірінші болып енгізді және символикалық логика формуласын пайдаланды.

Поляк жазбасының бір түрі кері поляк жазбасы болып табылады, оны келесі схема түрінде беруімізге болады.

<операнд> <операнд > <операция>

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.