Көпөлшемді көпбайланысты автоматты басқару жүйесін жобалау: модальды реттегіш, тиімді дискретті бақылаушы және агрегативті салыстыру жүйесін синтездеу


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 29 бет
Таңдаулыға:
ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНИСТРЛІГІ
Қ. И. СӘТБАЕВ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ ТЕХНИКАЛЫҚ УНИВЕРСИТЕТІ
Автоматика және Телемеханика кафедрасы
КУРСТЫҚ ЖОБА
Жоба тақырыбы: Автоматты басқару жүйесін жобалау.
Алматы 200
МАЗМҰНЫ
Курстық жобаға берілетін бастапқы мәліметтер . . . 3
Кіріспе . . . 4
1. Теориялық бөлім . . . 5
1. 1 Автоматты басқару жүйесінің математикалық моделін құру . . . 5
1. 2 Күйлер кеңістігіндегі математикалық модельдердің берілу түрлері . . . 5
1. 3 Көпөлшемді, көпбайланысты жүйелердің математикалық моделі . . . 9
1. 4 Модальды басқару әдісімен реттегішті жобалау . . . 10
1. 5 Тиімді дискретті бақылаушы құрылғыны құру . . . 12
1. 6 Көп байланысты көпөлшемді басқару жүйесі үшін агрегативті
салыстыру жүйесін құрастыру . . . 14
2. Есептік бөлім
2. 1 Ішкі жүйелердің сипаттамалық полиномдарын алу, көпөлшемді
басқару жүйесінің беріліс функциясын алу . . . 17
2. 2 Ішкі жүйелер математикалық модельдерінің қалыпты формасы . . . 17
2. 3 Ішкі жүйелер математикалық модельдерінің канондық формасы . . . 18
2. 4 Көпөлшемді басқару жүйесінің беріліс функциясы . . . 20
2. 5 Модальды басқару әдісімен реттегішті жобалау . . . 21
2. 6 Тиімді дискреттеу бақылаушы құрылғыны құру . . . 22
2. 7 Көпбайланысты көпөлшемді басқару жүйесі үшін
агрегативті салыстыру жүйесін құрастыру . . . 24
Қорытынды . . . 30
Қолданылған әдебиет . . . 31
Қосымша A . . . 32
Қосымша Ә . . . 33
Қосымша Б . . . 34
Қосымша В . . . 35
Қосымша Г . . . 36
Қосымша Д . . . 37
Курстық жобаға берілетін бастапқы мәліметтер
Вариант № 1, 3
1) Дифференциалдық теңдеулер жүйесі түрінде берілген көпөлшемді көпбайланысты басқару жүйесінің математикалық моделі:
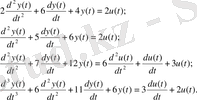
2) Көпөлшемді көпбайланысты басқару жүйесінің 4 ішкі жүйеден
тұратын құрылымдық сұлбасы (1-сурет) берілген.
Сурет 1 - Көпөлшемді және көпбайланысты басқару жүйесінің сұлбасы
3) Модальды басқару әдісімен реттегішті құру кезінде қажетті динамиканы η=10 орнықтылық дәрежесін қамтамасыз ететіндей алу керек.
Дискреттеу периоды T=0, 1.
4) Тиімді дискретті бақылаушы құрылғыны синтездеу үшін берілетін мәліметтер:
, ε =0, 01, u 0 =u n =-1,
,
, T=0, 1.
- Hматрицасының параметрлері:
h 1 =2, h 2 =4, h 3 =7.
Кіріспе
Қазіргі кезде әр түрлі жүйелер мен процесстерді жобалауда синтездеу есептері (жобалауда синтездеу деп берілген сапа көрсеткіштері мен жұмыс істеу шарттарына сәйкес жүйе немесе процесстің параметрлерінің құрылымын анықтауды білдіреді) ең маңызды, сонымен қатар ең күрделі болып табылады. АБЖ-дегі синтездеудің дәстүрлі әдістерін жүзеге асырғанда оларға келесі талаптар қойылады: ЭЕМ-дағы есептеулердің жылдамдығы және тұрақтылығы, ЖАЖ АБЖ жалпы идеологиясына сәйкес әдістердің пайдалануының әдістемелік ыңғайлығы, синтездеу критерийлерінің АБЖ құрастырушылары пайдаланатын критерийлеріне жеткілікті түрде жақындығы немесе ең болмағанда қарсы мағыналы болмауы.
1. ТЕОРИЯЛЫҚ БӨЛІМ
1. 1 Автоматты басқару жүйесінің математикалық моделін құру
Басқару объектінің математикалық моделі келесі дифференциалдық теңдеумен сипатталатын болсын:
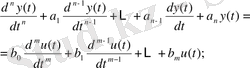 (1)
(1)
мұндағы u(t) - басқару әсері және y(t) - шығыс сигналы.
(1) теңдеуі дербес жағдайда төменгідей болады:
(2)
(2) теңдеуін шешу үшін оны Лаплас түрлендіруін қолдана отырып, операторлық түрге келтіреді:
(3)
(3) теңдеуінен шығады:
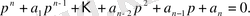 (4)
(4)
(4) теңдеуі сипаттамалық полином (көпмүшелік теңдеу) деп аталады. Осы (4) сипаттамалық полиномының
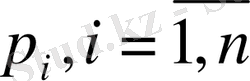 түбірлері болады. Бұл түбірлерге сәйкес (2) біртекті дифференциалдық теңдеудің шешімі келесі түрде болады:
түбірлері болады. Бұл түбірлерге сәйкес (2) біртекті дифференциалдық теңдеудің шешімі келесі түрде болады:
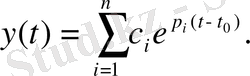 (5)
(5)
(5) шешімінің негізінде және де
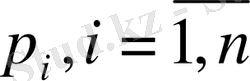 түбірлерінің негізіндегі (1) объектісінің орнықтылық сияқты динамикалық қасиеттерін зерттеуге болады, сонымен қатар модальды басқару әдісімен реттегішті синтездеу есебі шешіледі.
түбірлерінің негізіндегі (1) объектісінің орнықтылық сияқты динамикалық қасиеттерін зерттеуге болады, сонымен қатар модальды басқару әдісімен реттегішті синтездеу есебі шешіледі.
1. 2 Күйлер кеңістігіндегі математикалық модельдердің берілу түрлері
Қазіргі кезде (1) жүйесінің динамикалық қасиеттерін анализдеу және оны синтездеу есебін шешу үшін математикалық моделін күйлер кеңістігінде сипаттау қолданылады, оған өту үшін қалыпты (қарапайым) формасы, канонды формасы және т. б. қолданылады.
Қалыпты формасы
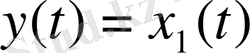 түрлендіруі негізінде алынады. Бұл түрлендіруге сәйкес (1) теңдеуінің басқа элементтері келесі түрде болады:
түрлендіруі негізінде алынады. Бұл түрлендіруге сәйкес (1) теңдеуінің басқа элементтері келесі түрде болады:
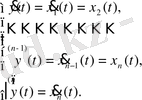 (6)
(6)
(6) жүйесінің соңғы теңдеуін
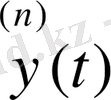 функциясына қатысты шешіп, (6) теңдеулерін
функциясына қатысты шешіп, (6) теңдеулерін
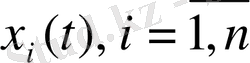 айнымалылары арқылы жазудың нәтижесінде келесі жүйені алуға болады:
айнымалылары арқылы жазудың нәтижесінде келесі жүйені алуға болады:
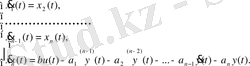 (7)
(7)
Дифференциалдық теңдеулер жүйесі (7) күйлер кеңістігіндегі математикалық модель болып табылады. Жүйенің матрицалық түрін күйлер айнымалыларының векторын енгізу арқылы алуға болады:
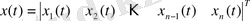
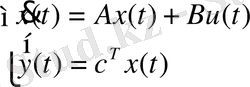
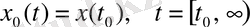 (8)
(8)
 (9)
(9)
мұндағы t - үздіксіз уақыт;
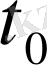 - бастапқы уақыт;
- бастапқы уақыт;
 - басқару объектісінің күйлер векторы;
- басқару объектісінің күйлер векторы;
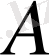 - элементтері
- элементтері
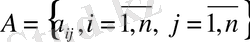 болатын, өлшемі
болатын, өлшемі
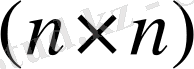 матрица (Фрабениус матрицасы) ;
матрица (Фрабениус матрицасы) ;
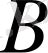 - элементтері
- элементтері
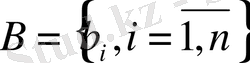 болатын, өлшемі
болатын, өлшемі
 вектор-бағана;
вектор-бағана;
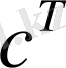 - бақылану векторы.
- бақылану векторы.
Қалыпты форманың екінші түрі:
Бұл түрін (1) теңдеуіндегі басқару туынды белгісінің астында болған жағдайда қолданады. Екінші қалыпты форма беріліс функциясына қатысты теңдеу негізінде құрылады:
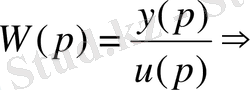
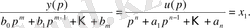 (10)
(10)
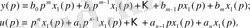 (11)
(11)
Басқару әсерін және шығыс сигналын уақыт бойынша функцияға түрлендіру қажет:
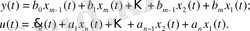 (12)
(12)
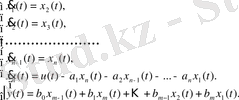 (13)
(13)
(13) теңдеулер жүйесінің матрицалық түрі:
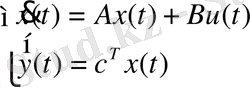
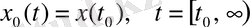
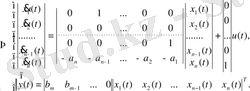 (14)
(14)
Қалыпты форманың үшінші түрі:
(1) дифференциалды теңдеуінде m және n дәрежелері бір-біріне тең болған кезде қалыпты форманың үшінші түрін қолданған дұрыс.
Күйлер кеңістігіндегі матрицалық түрі келесідей болады:
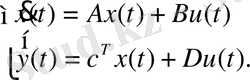
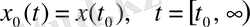
 (15)
(15)
B
матрицасының
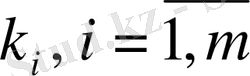 элементтері келесі жолмен табылады:
элементтері келесі жолмен табылады:
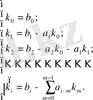 (16)
(16)
Күй кеңістігіндегі математикалық модельдің канондық формасы:
Бұл форма негізінде бастапқы беріліс функциясын қосылғыштарға жіктеу әдісі жатыр.
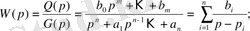 (17)
(17)
B матрицасының элементтері:
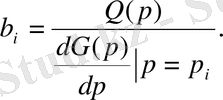 (18)
(18)
мұндағы
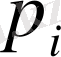 -
-
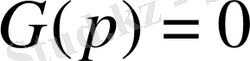 теңдеуінің түбірлері.
теңдеуінің түбірлері.
Дифференциалдық теңдеулер жүйесі түріндегі математикалық моделі:
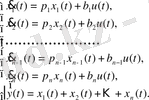 (19)
(19)
Матрицалық түрі:
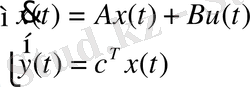
 (20)
(20)
мұндағы
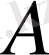 - элементтері
- элементтері
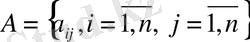 болатын, өлшемі
болатын, өлшемі
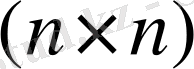 диагональды күйлер матрицасы (Жорданов матрицасы) .
диагональды күйлер матрицасы (Жорданов матрицасы) .
Екінші канондық формасы (Лурье формасы)
Бұл форма негізінде де қосылғыштарға жіктеу әдісі жатыр.
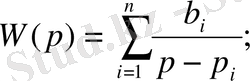
Түрлендіру формасы:
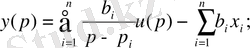
Сонда күй кеңістігіндегі математикалық модель мына түрде болады:
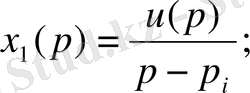
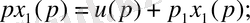
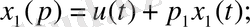
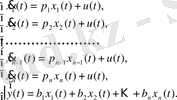 (21)
(21)
Жүйенің матрицалық түрі:
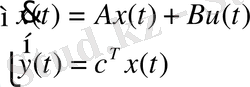
 (22)
(22)
1. 3 Көпөлшемді, көпбайланысты жүйелердің математикалық моделі
Көпөлшемді деп бірнеше кірісі мен бірнеше шығысы бар жүйелерді айтамыз. Мұндай жүйелердің әрбір кірісі мен шығысы n -дәрежелі дифференциалдық теңдеумен сипатталуы мүмкін. Ал осындай жүйенің көп байланыстылығы көпөлшемді жүйенің кірістері мен шығыстарының арасындағы байланыстармен сипатталады.
Айталық екі өлшемді басқару объекті берілсін:
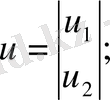
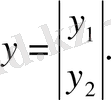
u кіріс сигналы вектор-баған түрінде беріледі. Ол y шығыс сигналымен беріліс функция бойынша байланысады. Жүйенің беріліс функциясы:
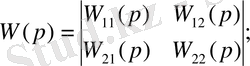 (23)
(23)
Екінші канондық формасының заңы бойынша, (23) беріліс функциясын келесі түрде жазуға болады:
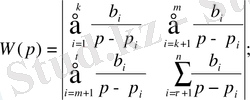
мұндағы k, m, τ, n - ішкі жүйенің өлшемі.
Күйлер кеңістігіне өту үшін y-ке қатысты өрнек алу керек:
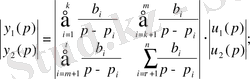
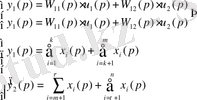
Көп өлшемді жүйенің күй кеңістігіндегі математикалық моделі:
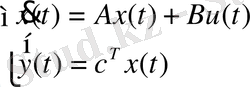
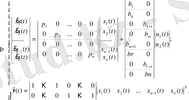 (24)
(24)
1. 4 Модальды басқару әдісімен реттегішті жобалау
Берілген әдістің ерекшелігі - әдетте реттегіш „жадысыз“ жүйе ретінде синтезделуі болып табылады. Яғни реттегіштің шығысы немесе u(t) басқару сигналы t уақыт моментінде x(t) күйлер векторының функциясы, немесе сол t уақыт моментіндегі
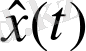 оның бағалауы болып табылады. Бұл жағдайда k матрицасының динамикалық (яғни инерциялық, интегралдаушы, дифференциалдаушы) үзбелері болмайды, алайда ол уақытқа тәуелді болуы мүмкін.
оның бағалауы болып табылады. Бұл жағдайда k матрицасының динамикалық (яғни инерциялық, интегралдаушы, дифференциалдаушы) үзбелері болмайды, алайда ол уақытқа тәуелді болуы мүмкін.
Айталық, басқару объектісінің математикалық моделі дифференциалды теңдеулер жүйесі түрінде берілсін:
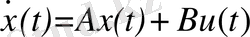 x(0) =x0, t∈[t0, tk], (25)
x(0) =x0, t∈[t0, tk], (25)
мұндағы t - үзіліссіз уақыт,
t 0 - бастапқы уақыт,
A - A={aij, i, j=[1, n] } элементті бар ( nxn ) матрица,
В - B={bi, i=[1, n] } элементті бар ( nx1 ) өлшемді вектор-баған.
u=-kx(t) түрдегі реттеу заңын құру, мұндағы к = к1, к2, . . . тұйықталған жүйеде процестің алдын-ала берілген динамикасын қамтамасыз етеді, демек
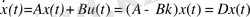 .
.
k баптау параметрлер векторын қажетті түрде таңдай отырып сипаттамалық полиномның керекті мәндерін алуға болады:
det(pE - A) = 0,
бұлар (1) жүйенің шешімінің өрнегінде, x(0) =x0 бастапқы шарттары берілген, құрауыштарына (модаларына) тиісті болады:
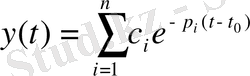
Реттеу заңын былай анықтау модальды басқару әдісі деп аталады. Тұйықталған теңдеулер жүйесінің керекті динамикасы мына түрде беріледі:
(nxn) өлшемді D матрицасы;
тұйықталған жүйесінің сипаттамалық полиномы:
det (pE-D) =pn+c1pn-1+ . . . +cn;
Тұйықталған жүйенің сипаттамалық полиномының түбірлері p1, p2;
Қажетті η орнықталық дәрежесіне сәйкес болатын тұйықталған жүйенің сипаттамалық полиномының түбірлері: p1=-η, p2=-η, …, pn=-η.
Басқару контурында цифрлі ЭЕМ-ді реттегіш ретінде пайдаланғанда үздіксіз жүйенің бөлікті-тұрақты кіріске реакциясын ескеру қажеттілігі туады, оның кірісіне үздіксіз объектінің күй векторы беріледі, ал оның шығысынан объектінің басқарушы кірісті әсер етулері алынады.
Бұл жағдайда, моделі ЭЕМ-де сақталатын реттегіш синтезі кезінде бөлікті-тұрақты кірісті автоматты реттеудің үздіксіз жүйесінің дискреттік моделіне
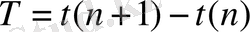 =const>0 - дискреттеу периоды, n = 0, 1, 2, . . . - дискреттік уақыт арқылы өтеді.
=const>0 - дискреттеу периоды, n = 0, 1, 2, . . . - дискреттік уақыт арқылы өтеді.
Айталық, дискретті басқару объектісінің математикалық моделі дискретті-айырымдық теңдеулер жүйесімен берілсін:
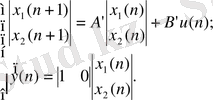 (26)
(26)
мұндағы A’=E + AT, B’= BT (А және В деп (1) теңдеудегі А мен В-ны түсінеміз) .
Тұйықталған жүйеде пропорционалды басқару заңының көмегімен алдын-ала берілген процесс динамикасын қамтамасыз ету қажет:
u(n) = -kx(n), k =k1, k2, . . .
Бұл мына алгоритм көмегімен жүзеге асады:
қадам 1. H 1 матрицасын құру:
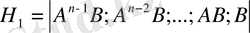 . (27)
. (27)
Қадам 2. Басқару жүйесінің тұйықталмаған және тұйықталған сипаттамалық коэффициенттерін алу. Басқару объектісінің матрицасы бойынша құрамыз:
det(pE - A’) = pn + a1pn-1 + . . . + an-1pn-2 + an,
det(pE - D) = pn+ c1pn-1 + . . . + cn.
қадам 3. H 2 матрицасын құру:
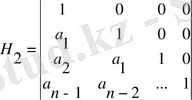 (28)
(28)
қадам 4. Екі матрицаны көбейтеміз:
 (29)
(29)
қадам 5. d көмекші векторын құрамыз:
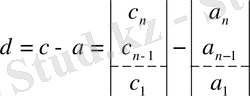 (30)
(30)
қадам 6. Q -1 кері матрицасын анықтау.
Қадам 7. баптау параметрлерінің векторын анықтау:
К = Q -1 d. (31)
қадам 8. Есепті шешудің дұрыстығын тексеру:
det(pE - D) = det (pE - A’ + B’kT) . (32)
қадам 9. Дұрыс шешімді таңдау: басқару алгоритмінің құрылымы және табылған k баптау параметрлерінің векторы беріледі:

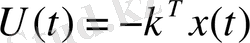 . (33)
. (33)
1. 5 Тиімді дискретті бақылаушы құрылғыны құру
Бақылаушы құрылғы деп инерциясыз кері байланыспен тұйықталған объектінің моделі бар динамикалық жүйені айтамыз.
Айталық басқару объектісінің дискретті математикалық моделі дискретті теңдеулер жүйесі түрінде берілсін:
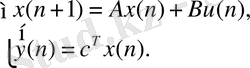 (34)
(34)
Шығыс сигналы y(n) бойынша өлшеуге болатын x(n) күйлер векторының барлық элементтерін қайта қалпына келтіруге мүмкіндік беретін дискретті бақылаушы құрылғының математикалық моделі келесі түрде болады:
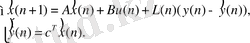 (35)
(35)
Бақылаушы құрылғыны құрудың есебі Ln, n=0, 1, 2, . . . тізбегін бақылаушы құрылғының қозғалысының траекторияларында таңдап алынған сапа критериі минималданытындай етіп таңдауға келтіреді.
Күй векторларын қалпына келтіру қатесін еңгізейік:
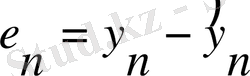
Квадраттық сапа критерийін мына түрде таңдайық:
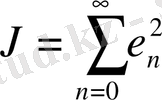 .
.
Тиімді дискретті бақылаушы құрылғыны құру есебінің қойылымы. Егер (34) басқару объектісінің математикалық моделі бақыланғыштық қасиетіне ие болса, онда бақылаушы құрылғыны синтездеуге болады, яғни бақылаушы құрылғының баптау параметрлерінің тізбегін қозғалыс траекториясында квадраттық сапа критерийі минималданатындай етіп таңдау қажет:
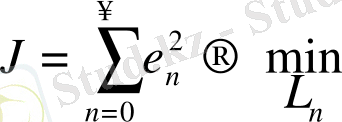 (36) Тиімді дискретті бақылаушы құрылғыны құрудың алгоритмі келесі қадамдардан тұрады:
(36) Тиімді дискретті бақылаушы құрылғыны құрудың алгоритмі келесі қадамдардан тұрады:
Қадам 1. n=0.
Қадам 2. Басқарылатын объектінің қозғалысын модельдейміз.
x(n+1) =Ax(n) + Bu(n),
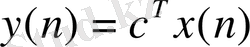 ,
,
Қадам 3. Бақылаушы құрылғының баптау параметрлерінің векторының мәнін анықтаймыз:
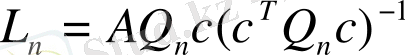 (37)
(37)
Қадам 4. Тиімді дискретті бақылаушы құрылғының қозғалысын модельдейміз.
(38)
Қадам 5. Таңдап алынған квадраттық сапа критерийінің n+1 қадамдағы мәнін анықтаймыз.
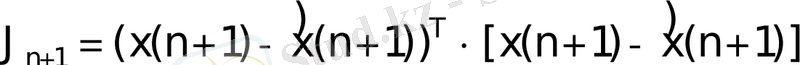 (39)
(39)
Қадам 6. Алынған сапа критерийінің мәнін қателер векторының қалпына келген құрауыштарының берілген дәлдігімен тексереміз. Егер бұл теңсіздік орындалса, онда қадам 9 өтеміз, ал орындалмаса, келесі 7 қадамға өтеміз.
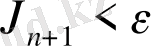
Қадам 7. Қалпына келтіру қателері матрицасының келесі мәндерін аламыз:
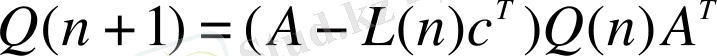 . (40)
. (40)
Қадам 8. Дискретті уақытты көбейтеміз: n=n+1 және келесі итерацияны орындаймыз, яғни 2 қадам өтеміз.
Қадам 9. Жобалық шешімді шығару: бақылаушы құрылғының математикалық моделінің құрылымы:

және Ln реттелетін параметрлер векторының мәні.
1. 6 Көп байланысты көпөлшемді басқару жүйесі үшін агрегативті салыстыру жүйесін құрастыру
Айталық, көпбайланысты басқару жүйесінің математикалық моделінің өзара әртүрлі кіріс-шығысты әр түрлі байланыстармен байланысқан k санды ішкіжүйелерден тұратын болсын.
Әр k-шы ішкіжүйе келесідей математикалық модельмен сипатталсын:
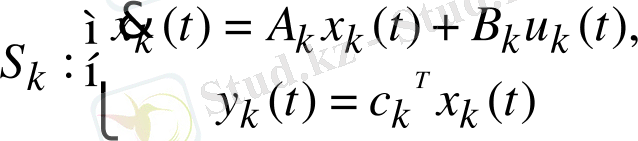
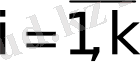 (41)
(41)
мұндағы t- үзіліссіз уақыт,
t0 - бастапқы уақыт,
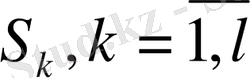 - ішкіжүйенің математикалық моделі
- ішкіжүйенің математикалық моделі
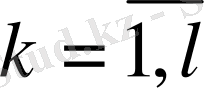 ,
,
l - ішкіжүйелер саны,
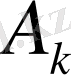 -
-
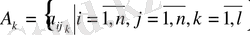 элементті
элементті

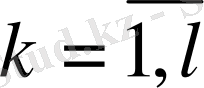 , өлшемді ішкіжүйенің күйлерінің матрицасы,
, өлшемді ішкіжүйенің күйлерінің матрицасы,
 ,
,
 , …
, …
 , - ішкіжүйенің айнымалы күйлерінің векторы
, - ішкіжүйенің айнымалы күйлерінің векторы
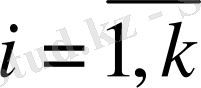 ,
,
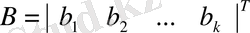 ,
,
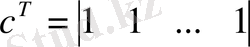 - сәйкес диагональды емес матрицаның өлшеміне матрицаның өлшемі тікелей тәуелді,
- сәйкес диагональды емес матрицаның өлшеміне матрицаның өлшемі тікелей тәуелді,
мұндағы
x(t) ∈Rn - басқару объектісінің күйлерінің векторы,
 - басқару,
- басқару,
A - A={aij, i, j=[1, n] } элементті (nxn) матрица,
В - B={bi, i=[1, n] } элементті (nx1) өлшемді вектор-баған.
1-қадам. Ішкіжүйелер арасындағы байланысты ескере отырып, көпөлшемді салыстыру жүйесінің математикалық моделін құру.
Ішкіжүйелер кірісі мен шығысы арасындағы байланысты орнату:
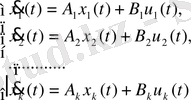
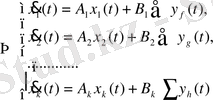
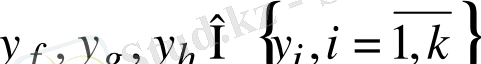
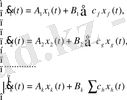
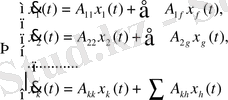 (42)
(42)
А 11
(p×p)
A 12
(p×r)
A 1k
(p×t)
A 21
(r×p)
А 22
(r×r)
A 2k
(r×t)
A k1
(t×p)
A k2
(t×r)
А kk
(t×t)
Мұндағы,
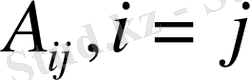 - диагональды матрицалары ішкіжүйелердің ішкі динамикасын бейнелейді.
- диагональды матрицалары ішкіжүйелердің ішкі динамикасын бейнелейді.
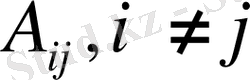 - диагональды емес ішкіжүйелердің өзара байланысын бейнелейді (егер кез келген
- диагональды емес ішкіжүйелердің өзара байланысын бейнелейді (егер кез келген
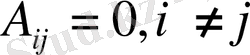 , онда бұл ішкіжүйелер байланыспаған) .
, онда бұл ішкіжүйелер байланыспаған) .
2-Қадам. Таңдап алынған Ляпунов функциясы, алынған Ляпунов функциясы туындысы және Ляпунов функциясы градиентінің нормасына бағалау коэффициенттерін алу.
Әр ішкіжүйе үшін Ляпунов функциясының өрнегін алу:
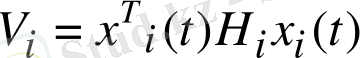
мұндағы H - симметриялы оң анықталған матрица.
Ляпунов функциясының туындысының және Ляпунов функциясының градиент нормасының өрнегін алу:
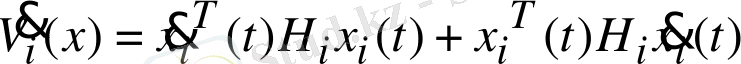 , (43)
, (43)
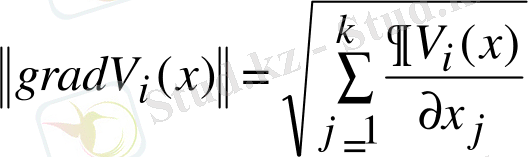 . (44)
. (44)
Бағалау коэффициенттерін алу және теңсіздіктерді тексеру:
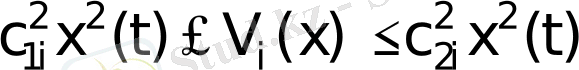 , (45)
, (45)
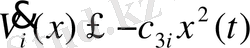 , (46)
, (46)
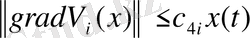 , (47)
, (47)
мұндағы
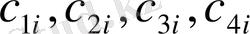 - бағалау коэффициенттері:
- бағалау коэффициенттері:
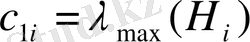
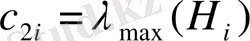
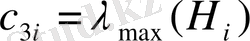 ,
,
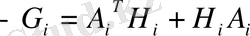 , (48)
, (48)
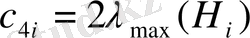
3-қадам. Салыстыру теңдеуін құру.
Қадам 2 алынған бағалау коэффициенттерінің негізінде
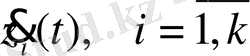 айнымалыларына байланысты агрегативті салыстыру жүйесін құру, оның математикалық моделі
айнымалыларына байланысты агрегативті салыстыру жүйесін құру, оның математикалық моделі
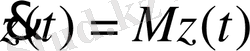 түрде болады,
түрде болады,
Мұндағы М тұрақтылар матрицасы
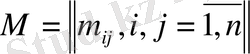 түрде болады,
түрде болады,
мұндағы
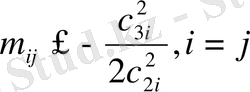 (49)
(49)
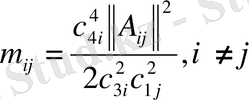 . (50)
. (50)
Салыстыру теңдеуінің өрнегі мына түрде болады:
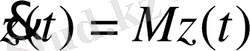 (51)
(51)
қадам 4. Салыстыру теңдеуі негізінде көпбайланысты күрделі жүйенің тұрақтылық қасиетін зерттеу. (52)
Берілген қадам келесі критерий негізінде жүзеге асады.
 өлшемді Ì-матрицаны оның барлық жүп тізбекті бас минорлары оң, ал тақ минорлары теріс болған жағдайда ғана тұрақты болады:
өлшемді Ì-матрицаны оның барлық жүп тізбекті бас минорлары оң, ал тақ минорлары теріс болған жағдайда ғана тұрақты болады:

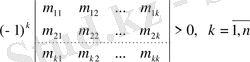 .
.
2. ЕСЕПТІК БӨЛІМ
2. 1 Ішкі жүйелердің сипаттамалық полиномдарын алу, көпөлшемді
басқару жүйесінің беріліс функциясын алу
Ішкі жүйелердің дифференциалдық теңдеулеріне сәйкес алынған операторлық түрін алу:
1-ші ішкі жүйе:
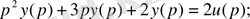
2-ші ішкі жүйе:
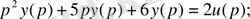
3-ші ішкі жүйе:
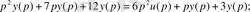
4-ші ішкі жүйе:
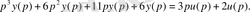
Сипаттамалық полиномдар:
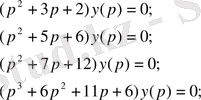
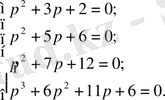
2. 2 Ішкі жүйелер математикалық модельдерінің қалыпты формасы
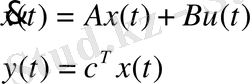
1-ші ішкі жүйе:
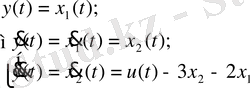
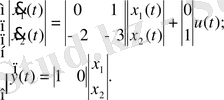
2-ші ішкі жүйе:
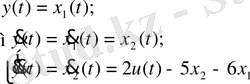
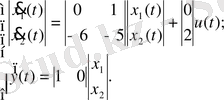
3-ші ішкі жүйе үшін 3-ші қалыпты түрдегі математикалық модель:

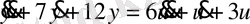
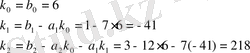
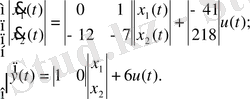
4-ші ішкі жүйе үшін 2-ші қалыпты түрдегі математикалық модель:
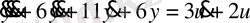
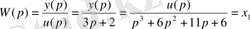
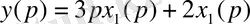
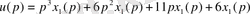
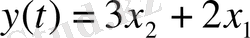
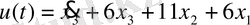
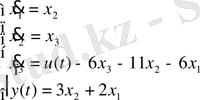
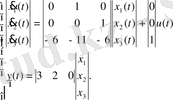
2. 3 Ішкі жүйелер математикалық модельдерінің канондық формасы:
1-ші ішкі жүйе:
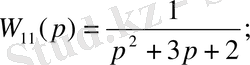
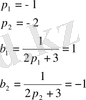
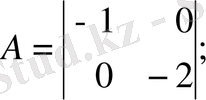
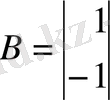
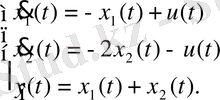
2-ші ішкі жүйе:
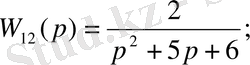
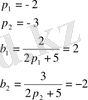
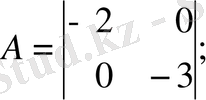
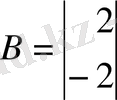
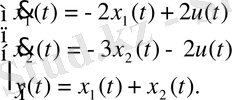
3-ші ішкі жүйе:
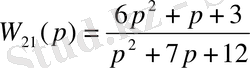
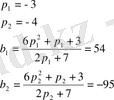
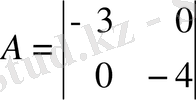
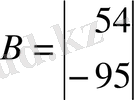
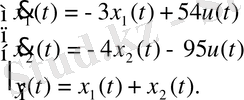
4-ші ішкі жүйе:
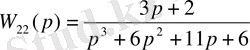


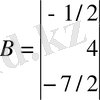
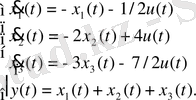
Автоматты басқару жүйесін ішкіжүйелерін орнықтылыққа тексеру
Автоматты басқару жүйесінің ішкіжүйелерін Михайлов критерийі бойынша орнықтылыққа тексереміз.
1-ішкіжүйе:
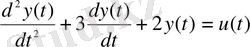
Бұл ішкіжүйенің беріліс функциясы
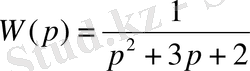
Осы теңдеудің сәйкес түрі болып, мына теңдеуді жазуға болады:
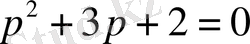
Осы теңдеудегі р-ны jw-ға алмастыра отырып, сипаттаушы теңдеудің жаңа түрін алуға болады:
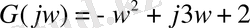
Бұл теңдеу комплексті болғандықтан, оны нақты және жорамал бөлікке бөлуге болады.
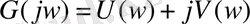
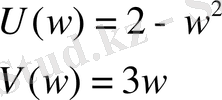
w-ны нөлден шексіздікке өзгерте отыра, U-V комплекстік жазықтығында нақты осінен басталатын Михайлов годографы сызылады.
Кесте 1
Осы ішкіжүйенің Михайлов годографы қосымша Ә-де келтірілген.
2-ішкіжүйе:
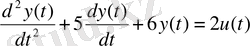
Оның беріліс функциясы
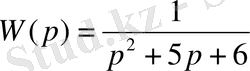
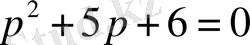
Осы теңдеудегі р-ны jw-ға алмастыра отырып, сипаттаушы теңдеудің жаңа түрін алуға болады:
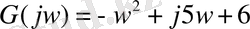
Нақты және жорамал бөлікке бөлеміз
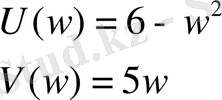
Кесте 2
Осы ішкіжүйенің Михайлов годографы: қосымша Ә-де келтірілген.
3-ішкіжүйе:
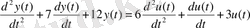
Беріліс функциясы
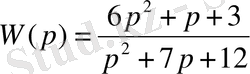
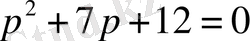
Осы теңдеудегі р-ны jw-ға алмастырамыз
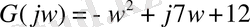
Нақты және жорамал бөліктерін ажыратамыз
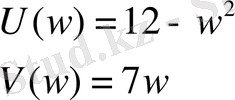
Кесте 3
Осы ішкіжүйенің Михайлов годографы қосымша Ә -де келтірілген.
4-ішкіжүйе:
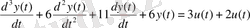
Беріліс функциясы
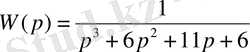
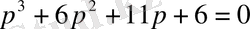
Осы теңдеудегі р-ны jw-ға алмастыра
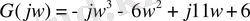
Нақты және жорамал құраушыларына бөлеміз
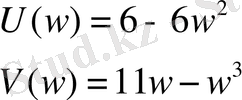 :
:
Кесте 4
Осы ішкіжүйенің Михайлов годографы қосымша Ә-де келтірілген.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz