Delphi ортасындағы графиканың мүмкіндіктері

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 19 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ . . . 3

1 БӨЛІМ. DELPHI ОРТАСЫНДАҒЫ ГРАФИКАНЫҢ

МҮМКІНДІКТЕРІ

1. 1 Функция ұғымы және оның берілуі . . . 4

1. 2 Delphi ортасында график салудың мүмкіндіктері . . . 8

1. 3 Графикалық құралдарды қолдану . . . 12

2 БӨЛІМ . DELPHI ОРТАСЫНДАҒЫ ГРАФИКАНЫҢ ТҰРҒЫЗУ

2. 1 Мултьимедиалық жүйелердің функциялар графигі . . . 14

2. 2 Функцияның графиктері . . . 15

2. 3 Бір айнымалы функция графигін құру . . . 19

ҚОРЫТЫНДЫ . . . 22

Қоданылған әдебиеттер тізімі . . . 23

Қосымша. . . . 24

КІРІСПЕ

Функцияның графиктерін салу-кез келген білім алушының ойлау қабілетін арттырады, білім дәрежесін барынша жетілдіреді, зерттеудің графикалық әдісін меңгеруіне үйретеді Сол себепті менің курстық жұмысымның негізгі мақсаты болып зерттелетін функциялардың электронды түрде, сонымен қатар Delphi бағдарламасының көмегімен графигін тұрғызу болып табылады. Кез келген оқытушы математика пәнінен функция графигі жөнінде тақырып өткізетін болса, онда сол тақырып бойынша тақтаға сызып графигін тұрғызбай-ақ электронды түрде осы бағдарламаны көрсете алады.

Математикадан сынақтарда көптеген есептерді шешу барысында графикті салу есептің шешуін едәуір қысқартады немесе оны шешу әдісін табуға көмектеседі.

Курстық жұмыстың мақсаты: графикалық объектілермен жұмыс жасай отырып, бағдарламада анықталған функция бойынша графигін тұрғызу болып табылады.

Курстық жұмыстың негізгі міндеттері:

функцияны зерттеу;
зерттелінген функция бойынша графигін тұрғыза білу;
график тұрғызу үшін бағдарламалау ортасын зерттеу.

1 БӨЛІМ. DELPHI ОРТАСЫНДАҒЫ ГРАФИКАНЫҢ

МҮМКІНДІКТЕРІ

Функция ұғымы және оның берілуі

Функция (лат. functіo - орындау, атқару, жүзеге асыру) математикадағы ұғым

Қызмет, міндет, жұмыс; қатынастар жүйесіндегі қайсы бір объекті қасиеттерінің сыртқы көрінісі;
Социологияда - белгілі бір әлеуметтік институт атқаратын рөл;
Лингвистикада - тілдік бірліктің немесе тіл құрылымы.

Егер мүмкін мәндер жиынтығынан алынған х-тің әрбір мәніне айнымалы у-тің белгілі бір мәні сәйкес келсе, онда у айнымалы шамасы х айнымалы шамасының функциясы деп аталады. Мұндай тәуелділік у=f(х) түрінде жазылады. f әрпінің орнына басқа әріптер де, т. б. ) қолданылады. Мұндағы х-ті тәуелсіз айнымалы (кейдеψ, ϕ(мыс., F, аргумент) деп, ал оның өзгеру облысы (жиыны) у-тің анықталу облысы деп аталады. х-тің өзгеруіне байланысты айнымалы у-тің қабылдайтын мәндерінің жиынын у функциясының өзгеру облысы деп атайды. Функцияның жоғарыда берілген анықтамасында назар аударатын екі жағдай бар: біріншісі - аргумент х-тің өзгеру облысын көрсету, екіншісі - х пен у мәндерінің арасындағы сәйкестік ережені немесе заңды тағайындау. Егер х-тің бір мәніне у-тің бір ғана мәні сәйкес келсе, онда у-ті х-тің бір мәнді Функциясы деп, ал егер х-тің бір мәніне у-тің бірнеше мәні сәйкес келсе, онда у-ті х-тің көп мәнді функциясы деп атайды [1, 7-15] .

Айнымалы шамалар (х пен у) мәндерінің арасындағы сәйкестік ережені немесе заңды функц. тәуелділік дейді. Функция көбінесе аналитикалық тәсіл немесе формула арқылы (мысалы, , т. б. ), кейде графиктік және таблицалық (дәл не жуық формулалармен есептелген) тәсілдерімен де беріледі. Математиканың одан әрі дамуы нәтижесінде Функция табиғаты кез келген айнымалы математикалық объектілер арасындағы сәйкестік ретінде жалпыланды. Математиканың басқа ұғымдары тәрізді Функция ұғымы да бірден қалыптасқан жоқ. Ол дамудың ұзақ жолынан өтті. “Функция” термині алғаш рет 1692 ж. Г. Лейбництің еңбектерінде кездесті. Функцияның қазіргі ұғымға жақын алғашқы анықтамасын И. Бернулли (1718) берген, ал бұл ұғымды Д. Бернулли, Л. Эйлер, Ж. Фурье, П. Дирихле, Н. И. Лобачевский, т. б. одан әрі дамытты.

Дифференциалдық есептеудегі негізгі мақсаттың бірі функцияны зерттеу, яғни тәуелсіз айнымалының өзгеруіне байланысты тәуелді айнымалы қалай өзгеретінін зерттеу болып табылады (1-сурет) .

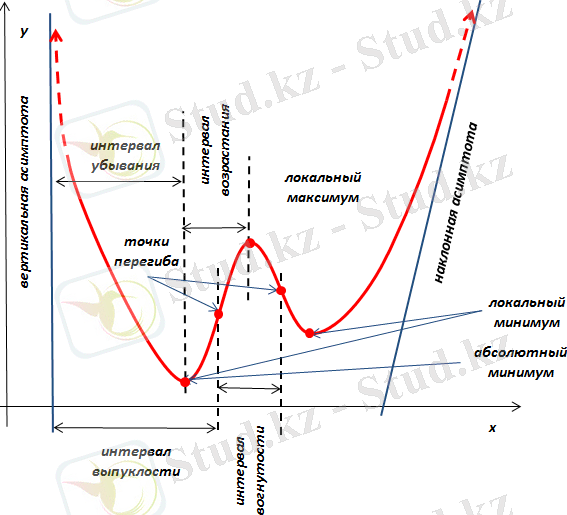
1-сурет. Тәуелсіз айнымалының өзгеруіне байланысты тәуелді айнымалы

Егер функция берілген аралықтағы аргументтің кез-келген екі мәні үшін аргументтің үлкен мәніне функцияның үлкен (кіші) мәні сәйкес келетін болса, онда функция осы аралықта өспелі (кемімелі) функция болады деп айтады. Яғни x ₁ <x ₂ болған кезде өспелі (кемімелі) функция үшін f(x ₁ ) <f(x ₂ ) (f(x ₁ ) >f(x ₂ ) ) болады. Ал егер x ₁ <x ₂ болған кезде f(x ₁ ) ≤f(x ₂ ) (f(x ₁ ) ≥f(x ₂ ) ) болатын болса, онда функция осы аралықта кемімейтін (өспейтін) функция болады деп айтамыз.

Енді функцияның өспелі (кемімелі) болуының белгілерін келтірелік.

1. Егер дифференциалданатын (туындысы бар) функциясы аралығында өспелі (кемімелі) болатын болса, онда осы аралықта оның туындысы оң (теріс) болады, яғни f'(х) >0 (f'(х) <0) .

2. Егер [а; b] аралығында дифференциалданатын (туындысы бар) функцияның туындысы осы аралықта оң (теріс) болатын болса, онда осы аралықта функция өспелі (кемімелі) болады [3, 25-27] .

Функция кемімейтін немесе өспейтін аралықтарды функцияның монотондық аралықтары деп айтады. Сонымен функция монтондық аралықтың бір түрінен екінші түріне көшкен кезде (мысалы өсу аралығынан кему аралығына) функцияның туындысы бар болатын болса, онда оның таңбасы өзгеруі керек екен. Функцияның туындысы нольге тең болатын, болмаса туындысы болмайтын нүктелерді критикалық нүктелер деп атайды.

Егер мейлінше аз болатын Δx≠0 үшін f(x ₁ +Δx) <f(x ₁ ) теңсіздігі орындалса, онда x ₁ нүктесі функцияның локальді максимум қабылдайтын (локальді максимум) нүктесі деп аталынады. Егер x ₂ нүктесі және мейлінше аз Δx≠0 үшін f(x ₂ +Δx) >f(х ₂ ) теңсіздігі орындалса, онда x ₂ нүктесі функциясының локальді минимум қабылдайтын (локальді минмум) нүктесі деп аталынады. Максимум мен минимумды біріктіріп экстремум деп атайды, ал функцияның максимумы мен минимумын функцияның экстремальдық мәндері деп атайды.

Теорема 1 (локальдік экстремум болуының қажетті шарты) . Егер y=f(х) функциясы х=х ₀ нүктесінде экстремум қабылдайтын болса, онда иә f'(х ₀ ) =0, иә f'(х ₀ ) болмайды.

Яғни локальдік экстремум қабылданатын нүктеде функцияның бірінші ретті туындысы нольге тең болады, немесе ол нүктеде функцияның туындысы болмайды (дифференциалданбайды) .

Экстремум қабылданатын нүктеде функцияның туындысы бар болатын болса, онда осы нүктедегі функция графигінің жанамасы абсцисса осіне параллель болады.

Теорема 2 (локальдік экстремум болуының бірінші жеткілікті шарты) . у=f(х) функциясы х=х ₀ критикалық нүкте жатқан бір аралықта үзіліссіз болып, осы аралықта туындысы бар болсын (критикалық нүктеде туындысы жоқ болуына болады) . Егер х<х ₀ болғанда f'(х) >0 болып, ал х>х ₀ болғанда f'(х) <0 болса, онда х=х ₀ нүктесінде функцияның максимумы бар; ал х<х ₀ болғанда f'(х) <0 болса, х>х ₀ болғанда f'(х) >0 болса, онда х=х ₀ нүктесінде функцияның минмумы бар [3, 29-30] .

Яғни туындысы бар функцияның туындысы критикалық нүктеден өткен кезде оның туындысы таңбасын плюстен минуске өзгертсе критикалық нүктеде максимум қабылдайды, ал туындының таңбасы керісінше өзгерсе онда критикалық нүктеде минимум қабылдайды екен.

Теорема 3 (функцияның локальдік экстремумы болуының екінші жеткілікті шарты) . у=f(х) функциясының х=х ₀ нүктесінде екінші ретті туындысы бар, және f'(х ₀ ) =0 болсын. Онда, егер f”(х ₀ ) <0 болса, х=х ₀ нүктесінде функция локальдік максимум қабылдайды, егер f”(х ₀ ) >0 болса осы нүктеде локальдік минимум қабылдайды.

Егер f”(х ₀ ) =0 болса х=х ₀ нүктесінде экстремум бар да, жоқ та болуы мүмкін.

Егер y=f(х) функциясының (а; b) аралығындағы графигі осы аралықтағы жанамаларының үстіне орналасса, онда функция осы аралықта ойыс болады дейді, ал егер осы аралықта өзінің жанамаларының астына орналасса дөңес болады дейді.

Егер М(х ₀ , f(х ₀ ) ) нүктесі функция графигінің дөңес және ойыс бөліктерін ажыратып тұрса, яғни М(х ₀ , f(х ₀ ) ) нүктесінің бір жағында дөңес, ал екінші жағында ойыс, немесе керісінше болса, онда М(х ₀ , f(х ₀ ) ) нүктесін функция графигінің иілу нүктесі деп атайды.

Теорема 4 (функция графигінің дөңес (ойыс) болуының жеткілікті шарты) . Егер (а; b) интервалының барлық нүктелерінде у=f(x) функциясының екінші ретті туындысы теріс (оң) болатын болса, яғни f”(х) <0 (f”(x) >0) болса, онда у=f(x) функциясының графигі осы аралықта дөңес (ойыс) болады.

Иілу нүктесінен өткен кезде функцияның екінші ретті туындысы өзінің таңбасын өзгертеті болғандықтан иілі нүктесінде екінші ретті туынды иә нольге тең болады, иә иілу нүктесінде функцияның екінші ретті туындысы болмайды [5, 27-29] .

1. 2 Delphi ортасында график салудың мүмкіндіктері

Delphi-де сурет салу - жеткілікті қарапайым үрдіс. Проектті жасап шығару кезінде сіздің ұйғарымыңызда мата (Canvas қасиеті), қарындаш (Реп қасиеті), қылқалам (Brush қасиеті) және қандай да бір көлемдегі қарапайым объектілер (сызықтар, төртбұрыштар, эллипстер, т. б. ) бар. Шынын айту керек, Canvas қасиеті барлық компоненттерде бар емес. Осы қасиетке ие компоненттер көбіне осылар: форма (TForm классы), кесте (StringGrid классы), растрлық сурет (TImage классы), принтер (TPrinter классы) . Қарындаш пен қылқаламның түсі (Color) мен стилін (Style) ауыстыруға болады. Осы құралдың жиыны математикалық және инженерлік мазмұнды жеткілікті деңгейде күрделі суреттерді салуға мүмкіншілік береді. Осыдан басқа Delphi Windows-тың көптеген қорларын пайдалануға мүмкіндік береді: графикалық файлдар, фильмдер және дыбыстық файлдар.

Мата - бұл, нүктелер (Pixels [X, Y] : Tcolor) деп аталатын кішкентай шаршылардан тұратын төртбұрышты тор. Әрбір нүктедің өз нөмірі, дәлірек айтқанда, екі нөмірі болады. Бірінші нөмір нүктенің көлденең орналасуын көрсе

тсе, екіншісі - тігінен орналасуын. Матаның сол жақ жоғарғы пикселінің координаты [0, 0] -Pixels[0, 0] . Көлденең бойынша барлық нүктелер саны Width қасиетімен анықталса, тігінен - Height қасиетімен. Әрбір нүкте Windows қолдайтын қандай да болмасын түспен боялуы мүмкін, және де матада нүктені салу Pixels жиымінің элементіне түстің нөмірі меншіктелген сәтте орындалады.

Мысалы, Image1. Canvas. Pixels[100, 100] := clRed нәтижесі - [100, 100] координаталы қызыл нүкте. Біз кез келген нүктедің түсінің нөмірін кері әрекет арқылы біле аламыз: Color:= Image1. Canvas. Pixels[100, 100] .

Нүктенің TColor түсінің классы ұзын бүтін болып анықталған, және де осындай типті айнымалылар жадыда төрт байт орын алады. Он алтылық жүйеде класс келесі диапазонға ие: TColor = - $8 . . S7. Осы типтің айнымалыларының төрт байты көк (В), жасыл (G) және қызыл (R) түстердің еншілері жайлы ақпаратты сақтайды да, келесідегідей қалыптасқан: S00BBGGRR. Әрбір түстің еншісі 0-ден 255-ке дейін өзгертілуі мүмкін. Сондықтан да қызыл нүктені салу үшін, біз оған SFF нөмірлі түсті меншіктеу керекпіз. Delphi-де түстерге арналған тұрақтылар жиынтығы бар. Осы түстердің тізімін объектіле инспекторында немесе Grahics модулінде көруге болады.

Дегенмен, матаның нүктелеріне екі өлшемді жиым Pixels[X, Y] арқылы қатынау - бұл сурет салудың ең баяу әдісі. Аса жылдам сурет салу үшін арнайы тәсілдерді пайдаланады: LiпеТо -сызықтар үшін; Arc -доға үшін; RectAngle - төртбұрыштар үшін; TextOut - мәтіді шығару үшін және т. б.

Image 1 компонентінің төсемінде Лиссажу қисықтарын салу.

Тапсырманы орындау технологиясы:

Жалпы түрде бұр қисықтар параметрлік теңдеулер көмегімен беріледі:

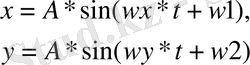
және де төрт параметрден тәуелді: wx, wy екі жиіліктен және w1, w2 фазалық ығысудан.

Біздің жұмыста осы функцияларды шығару үшін Fx және Fy әдістері қолданылады.

Лиссажу қисықтарын анықтайтын функциялар:

function TForm1. Fx(t:real) :real;

begin

Fx:=sin(wx*t+w1) ;

end;

function TForm1. Fy(t:real) :real;

begin

Fy:=sin(wy*t+w2) ;

end;

[8, 51-58] .

Жұмысты орындау кезінде wx, wy, w1 және w2 параметрлерін өзгерту үшін жалғыз формаға төрт TSpinEdit компонентін орнатамыз. Мәндердің анағұрлым бірқалыпты өзгеруін қамтамасыз ету үшін, TSpinEdit-тің негізгі қасиеті Value-ді 10-ға бөлейік. Мысалы, wx:=SpinEditWx. Value/10. Функцияның графигін қағазға салудың алдында, xI[x1, x2] және yI[y1, y2] айнымалыларының өзгеру интервалын бере отырып, сурет салу терезесін таңдаймыз. (x1, y1), (x2, y2) «қағаз» терезесінен (I1, J1), (I2, J2) экрандағы терезеге көшкенде, нүктенің координаттарын II(x) и JJ(y) функциясының көмегімен ауқымдау қажет:

Ауқымдау фунциялары:

Function TForm1. II(x:real) : integer;

{ОХ өсі бойынша ауқымдау функциясы}

Begin

II:=I1+Trunc((x-x1) *(I2-I1) /(x2-x1) ) ;

End;

Function TForm1. JJ(y:real) : integer;

{ОУ өсі бойынша ауқымдау функциясы}

Begin

JJ:=J2+Trunc((y-y1) *(J1-J2) /(y2-y1) ) ;

End;

Айнымалыларды инициализациялау:

Procedure TForm1. FormActivate(Sender:TObject) ;

Begin

n:=200;

x1:=-1. 2; x2:=1. 2; y1:=-1. 2; y2:=1. 2;

{экрандағы терезені орнату}

With Image1 do

Begin

I1:=0; J1:=0; I2:=width; J2:=height;

End;

{ОХ өсі бойынша қадамды есептеу}

h:=2*pi/n;

Drawgraphic;

End;

Графикті салу

Procedure TForm1. DrawGraphic;

Var i: integer;

t: real;

begin

wx:=SpinEditWx. Value/10;

wy:=SpinEditWy. Value/10;

w1:=SpinEditW1. Value/10;

w2:=SpinEditW2. Value/10;

with Image1. Canvas do

begin

Pen. Color:=clWhite;

Brush. Color:=clWhite;

RectAngle(0, 0, Width, Height) ;

{Координаттар өсін құру}

Pen. Color:=clBlack;

MoveTo(II(0), JJ(Y1) ) ; LineTo(II(0), JJ(Y2) ) ;

MoveTo(II(x1), JJ(0) ) ; LineTo(II(x2), JJ(0) ) ;

{Функцияның графигін бөлшектеп құру}

T:=0; x:=Fx(t) ; y:=Fy(t) ; MoveTo(II(x), JJ(y) ) ;

For i:=1 to 5*n do

Begin

T:=t+h; x:=Fx(t) ;

Y:=Fy(t) ; LineTo(II(x), JJ(y) ) ;

End;

SpinEditWx компоненті үшін SpinEditWx. Value қасиетін өзгерткен кезде графикті қайта салатын оқиғаны өңдеуішті тағайындаймыз:

SpinEditWx өзгергендегі оқиға

procedure TForm1. SpinEditWxChange(Sender:TObject) ;

begin

DrawGraphic;

End;

SpinEdit-тің басқа объектілері үшін объектілер инспекторында onChange оқиғасын SpinEditWxChange-ге бағыттаймыз.

1. 3 Графикалық құралдарды қолдану

Delphi ортасында құрылған қосымшалар сурет салу Canvas (кенеп, селдір мата, мата) қасиетіне ие компоненттерді қолдану арқасында ғана жүзеге асырылады. Әдетте, бұл қасиеттерге TForm, TStringGrid, TImage, TPrinter компоненттері ие. TCanvas және қалған барлық графикалық кластар үшін TPersistent класы арғы тегі болып табылады. TPersistent класының ұрпақтары:

Құралдар класын тудыратын TGraphicsObject класы;
Сурет салу әдістері мен құралдары бар TСanvas класы;
Файлдардың өз форматы бар бейнелердің төрт класын {TBitmap, TIcon, Tmetafile, TJPEGImage} тудыратын TGraphic класы;
TGraphic класының, дәлірек айтқанда оның ұрпақтарының қондырмасы болатын TPicture класы. Оның TGraphic өрісінде TBitmap, Ticon, TMetafile немесе TJPEGImage болуы мүмкін.

Графиканы бағдарламалау. Түсті, қылқалам қалыңдығын және құюды таңдау мүмкіндіктері бар графикалық редактор бағдарламасын жасап шығарыңдар.

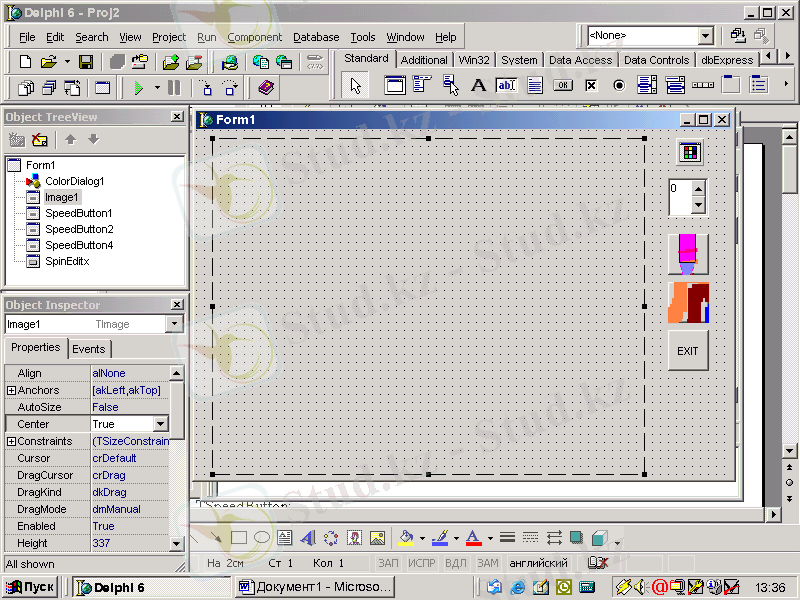
2-сурет.

Абстрактті TGraphic класы төрт түрлі кескіндер (иконка ( Ticori класы) , метафайл ( Tmetaflle класы) , растрлық кескін (класс Tbitmap ) и JPEG растрлық кескіні (класс TJPEGImage ) ) класының арғы тегі болып табылады. Осы төрт графикалық кластың TBitmap ішінен ғана TCanvas қасиетіне ие. TGraphic класының әдістері алдымен файлдармен, ағындармен және алмасу буферімен графикалық ақпаратпен алмасуға арналған.

Жаңа жұмыс ашып, формаға TSpeedButton батырмасын орнатыңыз. implementation кілтті сөзінен кейін модульде uses ShellAPI хабарламасын кірістіріп, форманың келесі OnShow оқиға өңдеуішін құрыңыз:

Тапсырманы орындау технологиясы:

implementation

uses ShellApi;

{$R *. DFM}

procedure TForm1. FormShow(Sender: TObject) ;

var

Icon: TIcon;

begin

Icon := TIcon. Create;

Icon. Handle:= ExtractIcon(0, 'C:\WINDOWS\NOTEPAD. EXE', 1) ;

SpeedButton. Glyph. Width:= Icon. Width;

SpeedButton1. Glyph. Height:= Icon. Height;

SpeedButton1. Glyph. Canvas. Draw(0, 0, Icon) ;

Icon. Free;

end;

2 БӨЛІМ . DELPHI ОРТАСЫНДАҒЫ ГРАФИКАНЫҢ ТҰРҒЫЗУ

2. 1 Мултьимедиалық жүйелердің функциялар графигі

Бірінші бөлімде параметрлі берілген функция графигін құру есебін қарастырылған. Енді нақтырақ талдау жасау үшін бір айнымалы функция графигін құрастыру есебіне оралсақ.

у = f(x) функция графигін қағазда салу үшін (X ₁ , X ₂ ) *(Y,, Y ₂ ) өлшемді тікбұрыш таңдалып алынады. Монитор экранында функция графигін салу кезінде туындайтын қиыншылық (X ₁ , X ₂ ) *(Y,, Y ₂ ) өлшемді тікбұрышты экрандағы тікбұрышқа масштабтауға тура келетінінде.

Бұрылған торда күңгірт түстердің көмегімен бейнелеу. Тордың параметрлік теңдеулерін сурет ретінде келтіретін боламыз:

x = (R + r0 * cosβ) * cosα;

y = (R + r0 * cosβ) * sinα;

z = r0 * sinβ.

R- координаттар басынан тордың өсіне дейінгі қашықтық, r0 - тордың радиусы, 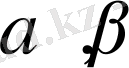- 0-ден 2 -ге дейін мән қабылдайтын бұрыштар.

II(x:real) : integer и JJ(y:real) : integer функциялары ауқымдауды жүзеге асырады, ал О1, О2 и О3 процедуралары - координаттар жүйесін Z, Y, X өстерін сәйкесінше айналуы. Мәндерді есептеуді жылдамдату үшін sinα және cosα 3 ⁰ қадамымен алдын ала есептеліп, co [0. . 120] және si [0. . 120] жиымдарына енгізіліп қойған.

Синустар және косинустар жиымін толтыру процедурасы

Procedure TForm1. FormCreate(sender:TObject) ;

Var i: integer;

Begin

for i:=0 to 120 do

begin

co[i] :=cos(Pi/60*i) ; si[i] :=sin(Pi/60*i) ;

end;

Тордың беткі қабаты тіктөртбұрыштарға бөлінген (9. 7 суреті) a=i*q, i=1. . n, b=j*h, j=1. . m.

Тіктөртбұрыштың түсі Z өсіне проекцияның ұзындығымен және төртбұрыштың бірлік нормалі 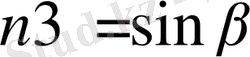анықталады, операторлармен жүзеге асырылады.

2. 2 Функцияның графиктері

unit U1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, StdCtrls.

type

TForm1 = class(TForm)

Button1: TButton;

procedure Button1Click(Sender:TObject) ;

procedure FormCreate(Sender:TObject) ;

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

imlementation

{$R *. dfm}

procedure TForm1. Button1Click(Sender:TObject) ;

var

x, y: real;

Px, Py, l, g:integer;

begin

l:=Form1. Height div 2;

begin

for Px:=0 to Form1. Width do begin

x:=Px*3*pi/Form1. Width;

y:=cos(x) ;

Py:=trunc(0. 5*y*1) +1;

Canvas. Pen. Width:=100;

for g:=1 to 1000 do Canvas. Pixels[Px, Py] :=clGreen;

end;

l:=Form1. Height div 2;

begin

for Px:=0 to Form1. Width do begin

x:=Px*3*pi/Form1. Width;

y:=cos(x) ;

Py:=trunc(0. 5*y*1) +1;

canvas. Pen. Width:=40;

canvas. Pixels[Px, Py] :=clRed;

for g:=1 to 1000 do

canvas. Pixels[Px, Py] :=clWhite;

canvas. Pixels[Px, Py] :=clRed;

for g:=1 to 1000 do

canvas. Pixels[Px, Py] :=clWhite;

canvas. Pixels[Px, Py] :=clYellow;

end;

procedure TForm1. FormCreate(Sender: TObject) ;

begin

Form1. Color:=clWhite;

end;

end.

Берілген функциялардың графиктерін салу: ; ;

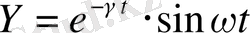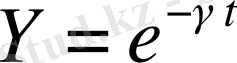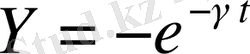
Тапсырманы орындау технологиясы:

unit Graph;

interface

uses

а Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,

StdCtrls, TeEngine, Series, ExtCtrls, TeeProcs, Chart;

type

TForm1 = class(TForm)

Edit1: TEdit;

Edit2: TEdit;

Edit3: TEdit;

Edit4: TEdit;

Edit5: TEdit;

Label2: TLabel;

Label3: TLabel;

Label4: TLabel;

Label5: TLabel;

Chart1: TChart;

Series1: TLineSeries;

Series2: TLineSeries;

Series3: TLineSeries;

Button1: TButton;

procedure Button1Click(Sender: TObject) ;

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

implementation

{$R *. DFM}

procedure TForm1. Button1Click(Sender: TObject) ;

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

Ұқсас жұмыстар

DELPHI программалау жүйесі

Delphi –программалық ортасында бағдарламалау

Модель және модельдеу ұғымдары

Растрлік графика форматтары

Delphi ортасының графикалық мүмкіндіктері

Delphi ортасының мүмкіндіктері

Жоба терезенің астында

Электронды оқулық түсінігі

DELPHI БАҒДАРЛАМАСЫНДА ИНФОРМАТИКА ПӘНІНЕН ИНТЕРАКТИВТІ ТАПСЫРМАЛАР ЖАСАҚТАУ

Электрондық есептеуіш машинаның мүмкіндіктері

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz