Термодинамика және тасымалдау процестерінің негізгі ұғымдары мен анықтамалары


1 Негізгі ұғымдар және анықтамалар
1. 1 Физикалық құбылыстарды суреттеудің статистикалық және термодинамикалық әдістері
Молекулалардың жылулық (хаосты, бейберекет) қозғалысын суреттеу үшін физикада екі әдіс қолданылады: статистикалық және термодинамикалық. Жүйені статистикалық әдіспен суреттегенде қарастырылатын дене құрылысының қандай-да бір әлдебір моделі пайдаланылады. Термодинамикалық әдістің статистикалық әдістен айырмашылығы, ол құбылысты ең жалпы түрде бейнелейді, бұл әдісте заттың құрылысы мен құбылыстың молекула-кинетикалық механизмі туралы моделдік көзқарастар қолданбайды.
Сонымен бірге заттың ішкі құрылымы туралы терең білушілікті қажет етпей-ақ, әр түрлі заттардың тікелей бақыланатын сипаттамаларының арасындағы байланысты термодинамика тағайындайды. Бар жоғы бірнеше заңдарды және айнымалы шамаларды қолданып, ол орасан сан молекулалардан құралатын күрделі макроскоптық жүйелер туралы зор мәліметтер алуға мүмкіндік береді. «Бөлшектердің санының өте көптігінің» өлшемі ретінде, мысалы Авогадро санын
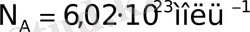
пайдаланады.
Құрамында өте көп бөлшектер болуынан макроскоптық жүйеде туындайтын заңдылықтарды статистикалық деп атайды. Бөлшектер саны соншалықты көи болмаған жүйелерде анықтама бойынша статистикалық заңдылықтардың күші жойылады.
Термодинамикалық әдістің тағы да бір артықшылығы - жан-жақтылығы, себебі оның тұжырымдамалары қарастырылатын жүйенің сипаттамаларынан тәуелсіз. Зат табиғатының ерекшеліктері бұл теорияда тек қана бірнеше параметр арқылы беріледі, мысалы мольдік шамалар және жылусыйымдылық сияқты. Екі әр түрлі күйлерде болатын жүйелердің әрекеттесуі туралы мәліметтерді термодинамикалық есептеулер арқылы алуға болады. Жылулық процестердің эксперименттік зерттеулерінің жалпы қорытындауы болатын осындай нәтижелердің жиынтығы термодинамиканың мазмұны болады.
Термодинамиканың негізгі ұғымдары мен заңдарының физикалық мағынасы статистикалық теория негізінде ашылады.
1. 2 Термодинамикалық тепе-теңдік. Тепе-теңсіздік шектеулер
Жүйені құрайтын барлық материялық нүктелердің жылдамдықтары және үдеулері нөлге тең күйі механикадағы тепе-теңдік күйді анықтайды. Сонда кез келген уақыт мезетінде әр нүктеге әрекет ететін тең әсерлі күш анықтама бойынша нөлге тең. Бұл шарттың бұзылуы механикалық тепе-теңдіктің бұзылуына әкеледі. Мұндай бұзылу мысалы ретінде, жүктеме астындағы металл үлгілерінің бүлінуін алуға болады.
Термодинамикалық тепе-теңдік ұғымының механикалық тепе-теңдікпен өзгешелігі мүлде баска сипатқа ие болады. Термодинамикалық жүйенің молекулалары (температура асқын төмен болмаса) теңдеспеген күштер әрекетінде болып жан-жақты мүмкін бағыттарда қозғалады. Термодинамикалық жүйе деп басқа денелермен және өзара энергия және (немесе) зат алмаса алатын бір немесе бірнеше денелер жиынтығын атайды. Мұнда тепе-теңдік ұғымды жүйені тұтас алғанда кейбір бірлескен (лат. collectivus - жинақтау, бірге, бірлескен, коллективтік) сипаттамаларына жатқызады, айталық, температура, қысым немесе компонент концентрациясы сияқты. Бұл сипаттамалар жүйе әрекеттерін макроскопты түрде бенелейді және күй параметрлері деп аталады. Белгілі сыртқы ортада орналасқан жүйені қарастырайық (1. 1 сурет) .
Егер алмасуға жауапты Xi және сыртқы ортаның Хe сипаттамаларының мәндері жүйе мен сыртқы ортада бірдей болса, онда жүйе термодинамикалық тепе-теңдік күйде болады. Айталық Хi - температураға сәйкес, жүйенің қабырғалары жылу өткізеді, сондықтан жүйе мен сыртқы орта энергиямен алмассын делік. Егер жүйенің кез келген нүктесінде және кез келген уақыт мезетінде Т=Тe, яғни температура теңдігі байқалады, онда жүйе мен сыртқы орта арасында термодинамикалық тепе-теңдік орнайды. Осыған ұқсас жағдай, егер жүйе сыртқы ортамен механикалық энергиямен алмаса алатын болса, онда механикалық тепе-теңдікте қысымдардың теңдігі орын алады, демек Р=Рe .
1. 1 сурет. Ашық жүйе
Егер жүйеге сыртқы күштер әсер етсе, онда термодинамикалық тепе-теңдікті сипаттайтын қосымша айнымалылар қажет болады.
Жоғарыда айтылғандар негізінде келесі қорытынды жасауға болады: егер оқшауланған жүйе термодинамикалық тепе-теңдікте болса, онда жүйенің барлық бөліктерінде қысым мен температура бірдей. Осы себептен тепе-теңдікте жүйенің әр түрлі бөліктерінің арасы термодинамикалық көмескі. Сыртқы ортамен энергия және зат алмаспайтын жүйені оқшауланған жүйе деп атайды.
Тепе-теңдік термодинамикасы екі іргелі заңға негізделген: термодинамиканың бірінші заңына немесе энергия сақталу заңына және екінші заңына немесе энтропия (гректің еn+trope - бұрылу, айналдыру) заңына. Тепе-теңдіксіз процестердің феноменологиялық теориясыда осы екі заңға негізделеді. Бірақ бұл жағдайда ол заңдар біраз басқа түрде тұжырымдалады.
Тепе-теңдік термодинамикасы жүйенің бұрынғы жайтын және оның бастапқы күйден соңғы күйге өту жолын ескермейді, бүны көрнекі түрде «осында және қазір» деп айтуға болады. Тепе-теңдік термодинамикасына қарағанда тепе-теңдіксіз процестер термодинамикасы материя дамуының динамикалық жайын қарастырады, солай болғандықтан ол тыныштық күй орнықпаған жүйені зерттейді. Тепе-теңдіксіз термодинамикасын тепе-теңдік термодинамиканың негізгі қағидаларын білмей түсінуге болмайды.
Кез келген термодинамикалық жүйелерге тән қасиет ретінде температура ұғымы термодинамикада нөлдік заң арқылы енгізіледі. Термодинамиканың нөлдік заңының тұжырымдамасы: егер екі А және В денелер бір-бірінен тәуелсіз және жеке-жеке үшінші С денемен жылулық тепе-теңдікте болса, онда олар бір-бірімен дәл сондай жылулық тепе-теңдікте болады; басқаша айтқанда жылулық тепе-теңдік жүйенің барлық нүктелерінде (бөліктерінде) температурасы тең болатынын анықтайды.
Термодинамиканың үшінші заңы да бар, оны Нернст заңы немесе жылулық теорема деп атайды. Бұл заңға сәйкес абсолют нөл температурада кез келген жүйенің энтропиясы нөлге тең болады.
1. 3 Термодинамиканың екінші бастамасы
Қайтымсыз процестердің ең өзіне тән ерекшеліктерін ғажайып дәл қамтыған 1865 ж. Рудольф Клаузиус тұжырымдаған түріндегі термодинамиканың екінші бастамасы. Клаузиус сыртқы ортамен не энергия, не масса алмаспайтын оқшауланған жүйелерді қарастырған. Мүндай жүйелер үшін Клаузиус бойынша, термодинамиканың екінші бастамасынан әлдебір S (энтропия) функциясы болатыны және ол өзінің максималды мәніне жеткенше термодинамикалық тепе-теңдік күйде монотонды өсіп отыратыны байқалады:
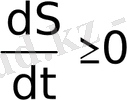 (1. 1)
(1. 1)
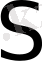 - экстенсивтік қасиетке жатады, демек, егер жүйе бірнеше бөліктерден құралса, онда жүйенің толық энтропиясы әр бөліктің энтропиясының қосындысына тең болады. Олай болса, энтропия - аддитивтік шама.
- экстенсивтік қасиетке жатады, демек, егер жүйе бірнеше бөліктерден құралса, онда жүйенің толық энтропиясы әр бөліктің энтропиясының қосындысына тең болады. Олай болса, энтропия - аддитивтік шама.
Клаузиус тұжырымдамасын сыртқы ортамен энергия және затпен алмасатын ашық жүйелерге де жинақтап қорытындылауға болады.
Мысалы, бұл айтылғандарды 1. 1 және 1. 2 суреттерде көрсетілген ашық жүйелерегі процестегі энтропия өсімшесінің қатысын талдау арқылы түсіндіруге болады. .
deS
1. 2 сурет. Ашық жүйе, мұндағы diS - .
энтропия өндірісі, deS - жүйенің сыртқы ортамен арасындағы энтропияның алмасуы
1. 2 суретте көрсеткендей, энтропия dS өсімшесінің екі құраушысын ажырату қажет: біріншісі deS жүйе шекарасынан энтропия тасымалдауын (сыртқы ортамен әсерлесуден туындайтын энтропия ағынын) суреттейді; екіншісі diS жүйеде өндірілген (жүйедегі ішкі өзгерістермен байланысты энтропия бөлігі) энтропияны белгілейді, сондықтан dS мына қосындыға тең болады:
 (1. 2)
(1. 2)
Ашық жүйенің оқшауланған жүйелерден айырмашылығы энтропияның dS өзгерісінде сыртқы ортамен алмасумен байланысты deS мүшенің болуы. diS мүше ешқашан теріс мәнді болмайды, ал deS мүшенің таңбасы сыртқы ортамен әрекеттесу түріне байланысты оң да, теріс те, нөл де болуы мүмкін.
Екінші бастамаға сәйкес қайтымсыз процестермен байланысты туындайтын жүйенің ішіндегі энтропия өндірісі оң мәнді, ешқашан теріс мәнді болмайды, яғни:
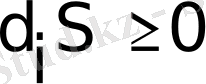 (1. 3)
(1. 3)
Мұндағы теңдік белгісі тепе-теңдік күйге сәйкес болады.
(1. 2. ) және (1. 3. ) өрнектер тұжырымдамасында қайтымсыз және қайтымды процестер айырмашылығын көрсететіні өте маңызды, яғни:
diS = 0 (қайтымды процестер) (1. 4)
diS > 0 (қайтымсыз процестер) (1. 5)
Егер deS = 0 болса, онда (1. 2) және (1. 3) салдарынан dS ≥ 0, бұл термодинамиканың екінші бастамасының жазылу түрі.
Қоршаған ортамен тек қана жылулық энергиямен алмаса алатын жабық жүйелер үшін, Карно-Клаузиус теоремасына сәйкес
deS =
 /T, (1. 6)
/T, (1. 6)
мұндағы dQ - сырттан жүйеге келетін жылу мөлшері, ал Т - осы жылуды қабылдайтын жүйенің температурасы.
Жабық жүйелер үшін (1. 2. ) және (1. 3. ) өрнектерден:
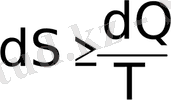 , (1. 7)
, (1. 7)
бұл термодинамиканың екінші бастамасының белгілі жазылу түрі.
Ашық жүйелер үшін (1. 2), (1. 3) теңдеулерді және deS =
 /T өрнекті қолдануға болмайды. Бірақ та (1. 2), (1. 3) өрнектердегі жалпы тұжырымдамалар дұрыстығы сақталады.
/T өрнекті қолдануға болмайды. Бірақ та (1. 2), (1. 3) өрнектердегі жалпы тұжырымдамалар дұрыстығы сақталады.
Энтропия өндірісіне тек қана қайтымсыз процестер үлес қосады. Бұндай процестерге химиялық реакциялар, диффузия, жылуөткізгіштік, тұтқырлық тағы да басқа процестерді жатқызуға болады.
Термодинамиканың екінші бастамасынан тағы да уақыттың бір бағыттылығы шығады; уақыттың оң бағытын екінші бастама энтропия өсуімен байланыстырады.
Ескерту. Оқшауланған жүйеде энтропия ағыны deS нөлге тең, сондықтан:
dS=diS≥0, deS=0. (1. 8)
Бұл (1. 8) өрнек энтропия ешқашан кемімейді деген термодинамиканың екінші бастамасының классикалық тұжырымдамасына сай және оның бұл қасиеті қайтымсыз процестер байқалуын анықтайтын критерийін береді.
Қайтымсыздықтың жалпы бірегей критерийі - ол (1. 4), (1. 5) өрнектерге сәйкес энтропияның өсуі.
1. 4 Кеңістік пен уақытты ірітүйірлі тегісте у
Оқшауланған жалпы жүйе I және II жүйелерден құралған болсын және де I-ші жүйе көлемі үлкендеу II жүйе ішінде орналассын, яғни I және II-ні жүйенің макроскоптық көлемшелері (жалпы жүйе көлемінің бөлшектерінің көлемдері) деуге болады.
Термодинамикалық тепе-теңдікте күй теңдеуі ортаның P қысымы, V көлемі, ρ тығыздығы сияқты негізгі параметрлерін: байланыстырады. Бұл макроскоптық параметрлерді бірмәнді түрде жүйенің микроскоптық сипаттамаларымен байланыстыруға болады, өйткені барлық макропараметрлер жүйенің тиісті микропараметрлерінің орташасы болып келеді. Мысалы, молекулалардың жылулық қозғалысының орташа энергиясымен температура байланысты, демек T∼m<v
2
>/2, ( мүндағы m -молекула массасы, <v
2
> - молекуланың орташа квадраттық жылдамдығы), ал тығыздығы
 , бөлшектердің n=N/V (мұндағы N-жүйедегі молекулалар саны, V-жүйенің көлемі) концентрациясымен анықталады.
, бөлшектердің n=N/V (мұндағы N-жүйедегі молекулалар саны, V-жүйенің көлемі) концентрациясымен анықталады.
Сірә, олай болса көлемшенің температурасы, тығыздығы, массалар центрі (ортасы) жылдамдығы және тағы да басқа шамалар туралы айтуға боладыы, және де бұл шамалар қарастырылатын көлемше бойынша орташалау арқылы табылады. Көлемше оқшауланған жүйе болмағандықтан, көлемше бойынша орташаларының жалпы жүйе бойынша орташадан айырмашылығы болуы мүмкін, яғни флуктуациялар байқалады, және де көлемшенің өлшемі неғұрлым кішірек болса, ауытқулар соғұрлым көбірек болады. Дегенмен жеткілікті ұзақ уақыт интервалында орташалағанда, бұл орташалар бүкіл жүйенің орташасымен бірдей болады. Сөйтіп, бір көлемшеден келесіге өткенде қандай болса да бір қасиеттің кеңістіктік біртексіздігі байқалады, демек осы қасиет координаттар мен уақыттың функциясы болады, мысалы,
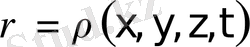 ,
,
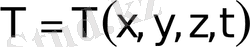 .
.
Егер заттың әйтеуір бір қасиетінің (P, T, ρ және т. б. макропараметрлерінің градиенті) кеңістіктік біртексіздігі туындаса, онда қайтымсыздық пайда болады. Толық тепе-теңдік орнығу үшін, кез келген қайтымсыз процесс өз қасиетін тегістеуге тырысады. Айта кететін жағдай, мұндай қарастырғанда x, y, z - координаттық остің нүктелері емес, бұлар жалпы жүйенің көлеміндегі N бөлшектер санынан әлдеғайда кіші, Ni бөлшегі бар, көлемшенің сипаттамалары болады. Сөйтіп, мұндай координаттар гидродинамикалық масштабты координаттар деп аталады.
Заттың қасиетінің кеңістіктік біртексіздігінде өмір сүру немесе тарауы уақыты бойынша ажыратылатын ұсақ және ірі масштабты флуктуациялар байқалады. Егер ұзақ уақыт аралығында орташаласақ, онда флуктуациялар өзара бір-бірін жояды, сонда біз флуктуация сезілмейтін орташа ерекше уақытты анықтаймыз, яғни уақыт шкаласы интервалдарға бөлінеді.
Осылай біз кейбір көлемше мен уақыт шкаласындағы белгілі уақыт интервалына қатысты локалды макросипаттамалар ұғымына келеміз (1. 3 сурет) :
х1 х2 х3 хn
x, t
t1 t2 t3 tn
1. 3 сурет
Сонымен қандай да бір макропроцесс қарастырылғанда, уақыттың ерекше (сипаттамалық) интервалы (масштабы) туралы ұғым енгізіледі. Қарастырылатын процесте жүйенің өзгеретін қасиеті байқалатын уақыт интервалын сипаттамалық уақыт масштабы деп атайды. .
Қарастырылатын процестің сипаттамалық уақыт масштабынан өмір сүру уақыты анағұрлым кіші болатын флуктуацияларды үсақ масштабты флуктуациялар дейді. Сонымен, локалды кеңістік аймақтары және уақыт интервалын бейнелеуші гидродинамикалық кеңістіктік координаттық жүйесі
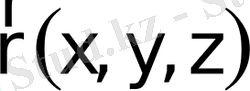 және гидродинамикалық уақыт масштабы
және гидродинамикалық уақыт масштабы
 локалды кеңістік аймақтары және уақыт интервалы әр ρ, T, p және т. б. макропараметрлердің бір жалпы мәнімен сипатталады. Басқаша айтқанда, болжау бойынша орташалағанда ұсақ масштабты флуктуациялар жойылған кеңістік және уақыт интервалдарын
локалды кеңістік аймақтары және уақыт интервалы әр ρ, T, p және т. б. макропараметрлердің бір жалпы мәнімен сипатталады. Басқаша айтқанда, болжау бойынша орташалағанда ұсақ масштабты флуктуациялар жойылған кеңістік және уақыт интервалдарын
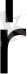 және
және
 бейнелейді.
бейнелейді.
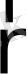 бейнелейтін локалды аймақ элементар физикалық көлем (ЭФК) деп аталады. Осындай кеңістік координаттар және уақыт жүйесін енгізуді кеңістік пен уақытты ірітүйірлі тегістеу деп атайды.
бейнелейтін локалды аймақ элементар физикалық көлем (ЭФК) деп аталады. Осындай кеңістік координаттар және уақыт жүйесін енгізуді кеңістік пен уақытты ірітүйірлі тегістеу деп атайды.
Егер әр түрлі ЭФК-де жүйенің бір немесе бірнеше параметрлері (Р, Т, ρ және т. б. ) әр түрлі мәнді болса, онда жүйе тепе-теңдіксіз күйде болады.
Егер ЭФК-дегі макропараметрлердің мәндері барлық тұтас оқшауланған жүйе бойынша орташасының мәндерінен айырылатын болса, онда ірімасштабты флуктуациялар байқалады.
Біз үзіліссіз жүйелерді қарастырамыз, оларда бір ЭФК--нен келесісіне өткенде заттың қасиеттерінің өзгерісі қатты емес, сондықтан гидродинамикалық масштабтағы кеңістік координаттары мен уақытты үзіліссіз шамалар деп есептеуге болады. Бұл жағдайда жүйенің макроқасиеттерін (Р, Т, ρ және т. б. ) гидродинамикалық масштабтағы кеңістіктік координаттары және уақыттың үзіліссіз функциялары деп қарастыруға болады.
1. 5 Ағындар және қайнар көздері туралы ұғым
Тасымалдау процестерін суреттегенде ағын (масса, импульс, энергия, зарядтың және т. б. ) ұғымы қолданылады.
Берілген бет арқылы бірлік уақытта массаның тасымалдауын J масса ағыны деп атайды. Көпкомпоненттік жүйе үшін жеке Jі компоненттің ағын шамаларын білу керек. Масса ағыны белгіленген бет арқылы заттың тасымалдауын сипаттайды, ал бет елес, жалған (фиктивті) да түрінде болуы мүмкін.
Егер J=0 болса, онда жүйе тыныштықта бола ма? Тыныштықтағы жүйе үшін
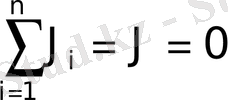 ,
,
яғни толық ағын нөлге тең. Кері пікір дұрыс емес, J - интегралдық ағын, демек интегралдық шама және жүйенің жеке бөліктерінде тиісті ағын болса да, нөлге тең болуы мүмкін («бір құбырдан шығады, екіншіге кіреді») .
Меншікті ағын (ағынның беттік тығыздығы)
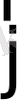 бірлік беттіен өтетін ағын, бұл жағдайда
бірлік беттіен өтетін ағын, бұл жағдайда
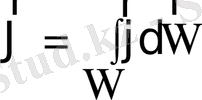 , (1. 9)
, (1. 9)
мұндағы
 -бет элементі,
-бет элементі,
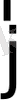 - координаттар және уақытқа тәуелді және ерекше көңід аударатын жайт, ол қарастыратын ауданның бағытына байланысты, яғни
- координаттар және уақытқа тәуелді және ерекше көңід аударатын жайт, ол қарастыратын ауданның бағытына байланысты, яғни
 ,
,
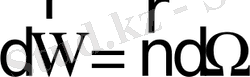 ,
,
мұндағы
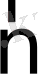 - сыртқы бірлік нормаль.
- сыртқы бірлік нормаль.
Айтылғанның бәрі жылу, яғни энергия ағынына да қатысты. Термодинамикалық тепе-теңдік маңайында (локалды квазитепе-теңдік) жүйелердің алмасатын энергиясы жылу ұғымымен, ал меншікті заряд ағыны- электр тогының тығыздығымен (заряд ағыны, демек электр ағыны, ол ток күші) теңдестіріледі. Импульс векторлық шама болғандықтан, берілген бет арқылы импульстің Пx, Пy, Пz үш бағытта ағыны болады, осылардың әрбірі берілген бет арқылы бірлік уақытта өтетін импульс проекциясының шамасын көрсетеді. Онда импульстың 3 меншікті ағыны πх, πһ, πz бар, оның әрбіреуі элементар dS ауданның бағытталуына тәуелді. Егер dS аудан x, y, z осьтеріне перпендикуляр бағытталған болса, онда әрбір πi-де үш πiх, πiy, πiz компоненттерге ие болады. Сөйтіп, импульс ағыны 9 компонентті (9 бағытты) шама, демек осы жиынтығы импульстың меншікті ағын тензорын құрастырады:
πххπхуπхz
П= πyхπyyπyz`
πzхπzyπzz
Импульстың сақталу заңы бойынша, Ньютонның екінші заңына сәйкес, дененің көлемінің ішіндегі бірлік уақыттағы импульстің өзгерісі денеге сұйық жағынан әрекет ететін тең әсерлі күшке тең болуы керек. Жеңілдету үшін і - компонентін қарастырайық. Дененің бетінде бұл күш нөлге тең болмайды, сондықтан
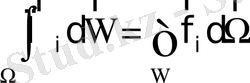 ,
,
мұндағы Пik=fik, fik, -беттік күш, сондықтан импульс ағыны беттік күшпен баламалы шама. Гидродинамикада fik, - кернеу ретінле түсіндіріледі. Осыдан Пik=_- Рik, мұндағы Рik - кернеу тензоры деп аталады.
Ескерту. Ағындарды макроскопты және микроскопты деңгейде суреттеуге болады. Макроскоптық моделде газ континуум (латынша сontinuum - үзіліссіз) ретінде қарастырылады және тиісті суреттеуі макроскоптық жылдамдық, тығыздық, қысым және температураның координаттар мен уақыттан тәуелділігі арқылы беріледі. Микроскоптық немесе молекулалық модель газдың құрылымын сансыз дискретті молекулалар жиынтығы ретінде қарап, кез келген уақыт мезетінде барлық молекулалардың орны және жылдамдығы туралы мәліметтерді қамтамасыз етеді. Бірақ мұндай атомдық-молекулалық суреттеменің практикалық қажеттілігі шамалы. Сондықтан ағындар, мысалы газдың, макроскоптық шамалар арқылы суреттеледі. Кіріспеде айтылғандай, ағынның кез келген нүктесіндегі макроскоптық шамалар тиісті молекулалық шамалардың орташаларымен теңдестіріледі. Ал континуалдық суреттеме дұрыс болу үшін физикалық элементар көлемде (ЭФК) орташаларды анықтауға жеткілікті молекулалар саны болуы керек. Сондықтан, бұл екі моделдің айырмашылығы жүйені феноменологиялық және статистикалық бейнелеуінде, жүйенің табиғатына байланысы жоқ. Осы оқу құралында макроскоптық лөзқарас пайдаланады.
Тасымалдау құбылыстар теориясында жалпы мағынада қарастырылатын шаманың (масса, импульс, жылу, . . . ) қайнар көзі деп, осы шама ағындары болмағанда, жүйеде өтетін ішкі процестер есебінен болатын, шама өзгерісінің себебін атайды.
Жүйедегі қайсыбір компоненттің массасының қайнар көзі ретінде химиялық және ядролық реакциялар, диссоция және ионизация процестері және т. б. болуы мүмкін. Жылудың қайнар көзі ретінде джоуль жылуы, реакция жылуы және т. б. жылулары алынуы мүмкін.
Бірлік көлемде бірлік уақытга туындайтын i-компоненттің массасының шамасын қайнар көзінің қуаты деп айтады. Қуаттың таңбасы теріс болса, демек i-компоненттің массасы жүйеге ағып келетін (кіретін) болса, оны ағу көзі (орыстың сток - ағу) деп атайды.
ЭФК-де қайсыбір қасиеттің өзгерісінің екі себебі болуы мүмкін:
1) бет арқылы қасиеттің ағыны пайда болуы;
2) көлемдік қайнар көздерінің әрекеті.
Тепе-теңдіктегі жүйенің тарихы болмайды және уақытта ескерусіз қалады, демек ол «жансыз жүйе» болады.
2. 1 Сақталу заңдарының жалпы түрі
Қайсыбір қасиетінің кеңістіктік біртексіздігі болатын жүйелер үшін сақталу заңдарын баланс теңдеулері деп атайды.
Массаның, зарядтың, толық энергияның, импульстың және т. б. сақталу заңдарыболады. Көлемнің
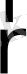 нүктесінің төңірегінде
нүктесінің төңірегінде
 ЭФК-де
ЭФК-де
 уақыт мезетінде қандай да бір
уақыт мезетінде қандай да бір
 (
(
 ,
,
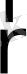 ) экстенсивтік қасиеттерінің кез келгенін қарастырайық. Осы
) экстенсивтік қасиеттерінің кез келгенін қарастырайық. Осы
 (
(
 ,
,
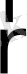 ) қасиеттің тығыздығын
) қасиеттің тығыздығын
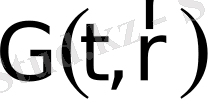 деп белгілейік, ол мынадай қатынас бойынша анықталады:
деп белгілейік, ол мынадай қатынас бойынша анықталады:
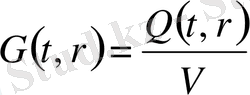 , (2. 1)
, (2. 1)
Мұндағы
 (
(
 ,
,
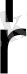 ) жүйенің V еркінше (қалай болса солай) алынған толық көлемінің бөлігіндегі қасиет мөлшері. Онда V көлемдегі қасиеттің мөлшері мынаған тең болады:
) жүйенің V еркінше (қалай болса солай) алынған толық көлемінің бөлігіндегі қасиет мөлшері. Онда V көлемдегі қасиеттің мөлшері мынаған тең болады:
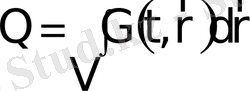 , (2. 2)
, (2. 2)
мұндағы
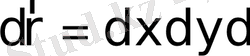 - элементар физикалық көлемі (ЭФК) .
- элементар физикалық көлемі (ЭФК) .
ЭФК нің Ω беті арқылы қасиеттің «ағып келуі» немесе «ағып кетуі» есебінен
 (
(
 ,
,
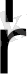 ) өзгеруі мүмкін, бұл жағдай
) өзгеруі мүмкін, бұл жағдай
 (
(
 ,
,
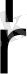 ) қасиет мөлшерінің dQ/dt ағынын тудырады. (2. 1 сурет) .
) қасиет мөлшерінің dQ/dt ағынын тудырады. (2. 1 сурет) .

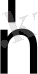
м
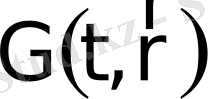 қасиеттің ағыны тығыздығын
қасиеттің ағыны тығыздығын
 деп белгілейік.
деп белгілейік.
 Ағынның анықтамасы векторлық алгебрадан белгілі. Егер қасиеттің ағып кетуінің бағыты
Ағынның анықтамасы векторлық алгебрадан белгілі. Егер қасиеттің ағып кетуінің бағыты
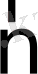 сыртқы нормаль бағытына 2. 1 сурет сәйкес болса, онда ЭФК-де
сыртқы нормаль бағытына 2. 1 сурет сәйкес болса, онда ЭФК-де
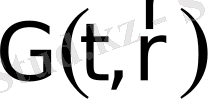 кемиді, сондықтан
кемиді, сондықтан
таңбасы «минус» ал керісінше өсетін болса, онда «плюс» таңбамен алынады (2. 1 сурет) . Сондықтан былай белгілеуге болады:
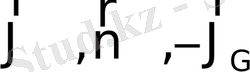 ;
;
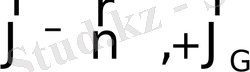 . Осыған орай
. Осыған орай
 (
(
 ,
,
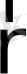 ) қасиеттің өзгеру жылдамдығы былай жазылады:
) қасиеттің өзгеру жылдамдығы былай жазылады:
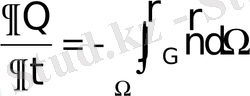 . (2. 3)
. (2. 3)
(2. 3) өрнек
 (
(
 ,
,
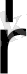 ) қасиеттің сақталу заңының интегралдық түрі болады, мұндағы
) қасиеттің сақталу заңының интегралдық түрі болады, мұндағы
 -
-
 бетке түсірілген сыртқы нормаль (2. 1 сурет) .
бетке түсірілген сыртқы нормаль (2. 1 сурет) .
Остроградский-Гаусс теоремасы бойынша (көлемдік интегралды беттікке түрлендіру)
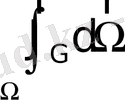
шама
 нүктесін қоршаған және
нүктесін қоршаған және
 көлемімен бірге
көлемімен бірге
 аймақты қапсыратын тұйық
аймақты қапсыратын тұйық
 беті арқылы өтетін векторлық өрістің скаляр ағыны (2. 1 сурет) болады. Остроградский-Гаусс теоремасын қолданып, (2. 3) беттік интегралын көлемдікке түрлендірсек, онда (2. 3) теңдеуін төмендегіше жазуға болады:
беті арқылы өтетін векторлық өрістің скаляр ағыны (2. 1 сурет) болады. Остроградский-Гаусс теоремасын қолданып, (2. 3) беттік интегралын көлемдікке түрлендірсек, онда (2. 3) теңдеуін төмендегіше жазуға болады:
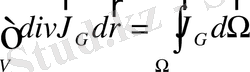 (2. 4)
(2. 4)
(2. 2) және (2. 4) өрнектерін ескеріп, (2. 3) өрнекті былай жазуға болады:
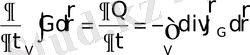 (2. 5)
(2. 5)
Көлемнің
 шамасын еркімен алуға болатындықтан,
шамасын еркімен алуға болатындықтан,
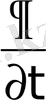 -дифференциалдау және ∫ -интегралдау таңбаларының орынын ауыстыруға болатынын ескеріп,
-дифференциалдау және ∫ -интегралдау таңбаларының орынын ауыстыруға болатынын ескеріп,
Мынаны аламыз:
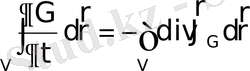 (2. 6)
(2. 6)
Осыдан V көлемде қайнар көздері мен ағу көздері жоқта,
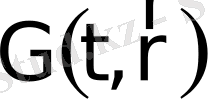 қасиет тығыздығының сақталу заңының дифференциалдық түрі былай жазылады:
қасиет тығыздығының сақталу заңының дифференциалдық түрі былай жазылады:
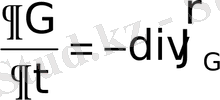 (2. 7)
(2. 7)
Осы өрнектен
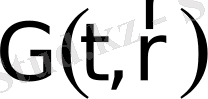 қасиеттің ағыны тығыздығының өлшем бірлігі былай анықталады:
қасиеттің ағыны тығыздығының өлшем бірлігі былай анықталады:
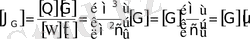 (2. 8)
(2. 8)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz