Ірі құйындар әдісімен пішіндеу: фильтрленген Навье-Стокс теңдеулерін торлы модельдеу және сандық шешу алгоритмдері


Әл- Фараби атындағы Қазақ Ұлттық университеті
Механика-математика факультеті
Компьютерлік және есептеуіш технологиялары кафедрасы
бІТІРУ жұмысы
Ірі құындар әдісімен пішіндеу
Ғылыми жетекші
т. ғ. д., профессор, академик
Нормақадағалаушы
“__”2009 ж.
Кафедра меңгерушісінің рұқсатымен қорғауға жіберілді
ф. -м. ғ. д., профессор
Алматы, 2009
МАЗМҰНЫ
КІРІСПЕ
Турбуленттік қозғалыс табиғатта және техникалық құрылғыларда газдар мен сұйықтықтар түріндегі қозғалыстарының өте кең таралған формалары болып табылады. Жыл сайынғы басылымдарда турбуленттік зерттеулердің ғасырлар бойында жинақталған зерттеулерінің осы бағытта жасалған еңбектері турбуленттік ағымның қанағаттанарлық есептеу әдісінің жоқ екенін көрсетіліп келеді. Бұл екі түрлі себептермен түсіндіріледі:
Құбылыстың жалпы өзіндік күрделігі бар;
Қәзіргі қолданыстағы жүрген құйын теориясының бағытының шектеулі мүмкіндігі;
Турбуле́нттік , турбуле́нция (лат. turbulentus - құйынды, ашулы), турбуленттік ағым - құбылыс. Рейнолдьс және Релей сандарының келеңсіз асып кету салдарынан өз-өздігінен көптеген сандық емес фрактальді тербелістер және әр түрлі көлемдегі жай сыртқы көзге көрінбейтін айналадағы кеңістікке өз әсерін тигізбей қоймайтын құбылыс. Осы құйындарды есептеу үшін де әр түрлі құйын моделі ойластырылған.
Турбуленттікті ағылшын инженері Рейнолдьс 1883 жылы трубаларда судың жиналмауын анықтап жатқанда ашқан.
Турбуленттіктің пайда болуы үшін Новье-Стокс немесе Больцманның кинетикалық теңдеуіне тәуелді немесе шекаралық қабатты толық орта қажет. Новье-Стокс теңдеуі тәжірибеде көптеген нақты турбуленттікті анықтап береді. Нақты айтсақ көптеген газдарда және сұйықтықтарда, көпфазалық ағымдарда, сұйық кристалдарда, плазмаларда кездеседі (мысалы, құмда, жерде, металлда) . Турбуленттік тағы жұлдыздардың атылуында, адамның өкпесінде, жүректегі қанның ағымында байқалады. Олар қысымның түсуінен немесе күштің ауырлауынан немесе екі ортаның бірге келуінен және бір - бірімен жанаса өтуінен пайда болады. Ол кездейсоқ күштердің пайда болуынан шығуы мүмкін. Әдетте сырттқы кездейсоқ күш және ауырлық күші бірге әсер етеді. Мысалы, жерсілкінісі немесе қатты жел түрганда таудан сел жүреді. Мұнда қар ағымында құйын кездеседі. Турбуленнтік бұл жеке сақталған импульстердің туындысының және Навье-Стокс массасының сақталуы және энергия теңдеуінің кейбір Рейнольдс санының асуы болып келеді. Ол өзіндік қасиеті бар фрактальді және сызықты емес ағымдарды білдіреді. Өте аз мөлшерде Рейнольдс саны бұл барлығына белгілі судағы сызықты толқындар.
Қазіргі уақыттағы тұтас орта механикасының және плазма физикасының актуалды проблемаларының бірі - дамыған есептеуіш техникалар, алгоритмдер және қолданбалы математиканың әдістері арқылы күрделі ауыспалы және турбулентті қозғалыстарды пішіндеу болып табылады. Тәжірибе кезінде ең көп кездесетін турбуленттік ағыстар орындалып жатқан процестердің стационарсыздығымен және сызықсыздығымен, ортаның күрделі өзгерісімен, әртүрлі сипаттарымен өзара әрекеттесудің күрделі механизмімен және энергия диссипациясымен ерекшеленеді. Бұған мысал ретінде кейбір газодинамикалық проблемаларды келтіруге болады, мысалы жылжымалы дененің ізімен қозғалатын ағыстың есебі және т. б.
Турбуленттік теорияның негізгі мақсаты - турбуленттіліктің даму қасиеттері мен жалпы динамикасын зерттеу, яғни ірі масштабты структуралардың пайда болу эволюциясы мен уақыт ағысын қоса есептегендегі турбуленттік қозғалыстың статистикалық көрінісін зерттеу.
Турбуленттік қозғалыс ламинарлық ағыстың орнықсыздылығынан пайда болады және оның характері ағыстың геометриясымен анықталады. Орнықсыздылық әсерінен негізгі ағыннан энергияны жұтатын толқын сияқты структуралар пайда болады. Структуралар саны өскен сайын энергия ауытқулардың басқа түрлеріне беріле бастайды да, соның салдарынан турбуленттіліктің пайда болуына әсер ететін ретсіз пульсациялар пайда болады.
Толығымен дамыған турбуленттіліктің характеристикасы оның пайда болу қасиетін көрсетеді. Турбуленттіліктің сақталуы үшін энергияның үздіксіз жеткізілуі керек болғандықтан турбуленттік структуралар негізгі ағыннан энергияны үздіксіз жұтуы керек Соңғысының характеристикалары турбуленттіліктің әсерінен өзгеріп, сонымен қоса энергияны жұтатын структуралар турбуленттілікті тудыратын структуралармен ұқсастығы болады.
Осылай турбуленттік ағыстағы ірі масштабты структуралар негізгі ағындағы энергияны жұтады. Осының арқасында олар күшті анизотропты, құйынды және оңай айрықшаланатын болады, және де олар әсіресе көп жағдайларда турбуленттік ағыстағы тасымалдау процессінің характерін анықтайды. Сонымен қатар, энергия генерациясының негізгі механизмі құйындар деформациясы болып табылады. Сызықсыз әрекеттесудің әсерінен ірі масштабты структуралар өзінің энергиясының бір бөлігін кіші масштабты структураларға береді. Бұл кіші масштабты структуралардың негізгі функциясы ірі масштабты структураларға жеткізілетін энергия диссипациясы. Сонымен қоса кіші масштабты структуралардың характеристикасы өзінде таралатын энергияның мөлшерімен анықталатыны анық. Осы себептен олар ірі масштабты структураларға қарағанда универсалды болады.
Кіші масштабты структуралардың өзіне сәйкес өлшемдері негізгі ағынның геометриясына ешқандай байланысы болмайды, сондықтан ол тек тұтқырлық арқылы және ірі масштабты структуралардан келетін энергия диссипациясы арқылы анықталады.
Колмогоровтың масштабтар жайлы анализіне сәйкес
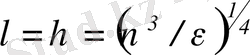 , және осындай өлшеммен құйынға келетін энергия келесі теңдеумен өзгереді.
, және осындай өлшеммен құйынға келетін энергия келесі теңдеумен өзгереді.
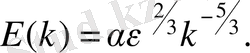 (1)
(1)
Мұндағы
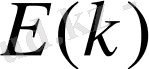 - келесі теңдікті қағанаттандыратын энергия тығыздығының үш өлшемді спектрі,
- келесі теңдікті қағанаттандыратын энергия тығыздығының үш өлшемді спектрі,
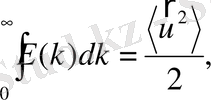
ал
 - Колмогоров тұрақтысы.
- Колмогоров тұрақтысы.
Мұндай энергияның спектральды таралуы толқын санының өзгеруінің инерциялық аймағында кездеседі, яғни
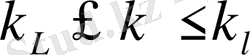 диапазонындағы
диапазонындағы
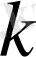 толқын саны үшін орынды, мұндағы
толқын саны үшін орынды, мұндағы
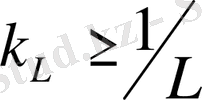 және
және
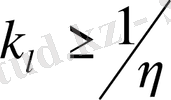 .
.
Каскадты процесстің маңызды қасиеттерінің бірі энергияның ірі масштабты құйындардан кіші масштабты құйындарға таралуының жалғыздығы болып табылады. Каскадты процесстің келесі маңызды қасиеттерінің бірі ірі масштабты(толқын сандары кіші) құйындардың кезкелген кеңістіктік ориентациясы кіші масштабты(толқын саны үлкен) құйындарға өту кезінде жоғалады, сондықтан кіші масштабты турбуленттілікті жергілікті изотропты деп қарастыруға болады.
Турбуленттіліктің жоғарыда аталған универсальды қасиеттеріне сүйене отырып, есептеуіш тордың қадамынан кіші масштабтар арқылы турбуленттіліктің моделін құруға болады. Бұл модельге кіретін жалғыз эмпирикалық тұрақты импульстің тасымалдануын сипаттайтын
 Колмогоров тұрақтысы болады. Дегенмен мұндай универсальды заңдылықтар тек өте үлкен Рейнольдс сандарында орындалады, сондықтан есептеуіш тордың қадамынан кіші масштабтар арқылы табылған турбуленттілік моделдің спектральды қасиеттерге негізделген қолданылымы Рейнольдс саны кеміген сайын тарылады.
Колмогоров тұрақтысы болады. Дегенмен мұндай универсальды заңдылықтар тек өте үлкен Рейнольдс сандарында орындалады, сондықтан есептеуіш тордың қадамынан кіші масштабтар арқылы табылған турбуленттілік моделдің спектральды қасиеттерге негізделген қолданылымы Рейнольдс саны кеміген сайын тарылады.
1 Ірі құйындар әдісімен пішіндеу
Үлкен масштабты турбуленттік теңдеуді алу үшін әртүрлі теңдеулер қажет. Турбулентті ағыстарды есептеудің сандық әдістерінің ішінен ерекше атап өтуге болатындары тікелей сандық пішіндеу мен орташаланған Навье-Стокс теңдеуін шешу. Тікелей сандық пішіндеуді қолдану үшін қарқынды есептеуіш ресурстары қажет. Ал орташаланған Навье-Стокс теңдеуін шешу үшін қарқынды есептеуіш ресурстары көп қажет болмаса да, теңдеуді тұйықтау үшін қолданылатын турбуленттік модель қолданбалы есептердің барлық түрлеріне қолданыла алмайды.
Ірі құйындар әдісімен пішіндеу тікелей сандық пішіндеу мен орташаланған Навье-Стокс теңдеуін шешу арасындағы компромиссті түрі. Ірі құйындар әдісімен пішіндеуде кеңістік бойынша фильтрленген Навье-Стокс теңдеуі шешіледі.
Әдіс екі мүмкін болатын жағдайларға негізделген. Бірінші жағдайда жылдамдықтар өрісін ірі және кіші құйындар қозғалысына бөлу мүмкіндігі, мұнда кіші құйындардың универсальдығы мен изотроптығына сүйене отырып ірі құйындар қозғалысын бөлек есептеуімізге болады. Екінші жағдайда торлы модельді пайдаланып ірі және кіші құйындар арасындағы сызықсыз әрекеттесуді тек ірі құйындар бойынша аппроксимациялау.
Сонымен қорытындысында Навье - Стокс теңдеуіне фильтр операциясын пайдаланып және торлы модель арқылы пішінделеді . Фильтр функциясының ішіндегі ең көп кездесетіндері - Гаусс, Фурье және цилиндрлік фильтрлері. Ал торлы модельдердің ішінен ерекше атап өтуге болатындары Смагоринский моделі, екінүктелік тұйықтау моделдері, динамикалық модельдер және масштабтардың ұқсастық модельдері.
Ірі масштабты қозғалыстар фильтрленген стацианар емес Навье-Стокс теңдеулер жүйесінен есептелінеді.
Ірі құйындар әдісі - бұл айқын түрде ірі масштабты турбулентті структуралардың эволюциялық есептеуі жүргізілетін және кіші масштабты структуралар пішінделетін сандық әдістің түрі.
Турбуленттік ағыстың есептеуі Навье-Стокс теңдеуінің негізінде жүргізіледі
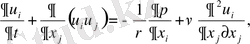 (1. 1)
(1. 1)
және үзіліссіздік теңдеуі
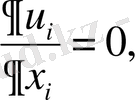 (1. 2)
(1. 2)
мұнда қайталанатын индекс бойынша қосынды ережесі орындалады.
Ірі құйындар әдісінің негізгі идеясы ірі және кіші құйындарды математикалық бөлу, оны кеңістік бойынша орташалау арқылы іске асыру, яғни фильтр арқылы ірі масштабты пульсациялар өрісін анықтау.
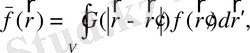 (1. 3)
(1. 3)
мұндағы
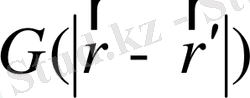 - фильтр функциясы.
- фильтр функциясы.
Фильтрді айқындайтын әртүрлі әдістер бар:
-«қорап» түріндегі фильтр
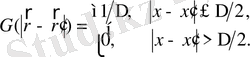 (1. 4)
(1. 4)
-Фурье фильтрі
(1. 5)
-Гаусс фильтрі
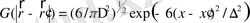 (1. 6)
(1. 6)
Фильтрлеудің көмегімен, яғни Гаусс фильтрі арқылы келесі орташаланған Навье-Стокс теңдеуін аламыз
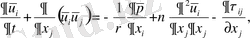 (1. 7)
(1. 7)
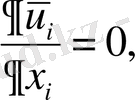 (1. 8)
(1. 8)
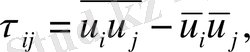 (1. 9)
(1. 9)
мұндағы
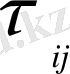 - пішінделетін кіші масштабты структураларға жауапты торлы мүше.
- пішінделетін кіші масштабты структураларға жауапты торлы мүше.
Ірі құйындар әдісінің мақсаты - турбуленттіліктің торлы масштабтарының қозғалысын нақты анықтау. Турбуленттіліктің торлы масштабтарының әсері торлы мүше арқылы айқындалады.
Торлы масштаб моделінің негізгі ролі шешілген масштабтардан энергияны жою. Сондықтан торлы модель торлы мүшені шешпейді, керісінше оның статистикалық мәнінің әсерін көрсетеді. Көптеген модельдер орташаланған Навье-Стокс теңдеуінде қолданылатын құйындық тұтқырлықтың түсінігіне негізделген.
Смагоринский моделі
Турбулентті торлы модельдердің ішіндегі жиі қолданылатыны келесі түрде берілетін Смагоринский моделі
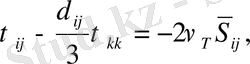 Equation. 3 (1. 10)
Equation. 3 (1. 10)
мұндағы
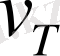 Equation. 3 - турбуленттік тұтқырлық және ол мынаған тең:
Equation. 3 - турбуленттік тұтқырлық және ол мынаған тең:
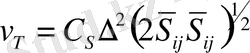 Equation. 3 ;
Equation. 3 ;
 Equation. 3 - ағынның характеріне тәуелді коэффициент;
Equation. 3 - ағынның характеріне тәуелді коэффициент;
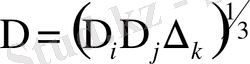 - торлы фильтрдің ені;
- торлы фильтрдің ені;
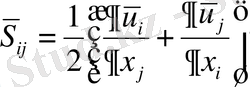 - деформация жылдамдықтарының тензорлық өлшемі.
- деформация жылдамдықтарының тензорлық өлшемі.
Бұл модель кең танымал болғанымен мынадай кемшіліктері бар:
- ағынға тәуелді болатын модельдіңкіріс коэффициентін табу керек;
- қабырғада немесе ламинарлық ағында қозғалыстың корректті емес асимптотикалық өзгерісін сиппатайды;
- кіші құйындардың энергиясын ірі құйындарға кері таралуын болдырмайды;
- торлы структуралардың кернеулер тензорының басты осі деформация жылдамдықтар тензорымен түзуленетінін жобалайды;
- Смагоринский моделі ауыспалы ағынның шекарасында диссипативті.
- Негізгі теңдеулерді шешу алгоритміНегізгі теңдеулер
Турбулентті ағыстың негізгі теңдеулері орташаланған Навье-Стокс пен үзіліссіздік теңдеуімен беріледі .
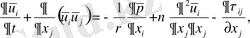 (2. 1. 1)
(2. 1. 1)
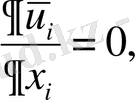 (2. 1. 2)
(2. 1. 2)
Бұл жұмыста торлы кернеулерді пішіндеу үшін Смагоринский моделі қолданылады:
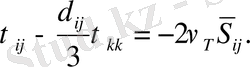 (2. 1. 3)
(2. 1. 3)
- Теңдеуді өлшемсіз түрге келтіру
Теңдеуді өлшемсіз түрге келтіру үшін жылдамдықтың
 , ұзындықтың
, ұзындықтың
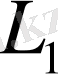 , енінің
, енінің
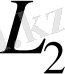 және биіктіктің
және биіктіктің
 кейбір характерлік шамаларын таңдаймыз.
кейбір характерлік шамаларын таңдаймыз.
Берілген мәндерді пайдаланып, келесі белгілеулерді енгіземіз:
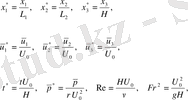 (2. 2. 1)
(2. 2. 1)
мұндағы
 - Рейнольдс саны, ал
- Рейнольдс саны, ал
 - Фруд саны.
- Фруд саны.
Жылдамдықтың көлденең құраушысы u 1 үшін теңдеуді қарастырайық.
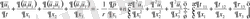
Өлшемсіз шамаларды қоя отырып келесі теңдеуді аламыз(орташаланған белгіні түсіріп тастаймыз) :
 (2. 2. 2)
(2. 2. 2)
Енді жылдамдықтың көлденең құраушысы u 2 үшін теңдеуді қарастырайық .
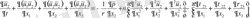
Өлшемсіз шамаларды қоя отырып келесі теңдеуді аламыз:
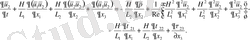 Equation. 3
(2. 2. 3)
Equation. 3
(2. 2. 3)
Енді жылдамдықтың тік құраушысы u 3 үшін теңдеуді қарастырайық .
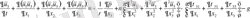
Өлшемсіз шамаларды қоя отырып келесі теңдеуді аламыз:
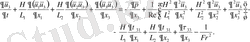 Equation. 3
(2. 2. 3)
Equation. 3
(2. 2. 3)
Өлшемсіз шамаларды үзіліссіздік теңдеуге қойсақ алатынымыз:
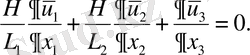 (2. 2. 4)
(2. 2. 4)
- Сандық алгоритм
Турбуленттік ағыстарды шешу үшін физикалық параметрлер бойынша ыдырау әдісінің схемасын қолданамыз:
- (2. 3. 1)
- (2. 3. 2)
- (2. 3. 3)
Ыдырау әдісінің келесі физикалық интерпpетациясы ұсынылады. Бірінші сатыда қозғалыс көлемінің таралуы конвекция мен диффузия арқасында жүзеге асады. Сондықтан аралық жылдамдықтар өрісі бөлшектік қадам әдісімен шешіледі.
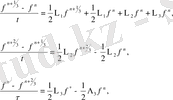 (2. 3. 4)
(2. 3. 4)
мұндағы операторлар келесі түрде жазылады:
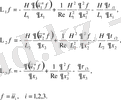 (2. 3. 5)
(2. 3. 5)
Аралық жылдамдықтар өрісінің мәндерін әрбір бағытта есептеу үшін беснүктелік қуалау әдісін қолданамыз.
Екінші сатыда табылған аралық жылдамдықтар өрісі арқылы қысым өрісі анықталады. Қысым өрісі үшін жазылған Пуассон теңдеуі Фурье әдісімен шешіледі.
Үшінші сатыда таралу қысым градиентіне байланысты орындалады деп қарастырамыз.
Қорытындысында есептеу циклі келесі түрде болады:
- (2. 3. 1) теңдеуіндегі уақыттың бастапқы моментіндегі жылдамдықтар өрісі арқылы (2. 3. 2) теңдеудің оң жағын анықтай отырып аралық жылдамдықтар өрісін анықтаймыз;
- қысымды анықтау үшін Пуассон теңдеуі шешіледі;
- Қысым градиентінің көмегімен ақырлы жылдамдықтар өрісі толықтырылады .
Цикл берілген уақыт моментіне дейін жалғаса береді.
Зерттеліп жатқан ағыстың аймағы кеңістік бойынша тордың ұяшығымен тегіс жабылады
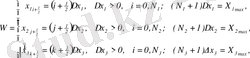 (2. 3. 6)
(2. 3. 6)
мұндағы
 - тор қадамының өлшемі,
- тор қадамының өлшемі,
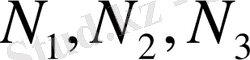 -
-
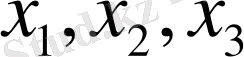 бағыттарына сәйкес тордың ұяшықтар саны.
бағыттарына сәйкес тордың ұяшықтар саны.
Есептелетін алгоритмде таралымды тор қолданылады, яғни торлы функцияның координаттары кеңістікте таратылған, оны 1 суреттен көруге болады.
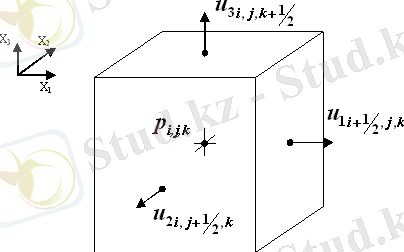
1 сурет. Торлық шаблон
Бұл бізге әрбір ұяшықты дене центріндегі есептелетін
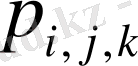 қысымы мен
қысымы мен
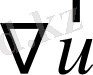 дивергенциясы көлемінің элементі ретінде интерпретациялауға мүмкіндік береді. Сонымен қатар шекарадағы жылдамдықтар векторының құраушысын білгеніміз осы шекара арқылы өтетін қозғалыс мөлшерінің ағынын есептеуге мүмкіндік береді.
дивергенциясы көлемінің элементі ретінде интерпретациялауға мүмкіндік береді. Сонымен қатар шекарадағы жылдамдықтар векторының құраушысын білгеніміз осы шекара арқылы өтетін қозғалыс мөлшерінің ағынын есептеуге мүмкіндік береді.
Таралымды тордың тағы бір артықшылығы қысым ұяшықтың центрінде есептелетіндіктен және тек үйлесімді торлар(
 шекарасымен жанасқан ұяшықтар) қарастырылып отырғандықтан осы ұяшықтардың қабырғасы
шекарасымен жанасқан ұяшықтар) қарастырылып отырғандықтан осы ұяшықтардың қабырғасы
 бөлігімен тура беттеседі, сондықтан есептеу кезінде
бөлігімен тура беттеседі, сондықтан есептеу кезінде
 -дағы қысымның шартын білудің қажеті жоқ.
-дағы қысымның шартын білудің қажеті жоқ.
Таралымды торды қолдану
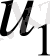 ,
,
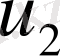 ,
,
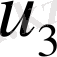 және
және
 мәндерін көршілес ұяшықтарда байланыстыруға және осцилляцияның пайда болуын болдырмауға мүмкіндік береді.
мәндерін көршілес ұяшықтарда байланыстыруға және осцилляцияның пайда болуын болдырмауға мүмкіндік береді.
- Теңдеудің жеке мүшелерінің аппроксимациясы
Жылдамдықтың көлденең құраушысы
u
1
үшін жазылған теңдеудің жеке мүшелерінің дискретизациясы
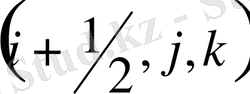 тордың нүктесіне сәйкес центрленген ақырлы айырымды өрнектер арқылы жүзеге асады.
тордың нүктесіне сәйкес центрленген ақырлы айырымды өрнектер арқылы жүзеге асады.
-Коньвективтік мүшелер:
Коньвективтік мүшелерді аппроксимациялау үшін жоғарғы ретті дәлдікпен жазылған туындылар(ағынға қарсы) қолданылады.
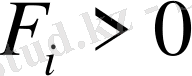 жағдайында:
жағдайында:
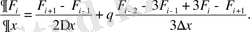 (2. 4. 1)
(2. 4. 1)
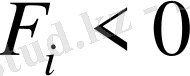 жағдайында:
жағдайында:
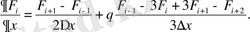 (2. 4. 2)
(2. 4. 2)
(2. 4. 1), (2. 4. 2) формулаларын қолданып келесі өрнекті аламыз:
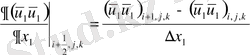
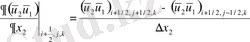
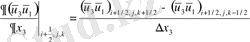
-Диффузиялық мүшелер:
Диффузиялық мүшелерді аппроксимациялау нәтижесінде келесі түрде болады:
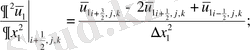

-Торлы мүшелер:
(2. 2. 2) -(2. 2. 3) теңдеулерге кіші масштабты турбуленттікті анықтайтын
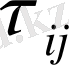 мүшелері кіреді. Бұл жұмыста Смагоринский торлы моделі қолданылады және аппроксимация нәтижесінде торлы мүшелер келесі түрде болады:
мүшелері кіреді. Бұл жұмыста Смагоринский торлы моделі қолданылады және аппроксимация нәтижесінде торлы мүшелер келесі түрде болады:
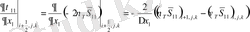
мұндағы

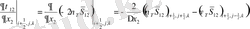
мұндағы

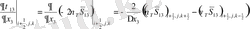
мұндағы

Жылдамдықтың көлденең құраушысы
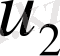 үшін жазылған теңдеудің жеке мүшелерінің
үшін жазылған теңдеудің жеке мүшелерінің
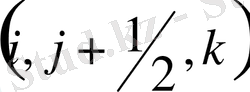 нүктесіндегі аппроксимациясын қарастырайық.
нүктесіндегі аппроксимациясын қарастырайық.
-Конвективті мүшелер:
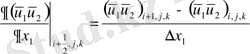
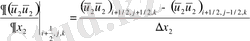
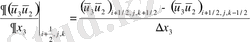
-Диффузиялық мүшелер:


-Торлы мүшелер:
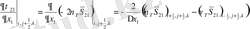
мұндағы

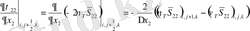
мұндағы

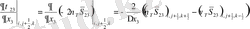
мұндағы

Жылдамдықтың тік құраушысы
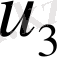 үшін жазылған теңдеудің жеке мүшелерінің
үшін жазылған теңдеудің жеке мүшелерінің
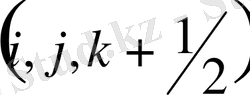 нүктесіндегі аппроксимациясын қарастырайық.
нүктесіндегі аппроксимациясын қарастырайық.
-Конвективті мүшелер:
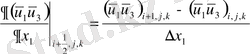
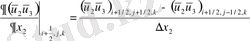
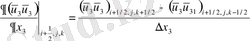
-Диффузиялық мүшелер:


-Торлы мүшелер:
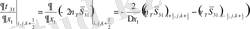
мұндағы
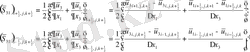
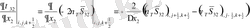
мұндағы


мұндағы

- Аралық жылдамдықтар өрісі
Аралық жылдамдықтар өрісі бөлшектік қадам әдісімен табылады. Бөлшектік қадам әдісінің әрбір сатысындағы жылдамдықты беснүктелік қуалау әдісімен шешіледі.
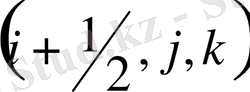 нүктесіндегі жылдамдықтың көлденең құраушысы
нүктесіндегі жылдамдықтың көлденең құраушысы
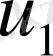 үшін бөлшектік қадам әдісін қарастырайық.
үшін бөлшектік қадам әдісін қарастырайық.
Бірінші этапта
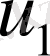 жылдамдығы
жылдамдығы
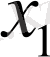 координатасының бағыты бойынша ізделінеді:
координатасының бағыты бойынша ізделінеді:
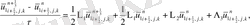
(2. 3. 5) операторлардың берілуін және жеке мүшелерінің аппроксимацияларын қолданып ұқсас қосылғыштарды келтірейік:

мұндағы
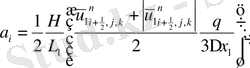
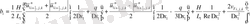
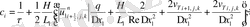

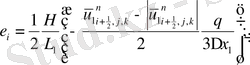
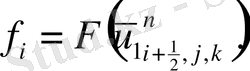
Келтірілген теңдеулер беснүктелік қуалау әдісімен шешіліп
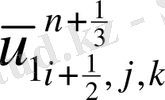 мүшесі табылады.
мүшесі табылады.
Екінші этапта
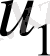 жылдамдығы
жылдамдығы
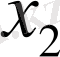 координатасының бағыты бойынша ізделінеді:
координатасының бағыты бойынша ізделінеді:
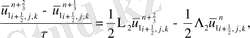
ұқсас қосылғыштарды келтірейік:

мұндағы
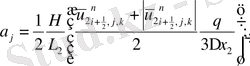

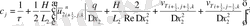

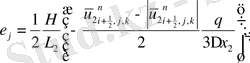
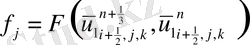
Келтірілген теңдеулер беснүктелік қуалау әдісімен шешіліп
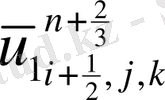 мүшесі табылады.
мүшесі табылады.
Үшінші этапта
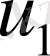 жылдамдығы
жылдамдығы
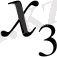 координатасының бағыты бойынша ізделінеді:
координатасының бағыты бойынша ізделінеді:
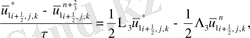
ұқсас қосылғыштарды келтірейік:

мұндағы
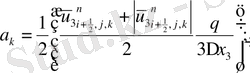

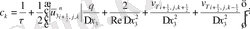

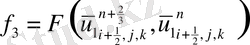
Келтірілген теңдеулер беснүктелік қуалау әдісімен шешіліп
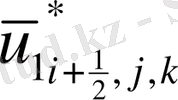 мүшесі табылады.
мүшесі табылады.
Енді
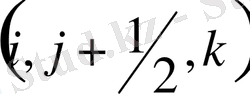 нүктесіндегі жылдамдықтың көлденең құраушысы
нүктесіндегі жылдамдықтың көлденең құраушысы
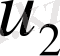 үшін бөлшектік қадам әдісін қарастырайық.
үшін бөлшектік қадам әдісін қарастырайық.
Бірінші этапта
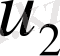 жылдамдығы
жылдамдығы
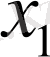 координатасының бағыты бойынша ізделінеді:
координатасының бағыты бойынша ізделінеді:
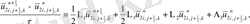
(2. 3. 5) операторлардың берілуін және жеке мүшелерінің аппроксимацияларын қолданып ұқсас қосылғыштарды келтірейік:

мұндағы
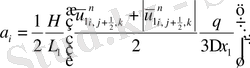

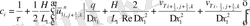

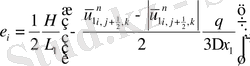
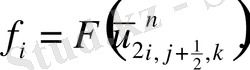
Келтірілген теңдеулер беснүктелік қуалау әдісімен шешіліп
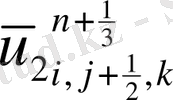 мүшесі табылады.
мүшесі табылады.
Екінші этапта
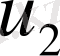 жылдамдығы
жылдамдығы
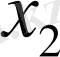 координатасының бағыты бойынша ізделінеді:
координатасының бағыты бойынша ізделінеді:
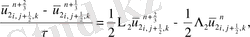
ұқсас қосылғыштарды келтірейік:

мұндағы
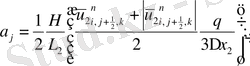
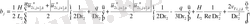
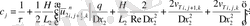
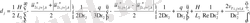
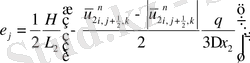
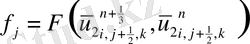
Келтірілген теңдеулер беснүктелік қуалау әдісімен шешіліп
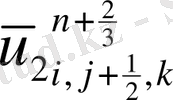 мүшесі табылады.
мүшесі табылады.
Үшінші этапта
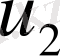 жылдамдығы
жылдамдығы
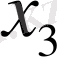 координатасының бағыты бойынша ізделінеді:
координатасының бағыты бойынша ізделінеді:
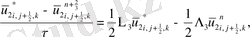
ұқсас қосылғыштарды келтірейік:

мұндағы
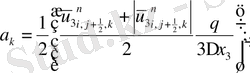
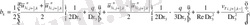
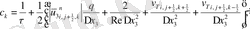

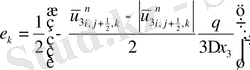
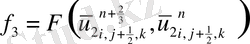
Келтірілген теңдеулер беснүктелік қуалау әдісімен шешіліп
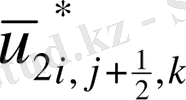 мүшесі табылады.
мүшесі табылады.
Енді
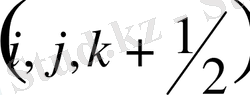 нүктесіндегі жылдамдықтың тік құраушысы
нүктесіндегі жылдамдықтың тік құраушысы
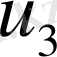 үшін бөлшектік қадам әдісін қарастырайық.
үшін бөлшектік қадам әдісін қарастырайық.
Бірінші этапта
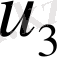 жылдамдығы
жылдамдығы
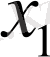 координатасының бағыты бойынша ізделінеді:
координатасының бағыты бойынша ізделінеді:
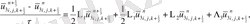
(2. 3. 5) операторлардың берілуін және жеке мүшелерінің аппроксимацияларын қолданып ұқсас қосылғыштарды келтірейік:

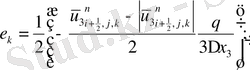
мұндағы
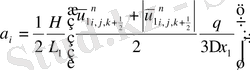
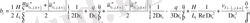
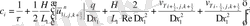

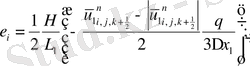
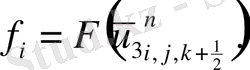
Келтірілген теңдеулер беснүктелік қуалау әдісімен шешіліп
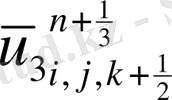 мүшесі табылады.
мүшесі табылады.
Екінші этапта
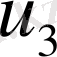 жылдамдығы
жылдамдығы
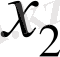 координатасының бағыты бойынша ізделінеді:
координатасының бағыты бойынша ізделінеді:
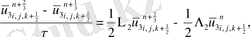
ұқсас қосылғыштарды келтірейік:
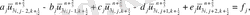
мұндағы


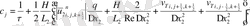

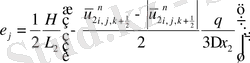
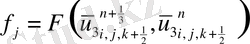
Келтірілген теңдеулер беснүктелік қуалау әдісімен шешіліп
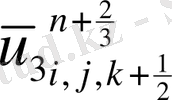 мүшесі табылады.
мүшесі табылады.
Үшінші этапта
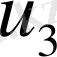 жылдамдығы
жылдамдығы
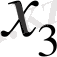 координатасының бағыты бойынша ізделінеді:
координатасының бағыты бойынша ізделінеді:
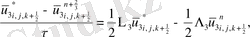
ұқсас қосылғыштарды келтірейік:

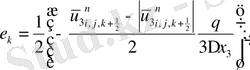
мұндағы
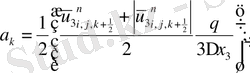

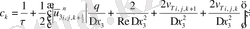

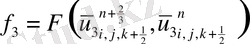
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz